Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Investigaciones Biomédicas
versión impresa ISSN 0864-0300
Rev Cubana Invest Bioméd vol.31 no.3 Ciudad de la Habana jul.-sep. 2012
ACTUALIZACIÓN
Modelos computacionales del comportamiento del cartílago articular
Computational models of articular cartilage behavior
Ing. Oscar Rodrigo López-VacaI, MSc. Carlos Alberto Narváez-TovarI, Ing. Diego Alexander Garzón-AlvaradoII
IFacultad de Ingeniería Mecánica, Universidad Santo Tomás. Bogotá, Colombia.
IIDepartamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia. Bogotá, Colombia.
RESUMEN
El cartílago articular suministra a las articulaciones diartrodiales baja fricción, resistencia al desgaste en las superficies de contacto y distribuye los esfuerzos en las zonas donde se presenta contacto con el hueso; adicionalmente, es un tejido alinfático y avascular, razón por la cual su regeneración toma demasiado tiempo y en pacientes con avanzada edad no es posible realizarla. Con el propósito de estudiar y entender completamente el comportamiento del cartílago bajo diferentes condiciones de carga y en presencia de enfermedades como la osteoartritis, se han creado diferentes modelos computacionales que incluyen características propias de la estructura del tejido cartilaginoso que permiten predecir su comportamiento en condiciones normales y anormales, disminuyendo tiempos y costos de experimentación. Este artículo de actualización expone las principales características estructurales y biológicas del cartílago articular y presenta diferentes modelos computacionales que permiten modelar el tejido cartilaginoso de acuerdo con sus principales características y de esta forma simular el deterioro del cartílago bajo diferentes condiciones y enfermedades.
Palabras clave: cartílago articular, materiales bifásicos, mecanobiología, modelos computacionales.
ABSTRACT
The articular cartilage provides diarthrodial articulations with low friction, resistance to wear on contact surfaces, and an effective distribution of efforts in areas of contact with the bone. On the other hand, because their tissue is alymphatic and avascular, regeneration takes a long time and is not possible in elderly patients. Various computational models have been developed to study and fully understand cartilage behavior under varying load conditions and in the presence of diseases such as osteoarthritis. The models include specific features of cartilaginous tissue allowing to predict its behavior in normal and abnormal conditions, reducing experimentation time and costs. This update paper presents the main structural and biological characteristics of the articular cartilage, as well as various computational models representing cartilaginous tissue according to its main features, with a view to simulating cartilage deterioration under varying conditions and diseases.
Key words: articular cartilage, biphasic materials, mechanobiology, computational models.
INTRODUCCIÓN
Desde el punto de vista de la biomecánica y la mecanobiología un modelo es una interpretación matemática del comportamiento mecánico y biológico de un cuerpo material o sistema. Estos tipos de modelos son frecuentemente llamados modelos mecánicos debido a que se basan en leyes físicas o relaciones empíricas las cuales son relevantes para la consideración de diversas variables del problema. En los modelos mecanobiológicos además de las leyes físicas se intenta determinar de forma cuantitativa la influencia del entorno mecánico en la diferenciación de tejidos, así como en su crecimiento, adaptación y modificación estructural incorporando los procesos biológicos y celulares implicados.1 El papel de los modelos mecánicos y mecanobiológicos es esclarecer la importancia de los diferentes factores que intervienen en los procesos mecánicos y biológicos para luego simularlos y predecir la respuesta de un sistema mecánico o mecanobiológicos. También estos modelos pueden ayudar al diseño de sistemas o procesos y pueden servir como herramienta de acompañamiento experimental o investigaciones clínicas. Para condiciones simples los modelos pueden ser formulados utilizando aproximaciones analíticas. Sin embargo, en el análisis de problemas más complejos se deben emplear métodos numéricos o computacionales. Estos modelos computacionales necesitan de un desarrollo significativo de software y un uso considerable de herramientas y sistemas de cómputo. Actualmente los modelos computacionales complejos para sistemas o procesos biológicos asumen la integración de disciplinas fundamentales (física, biología, química) con métodos numéricos, ciencias computacionales y medicina.2
El tejido cartilaginoso es un tejido que, por sus características mecánicas y biológicas, ha llamado la atención de muchos investigadores y ha sido objeto de la creación de diferentes modelos biomecánicos3 y mecanobiológicos4 para caracterizar completamente su comportamiento. El cartílago es la principal parte de las articulaciones asociada con la protección del hueso por impacto, contacto y fricción entre los huesos mientras se produce un movimiento. El cartílago es un material multifásico, no lineal, viscoelástico y permeable, consiste en dos fases principales, una sólida y una líquida. La fase sólida está compuesta principalmente de fibras entrecruzadas de colágeno, proteoglicanos, glicoproteínas y condrocitos en forma agregada. La fase fluida está compuesta principalmente por agua en un 78 % en peso del cartílago. Dentro de la fase sólida se puede reconocer los condrocitos (2 % en peso) y la matriz extracelular (20 % en peso).5-8 El cartílago es clasificado como un material elástico, fibrocartilaginoso o hialino el cual depende de su composición molecular.8 El oído y la laringe están compuestos de cartílago elástico, mientras que el fibrocartílago está asociado con las articulaciones de la rodilla y los discos intervertebrales. El cartílago hialino es la forma más predominante del cartílago y es la más comúnmente asociada al sistema óseo.6
Este artículo recoge los diferentes modelos computacionales desarrollados con el objeto de describir, incluyendo la mayor cantidad de características asociadas, el comportamiento del cartílago articular. Para la selección apropiada del tipo de modelo a utilizar, se requiere del conocimiento de las propiedades mecánicas de este tejido que por su arquitectura puede ser modelado desde su forma básica incluyendo solo aspectos biomecánicos, así como aquellos aspectos biológicos y celulares que hacen más complejos los modelos a utilizar. Es por esto que este artículo comienza por hacer una revisión de las principales características mecánicas y biológicas del cartílago articular, para luego describir los diferentes modelos computacionales disponibles.
MODELOS COMPUTACIONALES ANALÍTICOS DEL COMPORTAMIENTO DEL CARTÍLAGO ARTICULAR
A. Modelos bifásicos
Para describir el comportamiento del CA son frecuentemente usados y aceptados los modelos bifásicos. En estos modelos9,10 el tejido se asume como una matriz sólida incompresible, hidratada con un fluido de igual forma incompresible. Por lo tanto los esfuerzos totales en el tejido están dados por la suma de los esfuerzos del material sólido y del fluido.11
![]()
donde ![]() es el tensor de esfuerzos efectivo, p es la presión hidrostática del fluido, e I es un tensor unitario. En muchos modelos bifásicos la matriz sólida es asumida como lineal, elástica e isotrópica, así el tensor de esfuerzos efectivo está dado por:
es el tensor de esfuerzos efectivo, p es la presión hidrostática del fluido, e I es un tensor unitario. En muchos modelos bifásicos la matriz sólida es asumida como lineal, elástica e isotrópica, así el tensor de esfuerzos efectivo está dado por:
![]()
donde e representa la dilatación, e es el tensor de deformaciones y l y µ representan las constantes de Lamé, las cuales son función del módulo de Young E y la relación de Poisson v, como
![]()
![]()
en ausencia de intercambio de masa, la variación de la masa total debe ser igual a la cantidad de flujo de fluido a través de la superficie del tejido. Por lo tanto, la ley de conservación de masa es dada por Huyghe12
![]()
donde ![]() es la fracción de fluido y
es la fracción de fluido y ![]() y
y ![]() son las velocidades de las fases sólida y fluida respectivamente. De acuerdo con la ley de Darcy el flujo de fluido está relacionado con la presión del fluido hidrostático como
son las velocidades de las fases sólida y fluida respectivamente. De acuerdo con la ley de Darcy el flujo de fluido está relacionado con la presión del fluido hidrostático como
![]()
En esta ecuación el término de la izquierda representa el flujo de fluido a través de la superficie de la mezcla y k es la permeabilidad. Con la ecuación 6 la ley de conservación de masa de la ecuación 5 quedaría
![]()
las propiedades en el material del CA son fuertemente dependientes de la profundidad, en muchos modelos bifásicos esta dependencia a la profundidad ha sido incluida usando un módulo agregado dependiente de la profundidad o permeabilidad. Los modelos isotrópicos bifásicos han sido utilizados para analizar experimentos de carga como ensayos de compresión confinada y sin confinar, ensayos de dureza (indentación) e impacto, estos aplicados tanto en cartílago sano y como en cartílagos con efectos de la OA. Aunque los modelos bifásicos lineales incluyen la viscoelasticidad del CA dependiente del flujo del fluido, no incluyen características importantes como permeabilidad dependiente de la deformación, anisotropía causada por las redes de colágeno, viscoelasticidad independiente del flujo y comportamiento a la inflamación; a continuación se describen algunos de estos modelos.
B. Permeabilidad dependiente de la deformación
La permeabilidad del cartílago es dependiente de la deformación y puede ser descrita por:
![]()
donde ![]() y M son constantes del material y
y M son constantes del material y![]() es la dilatación de la matriz sólida. En términos de la relación de vacíos
es la dilatación de la matriz sólida. En términos de la relación de vacíos ![]() la ecuación 8 puede ser escrita según lo hicieron Li y otros13
la ecuación 8 puede ser escrita según lo hicieron Li y otros13

donde e y ![]() son las relaciones de vacíos actual e inicial respectivamente.
son las relaciones de vacíos actual e inicial respectivamente.
C. Anisotropía
La composición y la estructura del cartílago varían a través de la profundidad del tejido. Por lo tanto, las propiedades mecánicas del CA son no homogéneas y anisotrópicas. Debido a la distribución no homogénea de los PGs, hay una no homogeneidad en la distribución de la FCD a través de la profundidad del tejido.14-16
Como la orientación de las fibras de colágeno cambia sobre la altura del tejido, y debido a que solo puede resistir cargas de tensión, la red de colágeno juega un importante papel en la falta de homogeneidad mecánica y en la anisotropía del CA. En la zona superficial las fibras de colágeno están ubicadas en un arreglo paralelo a la superficie articular, de este modo dan a esta capa una alta resistencia a la tensión en esta dirección,17 mientras que estas tienen una baja resistencia en la dirección perpendicular. Estas fibras, por lo tanto, contribuyen de manera significativa a la resistencia mecánica contra la indentación y casi no ofrecen ninguna resistencia a la inflamación. Las fibras en las zonas profundas son principalmente orientadas perpendiculares a la superficie articular y por lo tanto no suministran gran resistencia contra la inflamación. Debido a la compleja red de colágeno el CA es altamente anisotrópico y tiene diferentes propiedades en tensión y en compresión. En la literatura muchos modelos han sido encontrados e incluyen estas características; a continuación se describen los modelos más usados.
1) Modelos transversalmente isotrópicos
En un material transversalmente isotrópico se asume que todas las fibras están dispuestas en la misma dirección. Por lo tanto un material transversalmente isotrópico puede ser visto como un material ortotrópico con un plano de isotropía La dirección paralela de las fibras es llamada dirección longitudinal y las direcciones perpendiculares a las fibras son llamadas direcciones perpendiculares. Cuando se asumen fibras en una tercera dirección, los esfuerzos en el sólido18 están dados por:
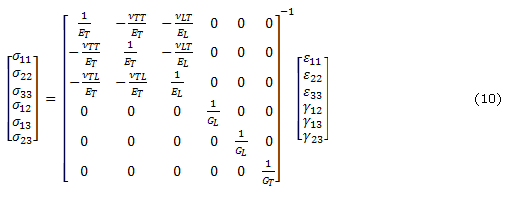
donde ![]() y
y ![]() hacen referencia la módulo de Young en las direcciones longitudinal y transversal respectivamente,
hacen referencia la módulo de Young en las direcciones longitudinal y transversal respectivamente, ![]() es el módulo a cortante en la dirección longitudinal y
es el módulo a cortante en la dirección longitudinal y ![]() ,
, ![]() y
y ![]() son las relaciones de Poisson que dan la deformación en las direcciones longitudinal (a lo largo de las fibras) o transversal (perpendicular a las fibras) para un estiramiento en la otra dirección. El módulo a cortante transversal
son las relaciones de Poisson que dan la deformación en las direcciones longitudinal (a lo largo de las fibras) o transversal (perpendicular a las fibras) para un estiramiento en la otra dirección. El módulo a cortante transversal![]() está dado por
está dado por
![]()
debido a la simetría
![]()
2) Modelos de fibras reforzadas
Estos modelos se utilizan para incluir no linealidades en un estado de compresión tensión de la matriz sólida. En un modelo reforzado con fibras13,1923 la red fibrosa (red de colágeno) contribuye a la rigidez mecánica del material, además de la matriz isotrópica. Los esfuerzos sólidos del material reforzado con fibras están dados por la suma de los esfuerzos de la matriz y las fibras. Actualmente se conocen dos tipos de modelos de fibras reforzadas, modelos de resortes y modelos continuos. En los modelos de resortes las fibras son representadas por resortes entre los nodos de los elementos, por lo tanto, las fibras solo pueden ser representadas en la dirección de los elementos. El esfuerzo sólido de un material reforzado con fibras está dado por la suma de los esfuerzos presentes en la matriz y en las fibras, como
![]()
donde ![]() y
y ![]() representan los esfuerzos normales en la dirección i, en la matriz y en las fibras de colágeno respectivamente. Li y otros13,20 han realizado modelos reforzados con fibras más sofisticados basados en resortes. En sus primeros modelos la rigidez de las fibras de colágeno fue representada por un resorte lineal con rigidez
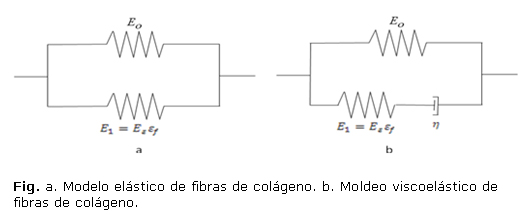
representan los esfuerzos normales en la dirección i, en la matriz y en las fibras de colágeno respectivamente. Li y otros13,20 han realizado modelos reforzados con fibras más sofisticados basados en resortes. En sus primeros modelos la rigidez de las fibras de colágeno fue representada por un resorte lineal con rigidez ![]() , en paralelo con un resorte no lineal con rigidez
, en paralelo con un resorte no lineal con rigidez ![]() (Fig. a), donde
(Fig. a), donde ![]() es la deformación en la dirección de la fibra. El esfuerzo fibril
es la deformación en la dirección de la fibra. El esfuerzo fibril ![]() en este modelo está dado por:
en este modelo está dado por:
![]()
En sus trabajos más recientes24 las fibras fueron modeladas como viscoelásticas de forma tal que el esfuerzo fibril está dado por
![]()
donde la función de relajación es representada por un espectro de aproximación como
![]()
siendo ![]() como la característica de tiempo para la disipación viscoelástica.
como la característica de tiempo para la disipación viscoelástica.
En los modelos continuos de fibras reforzadas la orientación de las fibras es independiente de la malla. Por lo tanto, pueden ir en cualquier dirección lo cual permite tener una representación geométrica realista de la red de colágeno. En estos modelos el esfuerzo sólido está dado por
![]()
donde ![]() son los esfuerzos en la i-ésima fibra y
son los esfuerzos en la i-ésima fibra y ![]() las direcciones actuales en las fibras de la i-ésima fibra.
las direcciones actuales en las fibras de la i-ésima fibra.
En los modelos de Wilson y otros19,25 las fibras de colágeno que son asumidas como viscoelásticas son representadas por un resorte lineal con rigidez ![]() , en paralelo con un resorte no lineal con rigidez
, en paralelo con un resorte no lineal con rigidez ![]() en serie con un amortiguador lineal con constante de amortiguamiento h (fig. b). Asumiendo que las fibras solo resisten tensión los esfuerzos en las fibras viscoelásticas están dados por
en serie con un amortiguador lineal con constante de amortiguamiento h (fig. b). Asumiendo que las fibras solo resisten tensión los esfuerzos en las fibras viscoelásticas están dados por
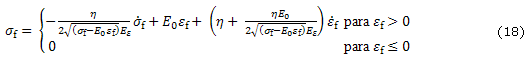
La diferencia más significativa entre el modelo de fibras reforzadas basadas en resortes y el modelo transversalmente isotrópico es que la primera resiste solo tensión mientras que en el segundo modelo se contempla la misma rigidez tanto en tensión como en compresión. La principal característica de este modelo es que son incluidas las propiedades no lineales de las fibras. Una ventaja adicional del modelo continuo reforzado con fibras es que las fibras pueden estar orientadas en cualquier dirección.
Los modelos bifásicos reforzados con fibras basados en resortes han sido aplicados en compresión sin confinamiento, principalmente para la caracterización de la red de colágeno en la respuesta del cartílago dependiendo del tiempo.
D. Viscoelasticidad independiente del flujo (Modelos viscoporoeslásticos)
El CA es altamente viscoelástico, hay dos mecanismos responsables de este comportamiento:6,22
(a) la fuerza de arrastre por fricción del flujo a través de la matriz sólida porosa, (i.e. mecanismo dependiente del flujo), y
(b) la deformabilidad en función del tiempo de la matriz sólida (i.e. mecanismo independiente del flujo).
En la matriz extracelular tanto las fibras de colágeno como el gel de PG en los cuales están embebidos presentan viscolelasticidad independiente del flujo.
Debido a la exudación de fluidos del tejido cuando el cartílago está bajo cargas mecánicas, ocurre una pérdida en su volumen. En equilibrio, no hay flujo de fluido o gradientes de presión, y la carga completa es asumida por la matriz sólida y las presiones de inflamación interna. Una vez removida la carga o la deformación, el CA retornará a sus dimensiones iníciales, debido a la elasticidad de la matriz sólida y al incremento de la presión osmótica dentro del tejido.
El movimiento del fluido en el cartílago es gobernado por la permeabilidad hidráulica de la matriz sólida. Debido a que la permeabilidad de la matriz extracelular es relativamente baja, es difícil para el fluido intersticial escapar del tejido bajo carga mecánica.2629 Por lo tanto, se puede demostrar que la carga negativa de la FCD de los PGs limita el flujo de fluido, y de este modo afecta la permeabilidad del tejido.6,27 La permeabilidad es también altamente dependiente de los tamaños de los poros en la matriz extracelular.29 Cuando el tejido es deformado la FCD y el tamaño de los poros cambian, así la permeabilidad del cartílago está en función de las deformaciones.
El comportamiento dependiente del tiempo del CA es causado por efectos viscoelásticos dependientes e independientes del flujo de fluido, estas características generalmente son incluidas en los modelos viscoporoelásticos. Se conocen en la literatura dos modelos viscoporoelásticos, en el primero, la matriz sólida es solo viscoelástica en cortante30 y en el segundo la matriz sólida es viscoelástica tanto en cortante como en deformación volumétrica. El esfuerzo sólido en estos modelos está dado por:
![]()
y
![]()
respectivamente. Aquí t es una constante de relajación de tiempo y e la componente deviatórica del tensor elástico de deformació![]() n. La función de relajación
n. La función de relajación ![]() está por
está por
![]()
donde el espectro de relajación continua está dado por

Donde ![]() y
y ![]() son las constantes de relajación de corto y largo plazo, respectivamente, y c es la magnitud del espectro de potencia de relajación. Además de los parámetros para un material bifásico en el caso isotrópico, el modelo viscoporoelástico adiciona tres parámetros, los cuales son: un espectro de valor discreto c, una constante de relajación de corto plazo
son las constantes de relajación de corto y largo plazo, respectivamente, y c es la magnitud del espectro de potencia de relajación. Además de los parámetros para un material bifásico en el caso isotrópico, el modelo viscoporoelástico adiciona tres parámetros, los cuales son: un espectro de valor discreto c, una constante de relajación de corto plazo ![]() y una constante de relajación de largo plazo.
y una constante de relajación de largo plazo.
E. Presión osmótica
1) Modelo mecanoelectroquímico
Los modelos realizados incluyen la influencia de la concentración iónica y flujo iónico y, por lo tanto, permiten la representación del comportamiento de inflamación del CA derivando una pequeña deformación de extensión mecano-electroquímica del modelo bifásico que incluye tres fases: una fase sólida incompresible, una fase fluida incompresible y una fase iónica monovalente, así se conocen estos modelos como trifásicos o tetrafásicos.
El esfuerzo total para este caso es el mismo usado para el modelo bifásico (ecuación 1) pero en este caso la presión hidrostática31 está dada por:
![]()
donde ![]() es el potencial electroquímico y
es el potencial electroquímico y ![]() el gradiente de presión osmótico, en ausencia de intercambio de masa la ley de conservación de masa está dada por:
el gradiente de presión osmótico, en ausencia de intercambio de masa la ley de conservación de masa está dada por:
![]()
donde ![]() y
y ![]() son la fracción de volumen y la componente a de la velocidad, respectivamente. La relación entre la permeabilidad y la difusión-convección iónica y la componente de la velocidad a se describe como:
son la fracción de volumen y la componente a de la velocidad, respectivamente. La relación entre la permeabilidad y la difusión-convección iónica y la componente de la velocidad a se describe como:
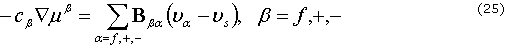
donde ![]() es la concentración molecular de la fase b por unidad de volumen de mezcla,
es la concentración molecular de la fase b por unidad de volumen de mezcla, ![]() es el potencial molecular y
es el potencial molecular y ![]() es una matriz simétrica de coeficientes friccionales. El gradiente de presión osmótica de la ecuación 23 está dado por
es una matriz simétrica de coeficientes friccionales. El gradiente de presión osmótica de la ecuación 23 está dado por
![]()
donde la presión osmótica interna y externa están dadas por:

respectivamente. Donde R es la constante de los gases y T la temperatura absoluta, ![]() y
y ![]() son las concentraciones de los cationes móviles (Na+) y los aniones (Cl-), respectivamente,
son las concentraciones de los cationes móviles (Na+) y los aniones (Cl-), respectivamente, ![]() y
y ![]() representan los coeficientes osmóticos internos y externos. La electroneutralidad debe mantenerse en cada punto del tejido así:
representan los coeficientes osmóticos internos y externos. La electroneutralidad debe mantenerse en cada punto del tejido así:
![]()
donde ![]() es la FCD. El potencial químico por mol de NaCl en la solución externa
es la FCD. El potencial químico por mol de NaCl en la solución externa ![]() y la que está en el tejido m están dados por:
y la que está en el tejido m están dados por:
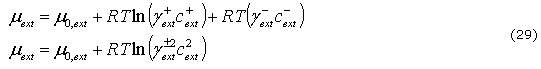

donde ![]() y
y ![]() son los coeficientes de actividad principal y
son los coeficientes de actividad principal y ![]() el potencial de concentración independiente.
el potencial de concentración independiente.
Las concentraciones de equilibrio interno de iones están dadas por

La presión osmótica interna en equilibrio16 está dada por:

Los modelos mecanoelectroquímicos han sido utilizados para describir el comportamiento de inflamación del cartílago articular.
CONCLUSIONES
En la caracterización del cartílago articular y de su comportamiento se hace uso de la ayuda de los diferentes modelos mencionados en este artículo y utilizando el método de los elementos finitos como herramienta de análisis, consideramos que, además de la determinación de esfuerzos y deformaciones en los diferentes componentes del CA, estos modelos pueden llegar a ser una herramienta útil en el estudio y desarrollo de modelos relacionados con el daño del tejido hialino por condiciones de desgaste del cartílago, así como, el entendimiento del comportamiento mecánico en su regeneración y en su degeneración por envejecimiento o por enfermedades como la osteoartritis.
REFERENCIAS BIBLIOGRÁFICAS
1. Doblaré M. Sobre el modelado en biomecánica y mecanobiología. Discurso de posesión de la Real Academia de Ciencias Físicas y Exactas de Zaragoza. 2005. p. 1-30.
2. Garzón-Alvarado DA, Duque Daza CA, Ramírez AM. Sobre la aparición de la biomecánica y la mecanobiología computacional: experimentos computacionales y recientes hallazgos. Rev Cubana Invest Bioméd. 2009;28(3):83-101.
3. Boschetti F, Pennati G, Gervaso F, Peretti GM, Dubini G. Biomechanical properties of human articular cartilage under compressive loads. Biorheology. 2004;41(3-4):159-66.
4. Carter DR, Wong M. Modelling cartilage mechanobiology. Philosophical transactions of the Royal Society of London. Series B. Biological sciences. 2003;358(1437):1461-7.
5. Ulrich W, Meyer PH. Bone and Cartilage Engineering. Berlin-Germany: Springer; 2006. p. 55.
6. Flik KR, Verma N, Cole BJ. Cartilage Repair Strategies. (Williams RJ, ed.). Totowa, New Jersey: Humana Press; 2007:1-12.
7. Shieh AC, Athanasiou K Principles of Cell Mechanics for Cartilage Tissue Engineering. Annals of Biomedical Engineering. 2003;31(1):1-11.
8. Kheir E, Shaw D. Hyaline articular cartilage. Orthopaedics and Trauma. 2009;23(6):450-55.
9. García JJ, Cortés DH. Modelo bifaìsico no-lineal de elementos finitos para el anaìlisis mecaìnico de tejidos bioloìgicos. Parte I- Formulacioìn teoìrica. Ingeniería y Desarrollo. 2006;19:44-56.
10. García JJ, Cortés DH. Modelo bifásico no-lineal de elementos finitos para el análisis mecánico de tejidos biológicos Parte II: Implementación numérica y validación. Ingeniería y Desarrollo. 2006;19:57-73.
11. Landinez NS, Vanegas JC, Garzón DA. Modelado Matemático del Comportamiento de un Fragmento de cartílago articular. Dyna. 2009;76(157):133-44.
12. Huyghe J. Quadriphasic mechanics of swelling incompressible porous media. International Journal of Engineering Science. 1997;35(8):793-80.
13. Li L, Soulhat J, Buschmann MD, Shirazi-Adl A. Nonlinear Analysis of Cartilage in Unconfined Ramp Compression Using a Fibril Reinforced Poroelastic Model. Clinical Biomechanics. 1999;14:673-682.
14. Boschetti F, Pennati G, Scienza F. Depth Dependent Creep Response of Human Articular Cartilage During Compression. Experimental Testing and Simulation. In: Summer Bioengineering Conference. Florida; 2003:1139-42.
15. Chen SS, Falcovitz YH, Schneiderman R, Maroudas SR. Depth-dependent compressive properties of normal aged human femoral head articular cartilage: relationship to fixed charge density. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2001;9(6):561-9.
16. Korhonen RK, Herzog W. Depth-dependent analysis of the role of collagen fibrils, fixed charges and fluid in the pericellular matrix of articular cartilage on chondrocyte mechanics. Journal of biomechanics. 2008;41(2):480-5.
17. Wachtel E, Maroudas SR. Age-related changes in collagen packing of human articular cartilage. Biochimica et biophysica acta. 1995;1243(2):239-43.
18. Kowalczyk P. Elastic properties of cancellous bone derived from finite element models of parameterized microstructure cells. Journal of biomechanics. 2003;36(7):961-72.
19. Wilson W, Van Donkelaar CC, Van Rietbergen B, Huiskes R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. Journal of biomechanics. 2005;38(6):1195-204.
20. Li LP, Buschmann MD. A fibril reinforced nonhomogeneous poroelastic model for articular cartilage: inhomogeneous response in unconfined compression. Biomechanics. 2000;33:1533-41.
21. Shirazi R, Shirazi-Adl, Hurtig M. Role of cartilage collagen fibrils networks in knee joint biomechanics under compression. Journal of biomechanics. 2008;41(16):3340-8.
22. Li LP, Herzog W. The role of viscoelasticity of collagen fibers in articular cartilage: theory and numerical formulation. Biorheology. 2004;41(3-4):181-94.
23. Wilson W, Huyghe JM, Van Donkelaar CC. A composition-based cartilage model for the assessment of compositional changes during cartilage damage and adaptation. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2006;14(6):554-60.
24. Li LP, Herzog W. Strain-rate dependence of cartilage stiffness in unconfined compression: the role of fibril reinforcement versus tissue volume change in fluid pressurization. Journal of biomechanics. 2004;37:375-82.
25. Julkunen P, Kiviranta P, Wilson W, Jurvelin JS, Korhonen RK. Characterization of articular cartilage by combining microscopic analysis with a fibril-reinforced finite-element model. Journal of biomechanics. 2007;40(8):1862-70.
26. Mansoor H, Schugart RC. A numerical method for the continuous spectrum biphasic poroviscoelastic model of articular cartilage. Journal of biomechanics. 2006;39:177-183.
27. Ateshian G The role of interstitial fluid pressurization in articular cartilage lubrication. Journal of biomechanics. 2009;42(9):1163-76.
28. Soltz M Ateshian G. Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. Journal of biomechanics. 1998;31(10):927-34.
29. Basalo IM, Mauck RL, Kelly TA, Nicoll SB, Chen FH, Hung CT, et al. Cartilage interstitial fluid load support in unconfined compression following enzymatic digestion. Journal of biomechanical engineering. 2004;126(6):779-86.
30. DiSilvestro MR, Suh JK. A cross-validation of the biphasic poroviscoelastic model of articular cartilage in unconfined compression, indentation, and confined compression. Journal of biomechanics. 2001;34(4):519-25.
31. Kojic M, Filipovic N, Stojanovic B. Computer Modeling in Bioengineering. Londres: John Wiley & Sons, Ltd; 2008. p. 313-23.
Recibido: 5 de septiembre de 2011.
Aprobado: 25 de septiembre de 2011.
Oscar Rodrigo López-Vaca. Facultad de Ingeniería Mecánica, Universidad Santo Tomás. Bogotá, Colombia. Correo electrónico: orlopezv@unal.edu.co