REVISIÓN

 

Metodología de los gráficos de unión (bond graphs) en aplicaciones biomédicas

 

Bond graph methodology in biomedical applications

 

 

Ing. Diego Edgardo Fuentes Herrera, Ing. Diego Alexander Garzón-Alvarado

Departamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia. Bogotá, Colombia.

 

 

---

RESUMEN

Se presentan las aplicaciones realizadas en el campo de la medicina y la biología usando la técnica gráfica de modelado conocida como gráficos de unión (bond graphs), con el objetivo de mostrar las diferentes formas en las que se han usado los gráficos de unión como herramienta para la obtención de modelos y simulaciones de sistemas biológicos. Para el análisis de los trabajos realizados por los investigadores se hace una clasificación de los campos de aplicación con el fin de tener una visión más clara de lo diversa que ha sido la adaptación de esta metodología. Asimismo se discuten las posibilidades aún no exploradas, es decir, se habla de la aplicabilidad de los gráficos de unión en campos adicionales a los tratados en las referencias.

Palabras clave: modelado, gráficos de unión, biomédica.

---

ABSTRACT

The paper presents applications carried out in the field of medicine and biology using the graphical modeling technique known as bond graphs, with the purpose of showing the different ways in which bond graphs have been used to obtain models and simulations of biological systems. To approach the work done by researchers, a classification is made of the fields of application, so as to obtain a clearer view of the variety of adaptations undergone by the methodology. Possibilities not yet explored are also discussed, i.e. comments are included on the applicability of bond graphs to fields other than those mentioned in the references.

Key words: modeling, bond graphs, biomedicine.

---

 

 

INTRODUCCIÓN

La aplicación del saber de ciencias exactas como la física y las matemáticas en conjunción con los principios y técnicas de la ingeniería, en la formulación de modelos de sistemas dinámicos, ha contribuido considerablemente a la comprensión y análisis de los fenómenos que se producen en los organismos vivos. Específicamente en medicina, este conocimiento ha contribuido significativamente a la manera en que esta se enseña y aplica. En cuanto a lo primero, las simulaciones y representaciones gráficas de modelos y datos son una gran herramienta para la comprensión de los procesos fisiológicos, en una escala superior a la que se puede lograr con métodos tradicionales de enseñanza como libros o experimentos in vivo. De una simulación se pueden obtener visualizaciones gráficas y análisis de sensibilidad que contribuyen a: la construcción de modelos mentales, un mejor entendimiento de las relaciones entre las variables, la adquisición de habilidades en el diseño de experimentos, así como desarrollar destreza en el diagnóstico y el planteamiento de tratamientos.¹ Adicionalmente, un aspecto decisivo de los modelos de simulación en medicina, es la posibilidad de usarlos en situaciones en las que la experimentación no pueda ser realizada por cuestiones técnicas o éticas, o porque simplemente no es posible adquirir los datos pretendidos para el caso de estudio.²

Sin embargo, el modelado de fenómenos biológicos continuos en el tiempo es un proceso que requiere de conocimientos en diversas disciplinas por parte de quien formula el modelo pues, en general, cualquier sistema fisiológico involucra la coexistencia e interacción entre dos o más dominios energéticos (mecánico, eléctrico, hidráulico, químico, etc.). Además, es necesario dominar metodologías de modelado matemático, simulación (métodos numéricos y programación de computadores) y análisis estadístico de datos.³ Sin contar con que se debe tener un entendimiento profundo del fenómeno fisiológico analizado desde el punto de vista médico, en el caso de los seres humanos. Así pues, el creciente interés en el computador como herramienta de simulación en varias áreas, durante la segunda mitad del siglo XX, fomentó la tendencia del uso de modelos matemáticos para representar comportamientos fisiológicos con el fin de obtener datos cuantitativos del comportamiento de células, tejidos y órganos, a través de simulaciones de estos modelos, lo que da lugar al nacimiento de la fisiología computacional.^4,5

Diversas metodologías de modelado han sido utilizadas, siendo especialmente notables los modelos continuos representados a través de ecuaciones diferenciales ordinarias (EDO); también se encuentran modelos de sistemas en los que se considera la distribución de los parámetros y las variables en el espacio y en el tiempo, de manera que son empleadas ecuaciones diferenciales parciales (EDP). Adicionalmente, está muy extendido el análisis de los sistemas dinámicos, que son sistemas en los cuales su comportamiento como función del tiempo es importante.⁶ El estudio de estos últimos puede darse en el dominio de la frecuencia, del tiempo o en el espacio estado. Este espectro tan diverso es posible gracias a que se han formulado varios métodos de modelado, ya sea matemáticos (funciones de transferencia, ecuaciones de estado) o gráficos como diagramas de cuerpo libre, redes de circuitos, diagramas de bloques, diagramas de flujo, gráficos de unión; estos últimos son los menos difundidos y también los más prometedores en la investigación y desarrollo de modelos orientados a la simulación de sistemas en medicina y biología, debido a sus notables ventajas en el manejo de sistemas multidominio y multiescala presentes en estas aplicaciones.

Los gráficos de unión son una metodología gráfica de representación de sistemas dinámicos desde los cuales es posible obtener ecuaciones de estado que se resuelven para las variables de estado involucradas, con la finalidad de describir el comportamiento de un sistema a través del tiempo. Son comparables con otras técnicas gráficas como los diagramas de bloques o los diagramas de flujo, ampliamente utilizados en la representación de sistemas dinámicos, cuya principal característica es la manipulación de señales. En contraste, los gráficos de unión se basan en flujos de energía a través de sus vértices. Este rasgo los hace adecuados en el modelado de sistemas dinámicos que requieren una consideración rigurosa de las leyes de conservación, además permiten expresar de manera más expedita, la coexistencia e interacción de entidades cuyo comportamiento se enmarca en diferentes dominios energéticos (mecánicos, eléctricos, térmicos, hidráulicos, químicos, etc.), debido al uso del concepto universal de energía.⁷

Gracias a estos atributos, se ha visto cómo los gráficos de unión han incursionado de manera exitosa en diversas disciplinas. Por ejemplo, en Ingeniería Mecatrónica se ha realizado una gran producción investigativa, especialmente en el campo del control, cuya teoría ha podido ser adaptada a las características de los gráficos de unión. En el caso de la Ingeniería Mecánica se han llegado a encontrar aplicaciones en áreas como: dinámica,⁶ ingeniería de procesos y manufactura,⁸ mecánica de fluidos,⁹ transferencia de calor,⁶ entre otras. En menor medida, pero de igual importancia, ha sido la incursión de la metodología en otras especialidades como la Ingeniería Química,¹⁰ donde se ha logrado modelar reacciones químicas así como procesos en plantas químicas. Inclusive en disciplinas no ingenieriles ha habido casos de aplicación, por ejemplo, el comportamiento de sistemas económicos en el tiempo, como bien lo muestra John W. Brewer.¹¹

En relación con lo anterior, se hace evidente que debido a las grandes ventajas en el manejo de sistemas multidominio y multiescala, los gráficos de unión se vislumbran como una forma muy conveniente de plantear modelos de sistemas biológicos. Así pues, es posible, a partir de la aplicación de leyes fundamentales y de la adecuada aplicación de suposiciones, obtener un modelo con la suficiente complejidad para realizar un estudio detallado del funcionamiento de un sistema fisiológico que involucre el acoplamiento de elementos de diferentes dominios. Ahora, además de la comprensión de la fisiología de los sistemas, los gráficos de unión también son útiles para el diseño de implantes y la planeación de intervenciones quirúrgicas, como se puede ver en la sección de Aplicaciones de este trabajo.

 

FORMULACIÓN EN GRÁFICOS DE UNIÓN

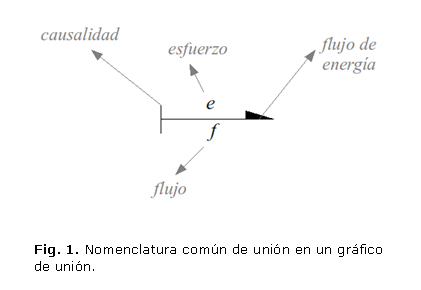
Los gráficos de unión (bond graphs) fueron creados por el Profesor Harry Paynter en 1959 y la metodología fue presentada por él mismo en 1962.¹² Estos son grafos dirigidos cuyos vértices son llamados "puertos" (ports) los cuales representan subsistemas, componentes o elementos básicos de un sistema. Las aristas del grafo (fig.1) se conocen como "uniones" (bonds) y representan el intercambio de energía entre los puertos a través de variables conjugadas de potencia, denominadas genéricamente esfuerzo e y flujo f (effort & flow), cuyo producto, en cualquier dominio energético representa potencia, por ejemplo: fuerza y velocidad, en un sistema mecánico de traslación, voltaje y corriente en el dominio eléctrico, y otras combinaciones que se muestran en la tabla 1. Adicionalmente, se definen las variables energéticas,⁷ designadas como momento y desplazamiento generalizados, que son respectivamente las integrales temporales del esfuerzo y el flujo. Estas se listan en la parte derecha de la mencionada tabla.

 

 

Elementos

Uniones

Las uniones o bonds son los elementos a través de los cuales fluye la energía de un puerto a otro. Cada unión tiene asociadas las variables conjugadas esfuerzo y flujo. Ahora, con el fin de establecer una dirección de referencia de flujo de energía, las uniones son medias flechas que apuntan en la dirección positiva del producto. Adicionalmente, una línea perpendicular a la unión es usada para representar la dirección del esfuerzo, de manera que hacia el lado opuesto al que esta puesta la línea, irá el flujo. Esta asignación de direcciones conocida como causalidad, requiere tener en cuenta el proceso que se lleva a cabo en cada puerto, por lo que en libros especializados,^6,13 se indica el procedimiento sistemático de asignación de causalidad en un gráfico de unión, en el que se hayan completado tanto las conexiones entre puertos como la asignación de direcciones de flujos de energía.

Puertos

Existen diferentes tipos de puertos dependiendo del manejo que se haga en ellos de la energía y de las variables energéticas (disipación, almacenamiento, transformación, etc.). Específicamente puede darse una clasificación:

Almacenamiento tipo I: También llamados, elementos inductivos o inerciales, son aquellos en los que la energía se almacena debido a la integración (acumulación) del esfuerzo e, resultando en la variable de estado p (momentum generalizado). Una masa con velocidad, un inductor eléctrico son ejemplos de la interpretación física de este tipo de puertos.

Almacenamiento tipo C: Este tipo de puertos representa la integración del flujo f con el fin de acumular la variable estado q (desplazamiento generalizado), por ejemplo, los resortes almacenan energía gracias a la elongación o compresión de este, un capacitor lo hace debido a una diferencia de voltaje, un tanque por diferencia de alturas, etc.

Elementos resistivos: Representados como R, son aquellos puertos donde la energía se disipa, ya sea por efectos de fricción en el caso mecánico, o por resistencia al flujo de corriente o fluido en los sistemas eléctricos e hidráulicos respectivamente.

Fuentes y sumideros: Son elementos que entregan o extraen energía del sistema, ya sea en forma de esfuerzo (Se) o de flujo (Sf). Mediante ellos se modelan las condiciones de frontera de los modelos, pues se consideran entidades externas al sistema.

Juntas

Las juntas son elementos de distribución instantánea de energía en los que no se realiza ninguna transformación, almacenamiento o disipación de esta.

Juntas 0: Es un multipuerto (puerto con varias uniones asociadas) en el que todos los esfuerzos de entrada y salida son iguales, mientras que la suma de los flujos debe ser igual a cero. Este elemento es análogo a un nodo en una red eléctrica, en el que se cumple la ley de corrientes de Kirchhoff.

Juntas 1: Es la contraparte de la junta 0 pues en este la constante es el flujo y la suma de esfuerzos es cero, equivalente a una malla eléctrica regida por la ley de voltajes de Kirchhoff.

Transformación reversible de energía¹³

Otros dos tipos de puertos conservativos son aquellos en los que el valor de potencia es igual en la entrada y en la salida.

Transformadores (TF): Implican la amplificación o reducción de cada una de las variables conjugadas de potencia, ya sea en uno o más dominios energéticos. La ecuación constitutiva de los transformadores relaciona el esfuerzo de entrada con el de salida mediante un módulo de transformación, mientras que los flujos se relacionan mediante su inversa. Algunos dispositivos que se modelan mediante este puerto incluyen reductores de velocidad, sistemas biela manivela, transformadores eléctricos, cilindros hidráulicos o neumáticos, etc.

Gyrators (GY): En este caso se relaciona el esfuerzo de entrada con el flujo de salida y el esfuerzo de salida con el flujo de salida mediante el mismo módulo, por lo cual esta abstracción se usa, generalmente, para describir procesos de transducción (transformación de una forma de energía en otra), como los que ocurren en motores eléctricos, bombas centrífugas, altavoces, etc.⁷

Modelado mediante gráficos de unión

Para alguien muy familiarizado con los gráficos de unión, estos pueden ser una abstracción directa del sistema físico estudiado, sin embargo, una representación gráfica más explícita e intuitiva puede ser necesaria con el fin de que los puertos y flujos de energía entre los componentes o subsistemas sean más evidentes (tabla 2). Algunas de estas representaciones incluyen redes de circuitos eléctricos, hidráulicos o neumáticos, diagramas de cuerpo libre, diagramas de bloques, diagramas de flujo, etc.

Karnopp y otros⁶ describen detalladamente, algoritmos de derivación de gráficos de unión para sistemas mecánicos (traslacionales y rotacionales), eléctricos, hidráulicos y térmicos, mientras que Borutzky,⁷ resume estos procedimientos para sistemas mecánicos y para otros sistemas (eléctricos, hidráulicos y térmicos), debido a que, para los primeros la variable de referencia es el flujo (velocidad) y para el resto es el esfuerzo (voltaje, presión, temperatura). A continuación se mencionan los pasos más generales:

· Identificar velocidades (esfuerzos para sistemas no mecánicos) y asignarles una junta 1 (0).

· Identificar elementos R, C e I y conectarlos a las respectivas juntas.

· Asignar flujos de energía de referencia, asumiendo todos los elementos de almacenamiento descargados, es decir, estos flujos se dirigen desde las fuentes hacia los elementos R, I, C y los sumideros de energía.

· Eliminar nodos de referencia.

· Simplificar el gráfico.

· Asignar causalidad.

El último paso es muy importante, ya que la asignación correcta de la causalidad repercute en el modelo matemático final, donde lo deseable es que todos los puertos se encuentren en causalidad integral.⁶ De otra manera se deben reconsiderar las suposiciones hechas a partir del modelo físico, hasta que el gráfico sea adecuado para continuar con la deducción de la representación de estado del sistema.

Finalmente, la obtención de una simulación a partir de la representación de estado se basa en la solución de las ecuaciones de estado que se obtengan del modelo gráfico. Existen métodos de obtención mediante algoritmos adecuados para ser programados en un ordenador,^6,7 de tales ecuaciones que suelen expresarse como sistemas de ecuaciones diferenciales ordinarias de primer orden, cuyas variables son las variables de estado que, en el caso de los gráficos de unión, suelen ser las variables energéticas (desplazamiento y momentum, generalizados). En este sentido se considera el siguiente procedimiento general:

· Escribir ecuaciones constitutivas para las fuentes independientes, es decir, aquellas que solo dependen del tiempo.

· Ahora se obtienen las relaciones para las fuentes controladas, las cuales dependen de la señal moduladora de entrada.

· Expresar las variables de salida de los elementos R en términos de las fuentes y los elementos de almacenaje de energía mediante propagación hacia atrás.

· Finalmente, se obtienen las relaciones entre las derivadas de las salidas de los puertos de almacenaje (C e I) como función de las salidas de fuentes, elementos resistivos y de otros elementos de almacenamiento.

Así, al solucionar estos sistemas de ecuaciones, analítica o numéricamente, se obtiene el comportamiento en el tiempo de cada una de las variables de estado involucradas en el modelo, las cuales, a su vez expresan el comportamiento transitorio del sistema físico con unas condiciones iniciales dadas y con condiciones de frontera propiamente impuestas.

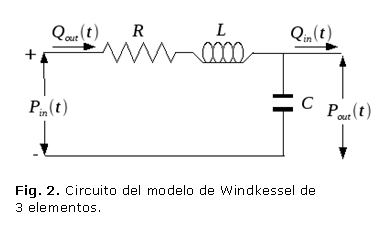
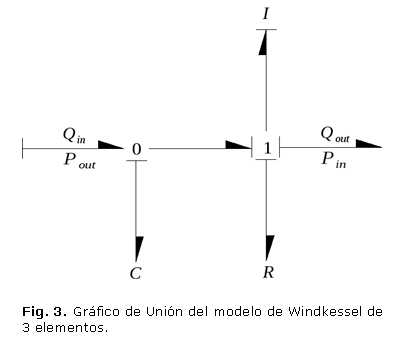
Para ilustrar mejor la manera en que lo anterior puede ser aplicado a un sistema real, se muestra la deducción del modelo sencillo de una parte del sistema cardiovascular humano. Un modelo sencillo de la red arterial (modelo de Windkessel (figura 2), propuesto por Shuzhen y otros,¹⁴ que tiene en cuenta la resistencia al flujo en las arteriolas y capilares, y la distensibilidad de las arterias mayores, se puede representar por el circuito de la figura 3.

 

 

 

El elemento R representa la nombrada resistencia, la capacitancia C, la distensibilidad y L es la inercia del fluido. En el circuito se puede observar que los elementos R, L están en serie, por lo que los dos se conectan a una junta 1, la cual conecta el sistema con una de las condiciones de frontera, además estos tres están en paralelo con la capacitancia de manera que la junta 1 se conecta a una junta 0 que interactúa con la otra frontera del sistema.

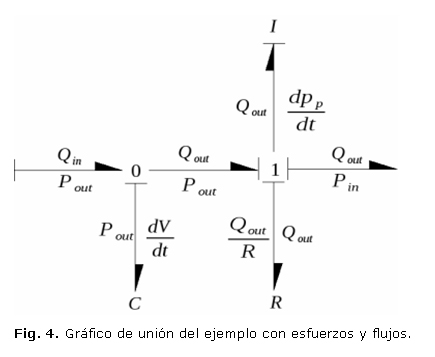
Ahora, mediante las ecuaciones constitutivas de los puertos 0 y 1, se pueden obtener los esfuerzos y flujos de cada unión como se muestra en la figura 4. De manera que al usar la convención de escoger las variables de estado como las variables de los elementos que almacenan energía que se encuentran en causalidad integral, se llega a que la primera variable es el volumen (integral del caudal) y la segunda es el momentum de presión (integral de la presión).

 

De nuevo, valiéndose de las ecuaciones constitutivas de las juntas se llega a:

 

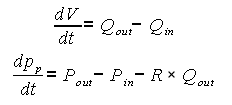
Ahora, es necesario que el sistema esté solamente en términos de las variables de estado, por lo que se usan las relaciones para puertos C e I de la tabla 2.

 

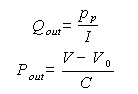
Donde V₀ es el volumen que puede contener el segmento sin que haya elongación o contracción de sus paredes. Entonces la representación de estado del modelo de Windkessel de tres elementos es:

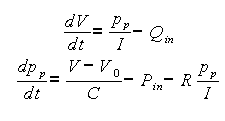
El ensamble de varios modelos de estos permite construir un modelo completo del sistema cardiovascular, en el cual cada modelo de Windkessel puede representar un vaso sanguíneo o una sección entera de vasos (brazo, pierna, cabeza, pulmones, etc.).

Gráficos de unión en un ordenador

Como consecuencia de la complejidad de un sistema dinámico real, un gráfico de unión puede ser tan intrincado como lo considere necesario el modelador, sin embargo, la deducción de la representación de estado a partir de un gráfico extenso, será una tarea engorrosa usando lápiz y papel, sin mencionar la labor necesaria para su solución. Por lo que, gracias a las herramientas computacionales omnipresentes actualmente, lo más natural es recurrir a un ordenador para lograr estos cometidos.

En atención a lo anterior existen diversos lenguajes de programación especialmente creados para el modelado y simulación de sistemas físicos, los cuales soportan el estándar creado en 1967: CSSL (Continuous System Simulation Languages). Entre estos, los más sobresalientes están: ACSL (Advance Continuous System Simulation Language), SIDOPS (Structered Interdisciplinary Description of Physical Systems) y Modelica, los cuales son descritos por Borutzky.⁷ Igualmente existen aplicaciones que soportan la simulación de modelos de sistemas dinámicos representados mediante redes de circuitos, diagramas de flujo, diagramas de bloques y gráficos de unión. Entre estos se encuentra el reconocido 20-SIM, el cual admite la introducción de los diferentes modelos gráficos mencionados.

Ahora bien, los programas y lenguajes mencionados y sus similares están enfocados hacia el modelado en aplicaciones en Ingeniería Mecatrónica, como el control de sistemas en los que intervienen componentes mecánicos, eléctricos, neumáticos e hidráulicos. Aplicaciones que en su gran mayoría están dirigidas a la automatización industrial de procesos, por lo que, en general, los análisis térmicos, químicos, de fluidos compresibles no newtonianos y de parámetros distribuidos no tienen relevancia, sin mencionar que el estudio de sistemas dinámicos de este tipo necesita una estructura computacional más robusta, debido a la complejidad de las relaciones matemáticas que describen los fenómenos físicos en estos dominios energéticos. Así, el modelado de sistemas dinámicos relevantes en biología y medicina (los cuales requieren de uno o más de los análisis mencionados, para lograr modelos sofisticados), usando las herramientas computacionales nombradas estaría supeditado a suposiciones que simplifiquen el modelo de manera que se adecue a las características del software. Adicionalmente, la discrepancia entre la terminología, nomenclatura y unidades usadas en sistemas mecatrónicos frente a las correspondientes en medicina y biología, es notable, lo cual puede generar problemas a los modeladores que no se encuentren familiarizados con el modelado del primer tipo de sistemas. Bajo ese razonamiento el camino a seguir en el desarrollo de modelos computacionales en medicina y biología usando gráficos de unión, es la creación de la herramienta computacional adecuada para tales fines.

Un programa destinado al modelado y simulación de sistemas biológicos mediante gráficos de unión debe poseer una generalidad adecuada en cuanto a la estructura de los gráficos y la versatilidad en la definición de las ecuaciones constitutivas de los puertos, las condiciones iniciales y las condiciones de frontera especificas de cada dominio energético.

En primera instancia se deben poseer bibliotecas de clases que permitan la definición de sistemas, subsistemas, puertos, uniones, bloques, etc. Como cualquier definición de clases, las usadas acá deben poseer métodos, propiedades, jerarquía (subclases), herencia. Igualmente, deben ser programadas diferentes subrutinas y funciones, las cuales realizaran diferentes acciones genéricas. A estas subrutinas se les puede llamar bien sea con objetos, matrices o escalares como entrada y del mismo modo sus salidas pueden ser de cualquiera de estos tipos.

La base del análisis del gráfico de unión se hace partiendo desde un archivo que contiene información acerca de este: subsistemas, puertos, conexiones, parámetros, condiciones iniciales, etc. Este archivo podrá ser generado por alguna aplicación gráfica, que a partir de un esquema dado por el usuario, genere información legible para el programa principal, las subrutinas y las funciones. Con respecto al formato de dicho archivo, Borutzky¹⁵ ya ha propuesto BGML, el cual está basado en el lenguaje XML y que puede contener la información mencionada anteriormente y algunos campos adicionales.

En ese orden de ideas, la primera subrutina (clasif): lee, clasifica y enumera los diferentes elementos del gráfico desde el archivo, empezando por los subsistemas en los que eventualmente se encuentre dividido el gráfico, después se deben identificar los elementos con base en el dominio energético al que pertenezcan, luego vienen las condiciones de frontera (modeladas como fuentes o sumideros) y finalmente a los elementos básicos (fuentes y sumideros externos, Capacitancias, Disipadores, Inertancias, Transformadores, Gyrators, juntas y uniones) se les debe asignar nomenclatura.

Entonces, relaciones constitutivas de los puertos se obtienen al llamar a la subrutina (constieq) que, mediante la clasificación de los puertos y el conocimiento de sus características y parámetros (linealidad, funciones de dependencia del tiempo y las variables energéticas, valores de constantes, etc.) aporta una o varias ecuaciones a la lista de ellas, que describe el sistema. Los parámetros y características se obtienen directamente del archivo de entrada.

Esta lista sirve de entrada a una subrutina (org) o programa de interoperatividad que haga la manipulación algebraica de las ecuaciones del modelo matemático obtenido, con el fin de llegar a un sistema de ecuaciones organizado para su posterior solución numérica, ya sea con otra subrutina (solve) que devuelve los valores de las variables de estado o con un programa externo que realice esta acción.

Entonces, una estructura aproximada de la rutina principal se verá como:

Principal (GU) /* Función principal cuya entrada es el Gráfico de unión (GU)*/

{

clasif /* Subrutina que enumera y clasifica cada elemento del GU */

Para el /* Para cada elemento del GU */

{

clase el(i) /* Definir cada elemento como objeto de la clase*/

Asign props /* Se asignan los parámetros y características para cada elemento como propiedades del objeto correspondiente*/

}

Para p /* Para cada puerto */

{

list(i) = constieq(i) /* Llamar subrutina de obtención de ecuaciones */

}

sist=org(list) /* Organizar ecuaciones */

solve(sist) /* Resolver sistema de ecuaciones */

}

 

GRÁFICOS DE UNIÓN EN BIOMÉDICA

Los campos de la biomédica que han visto la incursión de los gráficos de unión como herramienta de modelado incluyen los que se muestran en la tabla 3, donde se nombran algunos ejemplos de aplicación que se detallan más adelante.

Sistema cardiovascular

El sistema cardiovascular humano es un sistema cerrado, que tiene como función conducir la sangre a través de los pulmones y del sistema digestivo donde recibe oxígeno y nutrientes respectivamente. Entonces, esta es distribuida al resto del cuerpo para oxigenar y entregar los nutrientes a las células. Está compuesto por los vasos sanguíneos y el corazón. En su funcionamiento influyen factores de distintas índoles, que pueden ser encasillados, en uno o más dominios energéticos. Así pues, el sistema cardiovascular presenta interacciones químicas, transporte de fluidos, acción mecánica, transmisión de señales eléctricas y efectos térmicos.

En general los modelos de representación del sistema cardiovascular solo toman en cuenta las condiciones hidráulicas (presión y velocidad), sin incluir el efecto de los demás efectos físicos y químicos involucrados. Respondiendo a este vacío, Díaz-Zuccarini y otros,¹⁶ plantean un modelo de condiciones de frontera para el modelo de funcionamiento del ventrículo izquierdo del corazón. El artículo presenta una definición alternativa de tales condiciones utilizando gráficos de unión. De esta manera, emplea este planteamiento en la simulación de la apertura y cierre de la válvula mitral. Y gracias a la flexibilidad del software ANSYS/CFX, en cuanto a la definición de las condiciones de frontera, éste se utilizo para realizar la simulación del problema con las condiciones obtenidas a partir del método propuesto.

El artículo divide en tres partes la secuencia de asignación de condiciones de frontera: química, mecánica e hidráulica. Para las dos primeras se tiene en cuenta la transducción químico-mecánica que ocurre en las células cardiacas mediante un campo multipuerto C, para representar el almacenaje de energía en dos dominios diferentes, por un lado la energía química y por el otro la energía mecánica, que en concordancia con la definición de un puerto C mecánico, se refiere a un almacenaje de energía por desplazamiento. Es decir, se consideran las paredes del ventrículo compuestas por resortes que almacenan y dan energía dependiendo de la contracción de la cámara. En cuanto a las condiciones hidráulicas, se usa el modelo de gráficos de unión para calcular la presión impuesta por el ventrículo, la cual se calcula en cada iteración para ser usada como entrada en el modelo de elementos finitos. Finalmente, se impone una presión constante de 15 mmHg a la salida de la válvula.

Obtenida la representación con gráficos de unión, los autores deducen las ecuaciones de estado del sistema y proceden a acoplar este modelo con la simulación en elementos finitos del flujo de sangre a través de la válvula mitral. Entonces, los resultados de la simulación son presentados en gráficas contra el tiempo (posición angular del oclusor, presión en el ventrículo y velocidad angular del oclusor) las cuales confirman resultados experimentales.

Dependiendo del caso de estudio, muchas veces es deseable utilizar un modelo complejo para un sistema muy especifico, donde sean necesarios datos muy precisos, que necesiten ser usados en una investigación muy rigurosa, como la de Díaz-Zuccarini y otros.¹⁶ Pero en otras ocasiones, también es deseable tener una visión amplia del comportamiento de un sistema, es decir, tratar de abarcarlo de la manera más general posible. Pero un análisis extendido de un sistema complejo, requiere de un gran esfuerzo para lograr simulaciones medianamente aproximadas a la realidad, por lo que, algunas suposiciones deben ser hechas, dependiendo del nivel de detalle que se requiera de la simulación. En consecuencia, en un modelo del sistema cardiovascular estos aspectos deben ser tenidos en cuenta con el fin de garantizar un balance, entre el esfuerzo realizado para formular el modelo y la calidad de los resultados obtenidos de una simulación. Así, Zadpoor y otros,¹⁷ sugieren un modelo del sistema cardiovascular completo a través de gráficos de unión, usando un enfoque de parámetros concentrados o lumped parameters. En cuanto a las suposiciones hechas por los autores estas son: sangre como fluido newtoniano incompresible, venas y arterias como tubos cilíndricos de espesor y modulo de elasticidad constante. Además se hacen dos aproximaciones: primero, usar dos corazones, uno izquierdo y otro derecho y, segundo, tomar cada corazón como una fuente de esfuerzo modulado, que tenga en cuenta el efecto del flujo pulsativo de sangre producido por el órgano real. Finalmente, las válvulas cardiacas fueron modeladas como resistencias moduladas.

Del modelo gráfico los autores obtuvieron 20 ecuaciones diferenciales ordinarias de primer orden, que fueron resueltas en MATLAB, para un tiempo total de 4 segundos con un ciclo diástole-sístole de 0,8 s de duración. En cuanto al tiempo de integración, usaron 0,001 s. Los resultados obtenidos se presentan en gráficas de presión vs. volumen del corazón izquierdo, presión vs. tiempo del ventrículo izquierdo y caudal vs. tiempo en la aorta. Estos resultados fueron cotejados con datos obtenidos en otras simulaciones y así, los autores concluyen que el modelo es satisfactorio, lo que lleva a proponer que este sea acoplado con el que obtiene para el corazón Tabatabai en sus tesis de doctorado.¹⁸

Investigaciones similares del sistema cardiovascular usando gráficos de unión han sido realizadas por Le Rolle y otros^19,20 y por Dai y otros.¹⁴ De este último parte el estudio de la hipertensión que es llevado a cabo por Chen y otros²¹ usando el mismo modelo al cual se le añaden el cálculo del consumo de oxígeno en cada latido del corazón y el espesor de pared del ventrículo izquierdo.

Sistema musculoesquelético

La percepción general es que el sistema musculoesquelético es responsable del movimiento o locomoción del cuerpo, por lo cual, su estudio muchas veces se limita a la dinámica de sus componentes, huesos y músculos, al considerar los primeros como eslabones rígidos de un mecanismo, que se conectan mediante juntas que permiten rotación relativa, mientras que a los segundos en general se les modela como un resorte y un amortiguador en paralelo. Además, se suele ignorar la presencia de ligamentos y tendones, debido a que se suponen ideales, las uniones entre los huesos (articulaciones) y también las conexiones entre los músculos y los huesos. Pero, a pesar de que la cinemática y la cinética son el objetivo principal del estudio de este sistema, hay que tener en cuenta que en su comportamiento, se ven involucrados también fenómenos químicos, como el mecanismo de transformación de energía química en energía mecánica de se da en los músculos, y fenómenos eléctricos como la transmisión de señales a través del sistema nervioso central, por medio de potenciales de acción, hasta las motoneuronas que a su vez envían potenciales de acción a través de las uniones neuromusculares a las fibras musculares. Asimismo, dentro de las fibras musculares ocurren complejos procesos eléctricos que dan como resultado la contracción del músculo.

De esta manera, se han propuesto diversos modelos de funcionamiento de la contracción muscular, en los que se han tratado de incluir algunos de los fenómenos mencionados. Uno de estos modelos es presentado por Laura Wojcik,²² en el cual el miembro inferior de una persona que trata de mantener el equilibrio es el objeto de estudio, dicho modelo está compuesto por dos secciones (two-lump): muslo y pierna, para los cuales se tienen en cuenta los efectos de rotación, representados mediante transformadores modulados (que describen cambios de sistema coordenadas). Adicionalmente, el comportamiento de los músculos se describe mediante el modelo de Hill, que es un enfoque en el que se tiene en cuenta la longitud instantánea del músculo, su velocidad de acortamiento y activación, siendo esta última, la que describe el lapso entre la excitación neural y la contracción de este. Dicho modelo, en el gráfico de unión se implementa mediante fuentes moduladas por los puertos que representan los centros de gravedad de muslo y pierna.

Ahora, como se mencionó al inicio de esta sección, el estudio de la dinámica y de resistencia de materiales del sistema músculo esquelético es el objeto de muchas investigaciones, bajo diferentes metodologías de modelado, sin ser los gráficos de unión la excepción. Sendos artículos se han escrito sobre ello, uno por Vaz y compañía²³ sobre el mecanismo de extensión de un dedo de la mano humana y otro por Contreras y Roa²⁴ quienes proponen un modelo en gráficos de unión de la marcha humana.

En cuanto al primero, una primera aproximación a través de objetos de gráfico de unión en palabras (WBGO) se plantea con el fin de hacer un primer acercamiento, de manera más intuitiva al proceso realizado para la obtención del gráfico de unión verdadero, no sin antes, dar una pequeña descripción del funcionamiento del mecanismo y explicar las suposiciones e innovaciones de este modelo. En seguida se presentan los principales aspectos de deducción de las ecuaciones constitutivas para los puertos que se usan. El enfoque utilizado para la representación en gráficos de unión, es una formulación de dinámica de cuerpos rígidos introducida por Karnopp⁶, donde las falanges son consideradas como eslabones, y las articulaciones como uniones con comportamiento visco elástico debido al efecto del cartílago suave; En el gráfico de unión verdadero, este aspecto se representa mediante puertos C y R. La actividad muscular es considerada como la acción de una configuración de resortes-tubo. Y la forma como la red de tendones actúa sobre las falanges se aproxima mediante el modelo topológico de los rombos de Winslow (Winslow's Rhombus).

El segundo artículo, publicado por Contreras y Roa en el 2005,²⁴ corresponde a la tesis de maestría del primero. En él se presenta un modelo en gráficos de unión de la caminata humana. El objetivo es el modelado y simulación de una representación en siete eslabones (cadera, muslos, piernas y pies) con 20 grados de libertad en el que adicionalmente se consideran los extremos distal y proximal de muslo, pierna y pie; es decir, a diferencia de otros modelos, en este se tiene en cuenta que el centro de masa de cada eslabón no está en su centro geométrico. De la simulación de este modelo se obtienen: torques, fuerzas intersegmentales y potencia en articulaciones. Esta información posteriormente es comparada con datos experimentales, obtenidos de una prueba en un laboratorio de marcha, los cuales se procesan con un software especializado que proporciona gráficas de variables cinemáticas y cinéticas con respecto al tiempo.

Los gráficos de unión se obtuvieron por dos técnicas: modelos multipuertos de Karnopp y análisis cinético (propuesto por los autores). Estos se simularon en el programa 20-SIM para las entradas correspondientes al modelo inverso de aproximación dinámica (expresa fuerzas y pares en función de la evolución de las coordenadas articulares y sus derivadas), o sea: datos antropométricos, posición inicial y velocidad angular y datos de fuerza de reacción del piso. Así pues, la información obtenida de la simulación es representada en gráficas de momentos y potencias de las articulaciones contra el tiempo; y la gráfica de momento en la cadera es comparada con los datos experimentales obtenidos de la prueba de marcha.

En cuanto a las conclusiones y el trabajo futuro, los autores sugieren la utilización de los gráficos de unión para la realización de modelos tridimensionales de la marcha humana y en los que además se tengan en cuenta eslabones adicionales (miembros superiores).

Un trabajo adicional de Vaz y otros²⁵ trata sobre el diseño y simulación de una prótesis para una mano en la que haya ausencia de uno o más dedos.

Aplicaciones

A través de este documento se han estado explorando modelos relacionados con el funcionamiento de un sistema fisiológico bajo condiciones normales, y con fines de validación de los modelos. Pero los modelos de sistemas pueden ser usados, además, como herramienta de diseño de dispositivos y planeación de procedimientos. En el caso particular del campo de la biomédica, se trata del diseño de implantes y aparatos de asistencia en una cirugía. Adicionalmente, de los datos obtenidos de una simulación puede hacerse una planificación más precisa de una intervención quirúrgica que requiera una ejecución bajo condiciones muy especiales.

Los aspectos mencionados arriba son abordados en dos trabajos, uno por Romero y otros²⁶, y otro por Bwunghoon Bae y otros.²⁷ En el primero se expone el análisis de viabilidad de un dispositivo para el tratamiento del glaucoma. Este consiste de un implante que regula la presión intraocular (IOP), considerada un factor de riesgo cuando se encuentra por encima de valores estándar. El artículo comienza analizando dos de los implantes convencionales más utilizados, la válvula Ahmed y la válvula Molteno, dispositivos que reducen la IOP drenando el humor acuoso de la cavidad ocular. La regulación se hace mediante tubos de silicona y membranas que actúan como resistencias al paso del fluido. La principal desventaja de estos dispositivos es que no pueden realizar una regulación dinámica que permita restablecer la presión normal ante fluctuaciones de la IOP dentro del globo ocular; Tales variaciones son dependientes del paciente tratado. Para mitigar este problema, los autores proponen el diseño de un nuevo implante activo, que permita la regulación deseada a través de un sistema de control capaz de detectar los cambios de la IOP y modificar el flujo de liquido a través de la válvula.

Específicamente, los gráficos de unión obtenidos en el artículo corresponden solo a la parte concerniente a la válvula de los dispositivos analizados (los clásicos y el propuesto). En el caso de los dispositivos convencionales, el gráfico de unión es, como se esperaba, sencillo debido a que el modelo es simplemente un conducto con una membrana que actúa como válvula, restringiendo el paso de fluido. El flujo proveniente de la cavidad ocular se toma como una fuente de flujo y la flexibilidad de la membrana se modela como un resorte que actúa sobre la masa de la misma. En el caso del dispositivo propuesto, este se vale del mismo principio de la membrana como válvula, solo que esta vez la membrana es ajustada mediante un actuador electromagnético, con el fin de modificar el flujo a través del tubo de silicona. Entonces, el gráfico de unión obtenido incluye la representación del dispositivo adicional, donde ahora se tienen en cuenta, la masa del magneto permanente, la interacción de este con la membrana (que se modela con una capacitancia y una resistencia), y el modelo del sistema de fuerza magnetomotriz que genera el movimiento del magneto a partir del voltaje y corriente de entrada.

Entonces, para corroborar los resultados obtenidos, los autores realizaron un experimento in vitro del dispositivo y se concluye que el modelo teórico se aproxima razonablemente a los resultados obtenidos experimentalmente.

Ahora, modelos del sistema cardiovascular fueron tratados en la sección dedicada a éste, pero como se vio, estos están enfocados hacia la comprensión del funcionamiento total o parcial del sistema. Sin embargo, en esta sección se hace una breve reseña de un trabajo relacionado con el modelado y simulación de un tratamiento de emergencia experimental para intervenir a un paciente que haya tenido un accidente cerebro vascular o stroke, el cual es una de las mayores causas de muerte en el mundo. El 85 % de las veces, estos se producen por una obstrucción debida a coágulos de sangre que se forman en algún lugar del cuerpo y viajan a través del torrente sanguíneo hasta el cerebro. El tratamiento más común que se aplica a un paciente que sobrevive a este suceso, es la trombolisis,²⁶ que consiste en la disolución del coágulo que produce el bloqueo. Pero hay ocasiones en que este procedimiento no puede ser realizado. En estos casos se puede recurrir a la trombectomía, procedimiento quirúrgico consistente en la extracción del elemento obstructor del vaso sanguíneo. La forma de hacerlo es mediante un dispositivo experimental llamado `GP' Thrombus Aspiration Device (TAD) que, como su nombre lo indica, realiza la extracción del coágulo mediante la succión producida por una bomba de vacío que se conecta mediante un catéter al dispositivo `GP' que es el elemento final de succión que se introduce en el vaso sanguíneo.

Con respecto al funcionamiento de este dispositivo experimental, Romero y otros²⁶ presentan un modelo y simulación de las fuerzas de adhesión, entre el coágulo y la pared del vaso sanguíneo, que en este caso es una arteria cerebral. Esto con el objetivo de determinar la presión mínima de extracción, utilizando diferentes tamaños de coágulo y distintos valores de fuerza de adhesión, pues esta depende del tiempo de residencia del coágulo en la arteria (a mayor tiempo de estadía, mayor fuerza de adhesión). Se realiza un gráfico de unión en el que los autores incluyen dos elementos resistivos: la fuerza de fricción del coágulo con la pared de la arteria y la pérdida debida a la diferencia de diámetros entre el coágulo y el elemento de succión. También hay elementos tipo C (rigidez del coágulo y de la pared de la arteria) y tipo I (masa del coágulo).

Con el modelo anterior completo, se realizaron las simulaciones para las condiciones especificadas y se encontraron los valores mínimos de presión para la extracción de coágulos de diferentes diámetros con distintos tiempos de residencia (fuerzas de adhesión), junto con los tiempos de extracción para cada presión. Tiempos que según los autores están dentro de los límites clínicos, para que el procedimiento pueda ser aplicado en un paciente.

 

PERSPECTIVAS

La comprensión de los modelos fisiológicos y patológicos en un organismo, como se ha demostrado, no es de interés solo de biólogos y médicos. Matemáticos, físicos e ingenieros han colaborado en el aumento del conocimiento sobre los principios que rigen los procesos físicoquímicos involucrados en cualquier organismo biológico. Diversas metodologías han sido utilizadas a lo largo de los años como herramientas de modelado matemático de estos procesos, encontrando soporte en la computación para simulaciones y obtención de resultados útiles. Pero, como lo explican los autores citados en este documento, estos enfoques en general han carecido de precisión en los datos arrojados por el modelo cuando se comparan con resultados experimentales. O han sido complicados, tanto así, que el requerimiento computacional en las simulaciones ha sido tan alto que su fiabilidad en los resultados no justifica su aplicación. Adicional a lo último, cabe anotar que los modelos complicados no suelen ser fáciles de relacionar con los fenómenos observables, lo cual es útil para hacer manipulaciones y/o acciones de control, sin necesidad de replantear el modelo. Ahora bien, a lo largo de este artículo se ha estado mostrando la superioridad de los gráficos de unión en estos aspectos respecto a técnicas tradicionales, pero es evidente, que pese a haber transcurrido cincuenta años desde su invención el uso como herramienta de modelado ha sido escaso en la biomédica. Es una situación singular dado que, como demuestran los artículos analizados, la metodología es más que adecuada en el tratamiento de sistemas biológicos, gracias a sus bien conocidas ventajas en el manejo de sistemas multidominio, dentro de los cuales encajan los problemas biomédicos. Entonces, no es objeto de este artículo entrar a discutir las razones de esta tendencia, pero cabe anotar que J. LeFèvre y otros ya han hecho una breve reseña del tema.²⁸

Ciertamente, en varios campos de la biomédica, ha habido aplicaciones de los gráficos de unión, pero como se dijo arriba, se esperaría que en cada una de estos, la cantidad de investigaciones y de modelos fuese mayor. Ahora, gracias a la difusión que en estas últimas dos décadas, ha tenido la metodología en revistas científicas y libros, no solo en biomédica sino en muchos otros campos, la tendencia por parte de los investigadores será hacia, el estudio de la técnica, la comprensión de los trabajos existentes y finalmente, el desarrollo de modelos más completos en cada disciplina, y la expansión de la herramienta a otros campos de la biología y la medicina.

Por ejemplo, en el caso de los modelos del sistema cardiovascular, se realizarán análisis más complejos, con menos suposiciones, en los que se incluyan diversos efectos relacionados con el comportamiento de la sangre dentro de los vasos sanguíneos, condiciones geométricas del corazón, mejores aproximaciones a los procesos químicos involucrados en la transducción de las ordenes neurológicas a la contracción mecánica del órgano cardiaco. De manera que el análisis de enfermedades y tratamientos estará supeditado al refinamiento de estos modelos en el área de interés. Será entonces la oportunidad para que los bond graphers seleccionen el grado de complejidad que cada problema requiera, es decir, ¿Cuántos sistemas están involucrados en el fenómeno?, ¿Es necesaria la inclusión de procesos químicos? ¿Se pueden asumir las relaciones constitutivas de los puertos, lineales? o por el contrario, ¿Hay que valerse de ecuaciones más sofisticadas? ¿Puede la sangre, ser tratada como fluido newtoniano? Las respuestas a estas preguntas, podrán ser implementadas rápidamente en el diagrama general del modelo, debido a la ampliamente nombrada flexibilidad de los gráficos de unión en este aspecto.

Los procedimientos quirúrgicos serán optimizados utilizando procedimientos similares a los mostrados por Romero y otros,²⁶ incluyendo intervenciones de corazón, en las cuales, la correcta selección de los parámetros es vital. En este sentido los gráficos de unión tendrán un papel importante, pues, como se muestra en el artículo citado, con estos se tiene la capacidad de simular, tanto el comportamiento biológico del paciente, como el funcionamiento de los dispositivos que se usen en la operación.

En cuanto al sistema musculoesquelético, el rumbo a seguir es un poco más evidente gracias a lo demostrado por los autores citados. Evidente en cuanto a que lo más natural es construir gráficos de unión que acoplen el modelo refinado del comportamiento del músculo (modelo de Hill) planteado por Wojcik,²² con los modelos enfocados en la dinámica de Contreras y Roa²⁴ y con el de Anand Vaz,²³ dependiendo del caso de estudio. En otras palabras, el modelo de Hill para los músculos brindaría aún más fiabilidad a los datos cinemáticos y dinámicos que se puedan obtener con el modelo del mecanismo de extensión del dedo. De forma similar, se podría aplicar el gráfico de unión del modelo de Hill con el presentado por Contreras y Roa, de la marcha humana, al usar el primero como modelo de condiciones de frontera del segundo. Es decir, los datos de fuerza obtenidos del músculo serian entradas para el modelo de la marcha humana (que en este caso usaría el enfoque dinámico directo: evolución temporal de las coordenadas en función de fuerzas y pares), y los resultados devueltos por este ultimo realimentarían el modelo propuesto por Wojcik,²² pues como se dijo arriba, este modelo tiene en cuenta la longitud del musculo para determinar su fuerza efectiva.

Finalmente, con respecto al artículo que trata sobre el implante ocular para la regulación de la presión intraocular (IOP), hay que decir que es un muy buen complemento al trabajo realizado por Romero y otros,²⁶ en el sentido de que es la confirmación del potencial que tienen los gráficos de unión en el diseño y planeación de intervenciones quirúrgicas, en las que se requiera la utilización de dispositivos o aparatos que presentan interacción con órganos y tejidos del cuerpo. Como bien se describe en los artículos citados, para realizar cualquier procedimiento de esta clase, ya sea una acción correctiva mediante algún instrumento o mecanismo, o la inserción de algún implante, es necesario planificar de la manera más exhaustiva posible, y así evitar cualquier efecto perjudicial en el organismo, ya sea por errores en la realización del procedimiento o por problemas derivados de la incompatibilidad de los materiales usados en estos dispositivos. Así pues, el aporte de los gráficos de unión en esta etapa es crucial ya que, como se puede observar en los resultados obtenidos por los autores en sus respectivas investigaciones, la fiabilidad de las simulaciones con respecto a los experimentos es la adecuada, sin perder la simplicidad y sencillez en la representación de los fenómenos estudiados.

Como consecuencia de lo anterior, se puede comprender que trabajos futuros en el campo de los implantes oculares y en general, cualquier tipo de intervención quirúrgica que involucre dispositivos o aparatos de índole electromecánica, contarán con modelos y simulaciones fiables y precisas, gracias a las capacidades que tienen los gráficos de unión para lidiar con las dificultades que presenta la coexistencia de sistemas electromecánicos, construidos por el hombre con sistemas biológicos, que deben cooperar con el propósito de corregir falencias de estos últimos. Es así, como en trabajos futuros, intervenciones quirúrgicas relacionadas con la visión, como la cirugía láser, la cirugía de cataratas, la cirugía reflectiva, la cirugía de córnea, etc. serán analizadas, diseñadas y planeadas mediante el uso de modelos y simulaciones basados en gráficos de unión, en los que dependiendo del caso, los investigadores realizarán experimentos para encontrar valores de parámetros no determinables teóricamente y también para la validación de los modelos propuestos.

 

CONCLUSIONES

Mediante la información recopilada se pueden hacer algunas reflexiones sobre la situación actual y se aventuran algunas predicciones sobre el porvenir de los gráficos de unión como instrumento de la comprensión de los sistemas fisiológicos. Este conocimiento puede ser usado en el desarrollo de nuevas técnicas y estrategias de modelar enfermedades y problemas complejos relacionados con la ingeniería biomédica. A partir de la información aquí recopilada se puede concluir que este tipo de técnicas pueden ser utilizadas para abstraer fenómenos biomédicos que evolucionen en el tiempo y que sean modelados por ecuaciones diferenciales múltiples de primer y segundo orden. Un caso específico de estas ecuaciones son aquellas relacionadas con flujos de fluido (problemas sanguíneos) y eléctrico (nervioso). Esta técnica se puede combinar con otras para establecer mecanismos de predicción potentes en el estudio de patologías y fenómenos médicos.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Bergeron BP, Greenes RA. Modeling and Simulation in Medicine: The State of the Art. 1988. p. 282-6.

2. Crampin EJ, Halstead M, Hunter P, Nielsen P, Noble D, Smith N, et al. Computational physiology and the physiome project. Experimental Physiology. 2003;89(1):1-26.

3. Thomaseth K. Multidisciplinary modelling of biomedical systems. Computer Methods and Programs in Biomedicine. 2003;71(3):189-201.

4. Stiles JR, Ford WC, Pattillo JM, Deerinck TE, Ellisman MH, Bartol TM, et al. Spatially realistic computational physiology: past, present and future. Advances in Parallel Computing. 2004;12:685-94.

5. Diaz-Insua M, Delgado M. Modeling and Simulation of the Human Cardiovascular System with Bond Graph: a Basic Development. Computers in Cardiology. 1996;393-6.

6. Karnopp DC, Margolis DL, Rosemberg RC. System Dynamics Modelling and Simulation of Mechatronic Systems. New Jersey: John Wiley & Sons, Inc; 2006. Pp 1-250.

7. Borutzky W. Bond Graph Methodolgy, Development and Analysis of Multidisciplinary Dynamic System Models. London: Springer; 2010.Pp 1-657.

8. Applications of bond graphs to modelling industrial processes and manufacturing systems. Bond Graphs in Control, IEE Colloquium on. London. 1990. p. 4/1-4/8.

9. Baliño JL, Larreteguy AE, Gandolfo Raso EF. A general bond graph approach for computational fluid dynamics. Simulation Modelling Practice and Theory. 2006;14(7):884-908.

10. Couenne F, Jallut C, Maschke B, Tayakout M, Breedveld P. Bond graph for dynamic modelling in chemical engineering. Chemical Engineering and Processing: Process Intensification. 2008;47(11):1994-2003.

11. Brewer JW. Progress in the bond graph representations of economics and population dynamics. Journal of the Franklin Institute. 1991;328(5-6):675-96.

12. Paynter HM. Analysis and Design of Engineering Systems. Cambridge, Massachusetts, USA: MIT Press; 1961.

13. Borutzky W. Bond graph modelling and simulation of multidisciplinary systems An introduction. Simulation Modelling Practice and Theory. 2009;17(1):3-21.

14. Dai K, Ning G, Chen S, Du J, Zheng X. Simulating Cardiovascular Haemodynamics by Bond Graph Technique. IFMBE. 2007;14(1):151-4.

15. Borutzky W. BGML - a novel XML format for the exchange and the reuse of bond graph models of engineering systems. Simulation Modelling Practice and Theory. 2006;14:787-808.

16. Díaz-Zuccarini V, Rafirou D, LeFevre J, Hose DR, Lawford PV. Systemic modelling and computational physiology: The application of Bond Graph boundary conditions for 3D cardiovascular models. Simulation Modelling Practice and Theory. 2009;17(1):125-36.

17. Zadpoor AA, Arshi AR, Nikooyan AA. A Bond Graph Approach to the Modeling of Fluid-Solid Interaction in Cardiovascular System's Pulsatile Flow. Proceedings of the 2005 IEEE. Engineering in Medicine and Biology 27th Annual Conference. Shanghai, China; 2005. p. 2319-22.

18. Tabatabai F. Spatiotemporal wavefront propagation in 3D geometric excitable heart tissue. Irán: Amirkabir University of Thech; 2004.

19. Le Rolle V, Hernandez A, Richard PY, Buisson J, Carrault G. A model of the cardiovascular system using Bond Graphs. Acta Biotheor. 2005;54(4):295-312.

20. Le Rolle V, Hernandez A, Richard PY, Buisson J, Carrault G. A model of the cardiovascular system using Bond Graphs for the analysis of the autonomic nervoys system. ITBM-RBM. 2005;26:333-43.

21. Chen S, Zhang S, Gong Y, Dai K, Sui M, Yu Y, et al. The role of the autonomic nervous system in hypertension: a bond graph model study. Physiological Measurement. 2008;29(4):473-95.

22. Wojcik LA. Modeling of musculoskeletal structure and function using a modular bond graph approach. Journal of the Franklin Institute. 2003;340(1):63-76.

23. Vaz A, Singh K. A bond Graph Model for the Extensor Mechanism of Human Finger. Durgapur, India: 14th National Conference on Machines and Mechanisms. Diciembre de 2009. p. 139-45.

24. Contreras Bravo LE, Roa Garzón MA. Modelamiento de la marcha humana por medio de gráficos de unión. Tecnura. 2005;8(16):26-42.

25. Vaz A, Hirai S. Bond Graph Based Design of Prosthesis for Partially Impaired Hands [Internet]. [cited 2012 Sep 21]. Available from: http/:www.mint.se.ritsumei.ac.jp/project/COE/HUT-RITS-2004/Proc/Vaz.pdf

26. Romero G, Higuera I, Martinez ML, Pearce G, Perkinson ND. Analysis and simulation of the adhesion forces between clot and the artery wall for a novel thrombectomy device applied to the middle cerebral artery. Cambridge, UK: UKsim; 2010. p. 195-200.

27. Bae B, Kim N, Kee H, Kim S-H, Lee Y, Lee S, et al. Feasibility Test of an Electromagnetically Driven Valve Actuator for Glaucoma Treatment. Journal of Microelectromechanical Systems. 2002;11(4):344-54.

28. LeFèvre J, LeFèvre L, Couteiro B. A bond graph model of chemo-mechanical transduction in the mammalian left ventricle. Simulation Practice and Theory. 1999;7(5-6):531-52.

 

Recibido: 10 de septiembre de 2011.
Aprobado: 25 de septiembre de 2011.

 

 

Diego Edgardo Fuentes Herrera. Universidad Nacional de Colombia. Correo electrónico: [e-mail]