Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Investigaciones Biomédicas
versión On-line ISSN 1561-3011
Rev Cubana Invest Bioméd vol.33 no.3 Ciudad de la Habana jul.-set. 2014
ARTÍCULO ESPECIAL
Generación de imágenes tridimensionales: integración de tomografía computarizada y método de los elementos finitos
3D imaging: integration of computerized tomography and the finite element method
Ing. Yosbel Angel Cisneros Hidalgo,I Dr. C. Raide Alfonso González Carbonell,I Dr. Antonio Puente Alvarez,II Ing. Ernesto Camue Corona,I Ing. Yuri Oropesa Rodríguez I
I Facultad de Electromecánica, Universidad de Camagüey. Camagüey, Cuba.
II Hospital Provincial Clínico Quirúrgico Docente "Amalia Simoni". Camagüey, Cuba.
RESUMEN
Se trata la posibilidad de utilización de las nuevas tecnologías y en especial la Tomografía Axial Computarizada (CT) utilizando como herramienta modeladora el Método de los Elementos Finitos (MEF) para la generación de volúmenes 3D que puedan ser empleados en la obtención de modelos mecano-biológicos aplicables a afecciones ortopédicas.
Palabras clave: tomografía axial computarizada, ortopedia, método de los elementos finitos, modelos mecano-biológicos.
ABSTRACT
This work deals about the possibility of using new technologies and especially the Computed Tomography (CT) using shaper tool as the Finite Element Method (FEM) to generate 3D volumes that can be employed in obtaining it mechanical-biological models applicable to orthopedic conditions.
Keywords: computerized axial tomography, orthopedics, finite element method, mechanobiological models.
INTRODUCCIÓN
Con el rápido desarrollo de la tecnología de los medios computacionales, se ha implementado vertiginosamente el uso de imágenes médicas en el campo de la salud. Con dichas imágenes es posible observar diversas partes del cuerpo humano,1 como el estómago, la cabeza, la cara, la espalda, el pecho y otras, con el fin de ayudar a los médicos y especialistas a diagnosticar alguna afección del paciente (tumores, cáncer). Además, permiten cuantificar en uno u otro grado enfermedades específicas, como la osteoporosis, sin la necesidad de someter al paciente a métodos invasivos como la cirugía.2-4
Con la aplicación de los tomógrafos se obtiene un volumen de información bastante elevado. Sin embargo, el uso eficiente de estas grandes cantidades de datos de imágenes está limitado por el nivel actual de procesamiento de imágenes, la experiencia del doctor y por algunos factores subjetivos como el nivel de agotamiento físico del médico, y otros como el estado técnico del tomógrafo o las precauciones tomadas por el tecnólogo encargado de operar el equipo. Por tanto, es conveniente una adecuada formación de imágenes, segmentación, transferencia y clasificación por el software de ordenador.
Cómo procesar todos los datos de imagen disponibles y hacer, entonces, un diagnóstico asistido por ordenador (CAD) es una de las últimas investigaciones llevadas a cabo por ingenieros, médicos y personal de la salud. Recientemente, algunas investigaciones se centran en este campo específico.5 El-Bazl6 propuso un sistema CAD basado en la característica simétrica de pulmón y en el hecho de que los tumores parecen ser redondos. Estos métodos son eficaces para algunos pacientes específicos.
Sin embargo, cabe destacar que tales poderosas herramientas a veces no se pueden emplear debido a que el algoritmo utilizado para el procesado de las imágenes no puede brindar resultados óptimos, debido fundamentalmente a la heterogeneidad del cuerpo humano.7
En este artículo se presentan las posibilidades que brindan las imágenes médicas para la obtención de geometrías complejas del cuerpo humano útiles para el modelado de órganos, tejidos y huesos, empleando para su análisis computacional el método de elementos finitos. Así, el objetivo de este trabajo es describir el uso de la TAC integrada con el método de los elementos finitos (MEF) como herramienta modeladora para la generación de volúmenes tridimensionales que puedan ser empleados en la obtención de modelos mecanobiológicos aplicables a afecciones ortopédicas.
MÉTODOS
El método de elementos finitos (MEF) como herramienta constituye posiblemente el método más usado en el diseño de aeroplanos, máquinas y puentes.8 Recientemente, se ha incorporado en el modelado de funciones y partes del cuerpo humano a través de soluciones numéricas basadas en el cálculo de ecuaciones diferenciales parciales (EDP).9 Usando un software especial es posible modelar estructuras muy complejas gracias a la discretización de los elementos en pequeños diferenciales de área llamados elementos finitos, los cuales son fáciles de caracterizar y modelar matemáticamente.9
Para la obtención de la correcta geometría del tejido, hueso u órgano implicado en el análisis se hace necesaria la implementación de un sistema de imágenes que permita obtener de forma bastante exacta todos los contornos e irregularidades que pueda presentar el objeto observado.10 En la actualidad es común encontrar la integración del MEF con el diseño asistido por computadora (CAD) con el objetivo de integrar en una sola aplicación el diseño y el cálculo, posibilitando la disminución del tiempo de desarrollo y puesta a punto del producto.
Procedimiento genérico empleado por el MEF
La idea básica es muy simple: se asume que el problema físico puede ser resuelto mediante ecuaciones diferenciales parciales (EDP) las cuales son definidas en una geometría compleja,11 como por ejemplo, una tibia humana. Debido a esta compleja geometría, es necesario llevarla a formas más simples, momento donde entra en función el MEF, el cual convierte la compleja estructura en pequeñas formas espaciales (triangulares, tetraédricas, hexaédricas, etc.) y cada elemento es procesado de manera individual. Se pueden resumir en cuatro las operaciones llevadas a cabo por el MEF para el modelado de un ente geométrico:
- Generación de una representación genérica del objeto. La generación del mallado es una operación crucial para el resto del proceso e influye de forma decisiva en la exactitud del resultado final. A veces se hace necesario un refinamiento del mellado en zonas específicas para obtener mayor exactitud en la simulación.
- Definición del comportamiento físico. Para lograr obtener un modelo que se acerque lo más posible a la realidad. Para ello es necesario definir dos características fundamentales: el material y las condiciones de frontera.
- Configuración de la matriz de rigidez. Para cada diferencial de área o elemento finito es necesario conformar una matiz de rigidez, de lo cual el software se encarga automáticamente. Después de generadas las matrices individuales se obtiene una general llamada K, para todo el sistema.
- Solución numérica del problema.
ANÁLISIS DE LOS RESULTADOS Y DISCUSIÓN
Obtención de imágenes volumétricas. Modelos geométricos
El modelo geométrico es obtenido mediante la segmentación de las imágenes tomadas por el tomógrafo y posteriormente reconstruidas gracias a poderosos algoritmos matemáticos.1 Muchos factores pueden influir en la calidad de la segmentación, como por ejemplo la compleja estructura del organismo humano, posibles deformaciones degenerativas que pueda presentar el paciente, difícil acceso a la zona deseada debido a elementos perturbadores que rodean la frontera del objeto en cuestión o estructuras similares a la deseada que dificulten la selección adecuada.10
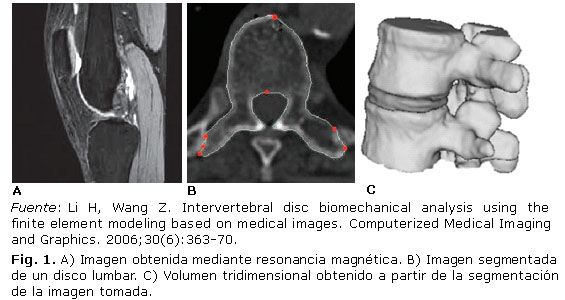
La aplicación de la tomografía computarizada (TC) posibilita a los doctores en medicina obtener mayor contraste en la obtención de las imágenes relacionadas con el tejido óseo comparadas con otros métodos de obtención de imágenes como la resonancia magnética nuclear (RMN), en la cual se obtienen contornos mucho más oscuros, pero a su vez permite obtener muestras de imágenes de ligamentos y músculos.7, 12 En la figura 1A se puede observar una imagen médica de la unión tibiofemoral tomada mediante RMN donde se observan los ligamentos y músculos. En la figura 1B se muestra el resultado de la segmentación de la imagen, y en la figura 1C, el volumen tridimensional reconstruido a partir de la segmentación anterior.
Características del proceso de segmentación de imágenes
La segmentación de las imágenes se hace para definir estructuras anatómicas dentro del volumen de imágenes obtenidas.14 Este procesamiento de imágenes es un paso importante en la obtención del volumen 3D y crucial para la calidad de los resultados de la simulación. La segmentación se puede llevar a cabo por diferentes conceptos; su resultado será siempre el mismo.
Una gama de valores de gris caracterizan las diferentes estructuras en una imagen. Diferentes principios de segmentación automática se basan en los valores de gris del pixel, región o detección de bordes.15 Estos pueden ser utilizados para las imágenes en que las estructuras anatómicas muestran una notable diferencia en los valores de gris. Sin embargo, para las imágenes obtenidas por MRN no será posible utilizar una segmentación automática, debido a que las diferencias de valores de gris no son lo eficientemente altos, producto de la propia característica de la resonancia magnética.12 Entonces, el algoritmo matemático encargado de comparar entre un valor u otro entrará en incertidumbre, lo cual provocará errores en la segmentación. Por tanto, se recomienda utilizar una segmentación semiautomática que se inicia con uno de los principios segmentación automática para la detección de grandes áreas conectadas.
La operación de umbral es uno de los procedimientos de detección automática más conocidos,3 y pertenece a los procedimientos basados en el análisis de los píxeles. Es rápida, pero no es muy precisa para imágenes de carácter homogéneo. A menudo es utilizada para segmentaciones de visión general rápida, si no se requiere una información detallada del objeto bajo observación.
El algoritmo compara cada valor de gris del pixel de la imagen obtenida y la compara con una definida por el usuario. El píxel se asigna a la estructura para que forme parte de la imagen final, si el valor de píxel está en el rango del umbral que fue predefinido por parte del operador. La aplicación en toda la imagen de este procedimiento se conoce con el nombre de umbral global, técnica que trae posibles errores que pueden a menudo conducir a una exclusión de los píxeles que pertenecen a la misma estructura. Por tanto, los mejores resultados pueden ser obtenidos mediante el uso de un umbral local, donde la imagen se separa en diferentes zonas con diferentes umbrales que son manejados por el operador, no por parte de la máquina computadora. Es necesario destacar que este método carece de aplicación para detectar pequeños cambios en una imagen, pero se puede aplicar en regiones con casi los mismos valores de gris, como los huesos.
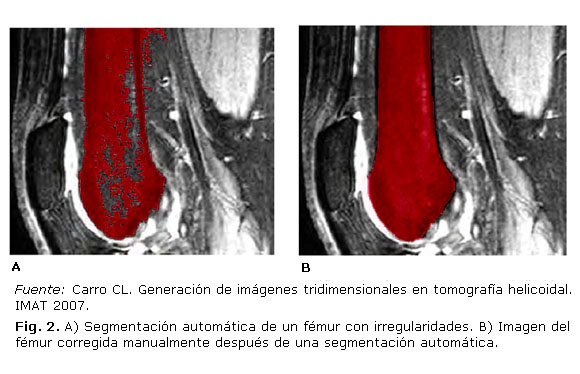
Otro método para identificar las diferentes regiones en una imagen se basa en la detección de bordes. El principio de funcionamiento de este método se fundamenta en que el algoritmo comprueba los cambios de valor de gris de una imagen mediante la comparación de dos los píxeles vecinos.16 La combinación de todos los valores de las diferencias de color gris proporciona una línea entre las partes detectadas. Se utilizan como filtros de imágenes el conocido operador de Laplace para la búsqueda de los bordes de una imagen. Al igual que con el método del umbral, el algoritmo de detección de bordes de Laplace es a veces insuficientemente sensible para una segmentación satisfactoria, de manera que se utiliza una mejora manual llevada a cabo por el operador. Un ejemplo de ello se puede observar en la figura 2 (A y B).
Mallado de las imágenes segmentadas
Antes de comenzar el mallado de los volúmenes tridimensionales es necesario un proceso previo de interpolación para analizar, en caso necesario, si todos los datos obtenidos por la TAC son suficientes. En caso negativo se procedería a generar los datos faltantes por interpolación de los ya existentes, posibilitando así obtener un volumen lo más cercano a la realidad. Luego de pasar la imagen por interpolación se genera una malla de tamaño, superficie y calidad adecuados, utilizando para ello elementos tipo tetraedros.
Uno de los métodos más empleados en el algoritmo de Watson permite obtener una "triangulación Delaunay" a través de un conjunto de puntos para cualquier región del espacio. Esta triangulación se emplea con el propósito de enlazar los puntos o vértices detectados con sus vecinos cercanos. Después de este proceso la imagen presenta algunas irregularidades generadas fundamentalmente por el proceso de captura inicial de las imágenes. Para solucionar esto es necesario someter la malla a un suavizado.
Obtención del modelo de elementos finitos
La generación del modelo de elementos finitos consiste en la determinación de los parámetros geométricos, la creación de un adecuando mallado y la especificación de las características del material. El método más habitual para la generación de la malla es la conversión directa del vóxel de la imagen a elementos hexaédricos. Las propiedades del material generalmente se especifican tomando como referencia las densidades del tejido analizado por la TAC e introduciendo estas propiedades al software, elemento a elemento para evitar errores, debido a que el tejido óseo, por ejemplo, presenta una marcada heterogeneidad en sus propiedades, y sería un error notable el especificar globalmente una determinada constante de material. El modelo de elementos finitos obtenido se observa en la figura 3.
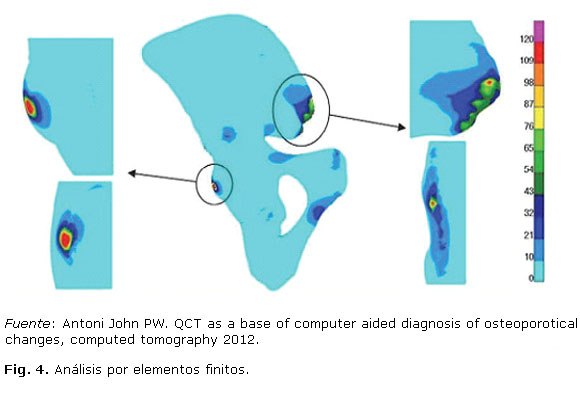
La figura 4 ilustra un análisis por elementos finitos. Se utilizó para la prueba la teoría de resistencia de Huber-Von Mises. En la imagen se observan las distribuciones de tensiones y deformaciones obtenidas por medio del software. Las distribuciones de colores determinan los distintos niveles de intensidad.
CONSIDERACIONES FINALES
El uso de las imágenes médicas permite a doctores en medicina e ingenieros obtener geometrías complejas de partes y órganos del cuerpo humano para el modelado y simulación de afecciones. La TAC es una herramienta invaluable para la detección de fracturas, malformaciones congénitas y para la detección de enfermedades del tejido óseo como la osteoporosis. Posibilita realizar diagnósticos y tratamientos sin la necesidad de acudir a métodos invasivos como la cirugía.
La fiabilidad de la TAC depende de varios factores, algunos subjetivos por parte de los operadores y, los más importantes, factores objetivos como el nivel de procesamiento de los ordenadores empleados para correr los algoritmos matemáticos para la segmentación de imágenes.
Gracias a los avances que se han obtenido en el hardware y en software de ordenadores, se ha logrado cambiar el concepto de la tomografía computarizada, y ha pasado a formar parte del uso cotidiano de tecnólogos y doctores en medicina. El método de elementos finitos es perfectamente aplicable a los procesos de modelado de funciones biológicas de los tejidos y órganos.
REFERENCIAS BIBLIOGRÁFICAS
1. Buzzi A, Suárez M. Tomografía lineal: nacimiento, gloria y ocaso de un método. Revista Argentina de Radiología. 2013;77(3):10-17.
2. Ramírez J, Castro J, Cifuentes L, Isaza J, Mariaka I, Restrepo D, eds. Análisis de la Densidad Mineral Ósea en los Fémures de Amputados Transfemorales Unilaterales mediante Comparación de Unidades Hounsfield. V Latin American Congress on Biomedical Engineering CLAIB 2011. 16-21 de mayo, 2011. La Habana, Cuba.
3. Ramírez Patiño JF, Isaza JA, Mariaka I, Vélez Zea JA. Hounsfield units as a tool for the evaluation of bone demineralization due to exoprosthesis use. Revista Facultad de Ingeniería Universidad de Antioquia. 2013(66):159-67.
4. Engelke K, Libanati C, Fuerst T, Zysset P, Genant H. Advanced CT based in vivo Methods for the Assessment of Bone Density, Structure, and Strength. Current Osteoporosis Reports. September 2013;11(3):246-255.
5. Hiroyuki Y. Local contra lateral subtraction based on bilateral symmetry of lung for reduction of false positives in computerized detection of pulmonary nodules. IEEE Transactions on Biomedical Engineering. 2004 may;51(5):778-89.
6. El-Bazl A F, Farag AA, Falk R, La Roca R. Automatic Identification of Lung Abnormalities in Chest Spiral CT Scans. International Conference on Acoustics, Speech, and Signal Processing, 2003 Proceedings (ICASSP '03); 6-10 abril 2003. p. 261-4.
7. Calzado Cantera A, Hernández-Girón I, Salvadó Artells M, Rodríguez González R. Estado actual y tendencia en el desarrollo tecnológico para la reducción de dosis en los equipos de tomografía computarizada. Radiologia. 2013;55(Suppl. 2):9-16.
8. Oñate E. Structural analysis with the finite element methods. Linear Statics. Barcelona: Ed. Springer Verlag; 2010.
9. Boccaccio A, Ballini A, Pappalettere C, Tullo D, Cantore S, Desiate A. Finite element method (FEM), mechanobiology and biomimetic scaffolds in bone tissue engineering. Int J Biol Sci. 2011;7(1):112-32.
10. Frigi Bissoli C, Gómez Ágreda C, Mitsunari Takeshita W, De Melo Castilho JC, Medici Filho E, Leonelli De Moraes ME. Importancia y aplicaciones del sistema de tomografía computarizada Cone-Beam (CBCT). Acta Odontológica Venezolana. 2013;45(4): 45-9.
11. De Carrera PF. Simulación mediante elementos finitos del comportamiento de un clavo intramedular para fracturas de tibia. [Proyecto de Fin de Carrera Ingeniería Industrial] 2011. [Consultado 23 de diciembre de 2013]. Disponible en: http://zaguan.unizar.es/TAZ/CPS/2011/5564/TAZ-PFC-2011-016.pdf
12. Diederichs G, Köhlitz T, Kornaropoulos E, Heller MO, Vollnberg B, Scheffler S. Magnetic Resonance Imaging Analysis of Rotational Alignment in Patients With Patellar Dislocations. The American Journal of Sports Medicine. 2013;41(1):51-7.
13. Li H, Wang Z. Intervertebral disc biomechanical analysis using the finite element modeling based on medical images. Computerized Medical Imaging and Graphics. 2006;30(6):363-70.
14. Cortés DE, Shapiro BL, Chin EK, Werner JS, Redenbo EF, Mannis MJ. Aplicaciones Clínicas de la Tomografía de Coherencia Óptica de Alta Resolución para el Estudio de Segmento Anterior. Vision Pan-America, The Pan-American Journal of Ophthalmology. 2013;12(1):5-10.
15. Cheung AM, Adachi JD, Hanley DA, Kendler DL, Davison KS, Josse R, et al. High-Resolution Peripheral Quantitative Computed Tomography for the Assessment of Bone Strength and Structure: A Review by the Canadian Bone Strength Working Group. Current Osteoporosis Reports. 2013:1-11.
16. Leonardi V, Vidal V, Mari J-L, Daniel M. 3D reconstruction from CT-scan volume dataset application to kidney modeling. Proceedings of the 27th Spring Conference on Computer Graphics; Slovak Republic. ACM. 2013;111-20.
17. Carro CL. Generación de imágenes tridimensionales en tomografía helicoidal. Proceso y etapas de obtención, principios básicos y aplicaciones. Instituto Médico de alta tecnología. [Proyecto de Fin de Carrera]. 2007. [Consultado 23 de diciembre de 2013]. Disponible en: http://www.unsam.edu.ar/escuelas/ciencia/alumnos/PUBLIC.2007-/(TAC)2007-CARRO CECILIA.pdf
18. Antoni John PW. QCT as a base of computer aided diagnosis of osteoporotical changes, computed tomography 2012. [Consultado 23 de diciembre de 2013]. Available from: http://www.intechopen.com/books/computed-tomography-clinical-applications/qct-as-a-base-of-computer-aided-diagnosis-of-osteoporotical-changes
Recibido: 13 de enero de 2014
Aprobado: 30 de enero de 2014
Ing. Yosbel Ángel Cisneros Hidalgo. Facultad de Electromecánica. Departamento de Ingeniería Mecánica. Universidad de Camagüey, Cuba. Correo electrónico: yosbel.cisnero@reduc.edu.cu