Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Investigaciones Biomédicas
versión On-line ISSN 1561-3011
Rev Cubana Invest Bioméd vol.36 no.4 Ciudad de la Habana oct.-dic. 2017
ARTÍCULO ORIGINAL
Ley matemática exponencial aplicada a la evaluación de la dinámica cardíaca en 18 horas
Mathematical exponential law applied to the evaluation of the cardiac dynamics in 18 hours
Catalina Correa Herrera,I Javier Rodríguez Velásquez,I Signed Esperanza Prieto Bohorquez,I Dharma Rodríguez,I Esmeralda Guzmán,I Miguel Urina,II Isabel Echeverri-Ocampo,III Farid Meléndez-Pertuz,III Rafael OyagaIII
I Grupo Insight. Centro de Investigaciones Clínica del Country. Bogotá, Colombia.
II Fundación del Caribe para la Investigación Biomédica. Universidad Simón Bolívar. Barranquilla, Colombia.
III Institución Universidad de la Costa. Barranquilla, Colombia.
RESUMEN
Introducción: la teoría de los sistemas dinámicos estudia la evolución de los sistemas. Mediante esta teoría y la geometría fractal se desarrolla una ley matemática de ayuda diagnóstica a los sistemas dinámicos cardíacos, que permite diferenciar entre normalidad y enfermedad, y la evolución entre los dos estados.
Objetivo: confirmar la capacidad diagnóstica de la ley matemática exponencial desarrollada inicialmente para dinámicas cardíacas en 21 horas, para dinámicas evaluadas en 18 horas.
Métodos: se tomaron 400 registros electrocardiográficos, 80 de dinámicas normales y 320 de dinámicas anormales. Se generó una sucesión pseudoaleatoria con el número de latidos/hora y las frecuencias máximas y mínimas cada hora; luego, se construyó el atractor de cada dinámica, para así calcular los espacios de ocupación y la dimensión fractal. Por último, se estableció el diagnóstico físico-matemático en 18 y 21 horas y se comparó con el diagnóstico clínico tomado como Gold Standard, obteniéndose valores de sensibilidad, especificidad y coeficiente Kappa.
Resultados: se encontraron valores de ocupación espacial en la rejilla Kp para normalidad entre 236 y 368 y para estados patológicos entre 22 y 189, lo que permitió diferenciar entre normalidad, enfermedad, y estados de evolución hacia la enfermedad en 18 horas. Se obtuvieron valores de sensibilidad y especificidad del 100 % y coeficiente Kappa igual a 1.
Conclusiones: la ley matemática permitió dictaminar diagnósticos reduciéndose el tiempo de evaluación a 18 horas, y se confirmó así su aplicabilidad clínica.
Palabras clave: ley; dinámica cardíaca; atractor; diagnóstico.
ABSTRACT
Introduction: dynamical systems theory aims to study the evolution of systems. With this theory and fractal geometry, it was developed a mathematical law of diagnostic utility in cardiac dynamical systems that may differentiate normality from disease and evolution between these two states.
Objective: To confirm the diagnostic capacity of the exponential mathematical law initially developed for cardiac dynamics in 21 hours, for dynamics evaluated in 18 hours.
Methods: there were taken 400 electrocardiographic records, 80 from normal dynamics and 320 from abnormal dynamics. A pseudorandom sequence was generated with the number of beats per hour and the maximum and minimum frequencies each hour; then, the attractors were built for each dynamic, in order to calculate the space occupation and the fractal dimension. Finally the physical and mathematical diagnosis in 18 and 21 hours was established, and compared to clinical diagnosis taken as Gold Standard, obtaining values of sensitivity, specificity and Kappa coefficient.
Results: there were found values for spatial occupation in the Kp grid between 236 and 368 for normal cases, and between 22 and 189 for pathological states, which allowed distinguish normality from disease and states of progression to disease in 18 hours. There were obtained values for sensitivity and specificity of 100% and a Kappa coefficient equal to 1.
Conclusions: the mathematical law allowed to stablish diagnostics by reducing the evaluation time to 18 hours confirming its clinical applicability.
Keywords: law; cardiac dynamics; attractor; diagnostic.
INTRODUCCIÓN
El objetivo de la teoría de sistemas dinámicos es analizar el estado y evolución de un sistema dado, mediante el estudio del comportamiento de sus variables en el tiempo. Uno de los primeros sistemas dinámicos estudiados fue el sistema solar.1,2 Las variables dinámicas son representadas geométricamente en un campo llamado espacio de fases, y su figura geométrica es denominada atractor. El atractor permite describir la trayectoria y tendencia evolutiva del sistema.3 En algunos casos las trayectorias geométricas son predecibles, como en el péndulo o el sistema solar. También pueden ser impredecibles o caóticas.4 Estas últimas son impredecibles y de forma geométrica irregular, por lo cual son evaluadas a la luz de la geometría fractal y el método de Box-Counting.5
Según el informe de Prioridades para la Salud Cardiovascular en las Américas de la Organización Panamericana de la Salud, la población adulta menor de 70 años tiende a tener más riesgo de padecer enfermedades cardíacas en los próximos 10 años. 6 Las enfermedades isquémicas del corazón son las principales causas de muerte en Colombia desde el año 2005 y el número de casos va en aumento.6
Por lo anterior, en el área de la cardiología se han hecho nuevas investigaciones en distintas poblaciones, con el fin de entender el comportamiento cardíaco, mediante el análisis de la variabilidad de la frecuencia cardíaca (VFC) a partir de los cambios del intervalo RR en el tiempo.7-9 Estos resultados han sido interpretados con el principio de homeostasis.10
No obstante, desde las teorías físicas y matemáticas se han realizado novedosas investigaciones con el fin de analizar la dinámica cardíaca por medio de los valores de la frecuencia cardíaca (FC) de registros electrocardiográficos continuos y/o Holter, consiguiendo así el desarrollo de metodologías predictivas y capaces de diferenciar estados de normalidad, anormalidad y en evolución hacia enfermedad.11-16 Ejemplo de esto es el desarrollo de una ley exponencial basada en la teoría de los sistemas dinámicos y geometría fractal, enunciada con el fin de analizar el comportamiento de la dinámica cardíaca durante 21 horas.11 Al observar la evolución de la dinámica cardíaca hacia la enfermedad desde un punto de vista geométrico, se observó que el tamaño del atractor cardíaco decrece progresivamente en el espacio fractal de Box Counting.12
Esta ley ha sido aplicada al estudio de los cambios de la dinámica cardíaca en pacientes con arritmias,13,14 en cuyo caso se logró confirmar su capacidad diagnóstica en pacientes con alteraciones del ritmo cardíaco, estableciéndose diferencias cuantitativas entre las distintas dinámicas.14
El objetivo de este trabajo es analizar el comportamiento de la dinámica cardíaca cuando se reduce de 21 a 18 horas la duración del estudio mediante la ley exponencial desarrollada con base en la teoría de los sistemas dinámicos y geometría fractal y confirmar su aplicación clínica.
MÉTODOS
Definiciones
Espacio de fases: Espacio de 2 o más dimensiones en el que se caracteriza geométricamente la dinámica de un sistema mediante la representación gráfica de los pares ordenados de valores correspondientes a una variable dinámica consecutiva en el tiempo.
Dimensión Fractal de Box-Counting: Se define por la ecuación 1:
En donde D corresponde a la dimensión fractal; N es el número de cuadros ocupado por un objeto en la cuadrícula de grado de partición k.
Ecuación de Box-Counting simplificada: Es obtenida a partir de la ecuación 1, aplicada a dos cuadrículas que tienen una proporción de ½ en sus dimensiones, obteniéndose de este modo la ecuación 2:
Kp es el número de cuadros ocupados por la cuadrícula más pequeña y Kg los correspondientes a la cuadrícula grande.
Ley exponencial de la dinámica caótica cardíaca: Se deriva de un despeje de la Ecuación 2 y es expresada matemáticamente de la siguiente manera (ecuación 3):
Población
Fueron seleccionados 400 registros ambulatorios y continuos en 21 horas de sujetos con edad superior a 21 años, de los cuales 80 correspondían a pacientes con diagnóstico clínico de normalidad y 320 a pacientes con diagnóstico de enfermedad cardíaca según un cardiólogo experto. Los registros se obtuvieron de bases de datos del grupo Insight.
Procedimiento
Inicialmente, se ocultaron los diagnósticos clínicos emitidos por un cardiólogo experto durante el estudio. Se tomaron los valores máximos y mínimos de las frecuencias cardíacas y el número total de latidos cada hora durante 21 y 18 horas. Con esta información se generó una sucesión pseudoaleatoria de frecuencias cardíacas mediante un algoritmo equiprobable. Después, tomando como base dicha secuencia se procedió a construir el atractor caótico graficando una frecuencia cardíaca con la consecutiva en el tiempo, en el espacio de fase, dando lugar al correspondiente atractor. Luego, se calculó la dimensión fractal mediante la Ecuación 2 para lo cual se superpusieron dos rejillas de 5 lat./min (Kp) y 10 lat./min (Kg),asimismo fueron calculados los espacios de ocupación de cada atractor en Kp y Kg.
Por medio de la Ecuación 3 se determinó el diagnostico matemático para cada registro, con base en la ley matemática exponencial, según la cual la enfermedad presenta espacios de ocupación en la rejilla Kp menores a 73; la dinámica normal presenta valores en la rejilla Kp mayores a 200 y los estados de evolución hacia la enfermedad se caracterizan por presentar espacios de ocupación entre 73 y 200. Obtenidos los diagnósticos matemáticos de las dinámicas cardíacas de 18 y 21 horas se procede a realizar la comparación con el Gold Standard.
Análisis estadístico
El diagnóstico clínico emitido por el cardiólogo experto para cada registro fue tomado como Gold-Standard para efectos de su comparación frente al diagnóstico físico-matemático en 18 y 21 horas para los registros normales y en estado agudo. Se procedió a calcular los falsos negativos, falsos positivos, verdaderos positivos y verdaderos negativos por medio de una tabla de contingencia de 2 x 2. Asimismo, se estableció el nivel de correspondencia entre el diagnóstico matemático y el diagnóstico convencional mediante el coeficiente Kappa.
Aspectos éticos
El presente estudio se acoge a los principios éticos, técnicos y científicos de la Declaración de Helsinki de la Asociación Médica Mundial. De acuerdo con la Resolución 8430 de 1993 del Ministerio de Salud de Colombia, se establece como una investigación con riesgo mínimo dado que se realizan cálculos con base en paraclínicos prescritos previamente según protocolos médicos convencionales, protegiendo la información e integridad de los sujetos.
RESULTADOS
En la tabla 1 se evidencian los diagnósticos establecidos según parámetros clínicos convencionales de algunos de los registros electrocardiográficos del estudio.
Tabla 1 . Información del diagnóstico clínico inicial de algunos
registros electrocardiográficos tomados para el estudio
| Holter No. | Indicaciones |
| 1 | Control arritmia |
| 2 | Control POS cardioversión |
| 3 | Fibrilación auricular en estudio |
| 4 | Normal |
| 5 | B AV Segundo grado Mobitz 1 |
| 6 | Normal |
| 7 | Normal |
| 8 | Taquicardia en estudio |
| 9 | Normal |
| 10 | Normal |
| 11 | ACV |
| 12 | Control médico |
| 13 | Taquicardia ventricular en estudio |
| 14 | Arritmia en estudio |
| 15 | Miocardiopatía restrictiva |
| 16 | Taquicardia en estudio |
| 17 | Normal |
| 18 | Normal |
| 19 | Accidente isquémico transitorio |
| 20 | Normal |
| 21 | Neuropatía óptica |
| 22 | Ahogo |
| 23 | Normal |
| 24 | Palpitaciones |
| 25 | Normal |
| 26 | Bloqueo AV en estudio |
| 27 | Normal |
| 28 | Normal |
| 29 | Control de arritmia |
| 30 | Dolor torácico |
| 31 | Normal |
| 32 | Estenosis aórtica severa e insuficiencia mitral moderada a severa |
| 33 | Arritmia. Pausas sinusales diurnas y nocturnas con máxima duración de 2,4 segundos |
Se encontró que las dimensiones fractales de las dinámicas cardíacas normales evaluadas en 18 horas tuvieron valores entre 0,944 y 1,909; las dinámicas con alguna enfermedad presentaron valores entre 0,761 y 1,917, con lo cual se pudo confirmar que los valores de la dimensión fractal no permiten diferenciar las dinámicas cardíacas (tabla 2).
En la rejilla Kp y Kg, las dinámicas normales evaluadas en 21 horas, presentaron espacios de ocupación entre 238 y 370, y entre 65 y 184, respectivamente. Mientras que las dinámicas con alguna patología presentaron espacios de ocupación en la rejilla Kp entre 22 y 191 y en la rejilla Kg entre 8 y 83 (tabla 2).
Asimismo, en la rejilla Kp y Kg, las dinámicas normales evaluadas en 18 horas, presentaron espacios de ocupación entre 236 y 368, y entre 67 y 183, mutuamente. En tanto que las dinámicas patológicas presentaron espacios de ocupación en la rejilla K p entre 22 y 189 y en la rejilla Kg entre 6 y 85 (tabla 2). De los resultados se observó que tanto para la dinámica cardíaca de 18 horas como para la de 21 horas los diagnósticos matemáticos coinciden.
Los resultados evidenciaron que los límites determinados para dinámicas normales y con algún padecimiento mediante la ley matemática exponencial aplicada a 21 horas, igualmente permiten realizar diagnósticos de las dinámicas cardíacas evaluadas en 18 horas, por medio de los espacios de ocupación de cada atractor en la rejilla Kp, lo cual se corrobora con el análisis estadístico en el que se obtuvo sensibilidad y especificidad del 100 % y coeficiente Kappa igual a 1, para ambos casos.
En las figuras 1, 2 y 3 se muestran los atractores de una dinámica aguda, en evolución hacia la agudización y normal, respectivamente. Se puede observar que la diferencia de tamaño es significativa entre la dinámica normal y la aguda; también, se aprecia cómo decrece el tamaño del atractor mientras se acerca a la agudización de la enfermedad.
DISCUSIÓN
Este es el primer trabajo en el que se hace una reducción del tiempo de evaluación de la ley exponencial de 21 a 18 horas en 400 registros. Se evidenció que en 18 horas es posible mediante la ley matemática diferenciar entre normalidad y anormalidad, así como estados evolutivos, lo que sirve de ayuda como herramienta diagnóstica de utilidad clínica demostrando su aplicabilidad y validez luego de evaluar su concordancia diagnóstica frente al "Gold Standard". Fue posible establecer diferencias entre dinámicas cardíacas mediante el orden matemático subyacente, al margen de consideraciones de tipo causal, obteniéndose valores de sensibilidad y especificidad de 100 %, y un coeficiente Kappa de 1.
La primera metodología que se desarrolló con base en los sistemas dinámicos, con el fin de estudiar la dinámica cardíaca por medio de los espacios de ocupación de los atractores, permitió cuantificar diferencias entre dinámicas patológicas y normales, lo cual se corroboró mediante una prueba diagnóstica lográndose valores de sensibilidad y especificidad del 100 % y coeficiente Kappa de 1 con respecto al diagnóstico clínico convencional.12 Se confirmó la capacidad diagnóstica de la metodología al analizar el comportamiento de la dinámica cardíaca de pacientes de la Unidad de Cuidados Intensivos (UCI) durante 16 horas, consiguiéndose una reducción del tiempo de evaluación, sin tener en cuenta los factores en los que se encontraba el paciente seleccionado para el estudio, ni su condición clínica.17
Las dinámicas cardíacas son susceptibles de ser estudiadas a la luz de la evaluación de señales fisiológicas; 18-20 no obstante, se han tenido diversas dificultades para lograr establecer los límites que se ajusten al diagnóstico clínico debido a la falta de un algoritmo que permita revelar información para establecer diferencia de manera adecuada y precisa entre estados normales y anormales.21 Rodríguez desarrolló una ley exponencial matemática con la cual es posible analizar cualquier dinámica cardíaca en 21 o 18 horas, considerándose únicamente los valores máximos y mínimos de las frecuencias cardíacas y el número de latidos por hora.
Esta ley se desarrolló por medio de abstracciones e inducciones con base en teorías y leyes de la física y las matemáticas, permitiéndose describir el fenómeno de forma general en el contexto del método inductivo de la física teórica moderna, lo que permite su ulterior aplicación a casos específicos. Desde este punto de vista se han desarrollado diversos diagnósticos de aplicabilidad en el ámbito médico, tal es el caso de una metodología fundamentada en la entropía proporcional, por medio de la cual se distingue normalidad, enfermedad crónica, aguda y evolución hacia enfermedad.15,22 Por medio de la ley de Zipf-Mandelbrot se creó una metodología para evaluar la dinámica cardíaca con aplicación en la UCI;23 asimismo, se logró desarrollar un método basado en la teoría de probabilidad, mediante el cual por medio de rangos es posible diferenciar dinámicas normales, con alguna enfermedad y en estados intermedios en pacientes, cursándose alteraciones del ritmo cardíaco.24-26
Con base en dicha perspectiva físico-matemática se ha logrado solucionar diferentes problemas en diversos campos de la medicina; muestra de ello, es el reciente desarrollo de una metodología predictiva de mortalidad en UCI basada en la teoría de sistemas dinámicos y de conjuntos.27 También, se ha logrado evaluar la dinámica cardíaca neonatal permitiéndose predecir el comportamiento de la dinámica cardíaca en estados de sepsis.28 Igualmente, se han realizado predicciones en el área de la morfometría arterial y celular,29,30 en la hematología,31 en la predicción de linfocitos T CD4,32 en temas preponderantes como la predicción de epidemias33,34 y en la inmunología.35
Agradecimientos
A la Universidad de la Costa, a la Fundación del Caribe para la Investigación Biomédica y a la Universidad Simón Bolívar, por su apoyo a nuestras investigaciones. Extendemos nuestros agradecimientos al Centro de Investigaciones de la Clínica del Country, en especial a las doctoras del Centro de Investigaciones Adriana Lizbeth Ortiz, epidemióloga, y Silvia Ortiz, enfermera jefe, a la enfermera Sandra Rodríguez y a los doctores Tito Tulio Roa, Director de Educación Médica, Jorge Alberto Ospina, Director Médico, y Alfonso Correa, Director del Centro de Investigaciones, por el apoyo constante a nuestro grupo de investigación.
Apoyo financiero
Clínica del Country de Bogotá, Fundación del Caribe para la Investigación Biomédica, Universidad Simón Bolívar y Universidad de la Costa.
Conflicto de intereses
Los autores declaran no tener conflictos de intereses.
REFERENCIAS BIBLIOGRÁFICAS
1. Feynman R, Leighton R, Sands M. Leyes de Newton de la Dinámica. Wilmington: Addison-Wesley Iberoamericana, S.A. 1987;(3):9-14.
2. Devaney R. A first course in chaotic dynamical systems theory and experiments. Reading Mass: Addison-Wesley; 1992.
3. Peitgen H, Jurgens H, Saupe D. Chaos and fractals; new frontiers of science. New York: Springer; 1992.
4. Mandelbrot B. The fractal geometry of nature. Barcelona: Tusquets Eds. S.A.; 2000. p. 341-8.
5. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? En: Los objetos fractales. Barcelona: Tusquets Eds. S.A.; 2000. p. 27-50.
6. Pan American Health Organization. Regional Consultation Priorities for Cardiovascular Health in the Americas. Key Messages for Policymakers; 2011.
7. Bayés A. Muerte súbita. Revista Española de cardiología. 2012;65(11):1039-52.
8. Nolan J, Batin PD, Andrews R, Lindsay SJ, Brooksby P, Mullen M, et al. Prospective study of heart rate variability and mortality in chronic heart failure: results of the United Kingdom Heart Failure Evaluation and Assessment of Risk Trial (UK - heart). Circulation. 1998;98:1510-6.
9. Wolf M, Varigos G, Hunt D, Sluman J. Sinus arrhythmia in acute myocardial infarction. Med J Aus. 1978;(2):52-3.
10. Goldberger A, Rigney DR, West B. Caos y fractales en la fisiología humana. Investigación y ciencia. 1990;(163):32-8.
11. Rodríguez J. Mathematical law of chaotic cardiac dynamic: Predictions of clinic application. J Med Med Sci. 2011;2(8):1050-9.
12. Rodríguez J, Prieto S, Bernal P, Soracipa Y, Salazar G, Isaza D, et al. Nueva metodología de ayuda diagnóstica de la dinámica geométrica cardíaca. Dinámica cardíaca caótica del Holter. Rev Acad Colomb Cienc. 2011;35(134):5-12.
13. Rodríguez J, Prieto S, Domínguez D, Correa C, Melo M, Pardo J, et al. Application of the chaotic power law to cardiac dynamics in patients with arrhythmias. Rev Fac Med. 2014;62(4):539-46.
14. Rodríguez J, Prieto S, Correa C, Soracipa Y, Cardona DM, Prieto I, et al. Ley matemática para evaluación de la dinámica cardíaca: aplicación en el diagnóstico de arritmias. Rev Cienc Salud. 2015;13(3):369-81.
15. Rodríguez J, Prieto S, Domínguez D, Melo M, Mendoza F, Correa C, et al. Mathematical-physical prediction of cardiac dynamics using the proportional entropy of dynamic systems. J Med Med Sci. 2013;4(8):370-81.
16. Rodríguez J, Prieto S, Correa C, Oliveros H, Soracipa Y, Méndez L, et al. Diagnóstico de la dinámica cardiaca durante 16 horas desde los sistemas dinámicos aplicable en UCI. Revista de la Universidad Industrial de Santander. 2017 [citado 12 agosto 2017];49(1). Disponible en: http://www.redalyc.org/jatsRepo/3438/343850079008/html/index.html
17. Rodríguez J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU): Physical and mathematical mortality predictions on ICU. J Med Med Sci. 2015;6(8):209-20.
18. Soares-Miranda L, Sattelmair J, Chaves P, Duncan G, Siscovick D, Stein P, et al. Physical Activity and Heart Rate Variability in Older Adults: The Cardiovascular Health Study. Circulation. 2014 May 27;129(21):2100-10.
19. Walleczek J. Nonlinear Dynamics, Self-Organization, and Biomedicine. Cambridge, U.K.: Univ Press; 1999.
20. Goldberger A. Heartbeats, hormones, and Health - Is variability the spice of life? American Journal of Respiratory and Critical Care Medicine. 2001;163(6):1289-90.
21. Goldberger AL, Amaral L, Hausdorff J, Ivanov P, Peng CK, Stanley H, et al. Fractal dynamics in physiology: Alterations with disease and aging. Proc Natl Acad Sci USA. 2002 Feb 19;99(Suppl 1):2466-72.
22. Rodríguez J, Prieto S, Mendoza F, Velásquez N. Evaluación físico matemática de arritmias cardíacas con tratamiento terapéutico de metoprolol a partir de las proporciones de la entropía. Rev UDCA Act & Div Cient. 2015 Jul-Dic;18(2):301-10.
23. Rodríguez J, Prieto S, Correa C, Mendoza F, Weisz G, Soracipa M, et al. Physical mathematical evaluation of the cardiac dynamic applying the Zipf - Mandelbrot law. Journal of Modern of Physics. Oct 2015;6(13):1881-8.
24. Rodríguez J, Correa C, Melo M, Domínguez D, Prieto S, Cardona DM, et al. Chaotic cardiac law: Developing predictions of clinical application. J Med Med Sci. 2013;4(2):79-84.
25. Rodríguez-Velásquez J, Prieto S, Bautista J, Correa C, López-García F, Valero L, et al. Evaluación de arritmias con base en el método de ayuda diagnóstica de la dinámica cardíaca basado en la teoría de la probabilidad. Arch Med (Manizales). 2015;15(1):33-45.
26. Rodríguez J, Prieto S, Bernal P, Izasa D, Salazar G, Correa C, et al. Entropía proporcional aplicada a la evolución de la dinámica cardíaca. Predicciones de aplicación clínica. En: Rodríguez LG, Coordinador. La emergencia de los enfoques de la complejidad en América Latina: desafíos, contribuciones y compromisos para abordar los problemas complejos del siglo XXI. Tomo 1. Buenos Aires: Comunidad Editora Latinoamericana; 2015. p. 315-44.
27. Rodríguez J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU): Physical and mathematical mortality predictions on ICU. J Med Med Sci. 2015; 6(8):209-20.
28. Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, Aguirre G, et al. Physical-mathematical diagnosis of cardiac dynamic on neonatal sepsis: predictions of clinical application. J Med Med Sci. 2014;5(5):102-8.
29. Prieto S, Rodríguez J, Correa C, Soracipa Y. Diagnosis of cervical cells based on fractal and Euclidian geometrical measurements: Intrinsic Geometric Cellular Organization. BMC Medical Physics. 2014,14(2):1-9.
30. Velásquez J, Prieto S, Correa C, Dominguez D, Cardona DM, Melo M, et al. Geometrical nuclear diagnosis and total paths of cervical cell evolution from normality to cancer. Journal of Cancer Research and Therapeutics. 2015;11(Issue 1):98-104.
31. Correa C, Rodríguez J, Prieto S, Álvarez L, Ospino B, Munévar A, et al. Geometric diagnosis of erythrocyte morphophysiology: Geometric diagnosis of erythrocyte. J Med Med Sci. 2012;3(11):715-20.
32. Rodríguez J, Prieto S, Correa C, Pérez C, Mora J, Bravo J, et al. Predictions of CD4 lymphocytes' count in HIV patients from complete blood count. BMC Medical Physics. 2013;13:3.
33. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Pública. 2010;27(3):211-8.
34. Rodríguez J, Correa C. Predicción temporal de la epidemia de dengue en Colombia: Dinámica probabilista de la epidemia. Rev Salud Pública. 2009;11(3):443-53.
35. Rodríguez J, Bernal P, Prieto P, Correa C, Álvarez L, Pinilla L, et al. Predicción de unión de péptidos de Plasmodium falciparum al HLA clase II. Probabilidad, combinatoria y entropía aplicadas a las proteínas MSP-5 y MSP-6. Archivos de alergia e inmunología clínica. 2013;44(1):7-14.
Recibido: 25 de diciembre de 2016.
Aprobado: 30 de enero de 2017.
Javier Rodríguez Velásquez. Carretera 79B N° 51-16 Sur. Int. 5. Apto. 102, Barrio Kennedy, Bogotá D.C., Colombia.
Correo electrónico: grupoinsight2025@yahoo.es
 Todo el contenido de esta revista, excepto dónde está identificado, está bajo una Licencia Creative Commons
Todo el contenido de esta revista, excepto dónde está identificado, está bajo una Licencia Creative Commons













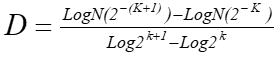 Ecuación 1
Ecuación 1 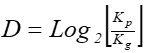 Ecuación 2
Ecuación 2 