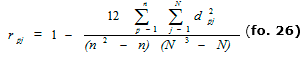Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Educación Médica Superior
versión On-line ISSN 1561-2902
Educ Med Super vol.30 no.1 Ciudad de la Habana ene.-mar. 2016
ARTÍCULO ORIGINAL
Propuesta didáctica para perfeccionar el proceso de enseñanza-aprendizaje de la Matemática, en la formación de residentes en Ciencias Básicas Biomédicas
Proposal didactics to perfect the teaching process-learning of the Mathematics, in the formation of residents in Biomedical Basic Sciences
Dr. C. Miguel Angel González Rangel, Dra. Rebeca Mendoza Taño, Dra. Roxana Mendoza Taño, MSc. Lourdes García Bacallao, MSc. Yelamy Travieso González
Instituto de Ciencias Básicas y preclínicas Victoria de Girón. La Habana, Cuba.
RESUMEN
La propuesta didáctica, es el primer trabajo en Cuba donde se aplicó la Teoría General de Sistema para estructurar el proceso de enseñanza-aprendizaje de la Matemática, en la formación de residentes de Ciencias Básicas Biomédicas, utilizando la resolución de clases de problemas variando los instrumentos. Aquí los problemas matemáticos con enfoque biomédico, sirvieron para motivar, enriquecer y estructurar los contenidos. La propuesta se está aplicando desde el curso 2012-2013 y ha contribuido a la elevación de la motivación y la aplicación integrada de los conocimientos, métodos, modos de actuación y la posibilidad de que los residentes revelaran relaciones interdisciplinarias. Su pertinencia se evaluó a partir de la utilización del método prospectivo conexo en dictámenes de especialistas o expertos y de acuerdo con los rangos definidos se probó la existencia de concordancia entre los criterios emitidos, lo cual indicó que realizaron un análisis racional de la propuesta, garante de la objetividad del resultado.
Palabras clave: teoría General de Sistema; Estructura de Conocimiento; Resolución de Clases de Problemas variando los instrumentos; Ciencias Básicas Biomédicas.
ABSTRACT
The didactic proposal, is the first work in Cuba, where the Focus of System was applied to structure the process of teaching-learning of the Mathematics in the formation of residents of Biomedical Basic Sciences, using the resolution of classes of problems varying the instruments; here the mathematical problems, with biomedical focus, were good to motivate, to enrich and to structure the contents. The proposal is applying from the course 2012-2013 and it has contributed to the elevation of the motivation and the integrated application of the knowledge, methods, performance ways and the possibility that the residents revealed interdisciplinary relationships. Their relevancy was evaluated starting from the use of the related prospective method in specialists' verdicts or experts and in accordance with the defined ranges the existence of agreement was proven among the emitted approaches, that which indicates that they carried out a rational analysis of the proposal, guarantor of the objectivity of the result.
Key words: General theory of System; Structure of Knowledge; Resolution of Classes of Problems varying the instruments; Biomedical Basic Sciences.
INTRODUCCIÓN
El vertiginoso desarrollo de la Ciencia y la Técnica ha traído entre otras consecuencias, la interrelación cada día más frecuente entre especialistas de distintas ramas del saber humano, y por lo tanto, la necesidad de un lenguaje común para el entendimiento entre ellos. La Matemática, conjuntamente con la Estadística, las Probabilidades y las Ciencias de la Computación y la Información han ido ocupando un lugar cada vez más significativo en el ámbito laboral e investigativo de los profesionales de la salud, por citar una de las ramas donde este fenómeno se manifiesta.
Sin embargo, los profesionales de la salud que ingresan a la formación como residentes en las Ciencias Básicas Biomédicas, en su mayoría han estado desvinculados del estudio sistemático de la Matemática, lo que ha creado en ellos un rechazo a esta disciplina y en especial fomentan la falsa concepción, que para ser un profesional de la salud, no hace falta saber Matemática.
Por otra parte, no es exagerado afirmar que en los programas tradicionales de los diferentes niveles de educación, incluyendo el de Matemática para residentes, se revela la intención central de pertrechar al estudiante de conocimientos imprescindibles para seguir adelante.
En la última década del siglo XX e inicios del siglo XXI, el Grupo ß de Educación Matemática, dirigido por la Dra. C. H. Hernández, asesora del ministro de Educación Superior de Cuba, aglutinó a un grupo de profesores universitarios para investigar en torno a los problemas que existían en el proceso de enseñanza–aprendizaje (PEA) de la Matemática y en particular, los problemas de la solidez del conocimiento, la forma de organización de los contenidos en los programas y las dificultades con la resolución de problemas, considerando como posible alternativa de solución a estas problemáticas la utilización en el proceso de enseñanza aprendizaje (PEA) de la Matemática de la Teoría General de Sistema y en particular de la estructuración sistémica del conocimiento.
En este proceso investigativo, se obtuvieron resultados muy interesantes que fueron socializados en congresos nacionales e internacionales de Matemática, congresos internacionales de Pedagogía, Educación Superior y congresos internacionales de Didáctica de la Ciencias e introducidos en diferentes programas de Matemática en el Sistema Nacional de Educación, las carreras de Ingeniería, Arquitectura y de las carreras de Licenciatura en Matemática del Ministerio de Educación Superior y sirvieron como tesis doctorales de varios de los miembros del Grupo ß.1-6
La característica principal de los aportes presentados en las referidas tesis doctorales representó, con respecto a la forma tradicional, concebir el PEA de la Matemática con un salto cualitativamente superior en el tratamiento metodológico de los contenidos y la posibilidad de su asimilación sólida y eficiente.
El objetivo de este estudio es presentar una propuesta didáctica basada en la utilización del enfoque sistémico en el PEA de la Matemática de la formación de residentes de Ciencias Básicas Biomédicas.
MÉTODOS
En la concepción de la propuesta didáctica se utilizaron, sobre la base del método dialéctico materialista, diversos métodos: el método de análisis-síntesis se utilizó para precisar los presupuestos teóricos de la propuesta, a partir de la sistematización del conocimiento científico relacionado con el objeto de investigación, el método histórico- lógico para hacer un análisis del desarrollo del objeto de investigación y revelar su lógica interna, el método sistémico para estudiar cada uno de los componentes del objeto de investigación como un proceso, haciendo énfasis en la estructuración sistémica del contenido a partir de la utilización de la estructura de conocimiento conocida como resolución de clases de problemas variando los instrumentos, 3,6 aquí los problemas con enfoque biomédico se convirtieron en objeto de enseñanza aprendizaje y fueron utilizados no solo como medio para desarrollar habilidades, sino como herramientas para enriquecer y estructurar el sistema de conceptos e instrumentos necesarios para resolver nuevos problemas. Asimismo, se usó el método de modelación en el diseño de la propuesta didáctica y de cada uno de sus elementos componentes. Por último, en la valoración de la pertinencia de la propuesta didáctica y de su contribución al perfeccionamiento del PEA de la Matemática para residentes de las Ciencias Básicas Biomédicas se utilizó el método prospectivo conexo en dictámenes de peritos, especialistas o expertos.7
Es bueno destacar que los autores para lograr la correcta valoración de la propuesta didáctica por parte de los referidos especialistas, desde el inicio del curso 2014-2015 se realizaron talleres para la socialización de la propuesta didáctica. En general, se trabajó con un total de 11 especialistas o expertos. De ellos 11 son cuadros o funcionarios con más de 10 años de experiencia, como docentes universitarios: Dr.C.P (5), Dr.C.M (2), MSc. (4), Profesores Titulares (5) y Profesores Auxiliares (6).
En este trabajo se consideran especialistas a aquellos profesionales que pueden utilizar la propuesta didáctica en su desempeño profesional, profesores que imparten docencia en la formación de profesionales de la salud, en la formación de licenciados en Matemática, Física, Química, Biología e Informática, con un alto nivel científico-pedagógico.
A dichos especialistas, se les aplicó el cuestionario que aparece en el cuadro 1, para conocer sus criterios y posteriormente valorar la factibilidad de la propuesta didáctica. Estos evaluaron los fundamentos teóricos, elementos que conforman la propuesta didáctica y su posible contribución al perfeccionamiento del PEA de la Matemática.
RESULTADOS
El análisis realizado por los autores de los fundamentos filosóficos, epistemológicos y psicológicos de las concepciones acerca del aprendizaje permitió concluir que las tesis fundamentales del Materialismo dialéctico e histórico brindan un enfoque metodológico suficiente para introducir transformaciones en el PEA de la Matemática en la formación de residentes en Ciencias Básicas Biomédicas. Asimismo, se consideró que la Teoría Marxista-Leninista del Conocimiento y los aportes del Enfoque Histórico-Cultural de Vigotsky y sus seguidores brindan el marco teórico adecuado para enfrentar las transformaciones de dicho proceso. Se asume además, la necesidad de que el estudiante tenga un conocimiento bien estructurado, para que acceda a él en el menor tiempo posible, al recuperarlo, expresarlo o aplicarlo en cualquier situación.6
En este sentido se asume que estructurar el conocimiento significa: lograr que los estudiantes organicen (o reorganicen) internamente dicho conocimiento, a partir de revelar los nexos y relaciones entre sus elementos componentes.6
Para lograr esta organización, es necesario que los profesores reconozcan a sus estudiantes como centro de esta actividad, ya que no se trata de darles una aparente organización, sino que él mismo sea capaz de buscar esos nexos y relaciones y en función de eso es que se debe planificar todo el trabajo.
Como se declaró, en la Educación Superior en Cuba, se han utilizado diferentes estructuras de conocimiento, para organizar los contenidos en los programas de estudio. Se destaca el uso de las Invariantes, las Células Generadoras, los Nodos Cognitivos, la Resolución de Clases de Problemas variando los Instrumentos, como las usadas con más frecuencia y, en menor escala, las Reglas y Unidades.6
Lo común de estos enfoques está, en que orientan a la búsqueda de las regularidades, por alcanzar un elevado grado de generalización en poco tiempo, por la no particularización de los conocimientos, por el estudio de sus conexiones y su integridad, por considerar los conceptos, relaciones y procedimientos particulares como manifestaciones de otros, los cuales una vez asimilados, se reflejarán fenoménicamente como resultado de la aplicación del principio general con determinadas variaciones.
La característica principal de cualquiera de ellos, es que con respecto a la forma tradicional de enseñanza, representan un salto cualitativamente superior de tratamiento metodológico y de posibilidad de una asimilación eficiente y sólida de los contenidos. Este tipo de orientación libera al que aprende de la necesidad de estudiar cada fenómeno particular de la rama dada; ... el paso al nuevo modo de almacenamiento de la información, o sea, en lugar de abordar una multitud de hechos particulares, analizados a través de métodos también particulares, se da un método único de análisis con el cual se abordan algunos casos representativos del conjunto, en número preciso, necesario para la asimilación de este método para que posteriormente el estudiante construya de forma independiente, a partir de él, cualquier fenómeno del sistema dado.
Sobre la base de estos presupuestos teóricos, se introduce en el PEA de la Matemática para residentes de las Ciencias Básicas Biomédicas la referida propuesta didáctica, donde se concretan armónicamente las siguientes ideas esenciales:
- Asumir una concepción del diagnóstico integral de la personalidad.
- Reformular los objetivos en los niveles jerárquicos: unidad, subunidad y clase; en términos de aprendizaje, teniendo en cuenta los aspectos: instructivo, educativo y desarrollador. En particular, se considera el aprendizaje de la resolución de problemas matemáticos con enfoque biomédico, como objeto de enseñanza-aprendizaje.
- Estructurar sistémicamente el PEA de los contenidos matemáticos a partir de la resolución de clases de problemas, variando los instrumentos.3,6
- Utilizar métodos y formas de enseñanza que potencian la actividad productiva y creativa de los estudiantes. En particular, se introduce, la resolución de problemas en grupos pequeños ―trabajo en equipos, realización de tareas docentes― trabajos investigativos cuyos resultados se discuten en seminarios.
- Asumir el control y la evaluación como un proceso sistémico, continuo y participativo.
Esta propuesta didáctica se está aplicando en el desarrollo del Programa de la asignatura Matemática en la formación de residentes de Ciencias Básicas Biomédicas en la Facultad de Ciencias Médicas I.C.B.P “Victoria de Girón” desde el curso 2012-2013. Para su introducción, se realizó un estudio detallado de los resultados de la exploración inicial realizada como parte del diagnóstico integral concebido en el colectivo de profesores y se analizaron los contenidos matemáticos que aparecen en el programa de la asignatura. Se valoraron las posibles situaciones teóricas y prácticas a las que deberán enfrentarse los residentes al culminar su formación. A partir de este análisis se asumió como objetivo general de la asignatura:
Resolver problemas matemáticos con enfoque biomédico, con un nivel medio de dificultad donde se apliquen de forma integrada las operaciones con números reales y sus subconjuntos, las propiedades de las funciones reales en una variable, el cálculo diferencial e integral y las ecuaciones diferenciales.
Seguidamente, se realizó un análisis del contenido del programa y se estructuró el PEA de la Matemática a partir de la resolución de clases de problemas variando los instrumentos.3,6
En este punto de la propuesta didáctica se concentran las acciones relacionadas con la estructuración sistémica de los contenidos. En particular, se realizaron las siguientes acciones de carácter metodológico:
I. Determinar los conocimientos o instrumentos que provee el contenido de la asignatura para la resolución de problemas con enfoque biomédico relativos a él.
II. Determinar todos los problemas que pueden ser considerados como aplicaciones inmediatas del contenido objeto de estudio, siempre que estos no rebasen los límites establecidos en los objetivos del programa.
III. Agrupar dichos problemas en el menor número de clases de problemas posibles, considerando la exigencia del objeto de estudio del problema y no por el instrumento con que se resuelve.
IV. Seleccionar los problemas que serán utilizados para enriquecer el sistema de conocimientos o de instrumentos.6
V. Organizar los contenidos de forma tal que se lleve de frente la resolución de las distintas clases de problemas con enfoque biomédico y en cada tema permanezca invariable el sistema de instrumentos a utilizar.
Se destaca que los problemas con enfoque biomédico constituyen el punto inicial de discusión para demostrar la insuficiencia del contenido. Asimismo, facilitan la reestructuración de los contenidos alrededor de estas clases de problemas, que se irán ampliando en la medida que se enriquecen los conocimientos o instrumentos.
Esta forma de organización permite mostrar al estudiante la secuencia lógica de presentación de las partes de la asignatura como un sistema, ya que se revela y fundamenta su lógica, lo que facilita la presentación del objeto de estudio a partir de las ideas esenciales que lo constituyen, el mecanismo que permite explicar su origen y su desarrollo, con las diferentes formas particulares de su existencia como expresión de lo general.
Al analizar los problemas que se resolverían, en función de los contenidos, se revelaron las clases de problemas siguientes: problemas de cálculo, problemas de aproximación, problemas de graficación.
Por ejemplo, al comenzar el estudio de las funciones y sus propiedades, se presentaron problemas como los siguientes:
1. Se estudiaron los efectos nutricionales sobre ratas que fueron alimentadas con una dieta de alto contenido de proteína. La proteína consistía en levadura de harina de maíz. Variando el porcentaje p de la levadura en la mezcla de proteína se estimó que la masa promedio ganado en gramos de una rata en un período fue f(p) = + 2 p + 20 (fo.1). Calcule la masa máxima alcanzada por la rata.
2. Una de las causas por lo que una persona tose puede ser la existencia de un objeto extraño en su tráquea. La velocidad de la tos depende del tamaño del objeto. Supongamos que una persona tiene una tráquea cuyo radio es 20 mm. Si un objeto extraño tiene un radio r (en milímetros), entonces la velocidad (V) en (mm/s), necesaria para eliminar el objeto, está dada por: V(r)=k (20 r2- r3): 0 ≤ r ≤ 20 y k (fo. 2) es una constante positiva. Calcula para qué tamaño del objeto se necesita la velocidad máxima para removerlo.
Estos problemas están en la clase de problemas de cálculo. La solución del primer problema se encontraría fácilmente al calcular el vértice de la parábola y su segunda coordenada sería el valor máximo de la masa alcanzada por la rata.
Sin embargo, el segundo, aunque pertenece a la misma clase de problemas, los conocimientos e instrumentos estudiados sobre funciones no son suficientes para resolverlo. Aquí se produce un conflicto cognitivo… es necesario enriquecer el sistema de conocimientos o de instrumentos, se necesita un nuevo conocimiento o instrumento: el cálculo diferencial.
Por tanto, el segundo problema sirvió para motivar la necesidad de ampliar el sistema de contenidos, para después poder resolver nuevos problemas. Los problemas son modelados a partir de la utilización de datos y situaciones reales y se discuten con un enfoque interdisciplinar. La interdisciplinariedad es una estrategia didáctica8 que prepara al estudiante para realizar transferencias de contenidos que les permite solucionar holísticamente los problemas. En particular, para el caso de los residentes los prepara para enfrentar la solución de problemas relacionados con su futuro desempeño profesional.
La utilización de la interdisciplinariedad contribuye al logro de una cultura integral y a la formación de una concepción científica del mundo en los residentes, desarrollar en ellos un pensamiento humanista, científico y creador que les permita adaptarse a los cambios de contextos y abordar problemas de interés social.
Otro elemento esencial de la propuesta didáctica es la utilización de métodos y formas de enseñanza que potencian la actividad productiva y creativa de los estudiantes. En particular, se organizó la resolución en equipos, de problemas biomédicos y de otras ciencias, haciendo énfasis en la argumentación de los pasos a dar y el porqué de las acciones que realizan para llegar a la solución, se elaboraron resúmenes que facilitaron una parte significativa del proceso de orientación, y reorganización de sus conocimientos, lo que disminuyó el tiempo de los bloqueos y facilitó la recuperación efectiva de la información.
A continuación se muestran ejemplos de problemas matemáticos con enfoque biomédico que fueron resueltos por los residentes en cada uno de los temas que forman parte del programa:
- Un farmacéutico debe preparar 15 mL de unas gotas para los ojos para un paciente con glaucoma. La solución de las gotas debe contener 2 % de un ingrediente activo, pero el farmacéutico solo tiene una solución al 10 % y otra al 1 % en su almacén. ¿Qué cantidad de cada tipo de solución debe usar para preparar la receta?
- Un paciente con cáncer recibir´a terapia mediante f´armacos y radiaci´on. Cada cent´ımetro c´ubico de medicamento que se usar´a contiene 200 unidades curativas, y cada minuto de exposici´on a la radiaci´on proporciona 300 unidades curativas. El paciente requiere 2400 unidades curativas. Si d cent´ımetros c´ubicos de la droga y r minutos de radiaci´on son administrados, determine la funci´on lineal que relaciona d y r. Grafique e intérprete los resultados.
- En una prueba para metabolismo de az´ucar en la sangre, llevada a cabo en un intervalo de tiempo, la cantidad de az´ucar encontrada est´a dada por A(t) = 3,9 + 0,2t – 0,1t2, (fo. 3) donde t es el tiempo medido en horas. Grafique la funci´on y obtenga, a partir de ella, informaci´on relevante del problema (crecimiento, decrecimiento, ceros, etcétera).
- Una bacteria estomacal debe ser tratada con un determinado tratamiento antibi´otico antes que estén presentes 10000 de ellas en el organismo, de lo contrario el tratamiento sugerido es otro. Si se sabe que su n´umero se incrementa a raz´on del 5 % cada hora y que al inicio estaban presentes 400 bacterias, determine el n´umero de bacterias N(t) presentes después de t horas. ¿De cuánto tiempo se dispone antes de cambiar el tratamiento?
- Un paciente en reposo inspira y expira 0,5 litros de aire cada 4 segundos. Al final de una expiración, le quedan todavía 2,25 litros de aire de reserva en los pulmones. Después de t segundos de iniciado el proceso, el volumen de aire en los pulmones (en litros), en función del tiempo es: V (t) = 2,5 – 0,25 cos (pt/2) (fo. 4)
a) Grafique la funci´on volumen.
b) ¿En qué instante el volumen es máximo? ¿Mínimo?
c) ¿Cuál es el valor del volumen máximo y mínimo?
- Los psic´ologos consideran que cuando se pide a una persona que recuerde un conjunto de eventos, el n´umero de hechos recordados despu´es de t minutos est´a dado por una funci´on de la forma Q(t) = A(1 − e−kt), (fo. 5) donde k es una constante positiva y A es el n´umero total de hechos importantes presentes en la memoria de la persona. ¿Qu´e ocurre a la funci´on Q cuando t crece sin l´ımite? Explique este comportamiento en t´erminos prácticos.
- Determine la virulencia de una bacteria en una escala de 0 al 50 (V). Si se conoce que la ecuación: ,(fo. 6) donde t es el tiempo (en horas) transcurridas desde que comienza en estudio (t= 0).
Además, se orientaron tareas docentes que incluían la realización de trabajos investigativos, sobre la aplicación de los contenidos matemáticos, en las Ciencias Básicas Biomédicas, resultados que se discutieron en los seminarios. En general, las tareas docentes se fueron evaluando de forma sistemática, continua y participativa.
Es significativo destacar, la importancia que tuvo la introducción de los seminarios. En estos, se discutieron trabajos muy interesantes relacionados con las aplicaciones de los contenidos matemáticos en la solución de problemas con enfoque biomédico, este modo de proceder contribuyó a que los residentes se familiarizaran con los conocimientos y métodos de la ciencia y desarrollaran habilidades profesionales asociadas a su futura profesión.
Por citar un ejemplo, uno de los equipos discutió la aplicación de los contenidos matemáticos relativos a la asignatura en la solución de un problema en el área de la Farmacología y su utilización en especialidades como la Anestesiología y Reanimación el que se presenta a continuación. Es muy importante destacar que el autor principal del artículo participó en el seminario.
¿Cuánto debe disminuir la velocidad de infusión con respecto al cálculo inicial? Para dar respuesta a este problema se partió enfocando el análisis en ¿qué tanto por ciento (%) se debería disminuir progresivamente la dosis?; de esta manera se estableció una relación entre la dosis en curso (Da) y la precedente (Db), por lo tanto (Db = Da - Da%). 9 (fo. 7)
Los residentes explicaron que para determinar el porcentaje de decrecimiento de la dosis Da (Da %) tuvo en cuenta, lo que se denomina "la función de decrecimiento exponencial, M(t) = M0e-(t/r) ",(fo. 8) la cual es en la práctica la ecuación de decrecimiento más utilizada, siendo M el valor de la magnitud (Vinf = Db) (fo. 9) a perfundir yM0 (Da) el valor inicial de la magnitud cuyo decrecimiento exponencial se está estudiando en la unidad de tiempo t, y r la constante de ritmo temporal de decrecimiento.
Se centró el análisis en el comportamiento exponencial del decrecimiento y así en la función o expresión exponencial y = f(x) = ex (fo. 10) (e es el número de Euler) para su inclusión en el ajuste del % de decrecimiento.
Asimismo, revelaron que la función exponencial ex es utilizada para modelar una relación en la cual un cambio constante de la variable independiente (x) proporciona el mismo cambio proporcional (Ej. porcentaje de crecimiento o decrecimiento) en la variable dependiente. La función exponencial es utilizada en Física, Química, Matemáticas, Procesos Biológicos, etcétera.
Además, el número de Euler (e ≈ 2.72) trasciende a la descripción del comportamiento de acontecimientos físicos regidos por leyes sencillas, entre los que se incluye la velocidad de vaciado de un depósito de agua, lo cual guarda relación con la teoría del modelo monocompartimental.
El exponente x se asumió como el límite de la sucesión f(x) = (1 + 1/n)n, (fo. 11) por lo que x = e, entonces ee. Al tenerse en cuenta lo anteriormente expuesto se propuso la siguiente hipótesis. Hipótesis de cálculo de ajuste de Vinf (t):
Se analizó una variante de cálculo de decrecimiento, y se incluyó el factor tiempo (t) a la expresión matemática, y se asumió que para el exponente e, representado por la expresión f(x) = (1 + 1/n)n, n = t; t (fo. 12) pertenece a los números naturales.
Por lo tanto:
Vinf (tn) = Vinf (tn-1) - [(Vinf (tn-1) x e(1 + 1/t)t)/100] , para t > 0. (fo. 13)
Vinf (tn) representa la velocidad a la que se debe infundir en el intervalo de tiempo en curso (tn), y Vinf (tn-1) es la velocidad de infusión que se aplicó en tn-1, el intervalo de tiempo transcurrido hasta tn (t1, t 2, t3, t4 ….t(n-1), tn).
t = tiempo en minutos (min), siendo: t1 = 30 min; t2 = 60 min; t3 = 90 min; t4 = 120 min; t5 = 150 min; t6 = 180 min.
Esta fórmula para la clínica práctica puede simplificarse a:
Vinf (tn) = Vinf (tn-1) x 0.85. (fo. 14)
Se determinó que la variación de la Vinf (t) fuera cada 30 minutos. Que el mantenimiento invariable de la Vinf (t n) de midazolam según los cálculos establecidos para la TIVA manual (modelo monocompartimental) produce el incremento de la Cp, siendo estadísticamente significativas las diferencias con respecto al modelo ideal.
Que el decrecimiento de la Vinf (tn) mediante la variante de cálculo Vinf (tn) = Vinf (t n-1) x (fo. 15) 0,85 cuando se realizó el decrecimiento durante las primeras 3 horas y al sostenerse posteriormente constante la Vinf (tn), posibilita una mejor estabilidad de la Cp, según las simulaciones realizadas empleando el modelo de Greenblatt, y resultaron sus diferencias estadísticamente no significativas con respecto al modelo ideal por un período de 6 horas.
Otro de los equipos, se refirió a la aplicación de la Matemática en modelos de problemas epidemiológicos.
En particular, se destacó que un problema importante de biología y medicina trata de la ocurrencia, propagación y control de una enfermedad contagiosa; esto es, una enfermedad que puede transmitirse de un individuo a otros.
La inmunoepidemiología estudia este problema, y si un porcentaje grande no común de una población adquiere la enfermedad, se dice que hay una epidemia. Un modelo matemático sencillo para la propagación de una enfermedad es:
, (1) (fo. 16)
Donde Pi es el número de individuos infectados en el tiempo t, P0 el número de individuos infectados en el tiempo t0y P es el número total de la población. La solución a la ecuación diferencial (1) se obtiene por separación de variables, dando como solución:
(2) (fo. 17)
Así, el modelo formado por (1) y (2) describe la propagación de una enfermedad en una población grande pero finita. El problema de epidemias donde se toma en cuenta la cuarentena es más complicado, ya que se considera un sistema de ecuaciones diferenciales ordinarias, lo cual implica aplicar teoría de álgebra lineal.
Asimismo, otro de los equipos presentó el modelo de absorción de drogas en órganos células. En particular, explicaron que un problema importante en el campo de la medicina consiste en determinar la absorción de químicos (tales como drogas) por células u órganos.
Si se supone que un líquido transporta una droga dentro de un órgano de volumen V cm3 a una tasa de a cm3/seg y sale a una tasa de b cm3/seg. La concentración de la droga en el líquido que entra es c cm3/seg. La ecuación diferencial que modela tal problema es:
(3) (fo. 18)
cuya solución es: (4) (fo. 19)
donde se presentan los siguientes casos:
Caso 1: a = b. En este caso, la tasa a la cual entra la droga es igual a la tasa a la cual sale, y (4) se convierte en: (fo. 20)
Caso 2: a = b y x0 = 0. En este caso, las tasas de entrada y de salida son iguales, y la concentración inicial de la droga en el órgano es 0; entonces (4) resulta: (fo. 21)
Por último se valoraron otros modelos que se usan en el estudio de enfermedades dinámicas como la leucemia y otras enfermedades que afectan a las células sanguíneas. Uno de estos modelos de producción de células sanguíneas fue desarrollado por A. Lasota en 1977 e involucra la función exponencial:
p (x) = Axs e−sx/r , (fo. 22) donde A, s y r son constantes positivas y x es el número de granulocitos (un tipo de glóbulos blancos) presentes.
También se utilizan en el flujo de sangre en los vasos sanguíneos, es más rápido cuando se dirige hacia el centro del vaso y más lento hacia el exterior. La velocidad del fluido sanguíneo V está dada por:
V = p (R2 − r2)/4Lk, (fo. 23) donde R es el radio del vaso sanguíneo, r es la distancia que recorre la sangre desde el centro del vaso, y p, L y k son constantes físicas relacionadas con la presión.
Y cuando se administra una droga o vitamina intramuscularmente, la concentración en la sangre (medida en ug/ml) t horas después de la inyección se puede aproximar por medio de la función:
F(t) = C(e−k1t − e−k2t), (fo. 24) donde C , k1 y k 2 son constantes positivas.
Al concluir la discusión de los diferentes ejemplos se reflexionó colectivamente y se llegó a un consenso en el grupo sobre la importancia de la Matemática en las Ciencias Básicas Biomédicas, opinión que difiere de la emitida por la mayoría del grupo al inicio del curso escolar.
Como se explicó, la propuesta didáctica se sometió a la valoración por un grupo de 11 especialistas y se utilizó el método prospectivo Conexo en dictámenes de peritos, especialistas o expertos. 7
La encuesta aplicada y los resultados de la valoración realizada por los 11 especialistas de los aspectos consultados y los valores de la mediana de cada aspecto para datos agrupados, con los que se logra mayor precisión y discriminación del análisis, aparecen en las tablas y figuras que se muestran a continuación. (Cuadro 1)
Las evaluaciones, en un escalamiento ordinal creciente del 1 al 5, otorgadas por los especialistas a los 10 aspectos consultados se registraron en la tabla. En la última fila aparecen sintetizados los resultados a partir del cálculo de la mediana para datos agrupados, por ser la medida de tendencia central que caracteriza al escalamiento ordinal utilizado.
(fo. 25)
Donde:
![]() (simb 1): es la mediana de los registros dados por los peritos en cada aspecto consultado.
(simb 1): es la mediana de los registros dados por los peritos en cada aspecto consultado.
![]() (simb 2): es el límite inferior de la clase donde se encuentra la mediana.
(simb 2): es el límite inferior de la clase donde se encuentra la mediana.
: es el número de peritos.
![]() (simb 3): es la frecuencia acumulada en las clases anteriores a la clase donde se encuentra la mediana.
(simb 3): es la frecuencia acumulada en las clases anteriores a la clase donde se encuentra la mediana.
![]() (simb 4): es la frecuencia de la clase donde se encuentra la mediana.
(simb 4): es la frecuencia de la clase donde se encuentra la mediana.
![]() (simb 5): es el tamaño del intervalo de clase donde se encuentra la mediana, que por razones prácticas se ha elegido la unidad.
(simb 5): es el tamaño del intervalo de clase donde se encuentra la mediana, que por razones prácticas se ha elegido la unidad.
La objetividad del método comenzó desde la selección adecuada de los 11 especialistas, de los que se espera, por su alto grado de experticia en la materia, la realización de un estudio en profundidad que aseguren la emisión de criterios y juicios acertados sobre los aspectos que se ponen a su consideración. Sin embargo, ello en sí mismo no garantiza que se cumplan absolutamente dichas expectativas y una vez consultados, el método científico exige la aplicación de un procedimiento lógico para valorar el grado de fiabilidad con que han emitido sus opiniones.
Para determinar el grado de conexo entre las opiniones de los especialistas, se aplica el coeficiente de correlación multidimensional cuya fórmula tipificada es:
(fo. 26)
Donde:
![]() (simb 6) Cantidad de peritos.
(simb 6) Cantidad de peritos.
![]() (simb 7) Número de ítems.
(simb 7) Número de ítems.
![]() (simb 8) Distancia entre los rangos dados por los peritos a cada par de ítems.
(simb 8) Distancia entre los rangos dados por los peritos a cada par de ítems.
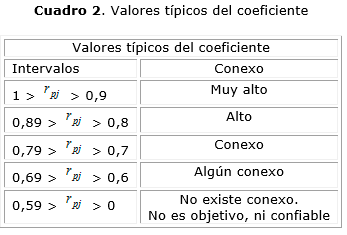
El coeficiente de correlación multidimensional , toma valores entre 0 y 1, en la medida que se acerque a 1, habrá mayor concordancia entre los criterios emitidos por especialistas. Para mayor precisión, puede utilizarse con un buen grado de aproximación, los rangos que se presentan en la tabla 3.
(Cuadro 2)
Al aplicar el coeficiente de correlación multidimensional al conjunto de datos registrados, se obtiene el valor:
(fo. 27)
Valor para el coeficiente que tipifica que se encuentra en los rangos en que existe conexo, lo cual significa que el análisis realizado por los especialistas fue objetivo y en esa medida confiable. En la figura se representan los resultados de las medianas para cada estudio agrupado por indicador.
(Fig.)
CONCLUSIONES
La propuesta didáctica, basada en la estructuración sistémica de los contenidos a partir de la resolución de clases de problemas variando los instrumentos, constituye una alternativa viable del perfeccionamiento del PEA de la Matemática, para residentes de Ciencias Básicas Biomédicas. Su puesta en práctica desde el curso 2012–2013 reveló un cambio en el modo de dirigir el PEA de la Matemática, y ha contribuido a la elevación de la motivación y la aplicación integrada de los conocimientos, métodos, modos de actuación y la posibilidad de que los residentes revelaran relaciones interdisciplinarias. Los resultados obtenidos en la consulta a especialistas sobre la pertinencia de la propuesta didáctica reveló la existencia de concordancia en los criterios emitidos por estos, en cuanto a los fundamentos teóricos, elementos que la conforman y su contribución a la dirección del PEA y al aprendizaje de los residentes, indican que estos realizaron un análisis racional de la propuesta didáctica, lo que garantiza la objetividad del resultado.
REFERENCIAS BIBLIOGRÁFICAS
1. Rodríguez T. Enfoque sistémico en la dirección de la asimilación de los conceptos básicos de la disciplina Matemática Superior [tesis]. La Habana: Instituto Técnico Militar José Martí (ITM); 1991.
2. Hernández H. Vigotsky y la estructuración del conocimiento matemático. Experiencia cubana. Conferencia Magistral RELME 11. México; 1997.
3. Delgado R. La enseñanza de la resolución de problemas matemáticos: Dos elementos fundamentales para lograr su eficiencia: la estructuración de contenido de enseñanza y el desarrollo de habilidades generales matemáticas [tesis]. La Habana: Universidad de Ciencias Técnicas José Antonio Echevarría (CUJAE); 1999.
4. Llivina M. Una propuesta metodológica para contribuir al desarrollo de la capacidad para resolver problemas matemáticos [tesis]. La Habana: Universidad de Ciencias Pedagógicas Enrique José Varona; 1999.
5. Jiménez H. Propuesta didáctico metodológica para mejorar, en los estudiantes, la disposición de los conocimientos del Análisis Matemático tanto para su referencia como aplicación [tesis]. La Habana: Universidad de Ciencias Pedagógicas Enrique José Varona; 2000.
6. González MA. Propuesta didáctica para perfeccionar el proceso de enseñanza aprendizaje de los problemas geométricos [tesis]. La Habana: Universidad de Ciencias Pedagógicas Enrique José Varona; 2002.
7. Pérez OA. Un coeficiente de correlación multidimensional para las investigaciones educativas. IV Congreso Internacional Didáctica de las Ciencias. La Habana: Sello Editor Educación Cubana; 2010.
8. González MA, Mendoza R, García L, Mendoza R, Travieso Y, Puldón G, et al. Propuesta de actividades con un enfoque interdisciplinario que favorezca la integración de las disciplinas de Ciencias Básicas [en prensa]; 2014.
9. Rosa Díaz J, Navarrte Zuazo V, Fernández Sánchez E. Variante de cálculo de infusión de midazolam en la TIVA manual. Rev Cubana de Anestesiol Reanim. 2013;12(3):198-209.
Recibido: 8 de abril de 2015.
Aprobado: 12 de julio de 2015.
Miguel Angel González Rangel . Instituto de Ciencias Básicas y Preclínicas Victoria de Girón. Calle 146 no. 3102. Playa. La Habana, Cuba. Correo electrónico: magrvirgo@yahoo.es