La búsqueda temática digital de este número de la revista se publica en momentos en que la humanidad está enfrentando un nuevo Coronavirus, SARS-Cov2, que ha ocasionado la pandemia denominada COVID-19. Este nuevo evento pone en tensión al sistema de salud de los países, así como a las escuelas y universidades de las ciencias médicas. En el manejo de la epidemia, el conocimiento para evaluar el comportamiento y realizar pronósticos que permitan la toma de decisiones en el seguimiento y control de la enfermedad, además de ajustes en los sistemas y servicios de salud que se requieran para la atención a susceptibles, sintomáticos y enfermos, adquiere suma importancia en la gestión administrativa y epidemiológica.
La epidemiología se considera una disciplina científica que estudia ladistribución, la frecuencia, las determinantes, las relaciones, las predicciones y el control de los factores relacionados con la salud y la enfermedad en poblaciones humanas. Ella tiene un lugar relevante en las ciencias biomédicas, las ciencias sociales y las ciencias exactas.1,2
En general, los problemas de salud pública han sido abordados por la epidemiología, y para ello se han utilizado modelos teóricos y metodológicos, a partir de la aplicación de diferentes métodos para la descripción y el estudio del fenómeno:1,2
Epidemiología descriptiva, que estudia el fenómeno en tiempo, lugar y personas, a través de la frecuencia y distribución de la incidencia, la prevalencia y la mortalidad.
Epidemiología analítica, basada en la observación o experimentación, a través de las relaciones causales entre “factores de riesgo” a los que se exponen las personas, las poblaciones y las enfermedades, de acuerdo con la probabilidad de riesgo absoluto (probabilidad de ocurrencia de una enfermedad en un período de tiempo dado) o riesgo relativo (probabilidad relativa de ocurrencia de dos o más riesgos).
Epidemiología experimental, basada en estudios aleatorios de distribución de los individuos en dos grupos: uno experimental y otro de control.
Ecoepidemiología, que utiliza herramientas ecológicas, para la evaluación integral de la interacción de las personas y las poblaciones con factores ambientales que puedan influir en la evolución de la enfermedad en estudio.
En el grupo de modelos teóricos y metodológicos que apoyan los estudios epidemiológicos se encuentra la modelación matemática, que establece un modelo conformado por un conjunto de símbolos y relaciones matemáticas formales que representan una aproximación a las relaciones reales existentes en el objeto de estudio.2,3
Este tipo de modelación analiza los problemas biológicos para tratar de captar sus cualidades básicas y estudiarlas, basadas lo siguiente:3
La comprensión y apreciación del fenómeno que se va a modelar.
La representación matemática de los componentes esenciales del fenómeno.
El hallazgo de soluciones útiles, expresadas de manera cuantitativa.
La interpretación biológica de los resultados matemáticos en términos visibles y predicciones.
La comparación con resultados experimentales o la observación práctica.
Los modelos matemáticos pueden clasificarse en varios grupos, entre otros están:4
Empíricos o teóricos: los primeros se basan en relaciones estadísticamente significativas entre variables que son válidas en el contexto de estudio; mientras que los segundos, en las leyes físicas y biológicas que rigen los procesos en investigación.
Deterministas o estocásticos: los primeros, entre los que se encuentran los modelos compartimentales, son aquellos que trabajan con condiciones y datos conocidos, y se pueden controlar los factores que intervienen en el estudio, por lo que no se contempla la existencia de incertidumbre o el azar; y el segundo se asocia a la probabilidad de ocurrencia, a la existe de incertidumbre en su comportamiento y no se conoce el resultado esperado.
Estáticos o dinámicos: se refieren a la forma en que se trata el tiempo. Los modelos estáticos dan un resultado agregado para todo el período de tiempo considerado. Los modelos dinámicos devuelven las series temporales de las variables consideradas a lo largo del período de estudio.
En el momento de la búsqueda fueron encontrados, mediante búsqueda simple en Google y Google Académico, los términos “modelos epidemiológicos” (10 800 000 resultados), “modelos matemáticos” (más de 759 000 resultados).
Para compartir la sección de este número de la revista, se invitó a Raúl Guinovart Díaz, decano de la Facultad de Matemáticas y Computación de La Habana; a Waldemar Baldoquín, especialista en bioestadísticas del Instituto de Medicina Tropical; a Wilfredo Morales Lezca, profesor auxiliar de la Facultad de Matemática de la Universidad de La Habana; y a Cristina Valdivia Onega, epidemióloga de II grado y directiva del sistema de salud cubano, con vasta experiencia y muy vinculados a esta temática, quienes aportarán sus criterios sobre la actualidad y el alcance de este tema en la docencia médica.
De la literatura consultada se seleccionaron aquellas que aportaban aspectos fundamentales y brindaban una visión holística del asunto. A continuación se describen:
“Modelos epidemiológicos de enfermedades virales infecciosas”. Tesis de Emilene Carmelita Pliego Pliego para la licenciatura de Matemáticas, en la Facultad de Ciencias Físico-Matemáticas de la Universidad de Puebla, México, quien, tras una breve introducción e historia de las epidemias, enuncia los conceptos básicos y los tipos de trasmisión, y aborda los modelos matemáticos y su importancia en epidemiología. También describe los antecedentes, las hipótesis, las ecuaciones diferenciales ordinarias y el análisis cualitativo de los modelos epidemiológicos de Lotka-Volterra, el modelo clásico epidemiológico susceptible-infeccioso-recuperado de Kermack y McKendric (SIR) y el modelo suceptible-infeccioso-recuperado-suceptible (SIRS). También aborda las tres cantidades umbrales R0, δ y R para modelos endémicos y de influenza. Puede descargarse desde la dirección https://www.fcfm.buap.mx/assets/docs/docencia/tesis/matematicas/EmileneCarmelitaPliegoPliego.pdf
“Modelos epidemiológicos basados en ecuaciones diferenciales”. Trabajo final de grado en Matemáticas de Iranzu Sanz Garayalde, publicado por la Universidad de La Rioja, que presenta tres modelos generales básicos: SIR, SI y SIS, que dividen a la población en tres grupos, las personas susceptibles (S), infectadas (I) y los que han superado la enfermedad, y los recuperados (R). También incluye cómo afecta una vacuna en el desarrollo de una epidemia en un modelo SIR y cómo se propaga una epidemia en el espacio mediante el modelo SI, que es uno de los más simples. Hace referencia, además, a otros modelos específicos: SIRS, SEIS, SEIR, MSIR y MSEIR, en los cuales la población se subdivide para su estudio en un mayor número de grupos; por ejemplo, SIRS modela un proceso de rebrote de la epidemia, los recuperados no quedan inmunizados y pasan a ser susceptibles nuevamente. El modelo SEIS incluye la clase de los expuestos (E) -individuos que poseen la enfermedad o han estado expuestos a ella-, muchos de los cuales pasan a ser infectados porque empiezan a manifestar los síntomas. Los modelos MSEIR, consideran una nueva clase de individuos, los portadores de la enfermedad con inmunidad pasiva, que tras cierto tiempo la pierden y se vuelven portadores de la enfermedad (M), pero que pueden no padecerla nunca. Un proceso importante para obtener buenas estimaciones en estos modelos es hacer una adecuada estimación de los parámetros que determinan el tránsito de un grupo a otro, y que resultan del análisis de los datos y las características particulares de la enfermedad y de la población. Puede obtenerse en la dirección https://biblioteca.unirioja.es/tfe_e/TFE002211.pdf
Modelos de la propagación de enfermedades infecciosas, obra de Fred Brauer y otros, publicada por la Universidad Autónoma de Occidente, Cali, Colombia. Los autores identifican la “epidemiología matemática” y ofrecen en 16 capítulos una introducción al modelado matemático: todos sobre estimación de parámetros y modelos estocásticos, entre otros, que constituyen una herramienta versátil para explorar diferentes tipos de problemas, con ejemplos de sus herramientas. Tiene su acceso en la dirección https://www.researchgate.net/profile/Carlos_Castillo-Chavez2/publication/269411966_Modelos_De_La_Propagacion_De_Enfermedades_Infecciosas/links/5494925f0cf2ec13375819b9/Modelos-De-La-Propagacion-De-Enfermedades-Infecciosas.pdf
“Modelos matemáticos en epidemiología: enfoques y alcances”, publicado por Jorge X. Velasco Hernández en el número 44 de Miscelánea Matemática en 2007, en el que el autor realiza una descripción y crítica al enfoque de modelación matemática en la epidemiología que hace uso de modelos dinámicos, particularmente ecuaciones diferenciales, aunque también trata modelos discretos y estocásticos de manera breve. Se puede acceder desde la dirección http://www.matcuer.unam.mx/~max/Misc44/Velazco_j.pdf
“Modelos matemáticos para enfermedades infecciosas”, artículo de revisión publicado en la revista Salud pública de México, vol. 49, no. 3, de 2007, por Osval A. Montesinos López y Carlos M. Hernández Suárez, de la Universidad de Colima, México, en el cual se describen la importancia y la clasificación de los modelos matemáticos en la comprensión de la dinámica de transmisión de las enfermedades infecciosas, así como en el diseño de medidas eficaces de control y erradicación de dichas enfermedades. Puede ubicarse en la dirección https://www.scielosp.org/pdf/spm/2007.v49n3/218-226/es
“Modelos de transmisión, pronóstico y gravedad del dengue”, capítulo 3 del libro Dengue, a cargo de Lizet Sánchez Valdés, Carlos R. Sebrango Rodríguez, Beatriz Vega Riberón y Lazara Alfonso Barrio, publicado por la Editorial de Ciencias Médicas de Cuba. El capítulo introduce y describe la modelación matemática del dengue en el país; los diferentes tipos de modelos utilizados; el tránsito del modelo epidemiológico al modelo matemático (SIR), y de este al estocástico; los parámetros de importancia epidemiológica; la fuerza de infección; el número reproductivo básico y el número reproductivo efectivo; el acmé epidémico o punto de retorno; el tamaño final de la epidemia, la proporción final de población infectada o el riesgo acumulado; y el umbral entomológico de transmisión y la fracción crítica de vacunación, los cuales definieron la aplicación práctica de los modelos en la vigilancia y el control del dengue; así como los retos y proyecciones de la modelación en esta enfermedad. Muchas de estas ideas pueden ser generalizadas a otros tipos de epidemias. Se puede encontrar en la dirección http://www.bvscuba.sld.cu/libro/dengue/
“Modelos epidemiológicos en redes: una presentación introductoria”, publicado en el Boletín de Matemática, vol. 22, no. 1, de 2015, por Carlos E. Álvarez Cabrera, Edgar J. Andrade Lotero y Valérie Gauthier Umaña, presenta los conceptos básicos de algunos modelos epidemiológicos en redes que, al tomar en cuenta los patrones de contacto entre individuos, contrasta con el modelo SIR, en el cual la transmisión solo depende de la densidad de individuos en cada uno de los estadios de la enfermedad. Se plantea que el modelo SIR sobrestima el máximo de prevalencia con respecto al modelo de red completa. Se presenta también el estudio mediante simulaciones en el efecto de onda que tienen las reconexiones en el modelo de mundo pequeño y se mencionan varias aplicaciones de los modelos de redes en epidemiología. Puede descargarse en la dirección https://revistas.unal.edu.co/index.php/bolma/article/viewFile/51844/51641
“Modelado de enfermedades contagiosas mediante una clase de redes sociales dinámicas”, publicado en la Revista de la Facultad de Ingeniería de la Universidad Central de Venezuela, por José Luis Herrera y Gilberto González Parra. Estudia el modelo clásico epidemiológico (SIR), mediante las redes dinámicas sociales, las cuales están basadas en grafos dinámicos, donde los nodos representan a los individuos y las conexiones entre nodos a las interrelaciones sociales capaces de transmitir enfermedades. Se realizan simulaciones del modelo estocástico a través del método de Monte Carlo y se muestra cómo la dinámica de la red afecta la evolución de las epidemias. También se aprecia cómo el grado de conectividad social y la estructura inicial de la red influyen sobre la propagación de las enfermedades infecciosas. Puede accederse desde la dirección http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S0798-40652012000200003
“Modelo SIR para epidemias: Persistencia en el tiempo y nuevos retos en la era de la informática y las pandemias”. Publicado en la Revista Cubana de Informática Médica, realiza una breve descripción del modelo, así como la interpretación de las epidemias a partir de este, con ejemplos reales, estimación de parámetros y sus aplicaciones prácticas. Concluye que este modelo es capaz de reproducir datos de disímiles epidemias y, mediante las adaptaciones correspondientes, puede extenderse a diversos tipos de enfermedades, a partir de la estimación de los parámetros, lo que permite predecir el curso de epidemia según los datos iniciales. Puede descargarse desde la dirección http://www.rcim.sld.cu/revista_13/articulos_htm/modelosir.htm
“Estimating incubation period distributions with coarse data”, publicación online de 2009, en Statitics in Medicicine, por Nicolas G. Reich, J. Lesser, A. Derek, T. Cummings y R. Brookmeyer. En su resumen plantea que el período de incubación, correspondiente al tiempo entre la infección y el inicio de los síntomas, es una medida importante en la vigilancia y control de las enfermedades infecciosas, pero con frecuencia su medición resulta inexacta. Esto ocurre porque, por lo general, no se conocen con precisión el momento de la infección -cuando se adquiere la enfermedad- y el inicio de los síntomas. Estos autores proponen dos métodos para estimar la distribución del período de incubación, que resultan útiles para la investigación en tiempo real de los brotes y epidemias, y para modelar las intervenciones. El primer método representa los datos como censurados por intervalo doble y el segundo utiliza una técnica de reducción para facilitar el cómputo de las estadísticas. Como resultado de este estudio se recomienda el uso del método de análisis de datos con censura por intervalo doble por ser más robusto. Puede accederse desde la dirección https://reichlab.io/pdfs/publications/reich-estimate-incubation.pdf
“Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures”, publicado por American Journal of Epidemiology, en el sitio Oxford Academic por Jacco Wallinga y Peter Teunis. Se proponen varios métodos para estimar R, a partir de datos de los reportes de la vigilancia epidemiológica. Los modelos mecanísticos son difíciles de generalizar debido a las presunciones subyacentes: tamaño de la población, presencia o no de un período de latencia, entre otros. Los autores presentan un método estadístico más sencillo para estimar R en el transcurso de una epidemia. Este constituye un método genérico que solo requiere los datos de la incidencia de casos y la distribución del intervalo en serie -tiempo entre el inicio de los síntomas en el caso primario y el inicio de los síntomas en el secundario-. Se basa en la reconstrucción de las probabilidades de los árboles de trasmisión y el conteo del número de casos secundarios por individuo infectado. Este método estima un valor de R por cada momento en el tiempo de la incidencia. No obstante, algunos autores describen algunas pequeñas deficiencias del método cuando el intervalo de tiempo resulta pequeño, entre otras dificultades. Se puede consultar en la dirección https://academic.oup.com/aje/article/160/6/509/79472
“A new framework and software to estimate time-varying reproduction numbers during epidemics”, publicado por American Journal of Epidemiology, en el sitio Oxford Academic, por Anne Cori, Neil M. Ferguson, Christophe Fraser y Simon Cauchemez. Los autores describen un nuevo método para estimar el número reproductivo en tiempo real, que supera las dificultades de las técnicas anteriores. Se trata de un método genérico para estimar el número reproductivo instantáneo a partir de las series de casos (incidencia). Se considera que el método es capaz de detectar los cambios en R cuando se implementan medidas de control. Además, estos crearon un libro en Microsoft Excel y una librería en R para facilitar la implementación de dichas técnicas en la práctica epidemiológica. Puede obtenerse en la dirección https://academic.oup.com/aje/article/178/9/1505/89262
También pueden consultarse algunos sitios o blogs en internet sobre este tema, que permiten profundizar en diversos aspectos que pueden resultar útiles:
PREZI. Aplicaciones que permite a los usuarios crear una presentación no lineal, donde pueden usar zoom en un mapa visual (Fig. 1).
InCyTDe. Espacio del Instituto de Ciencia y Tecnología para el desarrollo de la Universidad Rafael Landívar de Guatemala (Fig. 2).
ambientum.com. Portal profesional del medio ambiente (Fig. 3).
 Fuente:https://www.ambientum.com/ambientum/ciencia/los-modelos-matematicos-de-la-covid-19.asp
Fuente:https://www.ambientum.com/ambientum/ciencia/los-modelos-matematicos-de-la-covid-19.asp
Fig. 3 ambientum.com.
CubaData. Datos en tiempo real de la evolución de la epidemia de COVID-19 en Cuba. También ofrece una aplicación móvil para sistema Android (Fig. 4).
CubaDebate-acn. Espacio de información especial acerca de la COVID-19 en Cuba (Fig. 5).
 Fuente:http://www.cubadebate.cu/especiales/2020/04/27/covid-19-en-cuba-el-pico-se-adelanta-que-dicen-los-modelos-matematicos-y-como-interpretarlos/#.XqyxHM3B-60 y http://www.acn.cu/salud/63840-confirman-modelos-matematicos-efectividad-de-medidas-ante-la-covid-19-en-cuba
Fuente:http://www.cubadebate.cu/especiales/2020/04/27/covid-19-en-cuba-el-pico-se-adelanta-que-dicen-los-modelos-matematicos-y-como-interpretarlos/#.XqyxHM3B-60 y http://www.acn.cu/salud/63840-confirman-modelos-matematicos-efectividad-de-medidas-ante-la-covid-19-en-cuba
Fig. 5- CubaDebate-acn
Como se puede apreciar, este tema es de vital importancia para el conocimiento y abordaje de situaciones especiales como las que hoy confronta el mundo. Los modelos matemáticos brindan a la epidemiología una herramienta eficaz que permite disponer de comportamientos y proyecciones para el análisis, y tomar decisiones en el seguimiento y control de epidemias. Resulta oportuno, entonces, que los especialistas invitados lo posicionen en el entorno de la formación en las ciencias médicas de Cuba y emitan sus reflexiones al respecto.
Reflexiones sobre el tema
Cuba, desde su primera ley, la Constitución de la República,5 sienta las bases para garantizar la salud de todos sus ciudadanos. La salud pública cubana se caracteriza por mantener un sistema de salud único, gratuito y universal, con tres niveles de atención y una alta vinculación con la población y los diferentes sectores de la sociedad. Es por ello que cualquier evento epidemiológico pone en tensión todas las fuerzas para controlarlo, desde el Gobierno del país hasta el último ciudadano. De ahí la importancia de los modelos de predicción y comportamiento de epidemias y eventos adversos, que permiten al Estado tomar decisiones con un fundamento científico.
Del grupo de modelos que pudieran aplicarse en situaciones de epidemia, Cuba ha utilizado en la COVID-19, entre otros que serán objeto de estudio en otras búsquedas temáticas, el modelo SIR y el número reproductivo R.
Modelos compartimentales
Son modelos estadísticos, dinámicos y otros; que agrupa la población en compartimentos, por ejemplo, los modelos SIR agrupan a la población en compartimentos de Susceptibles, Infectados y Recuperados. El paso de un compartimento a otro se realiza a partir de una tasa de cambio que depende de las características particulares de la epidemia. Estas tasas son estimadas experimentalmente o con técnicas matemáticas: métodos de regresión, métodos de mínimos cuadrados, descenso de gradiente, entre otros.
La validación de los resultados alcanzados se comprueba con los resultados experimentales y se utiliza para dar pronóstico del comportamiento de la enfermedad.
La modelación matemática, si bien permite predecir el desarrollo completo de la epidemia, no puede reproducir con exactitud la realidad captada, pero sí da una estimación que facilita dirigir las políticas en pos de amortizar las pérdidas de vidas humanas, así como la organización de los recursos si se toman las medidas para que no se desborde el sistema de atención de salud. Estos modelos compartimentales tienen una gran variedad y pueden estudiar la acción de los medicamentos, las medidas terapéuticas, las acciones de control y administrativas para orientar sobre aquellos temas más urgentes en pos de controlar la infección.
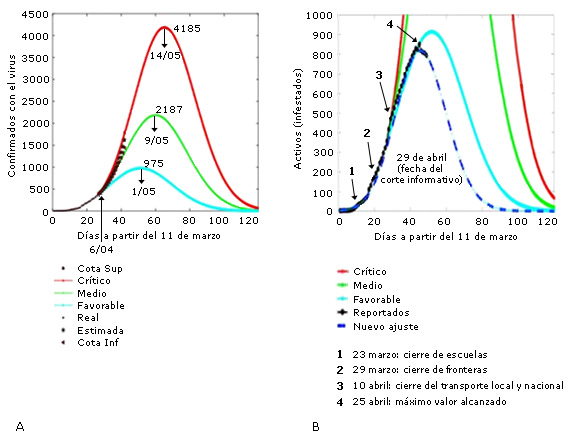
Por ejemplo, en el caso de la modelación de la COVID-19 en Cuba se presentaron a la población tres escenarios probables (Fig. 6a), de los cuales se derivaron determinadas conclusiones:
Existen posibilidades de que la pandemia sea muy severa en el país, lo cual colapsaría el sistema de salud por la cantidad de camas y equipamiento que se necesitaría.
La única forma de evitar el contagio y avanzar hacia un escenario más favorable, depende de las acciones del Gobierno, pero, sobre todo, de la capacidad de la población de cumplir las medidas de aislamiento social.
El Gobierno debe apresurar medidas previstas con el fin de reducir la movilidad de las personas y así reducir el contagio.
En la figura se observa también que, de cumplirse este pronóstico, el pico hospitalario se alcanzaría en la primera quincena de mayo y que el período de duración de la enfermedad se podría extender hasta por cuatro meses.
Estas conclusiones no fueron para nada exageradas. La experiencia internacional demostraba que países más desarrollados que Cuba habían presentado graves dificultades para combatir la COVID-19 y minimizar el número de infectados y fallecidos. La toma de medidas oportunas y eficaces por parte del Estado cubano llevó el desarrollo de la epidemia al escenario más favorable, por lo que el pico quedó, incluso, por debajo de lo estimado en 100 casos (Fig. 6b). Esta intervención del estado con la participación de todo el pueblo permitió evitar el contagio de miles de personas y, por consiguiente, salvar muchas vidas.6
Número reproductivo R
En el control de las epidemias resulta esencial el número reproductivo R. El número reproductivo básico (R0) es el número promedio de casos secundarios de la enfermedad causados por un individuo infectado en el transcurso del período infeccioso o de contagio. Este parámetro proporciona una medida de la velocidad y severidad de la propagación de un patógeno en una población determinada.
R0 describe lo que ocurriría si una persona infectada entra en contacto con una comunidad totalmente susceptible y, por tanto, es un estimado que se basa en un escenario idealizado, por lo que representa el máximo potencial epidémico de un patógeno.
Por otra parte, el número reproductivo efectivo (Re) constituye una medida derivada, que tiene en cuenta la proporción de susceptibles en la población y el hecho de que mientras la epidemia (o brote) avance, la proporción de individuos susceptibles disminuya (S/N) y la trasmisión de la enfermedad se vuelve más lenta. Por lo que Re cambia en el tiempo.
En general, el objetivo de la respuesta de salud pública durante la epidemia consiste en disminuir o detener la propagación del virus mediante estrategias de mitigación que: 1. disminuya el R0 mediante el cambio de la tasa de transmisión (por ejemplo, cerrando las escuelas) o de la duración del período infeccioso (por ejemplo, mediante el uso de antivirales), o bien 2. disminuya el Re y se reduzca el número de individuos susceptibles (por ejemplo, mediante la vacunación).
En el curso del evento epidemiológico, el valor de R cambia debido a la implementación de medidas de control, entre otros factores. El seguimiento de esta estadística en el tiempo constituye una herramienta importante para evaluar la efectividad de las intervenciones y la necesidad de intensificar los esfuerzos en el control de la enfermedad. Esto es posible porque las acciones que se implementan, orientadas al control de la epidemia, reducen R por debajo del valor umbral 1 lo más próximo a 0.
Se han propuesto varios métodos para estimar R durante una epidemia. Sin embargo, por lo general, resultan métodos difíciles de implementar por las personas que no están familiarizadas con la modelación matemática.
La educación médica superior incorpora en los diferentes currículos de las carreras de ciencias médicas, el modelado de situaciones, según corresponda. Sin embargo, en casos de epidemias debe ponerse énfasis en estas herramientas científicas para el aprendizaje de modelos que permitan su pronóstico, seguimiento y control, como parte de la formación y aplicación en los diferentes escenarios docentes y de trabajo.