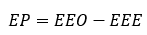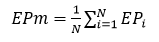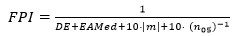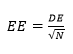Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Los avances en la tecnología de los lentes intraoculares, de los instrumentos para el diagnóstico de la catarata y del equipamiento quirúrgico, así como el perfeccionamiento de las técnicas quirúrgicas y la disponibilidad de métodos más avanzados para el cálculo de la potencia de los lentes intraoculares han hecho posible la evolución de la cirugía de la catarata, que ha pasado de ser un simple procedimiento de restauración visual a un procedimiento quirúrgico refractivo avanzado.1 A pesar de este notable progreso, lograr el rango refractivo emétrope considerado dentro de las ± 0,5 D, en más del 80 % de los casos, es un objetivo deseado, pero aún no alcanzado de la cirugía moderna de la catarata.2
Además de los parámetros biométricos fiables, la posición efectiva del lente (ELP, por sus siglas en inglés), definida como la distancia del vértice corneal al plano principal del LIO, es una variable preoperatoria no disponible, pero crucial, que debe ser predicha por todas las fórmulas de vergencia para un cálculo preciso del LIO a implantar. Se ha afirmado que la principal fuente de error en la predicción de la potencia del LIO es la estimación inexacta de la ELP.3
Para mejorar la predicción de la ELP, todas las fórmulas de vergencia incluyen en su formulación un factor de ajuste conocido como constante de lente. El valor de esta constante es, en principio, diferente para cada modelo de LIO en función de sus propiedades ópticas, dada su geometría óptica específica y la angulación de sus hápticas. Este valor es calculado por los fabricantes de lentes en base a un modelo teórico del ojo promedio de la población y a menudo es verificado y refinado sobre la base de los resultados clínicos de cierto número de cirugías con técnicas quirúrgicas estándar, antes de ser etiquetado en el paquete del LIO.1) La constante "A" utilizada por la fórmula SRK/T es la constante que suele estar impresa en la caja del LIO y puede ser convertida en cualquier otra constante utilizada por las diferentes fórmulas. Hoy en día, este proceso de conversión es realizado de forma automática por los biómetros según la fórmula seleccionada incluida en el equipo.
La constante del lente recomendado por el fabricante debe utilizarse sólo como punto de partida, ya que a menudo conduce a un cálculo inexacto de la potencia del LIO, debido a que otros factores, como los diferentes instrumentos de diagnóstico, las variaciones en la técnica quirúrgica entre los distintos cirujanos, la contracción individual de la cápsula posquirúrgica, entre otros, pueden afectar a la estimación de la ELP en pacientes concretos.1) Algunos cirujanos prefieren utilizar las constantes de lentes proporcionadas por sitios web independientes como el Grupo de Usuarios de Biometría de Interferencia Láser (ULIB; http://ocusoft.de/ulib/c1.htm) como punto de partida, en lugar de utilizar las recomendadas por el fabricante. Sin embargo, los cirujanos deberán desarrollar su propia constante personalizada para un LIO determinado con el fin de mejorar los resultados refractivos. También hay un número importante de modelos de lentes que no están incluidos en la base de datos ULIB. La optimización previa de la constante es obligatoria para cualquier estudio que investigue la precisión del cálculo de la potencia del LIO entre diferentes fórmulas. Este paso previo garantiza la eliminación de cualquier error sistemático de predicción asociado al entorno clínico como: el tipo de biómetro, la técnica quirúrgica y las características específicas de un LIO determinado.4,5
Las constantes de la mayoría de los modelos de lentes utilizados en la cirugía de catarata en Cuba no figuran en las bases de datos ULIB, por lo que la optimización de las mismas puede ser útiles como punto de partida para cualquier cirujano que utilice estos lentes específicos, antes de que puedan obtener sus constantes personalizadas. El presente trabajo se propone optimizar las constantes utilizadas por las fórmulas SRK/T, SRK/T2, Holladay 1 y Hoffer Q para cinco modelos de lentes intraoculares (LIO), implantados durante la cirugía de catarata en el Instituto Cubano de Oftalmología “Ramón Pando Ferrer” desde enero de 2006 hasta octubre de 2019, tanto para la biometría ultrasónica como para la óptica.
Métodos
Se realizó un estudio retrospectivo de 47341 ojos de pacientes (uno por paciente), operados de cataratas con implante de lente intraocular en el saco capsular sin complicaciones, desde enero de 2006 hasta octubre de 2019, en el Instituto Cubano de Oftalmología “Ramón Pando Ferrer” (ICO-RPF). Este estudio fue aprobado por el Comité Científico y Ético Institucional del Instituto Cubano de Oftalmología y el Instituto Superior de Tecnologías y Ciencias Aplicadas (InSTEC) de la Universidad de La Habana y se ajustó a los principios de la Declaración de Helsinki.
Para los pacientes con ambos ojos incluidos en la base de datos original, se hizo una elección aleatoria para seleccionar sólo uno de los ojos. Esto consistió en organizar el conjunto de datos por el número de identificación (único por paciente) y luego se seleccionó el primer ojo que aparecía en la lista. Todos los ojos debían tener registrada una refracción subjetiva a las cuatro semanas del postoperatorio.
Se excluyeron los ojos con cirugía corneal intraocular o refractiva previa, cualquier enfermedad corneal, cataratas patológicas o complicadas (traumáticas, subluxadas o postuveítis), complicaciones intraoperatorias, astigmatismo preoperatorio mayor de 3 D, agudeza visual de lejos corregida posoperatoria peor que 20/40 (0,5), queratometrías medias menores de 36,0 D o mayores de 50.9 D, sorpresas refractivas mayores de 3,0 D y falta de información refractiva postoperatoria.
Se registraron los parámetros biométricos oculares preoperatorios, incluida la longitud axial (LA), la profundidad de la cámara anterior (ACD, medida desde el epitelio corneal hasta el cristalino), la potencia corneal media (Km), y la refracción (esfera, cilindro, eje y equivalente esférico EE) antes y después de la cirugía, así como la potencia del LIO. Una parte de las mediciones biométricas se realizó con un biómetro ultrasónico (Cinescan, v. 5.05 Quantel Medical, Brezet, Francia) (22372 ojos) y el resto mediante biometría óptica (OPT) (IOL Master 3.0.2, 500 o 700, versión 1.14; Carl Zeiss Meditec AG, Jena, Alemania) (24969 ojos). Cuando se utilizó el ultrasonido, las lecturas queratométricas se realizaron mediante autorefractor-queratómetro. Dado que los casos con biometría ultrasónica (US) se realizaron con la técnica de aplanación (por no disponibilidad de copa para inmersión), el proceso de optimización de ambas técnicas biométricas se realizó por separado.
Los cinco diferentes modelos de lentes implantados a los pacientes se mencionan a continuación con su correspondiente identificador numérico entre paréntesis, por el que serán denominados en lo sucesivo: UV-Lens PC156C60/2 (432), UV-Lens PCF60 (533), Ioflex (903), SAF 6125 (933) y Ocuflex (944). Estos modelos no aparecen en las bases de datos ULIB. El número de ojos analizados para cada combinación de modelo de lente-fórmula-biómetro fue diferente: 432 (US n=12 004, OPT n= 3 493); 533 (US n=4 339, OPT n= 4 867); 903 (US n=4 815, OPT n= 9 084); 933 (US n=1 214, OPT n= 1 349); 944 (OPT n= 6 176), pero en todos los casos la cantidad fue lo suficientemente grande como para garantizar la significación estadística de los resultados. El número de casos del modelo de lente 944 medido con el biómetro ultrasónico fue escaso, por lo que no se tuvo en cuenta en los cálculos.
Se calcularon las constantes optimizadas de las fórmulas SRK/T, SRK/T2, Holladay y Hoffer Q para cada modelo de lente. El proceso de optimización se realizó de la siguiente manera:
SRK/T, SRK/T2:
Con los valores de LA, Km, la potencia del LIO y el valor de A informado por el fabricante, se calculó el valor estimado del equivalente esférico posoperatorio (EEE) para cada paciente.6 En el caso de la variante T2 de la fórmula, el cálculo se realizó como se explica por sus desarrolladores.7 El error de predicción (EP) se calculó como la diferencia del equivalente esférico obtenido (EEO) un mes después de la cirugía y el EEE.
(1)
El error de predicción medio (EPm) se calculó como:
(2)
Donde N es el número de ojos incluidos en la combinación modelo-fórmula dada. Para cada combinación se obtuvo una constante global optimizada mediante la función Tools/Goal Seek de LibreOffice Calc versión 6.0.7.3 para Ubuntu 18-04, como ha sido sugerido en la literatura.4) El algoritmo Goal Seek da resultados algo diferentes cuando cambia el valor inicial de la constante, tanto para la constante a optimizar como para el EP mínimo correspondiente. Por ello, el procedimiento se comenzó siempre con el valor de la constante del fabricante. Las fórmulas utilizadas para obtener pACD y SF a partir del valor de A brindado por el fabricante son: ACD = 0,58357 * constante-A - 63,8963; SF = (constante-A * 0,5663)-65,6008.8
Además del EP, se calculó el error absoluto medio (EAM) y el error absoluto mediano (EAMed) para expresar la dependencia de los errores con la constante optimizada utilizada:
EAM = ∑|EP|/N
EAMed = Mediana |(|EP|- mediana|EP|)|
Se halló el índice de rendimiento de la fórmula, propuesto por Haigis, disponible en www.escrs.org en la sección On Demand y recomendado por los protocolos de cálculo de LIO más actualizados.(4) Se calculó según la siguiente fórmula:
(3)
Donde DE es la desviación estándar del error de predicción, EAMed es la mediana del error absoluto, m (sesgo de longitud axial) es la pendiente de la dependencia del EP con la LA, considerada lineal (nótese que la fórmula utiliza el valor absoluto de este parámetro), y (n05)-1 es el coeficiente porcentual equivalente al inverso del porcentaje de ojos con un EP de ± 0,50 D. Se utilizó el coeficiente (n05)-1 en lugar de la notación original (n10)-1, lo que modifica el número de ojos considerados, para ajustarse al rango de EP en el intervalo ± 0,5 D, que es el sugerido por los protocolos más recientes, en lugar de ± 1,0 D propuesto por Haigis.4
Además, un nuevo índice modificado (FPI') fue propuesto por la presente investigación para obtener un parámetro diferente que determine cuál de las fórmulas de cálculo del LIO es más precisa. En este nuevo índice, la DE se sustituyó por el error estándar (EE) calculado como:
(4)
Donde N es el número de pacientes incluidos en la muestra. En segundo lugar, el coeficiente porcentual original
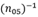fue sustituido por el modificado
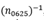, que se refiere al número de ojos con un EP dentro del intervalo de ±0.625 D. Por último, el factor de 10 seleccionado por Haigis para amplificar el valor de m en la ecuación (3) fue eliminado para este parámetro. Las razones para estas modificaciones se discuten más adelante en este trabajo.
La formulación final de este nuevo índice es:
(5)
Holladay 1:
Se utilizaron los mismos datos de entrada que en la fórmula anterior. El EEE se calculó según las fórmulas reportadas por Holladay y otros.9 La constante a optimizar fue el SF. También se calcularon los valores de FPI y FPI'.
Hoffer Q:
En este caso, se utilizaron los mismos datos de entrada y el cálculo se realizó según lo formulado por Hoffer.10,11 La constante a optimizar fue la pACD. El proceso de optimización se realizó de modo similar al utilizado para las fórmulas antes descritas.
Una vez optimizadas las constantes, se usaron para calcular los valores de la potencia del LIO que se debió implantar y el error de predicción correspondiente. Esto permitió comparar el rendimiento de diferentes fórmulas. Para determinar si los valores de las constantes calculadas para los distintos modelos muestran diferencias estadísticas, se realizó una prueba t. Para ello, las dos constantes a comparar se utilizaron para determinar el error de predicción para un conjunto de datos determinado y se compararon los valores resultantes. Los valores de p < 0,05 se consideraron significativos. Se realizó una regresión lineal simple del EP frente a la LA para encontrar m (sesgo de LA). Se comprobó la significación de todos los coeficientes. Todos los cálculos estadísticos se realizaron con LibreOffice Calc ver. 6.0.7.3 para Ubuntu 18-04.
Resultados
Las diferencias entre las constantes optimizadas y las brindadas por el fabricante fueron significativas, excepto para los valores de A y pACD del modelo 933 para la biometría US y la constante A del modelo 903, para biometría óptica. Los valores de A de las fórmulas SRK/T y SRK/T2 para un determinado modelo no mostraron diferencias significativas (tabla 1).
Tabla 1 Constantes optimizadas comparadas con los valores del fabricante para cada combinación LIO-fórmula
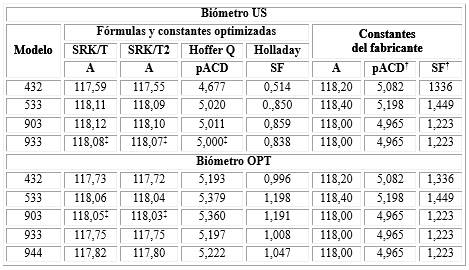
Las constantes A, SF y pACD están optimizadas para un EPm igual a cero, tanto para los biómetros ultrasónicos (US) como para los ópticos (OPT). † Calculado a partir de la A del fabricante(8 ; ‡ No diferencias significativas respecto al valor del fabricante.
La figura 1 muestra la dependencia del EP (1a), el EAM (1b) y el EAMed (1c) con la constante A optimizada de la fórmula SRK/T para el modelo 903, con el uso de la biometría óptica y la US. Se observa que la dependencia de EP con la constante A fue lineal, mientras que la del EAM fue parabólica. En cuanto al EAMed, la dependencia resultó más compleja y queda muy bien descrita por un modelo asimétrico doble sigmoidal. En todos los casos, el coeficiente de determinación ajustado (R2 ajus.) fue superior a 0,98. Obsérvese que los valores de las constantes para los que el error de predicción promedio fue igual a cero, fueron siempre diferentes de los valores de las constantes para los que se obtuvieron los mínimos de EAM y EAMed (representados por las líneas verticales en las Fig. 1a, 1b y 1c, respectivamente). Estas regularidades también se observaron para el resto de modelos y fórmulas.
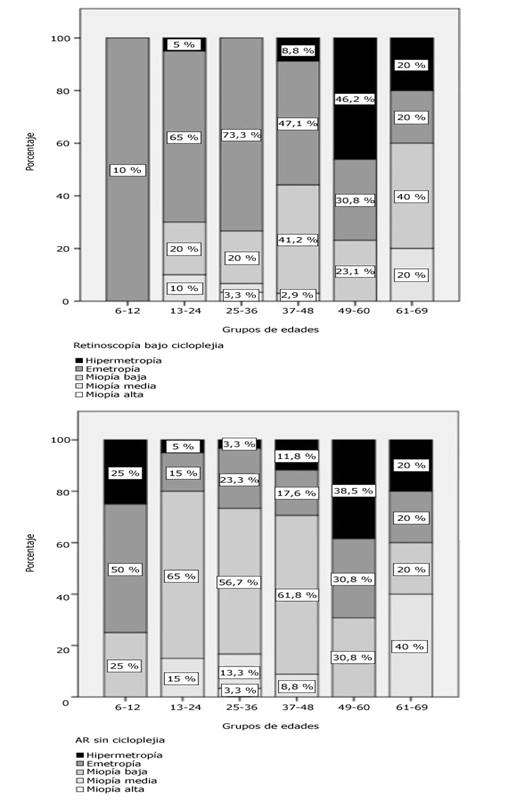
Fig 1 a) Error de predicción, b) Error absoluto medio, c) Error absoluto mediano. Dependencia de los errores con el valor de la constante A de la SRK/T para el modelo 903, tanto en biometría ultrasónica como óptica.
En la figura 2se resume el porcentaje de ojos en un intervalo dado de |EP| en función del valor de la constante A de la fórmula SRK/T, para el modelo 903. La figura 2a muestra la dependencia del porcentaje de ojos con |EP| menor o igual a 0,25 D, menor o igual a 0,50 D y menor o igual a 1,00 D en función del valor de la constante A para la biometría US. La figura 2b muestra la información correspondiente para la biometría óptica. En todos los casos las líneas son un ajuste de un modelo sigmoide asimétrico a los datos y el coeficiente R2 ajus fue mayor a 0,996 ara todas las curvas. Las líneas verticales marcan los máximos de las curvas.
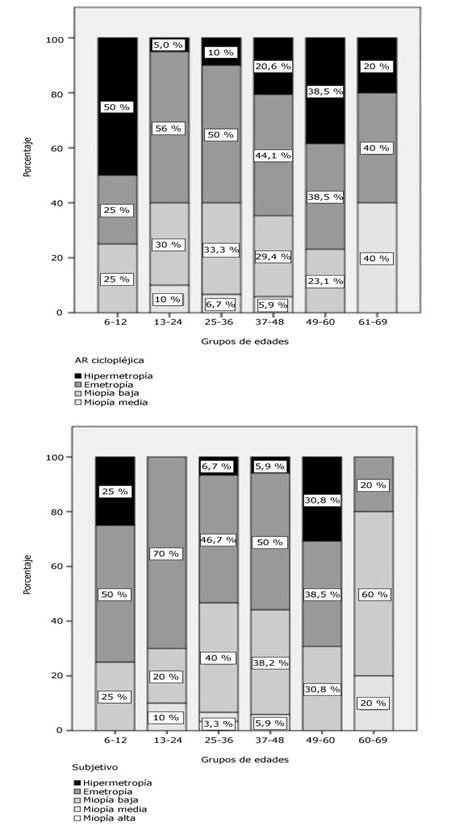
Fig 2 Porcentaje de ojos con valores absolutos de errores de predicción en los rangos ≤ 0,25 D (cuadrados), ≤ 0,50 D (círculos) y ≤ 1,00 D (triángulos) en dependencia de la constante A de la fórmula SRK/T utilizada, para el modelo 903. a) Biometría ultrasónica b) Biometría óptica.
La tabla 2 muestra la diferencia en el porcentaje y el número de ojos con un |EP| inferior o igual a 0,25 y 0,50 D entre todas las fórmulas para el modelo 903, según dos criterios de optimización diferentes. La primera columna de datos muestra el porcentaje de ojos (entre paréntesis el número de ellos) con valor absoluto de EP menor o igual a 0,25 D, cuando se utilizan las constantes mostradas en la tabla 1. La segunda columna es similar, sólo relacionada con los ojos con |EP| menor o igual a 0,50 D. Estas dos columnas muestran los valores obtenidos cuando se optimiza la constante para obtener un EPm nulo. La tercera columna brinda el valor de la constante correspondiente que produce el máximo número de ojos con |EP| menor o igual a 0,25 D (entre paréntesis su diferencia respecto al valor de la tabla 1). Las dos últimas columnas son similares a las dos primeras columnas de datos, solo que calculadas para el valor de la constante que aparece en la tercera columna de datos. Se puede observar que cuando se utilizó el valor máximo de |EP| ≤ 0,25 como criterio de optimización, el porcentaje de ojos entre ≤ 0,25 y 0,50 fue en promedio alrededor de un 2 % mayor que el obtenido cuando la optimización se consideró como EPm = 0,0 D, lo que representó un incremento no despreciable del número de ojos con menor error refractivo. Para los demás modelos los resultados fueron equivalentes.
Tabla 2 - Comparación del número y porcentaje de ojos con un determinado EP según dos criterios de optimización diferentes, para el modelo 903, tanto para la biometría ultrasónica como para la óptica
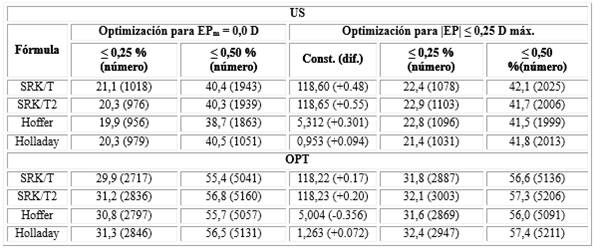
US: biometría ultrasónica. OPT: biometría óptica. EPm = 0,0 D: error de predicción promedio nulo; |EP| ≤ 0,25 D máx.: número máximo de ojos con error de predicción absoluto menor o igual a 0,25 D; Const. (dif.): valor de la constante con el que se alcanza el número máximo de ojos con un valor absoluto de EP menor o igual a 0,25 D (su diferencia respecto al valor de la constante mostrada en la tabla 3)
Además, para determinar el rendimiento de las fórmulas se calculó el FPI y el FPI' para cada combinación de fórmula-biómetro. Se observa que, con el uso de la biometría ultrasónica, la SRK/T (modelos 432 y 933) y la SRK/T2 (modelos 533 y 903) mostraron los mejores rendimientos, según ambos índices. En el caso de la biometría óptica, la SRK/T y la SRK/T2 obtuvieron también los índices más altos, excepto en los modelos 533 y 944, donde Holladay 1 obtuvo el mejor rendimiento (Tabla 3).
Tabla 3 - Índices de predicción de fórmulas para todo el conjunto de combinaciones modelo-fórmula
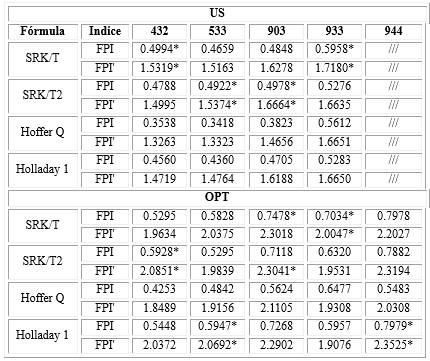
US: biometría ultrasónica. OPT: biometría óptica. FPI: Índice de rendimiento de la fórmula (índice original de Haigis); FPI': índice de rendimiento de la fórmula modificado (nuevo índice propuesto en este trabajo).* Resultados de la fórmula con el mejor índice para un modelo determinado.
Discusión
Todos los lentes intraoculares incluidos en este estudio son monofocales, biconvexos, de una sola pieza. Cuatro de ellas son plegables, de acrílico hidrofílico (hidrogel), mientras que sólo una (432) es un LIO rígido de polimetilmetacrilato (PMMA). Las características restantes que difieren entre ellas en algunos casos, tal como se muestra en la tabla 1, como el diseño de la óptica y la angulación de las hápticas, afectan la posición del lente dentro del ojo y en consecuencia al valor de la constante A proporcionada por los fabricantes para ajustar el resultado en función del tipo de LIO concreto. Aunque hay otros factores que pueden modificar el valor de la constante, como el tipo de biómetro e incluso la técnica quirúrgica, muchos de los parámetros dependientes del LIO no varían, ni siquiera entre distintos cirujanos. Por ello, las bases de datos en línea, como el sitio web ULIB, recopilan las constantes de muchas de los lentes intraoculares más utilizados, como mejor punto de partida que los valores nominales.12
Los lentes intraoculares incluidos son los disponibles en el entorno quirúrgico del autor. Aunque se comercializan en varios países de Asia, Europa y América, sus constantes A no figuran en las bases de datos ULIB. Como se expone en la tabla 2, el gran número de casos incluidos en las muestras de cada combinación modelo-fórmula para el proceso de optimización garantiza una representatividad adecuada que permite el uso de estas constantes optimizadas como un mejor punto de partida para su personalización que las constantes proporcionadas por el fabricante. Aunque el modelo 432 es un LIO no plegable que se utiliza menos en la actualidad, su constante optimizada puede ser aún de utilidad en los países en los que la extracción extracapsular del cristalino (EECC) es aún la técnica quirúrgica predominante.
Dado que las constantes optimizadas (para obtener un error medio de predicción nulo) muestran, salvo excepciones, diferencias significativas con respecto a las suministradas por el fabricante para todas las combinaciones modelo-fórmula (ver tabla 1), es obvio que el uso de los valores nominales de estos lentes no es el mejor punto de partida para obtener buenos resultados refractivos. Debido a que no se encontraron datos sobre la optimización de las constantes referidos a estos lentes intraoculares específicos, no es posible la comparación con la literatura.
Los valores muy similares de la constante A optimizada para la SRK/T y la SRK/T2 para todos los modelos, tanto con la biometría ultrasónica como con la óptica, era de esperar. Puesto que el comportamiento no fisiológico de la SRK/T que debe corregirse con la T2 se produce en muy pocos ojos con longitudes axiales superiores a 36,20 mm, la diferencia entre ellas es insignificante desde el punto de vista clínico, como se señala en el artículo original en el que se formuló la modificación de la T2.7
Cabe destacar que la dependencia del EPm, EAM y EAMed con la constante A muestra, de forma respectiva, una distribución lineal, parabólica y asimétrica doble sigmoidal, tanto para la biometría ultrasónica como para la óptica. En todos los modelos de ajuste utilizados, el valor de la constante con el que se alcanza el mínimo para cada una de estas variables difiere del proporcionado por el fabricante, para ambos métodos biométricos. Al no disponer de una copa para realizar la biometría ultrasónica por técnica de inmersión y utilizar en su lugar la técnica de contacto, los mejores resultados observados con la biometría óptica respecto a la ultrasónica son esperables, al considerar el error en la LA, inducido por el aplanamiento en este último tipo de biometría. Por ello, los resultados de ambas técnicas no se comparan sin que se analizan por separado.
La dependencia lineal del EPm y el comportamiento parabólico del EAM con la constante A concuerdan con lo obtenido por Aristodemou y otros,13 quienes describen patrones de dependencia similares para un LIO hidrofílico plegable de una sola pieza con el uso de la biometría óptica. Sin embargo, en el trabajo de estos autores, los valores de A correspondientes al mínimo del EAM y el valor cero del EPm coinciden, mientras que en el presente trabajo dichos valores, son siempre diferentes, lo cual implica una diferencia importante que tiene profundas consecuencias en la interpretación del proceso de optimización. El cambio en A implica diferentes valores del número de ojos con un EP dado. Se puede observar que el máximo porcentaje de ojos en cada rango se alcanza para un valor diferente de A. Por lo tanto, en dependencia del valor de la constante A seleccionada, se obtendrán diferentes criterios de optimización. Esta diferencia es pronunciada en la biometría US, mientras que en la biometría óptica los valores de A para los cuales se alcanza el máximo de ojos con EP ≤ 0,25 D y ≤ 0,50 D, coinciden.
La diferencia porcentual de ojos menores o iguales a 0,25 y 0,50 D, al comparar ambos criterios de optimización, confirma que existen diferencias notables en el número de ojos que alcanzan la emetropía cuando se aplican distintos criterios.
El Dr. Haigis propuso el FPI en un intento por disponer de una métrica única para demostrar la mayor precisión de una fórmula sobre otra. Cuanto más alto sea el FPI, más precisa será la fórmula.4 Hay tres aspectos relacionados con este índice que se discuten a continuación y constituyen las razones para la introducción de este nuevo índice FPI'.
El primero está relacionado con el hecho de que la DE disminuye con el incremento del número de observaciones. Esto significa que el rendimiento de una fórmula dada cambia si el número de pacientes incluidos en la muestra varía de forma notable, influyendo en el resultado de la comparación si el tamaño de las muestras a comparar es diferente entre las distintas combinaciones lente-fórmula. Esto indica que una mejor magnitud para evaluar las fórmulas sería el EE por ser menos sensible al número de datos incluidos. Además, también proporciona una medida de la exactitud de la media de la muestra respecto a la media de la población estudiada.
En segundo lugar, tal y como se indica en una carta de Fernández y otros a la revista Ophthalmology,14 la discretización del EP recomendada hasta el presente para calcular los porcentajes acumulativos, y utilizada, por ejemplo, en la Ecuación (3), podría dar lugar a un sesgo importante. Para disminuir este sesgo, dichos autores proponen utilizar una segmentación de ± 0,325 D; ±0,625 D; ±0,875 D; ±1,125 D y así sucesivamente. Según esta propuesta, el coeficiente porcentual modificado se calculó como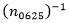 
para la presente investigación.
Por último, el factor de 10 seleccionado por Haigis para amplificar el valor de m en la ecuación (3) provoca que la fórmula sea muy sensible a la pendiente de la relación lineal entre LA y EP (sesgo de LA), en detrimento del importantísimo número de ojos pertenecientes al rango emétrope. Para corregirlo, se eliminó dicho factor, lo que aumenta la importancia del coeficiente porcentual.
Que ambos índices señalen a la SRK/T2 y SRK/T como las fórmulas con mayor grado de precisión, podría explicarse por el hecho de que la refracción subjetiva no es invariable, y puede llevar a un sesgo no aleatorio (i.e., cuando se asume el plano para 20/20), cuya aparición es más probable cuando los datos provienen de refracciones realizadas por múltiples optometristas y se analizan largos periodos de tiempo.14 Esto provoca que el menor error de predicción se obtenga con la fórmula que se utilizó para calcular la potencia del LIO implantado. Aunque la fórmula SRK/T2 no se utilizó en los cálculos originales, es importante señalar que su rendimiento es similar al de la fórmula SRK/T, que sí es utilizada con frecuencia, sola o en combinación con otras fórmulas.
De hecho, la fórmula SRK/T fue la más utilizada, según el porcentaje de ojos calculados con SRK/T (31 %); Holladay (12,5 %); Hoffer Q (5,5 %) y SRK/T + Holladay (29,6 %), por lo que no sorprende que los mejores FPI se hayan obtenido con ella.
En cuanto al nuevo índice propuesto, de nuevo la fórmula SRK/T2 obtiene el mayor grado de precisión tanto para la biometría ultrasónica como para la óptica. El FPI' da menos importancia relativa al sesgo AL. Se puede observar en los valores de FPI y FPI' para el biómetro óptico, donde FPI es mejor para SRK/T, debido al menor valor de m, pero FPI' es mejor para SRK/T2, porque los otros estadígrafos son mejores para esta fórmula. El sesgo introducido en el índice por la diferencia en el número de ojos para cada modelo se reduce al utilizar el error estándar en lugar de la desviación estándar. Para el resto de modelos, a pesar de las diferencias en la formulación de FPI y FPI', ambos índices coinciden en señalar las mismas combinaciones LIO-fórmula como las de mayor grado de precisión.
Por lo reciente de su introducción, sólo se encontró un artículo que informaba el uso del FPI para determinar la precisión de las fórmulas.15 Cabe destacar que los valores de FPI publicados en ese estudio son 10 veces inferiores a los obtenidos en el presente estudio. La forma diferente de calcular el coeficiente n entre ambos estudios es la razón de este desacuerdo. Puesto que la expresión (n10)-1 de la ecuación original es una notación un poco confusa, los autores del mencionado artículo definieron el coeficiente n como el valor decimal del porcentaje: por ejemplo, en caso de un 65 % de ojos con EP dentro de ± 0,50 D, utilizan 0,65 para el cálculo (comunicación personal, de noviembre de 2021). Al recalcular el FPI y el FPI' según el método de estos autores, los valores son bastante similares. No obstante, entre las fórmulas de tercera generación incluidas en ese estudio, la SRK/T muestra un mejor FPI que la Hoffer Q, lo que coincide con los resultados de este trabajo.
En la actualidad, es difícil asegurar cuál de las fórmulas es la más precisa, ya que se utiliza más de un criterio para ello, como el menor EAM, EAMed o el mayor porcentaje de ojos con una EP dentro de 0,25 D.4) Por ello, se justifica el planteamiento de Haigis de contar con un índice único en la determinación de cuál de las fórmulas de cálculo de lentes intraoculares alcanza la mayor precisión, como la mejor manera de estandarizar los resultados de los diferentes estudios. El futuro de este índice, de la nueva propuesta de FPI' o de otras métricas a desarrollar, depende de un mayor número de investigaciones que demuestren cuál de ellas resalta mejor las diferentes características de los resultados refractivos y su relevancia en la definición del mejor método de cálculo de LIO. También estará relacionado con la definición adecuada - y el consenso - de qué es lo óptimo en los resultados de la cirugía de catarata y cómo se refleja en una fórmula única.
Una posible limitación de este estudio es el sesgo que puede surgir al introducir datos de varios cirujanos y refracciones realizadas por diferentes optometristas, aunque se ha demostrado que el impacto de este hecho en los resultados es mínimo.13,16 Otra limitación es la no optimización de las constantes para las fórmulas más modernas, ya que la mayoría de ellas no están publicadas, lo que hace imposible optimizarlas con el método descrito en este trabajo. Por otro lado, el gran número de casos utilizados en el proceso de optimización para cada combinación LIO-fórmula proporciona una robusta significación de los resultados, lo cual es un punto fuerte de este estudio que es poco probable conseguir con los datos de un solo cirujano.
Este trabajo proporciona las constantes optimizadas utilizadas por las fórmulas SRK/T y T2, Holladay 1 y Hoffer Q para cinco modelos de LIO, no reportadas en las bases de datos ULIB, que pueden ser útiles como punto de partida para cualquier cirujano de todo el mundo que utilice habitualmente estas LIOs específicas, antes de obtener las constantes personalizadas. Se obtienen mejores resultados en la cirugía de cataratas cuando se utilizan constantes optimizadas para todas las combinaciones LIO-Fórmula. Sin embargo, los distintos criterios de optimización conducen a resultados diferentes. Así, se exponen los valores del FPI y del nuevo FPI' introducido, buscando un índice único y fiable como solución práctica para estandarizar los resultados de todas las investigaciones sobre este tema, aunque son necesarios más estudios sobre este tipo de métricas.
