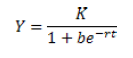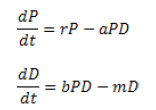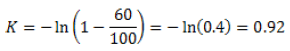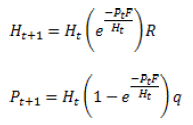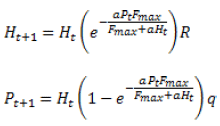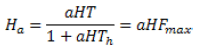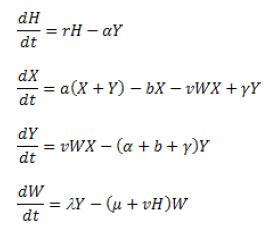Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de Protección Vegetal
versión impresa ISSN 1010-2752
Rev. Protección Veg. vol.29 no.3 La Habana sep.-dic. 2014
ARTÍCULO RESEÑA
Modelación matemática de la dinámica de poblaciones: desarrollo histórico y uso práctico en Cuba
Mathematical modeling of the population dynamics: historical development and practical use in Cuba
Ileana Miranda
Dirección de Sanidad Vegetal, Centro Nacional de Sanidad Agropecuaria (CENSA), Apartado 10, San José de las Lajas, Mayabeque, Cuba. Correo electrónico: ileanam@censa.edu.cu.
RESUMEN
La modelación matemática ha cobrado auge en los estudios ecológicos, ya que permite optimizar el uso de controles biológicos al determinar las condiciones de equilibrio del ecosistema. Se recoge la evolución histórica de la modelación matemática en el campo de la ecología cuantitativa de poblaciones y las investigaciones realizadas en Cuba. Se muestra la utilidad práctica del método grados-días como instrumento de medición. Se presentan los modelos de crecimiento y dinámica más conocidos: logístico, presa-depredador y hospedante-parásito. Por último, se mencionan las modificaciones realizadas al modelo Lotka-Volterra y la factibilidad de modelar la dinámica del ciclo de vida, incluyendo todas las fases de la población que se estudia. Se establecen, entre los retos para la temática en Cuba: a) desarrollar estudios que permitan determinar la influencia de los cambios de temperatura ambiental en los parámetros biológicos de poblaciones plagas en cultivos de importancia económica; b) implementar nuevas variantes de modelación como son la estadística bayesiana y la geo-estadística para aumentar el nivel de las predicciones; c) continuar el trabajo multidisciplinario encaminado a incorporar la interpretación biológica de los modelos matemáticos en la toma de decisiones para el manejo integrado de plagas.
Palabras clave: Biomatemática, Ecología Cuantitativa de Poblaciones, modelos poblacionales, temperaturas umbrales, Manejo Integrado de Plagas.
ABSTRACT
The mathematical modeling has the highest point in the ecological studies because it allows optimizing the use of biological controls when determining the conditions of balance in the ecosystem. The historical evolution of the mathematical models in the field of the quantitative ecology of populations and the investigations carried out in Cuba are shown. The practical utility of the grades-days method as a measuring instrument is illustrated. The most known growth models, such as the logistical, prey-predator and host parasite, are presented. Lastly, we refer to the modifications carried out to the Lotka-Volterra Model and the feasibility of modeling the dynamics of the life cycle. For this topic in Cuba, the challenges established were: a) development of studies determining the influence of the environmental temperature changes on the biological parameters of pest populations in crops of economic importance, b) implementation of new modeling variants like the bayesian statistics and geo-statistics to increase the level of the predictions, c) continuation of multidisciplinary works guided to incorporate the biological interpretation of the mathematical models in the making of decisions in the integrated pest management.
Key words: Biomathematics, Quantitative Ecology of Populations, population models, temperature thresholds, Integrated Pest Management.
INTRODUCCIÓN
La biología de sistemas es el campo de investigación interdisciplinaria de los procesos biológicos, en el que las interacciones de los elementos internos y externos, que influyen en el desarrollo del proceso, se representan con un sistema matemático. Este enfoque «holístico» o «global» permite comprender integradamente el funcionamiento de los sistemas biológicos y profundizar en el entendimiento de cómo sus interacciones internas y con otros sistemas conllevan a la aparición de nuevas propiedades. Prácticamente, cualquier proceso biológico puede ser objeto de estudio de la biología sistémica, por ejemplo, el crecimiento de una célula, la interacción entre dos bacterias o la circulación sanguínea en un organismo. La biología sistémica comenzó a desarrollarse en los años sesenta del siglo XX, pero se estableció como disciplina académica alrededor del año 2000 (1).
Dentro de este campo se encuentra el estudio de la dinámica de poblaciones como sistema biológico de interacciones. La dinámica de poblaciones fue, tradicionalmente, el campo dominante de la biología matemática. Está relacionada con otra área activa de investigación en biomatemática: la epidemiología matemática, e incluye el estudio de las enfermedades infecciosas que afectan las poblaciones. Varios modelos de dispersión viral se propusieron y analizaron, y estos proveen resultados importantes que pueden ser aplicados a estrategias de control (2).
En el campo de la Sanidad Vegetal, el uso de modelos matemáticos en la predicción de la dinámica poblacional inició con los estudios obtenidos a partir del Modelo Lotka-Volterra (3). Sin embargo, no se ha implementado una guía práctica para establecer adecuadamente estos modelos. Muy pocos modelos permiten predecir la dinámica de las poblaciones de manera efectiva (4). Se considera que la literatura, en la temática de modelación matemática en el campo de la ecología, aunque amplia, está dispersa. Por ello, el objetivo de este artículo fue realizar un análisis de tópicos relevantes del desarrollo histórico de la temática de modelación matemática aplicada a la Sanidad Vegetal.
PARTE ESPECIAL
Aunque la modelación matemática es bien empleada en los estudios de predicción, se hace necesario acotar su utilidad práctica en el campo de la Sanidad Vegetal. Desde la regresión lineal, pasando por modelos no lineales hasta llegar a los sistemas de ecuaciones diferenciales, el presente trabajo aborda la metodología a seguir, como sugerencia para trabajos futuros en la Biomatemática.
MODELANDO LA TASA DE DESARROLLO DEL INSECTO EN FUNCIÓN DE LA TEMPERATURA
Al igual que otros organismos vivos, los insectos son capaces de sobrevivir únicamente dentro de ciertos límites marcados por factores ambientales, como la temperatura, la humedad relativa o el fotoperiodo. Dentro de este rango, estos factores influyen, a su vez, sobre el nivel de respuesta de actividades, tales como: la alimentación, la dispersión, la puesta o el desarrollo (5).
De todos los factores ambientales, el que ejerce un efecto mayor sobre el desarrollo de los insectos es la temperatura. Ello es debido, principalmente, a su importante incidencia sobre los procesos bioquímicos, al ser organismos poiquilotermos. Por tanto, la influencia de la temperatura sobre el tiempo de desarrollo, como instrumento de predicción, fue ampliamente utilizada (6).
La posibilidad de desarrollo de los insectos se produce dentro de un intervalo determinado de temperaturas. Si se mide el tiempo de desarrollo, utilizando valores puntuales próximos de temperatura y se representan los resultados en ejes cartesianos, aparece una curva en forma de «J» invertida (Fig. 1a). Si lo que se representa en función de la temperatura es la tasa de desarrollo, definida como la inversa del tiempo de desarrollo y que, por tanto, mide la porción de desarrollo avanzada por unidad de tiempo, la curva resultante tiene forma sigmoidea (Fig. 1b).
En el límite térmico inferior, la curva (Fig 1b) se aproxima al punto cero de desarrollo asintóticamente, porque los insectos sobreviven frecuentemente durante largos periodos de tiempo a bajas temperaturas con un desarrollo lento. Por esta razón, la temperatura a la que ocurre el desarrollo inicial (UmD) es difícil medirla con precisión. A medida que las temperaturas se incrementan la tasa de desarrollo aumenta, y se puede ajustar la función a una recta en la zona intermedia. Conforme nos acercamos a la temperatura óptima (TO) (aquella en que la tasa de desarrollo es máxima), el desarrollo comienza a enlentecerse, hasta decaer bruscamente. Además, a temperaturas superiores a la óptima, los porcentajes de mortalidad son muy elevados, lo que hace también difícil el estudio del desarrollo a altas temperaturas y, por tanto, el establecimiento del Umbral Máximo de Desarrollo (UMD) (temperatura por encima de la cual el insecto no puede desarrollarse) (7).
Este método fue empleado con efectividad en el cálculo de temperaturas extremas para artrópodos, y permitió determinar los umbrales mínimo y máximo de desarrollo (8).
El método de grados-día como instrumento de predicción
A lo largo de los años, varios métodos se basaron en la relación tasa de desarrollo-temperatura con fines predictivos. De todos ellos, el más extendido es el llamado método de grados-día. Los grados-día (ºD) representan la acumulación de unidades de calor por encima de cierta temperatura, durante un período de un día (en el caso de los insectos, esa cierta temperatura es el umbral mínimo de desarrollo). Para cada día, se calcula la diferencia entre la temperatura media diaria y el umbral mínimo de desarrollo.
Para poder predecir el estado de desarrollo de un organismo a partir de los grados-día, es necesario haber establecido antes, además del umbral mínimo de desarrollo, la integral térmica, definida como el número de grados-día que han de ser acumulados para que ocurra un evento determinado, por ejemplo: eclosión, mudas larvarias o ninfales, pupación, emergencia del adulto. De este modo, se puede estimar cuándo va a tener lugar ese evento, acumulando grados-día hasta alcanzar el valor de su integral térmica correspondiente.
La modelización de la relación «tasa de desarrollo-temperatura» como base para el cálculo de umbrales mínimos de desarrollo e integrales térmicas
Es un hecho que el umbral mínimo de desarrollo varía entre especies de insectos y entre estados y estadios. Del mismo modo, la integral térmica es diferente para eventos distintos y, entre especies diferentes, para un mismo evento.
Para determinar de estos valores, se propusieron numerosos modelos empíricos y biofísicos que describen la relación entre la tasa de desarrollo y la temperatura. A continuación se hace una breve reseña de los principales modelos.
El primer modelo utilizado fue el Modelo Lineal, que asume la relación válida entre tasa de desarrollo y temperatura y se describe como una recta. El umbral mínimo de desarrollo se determina tomando el valor del punto de corte de la recta con el eje de abscisas. Aunque es un modelo válido para temperaturas intermedias, no se ajusta a la realidad, tanto a temperaturas bajas como altas (Fig. 1b), lo que impide un correcto cálculo de los umbrales mínimo y máximo de desarrollo, así como de la temperatura óptima y la integral térmica. No obstante, este modelo se utiliza desde hace mucho tiempo por diversos autores, dada su sencillez de cálculo y manejo y porque, en muchos casos, representa una aproximación aceptable (9, 10).
Diferentes investigadores propusieron modelos con la intención, sobre todo, de mejorar el cálculo del umbral mínimo de desarrollo. Así, en 1983, Hilbert y Logan (11) describieron el Modelo de Logan tipo III, cuya expresión matemática es combinación de dos funciones. La primera para cubrir la parte ascendente de la tasa de desarrollo y la segunda para la región descendente de la misma. Con igual objetivo fue propuesto el Modelo de Lactin (12), cuya mejora con respecto al anterior es su mayor rigurosidad, respecto a lo descrito matemáticamente por debajo del umbral mínimo de desarrollo. El modelo de Logan tipo III no es biológicamente correcto en este sentido, pues predice un aumento de la tasa de desarrollo a temperaturas inferiores a ese umbral, aspecto corregido en el Modelo de Lactin.
En la actualidad se siguen estudiando modelos cuyo objetivo principal es el de reducir el número de parámetros utilizados. Así, en 1999 se propuso un nuevo modelo que consiguió muy buenos ajustes y permitió seguir obteniendo el umbral mínimo de desarrollo (13).
La aplicación práctica de estudios de relación grados/días es importante, ya que muchas de las decisiones que son tomadas en los sistemas de manejo integrado de plagas, como son la destrucción de residuos de cultivos, elección de la fecha de siembra, liberación de enemigos naturales, entre otras, dependen del estado de las poblaciones. Será clave, por tanto, conocer dicho estado para aumentar las posibilidades de acierto en esa toma de decisiones.
Para una correcta aplicación del Método de grados/día es importante tener en consideración que todos los modelos de predicción de la tasa de desarrollo, en función de la temperatura antes mencionados, se obtienen sometiendo poblaciones de la especie en cuestión, a temperaturas constantes en laboratorio. No se consideran, por tanto, los ciclos diarios de temperatura que ocurren realmente en el campo. Por ello, se han propuesto métodos alternativos al de grados/día, para predecir el tiempo de desarrollo en condiciones de campo (14).
Sobre la base de lo anterior, siempre que un método de grados/día vaya a ser utilizado como elemento de predicción, es conveniente hacer comprobaciones del grado de fluctuación de los valores de la tasa de desarrollo a una temperatura constante y a un ciclo diario de temperaturas, cuya media coincida con la anterior. También es importante determinar los umbrales de desarrollo y los requerimientos en cuanto a integrales térmicas, utilizando poblaciones de la zona donde se va a aplicar el método. Por último, es necesario validar el modelo empleado en condiciones de campo (14).
Es posible que en algún caso, otros factores ambientales tengan un efecto sobre el desarrollo que no sea despreciable respecto al efecto de la temperatura. Puede ser el caso de la humedad relativa o el fotoperiodo (5).
En lo adelante, para emplear el método grados/días como estudio de predicción a diferentes temperatura (X1, X2,..,Xn), es aconsejable contar el tiempo de duración del insecto de huevo - adulto y elaborar una base de datos con las variables temperatura (X) y tiempo de desarrollo (Y): posteriormente, estimar la regresión lineal Y=a+bX. Consecuentemente, se debe calcular la temperatura umbral o cero biológico según la ecuación: TU=-a/b y las unidades de calor o constante térmica como: UC=Yi(Xi-TU) donde Yi es el tiempo de desarrollo alcanzado a una temperatura Xi (15).
MODELOS POBLACIONALES
Un modelo de un sistema biológico se convierte a sistemas de ecuaciones, aunque la palabra modelo es a menudo usada como el sistema de las ecuaciones correspondientes. La solución de las ecuaciones, ya sea por medios analíticos o numéricos, describe cómo el sistema biológico se comporta, en el tiempo o en equilibrio. Existen diferentes tipos de ecuaciones y el tipo de comportamiento que puede ocurrir es dependiente, tanto del modelo como de las ecuaciones utilizadas. El modelo, a menudo, hace suposiciones sobre el sistema. Las ecuaciones pueden también hacer suposiciones sobre la naturaleza de lo que puede ocurrir (1).
Los modelos clásicos en ecología son presa-depredador, competencia interespecífica (Lotka/Volterra) y el crecimiento logístico de las poblaciones de seres vivos en un medio con recursos limitados (Verhulst) (2). Otros modelos fueron desarrollados en correspondencia con la interpretación de las relaciones en el ecosistema.
Crecimiento Logístico
El modelo logístico fue desarrollado por el matemático Peirre Verhulst en 1938, y sugiere que la población no crece ilimitadamente, sino que sigue un crecimiento hasta alcanzar una capacidad máxima K simulando una curva logística según variaciones de tiempo t (2):
El parámetro r en el modelo se interpreta como la tasa de incremento poblacional en ausencia de competencia intraespecífica. Si la población inicial es menor que K, la curva es logística; si es mayor que K, la población decrece, y si coincide con el valor de K, la población no cambia.
Los parámetros K, b y r se determinan a través de una regresión no lineal, donde la variable independiente es el tiempo (intervalo de muestreo si, por ejemplo, es quincenal t=0,15, 30,…) y la variable dependiente es la densidad poblacional.
El parámetro r se compara con la tasa intrínseca de incremento rm, determinada a través de las tablas de vida (16). Otros parámetros de interés biológico también son calculados experimentalmente (Tabla 1).
Además de calcular estos parámetros, se suele graficar la curva de supervivencia lx, pues esta resulta también un modelo matemático. Dicha curva se emplea para el estudio de la biología tanto de una presa (17) como de un depredador (18). Para los áfidos (19) y los parasitoides, por ejemplo, se sigue un estudio similar, donde resultaran importantes los parámetros tasa intrínseca de incremento (rm), tasa neta de reproducción (Ro), el tiempo promedio que transcurre entre dos generaciones (T) y el tiempo de duplicación de la población (TD) (20).
Para facilitar estos cálculos se implementó el software TaviSoft (21).
Modelo Presa-Depredador
La dinámica natural de una población no puede ser predicha sin conocer la dinámica de interacción con su enemigo natural (2). Las dinámicas de interacción más estudiadas son las de antagonismo ecológico, donde una especie toma ventaja de la otra. En este sentido, el modelo más estudiado es el presa depredador (3). Este modelo tiene como inconveniente que la pérdida en densidad de la presa es solo atribuida a la acción del depredador. Sin embargo, el estudio del punto de equilibrio nos dota de información sobre el nivel de densidad del depredador que logra una disminución en la densidad de la presa (22).
El modelo se representa por el sistema de ecuaciones:
Donde:
r : tasa intrínseca de incremento de la presa. Esta se estima colocando una determinada cantidad de individuos en ausencia del depredador y realizando el conteo diario hasta que todos los individuos mueren. La cantidad inicial de individuos está en dependencia de la presa que se estudia (19).
a: Coeficiente de depredación. Se coloca un depredador con determinado nivel de presa y se estima, al cabo de n días, el número de individuos muertos. Se calcula el factor K:
Entonces a=K/n
Por ejemplo, si de un total de 100 áfidos, 60 son depredados al cabo de dos días, entonces:
Y por tanto, a=0.92/2=0.46
b: es la tasa de reproducción del depredador por una presa ingerida.
m: es la tasa de mortalidad del depredador. Experimentalmente, se colocan diferentes niveles de presa (P) y se determina la tasa de incremento del depredador (rd). Esto permitirá estimar b y m, parámetros de la regresión lineal rd=bP-m
Una vez determinados los parámetros, se simula el modelo que ofrece una aproximación de la fluctuación poblacional de la presa y su depredador, donde lo más importante es calcular el punto de equilibrio P*=m/b D*=r/a para conocer el nivel de densidad del depredador que permite mantener a la presa en un nivel estable.
Al Modelo de Lotka-Volterra se le hicieron diferentes modificaciones; entre las más importantes aparecen las realizadas por el Grupo de Matemática de la Universidad de Xinyang de China, en trabajo multidisciplinario con el Instituto de Control Biológico de Beijing, informando un modelo que incluye el insecto trasmisor de una enfermedad (Infectado) y el no trasmisor (Susceptible) en interacción con el depredador (23). Otro modelo predice los cambios de fluctuación de poblaciones susceptibles e infectadas cuando existen perturbaciones ambientales o de otra índole (24). Investigadores chinos también desarrollaron un modelo modificado que incluye la respuesta funcional del depredador en competencia con un segundo depredador (25, 26).
También se debe señalar que el estudio de estabilidad del Modelo Lotka-Volterra generalizado, que incluye la interacción de n especies, fue matemáticamente esbozado por investigadores de la Universidad de Chester, en Inglaterra (27), quienes con anterioridad exploraron, con este tipo de modelo, la modificación de la tasa de adaptación de una plaga en cultivos resistentes (28). Todo ello permitió identificar al modelo presa-depredador, como un patrón inicial para estudios de los sistemas dinámicos.
Modelo de Competencia interespecífica
Para conocer si existe en el ecosistema un desplazamiento competitivo de una especie por otra, se emplea un modelo basado en el principio de competencia formulado por Grinnell en 1904 y replanteado por Sharov en 1999 (2):
«No es probable que dos especies de aproximadamente los mismos hábitos de alimentación permanezcan en un equilibrio uniforme en la misma región. Una desplazará a la otra de acuerdo a las condiciones locales, solo una sobrevivirá a la aparición de cualquier invasor».
Bajo el principio de que cada organismo compite con todos los individuos, la tasa de crecimiento de una población está determinada por la suma de los individuos de ambas poblaciones y el modelo de competencia se representa por un sistema de dos ecuaciones diferenciales:
Donde:
K1, K2: densidades máximas de las poblaciones 1 y 2, respectivamente
r1, r2: tasas intrínsecas de incremento.
w1, w2: coeficientes de competencia, efecto de una especie sobre la otra. Si se desconocen estos valores, se pueden tomar como 0,5 admitiendo igual efecto competitivo.
Los parámetros K y r para ambas poblaciones se determinan empleando el modelo de crecimiento logístico.
Además de la simulación de la dinámica, es importante graficar las isóclinas, estas son la recta ![]() que pasa por los puntos (K1;0) (0; K1/w1) y la recta
que pasa por los puntos (K1;0) (0; K1/w1) y la recta ![]() que pasa por los puntos (K2/w2;0) (0; K2) . Si estas rectas se cortan, existe un equilibrio estable y las especies coexisten. De lo contrario, una especie es excluida por la otra (29).
que pasa por los puntos (K2/w2;0) (0; K2) . Si estas rectas se cortan, existe un equilibrio estable y las especies coexisten. De lo contrario, una especie es excluida por la otra (29).
Modelo Hospedante-Parásito o Parasitoide
Tanto el parásito como el parasitoide, son especies que realizan su ciclo de vida en relación con el hospedante, pero pueden o no ocasionarle la muerte. En consecuencia, los modelos que se simulan para predecir la dinámica de estas poblaciones difieren de los modelos presa -depredador (2). En este sentido, los modelos más empleados son el Modelo de Thompson de 1929 (30), el Modelo de Nicholson y Baley de 1935 (31), el Modelo de Rogers de 1972 (32) y el Modelo de Anderson y May de 1981 (22).
Donde.
H: Densidad del hospedante
P: Densidad del parasitoide
F: Tasa de fecundidad del parasitoide (número de huevos que pone una hembra)
R: Reproducción promedio del hospedante
q: Proporción de hembras del parasitoide
De ello se puede estimar el número promedio de huevos que pone un parasitoide en contacto con un hospedante: ![]()
Este modelo supone que todos los huevos que pone el parasitoide eclosionan. Este supuesto implica habilidad de búsqueda ilimitada del parasitoide. Por lo cual, se dice que el Modelo de Thompson puede sobrestimar la tasa de parasitismo, sobre todo si la densidad del hospedante es baja.
Siendo F=aH. Las variables y parámetros son los mismos que en el Modelo de Thompson, pero note que en esta nueva forma de escribir el modelo la fecundidad potencial del parásito no está limitada. Los parásitos ponen un huevo por cada encuentro con el hospedante, aun cuando el número de encuentros sea muy grande. Este modelo tiende a sobrestimar el porcentaje de parasitismo cuando la densidad del hospedante es alta.
Fmax se obtiene a partir del Modelo de Respuesta Funcional de Holling (33), si se define:
En la naturaleza, el sistema hospedante-parasitoide nunca muestra oscilaciones de amplitud infinitamente creciente. Esto se observa en la representación de la dinámica de estos modelos, porque no incluyen mecanismos de competencia intraespecífica que puedan parcial, o completamente, lograr la estabilidad del sistema. También, hay que tener en cuenta la heterogeneidad espacial y dispersión del parasitoide. Considerando estos aspectos fue propuesto el Modelo Anderson y May de 1981 (22):
Las variables se definen como:
X: densidad de hospedantes sanos
Y: densidad de hospedantes parasitados
H = X+Y
W: densidad del parásito.
Los parámetros se definen como:
r: Tasa de crecimiento del hospedante r=a-b
a: Tasa de multiplicación del hospedante
b: Tasa de mortalidad del hospedante
a: Mortalidad del hospedante inducida por parasitismo
v: Tasa de variación de infectado a infectivo
g: Tasa de recuperación
l: Número de descendientes del hospedante producido por contacto con el hospedante.
m: Tasa de mortalidad del parasito
El Modelo Anderson y May incluye la separación del hospedante sano del parasitado y ofrece una interpretación fiable de los efectos de regulación entre el parásito y el hospedante. Sin embargo, no permite describir la dinámica de las diferentes fases del hospedante y tampoco incluye la relación con el cultivo afectado. Modelos más completos, que incluyen la dinámica del cultivo, se propusieron y se logró una mejor predicción (34). Por esto se aconseja plantear el sistema en cuestión con el mayor número de consideraciones para facilitar un mejor pronóstico de la densidad de las poblaciones hospedante-parásito o parasitoide.
MODELOS CUBANOS DE PREDICCIÓN EN EL CAMPO DE LA SANIDAD VEGETAL
En primera instancia, los matemáticos tratan de emplear técnicas estadísticas que le permitan buscar relaciones causas-efecto y que ofrezcan un pronóstico global, ya sean regresiones lineales o no lineales (35), incluyendo métodos como el análisis de componentes principales, que permitan obtener la relación de la densidad poblacional con los componentes del clima (36). Para estos estudios, es imprescindible tener en cuenta la correspondencia entre la fecha de muestreo y los datos climáticos que se empleen, así como que estos se tomaron a no más de 1 km del lugar de muestreo; de lo contrario los resultados no serán muy confiables.
Se reconoce que para estudiar la dinámica de una enfermedad transmitida por vectores es mucho más eficiente emplear ecuaciones diferenciales (37). Los modelos presa-depredador continúan siendo los más recomendados en los estudios de interacciones que acontecen en los ecosistemas (23). Entre los modelos cubanos desarrollados en este sentido está la modificación del modelo presa-depredador que incorpora componentes del clima, el cual fue validado en la modelación del crecimiento del ácaro Tetranychus urticae (38) y la inclusión de más de un depredador presentado como modelo presa - dos depredadores (39). También, ha sido práctica común desarrollar modelos que incluyan al cultivo (40).
RETOS DE LA BIOMATEMÁTICA EN CUBA
En los últimos años, muchos investigadores se interesaron en la posibilidad de predecir los sucesivos eventos que tienen lugar a lo largo del ciclo de vida de los insectos. Igualmente, se ha convertido en un estudio de vital importancia conocer cómo estos eventos están relacionados con el cambio climático. La biomatemática debe encaminar sus investigaciones hacia la búsqueda de modelos para predecir la dinámica de las poblaciones que afectan a cultivos de importancia económica, en virtud de establecer adecuadas estrategias para el manejo de plagas. En tal sentido, se señalan en este trabajo algunas consideraciones, que en nuestra opinión deben recibir atención prioritaria:
- Continuar con el empleo del modelo lineal general y la metodología de superficie respuesta para estudios relacionados con la definición de dosis, frecuencia, momento de aplicación, fiabilidad y compatibilidad con otros productos (41,42).
- Mantener el empleo de técnicas de la estadística multivariada con la finalidad de identificar los factores que inciden, de manera positiva o negativa, en el incremento de un vector (43).
- Elaborar modelos determinísticos y validarlos a partir de parámetros poblacionales estimados experimentalmente. Validar el nivel de predicción de estos modelos con datos de campo (44, 45).
- Incorporar en la toma de decisiones los estudios de riesgo y vulnerabilidad por plagas, en correspondencia con las estrategias de adaptación al cambio climático. Incluir estudios de escenarios climatológicos apoyados en el uso de sistemas de información geográfica (46).
- Elaborar modelos de pronóstico a partir de estudios geoestadísticos que incorporen análisis de dispersión de las plagas (47).
- Incorporar la estadística bayesiana en los estudios de predicción de relaciones causales (48).
Los elementos recogidos en este estudio evidencian los resultados obtenidos por Cuba en la biomatemática, dirigidos al pronóstico de la dinámica de poblaciones. Se muestran los retos que deben enfrentar los equipos multidisciplinarios, en aras de lograr un mayor conocimiento de las poblaciones plagas y sus enemigos naturales. Estos constituyen elementos vitales para establecer estrategias encaminadas al manejo de las poblaciones y la producción de alimentos sanos, en el contexto de adaptación al cambio climático.
REFERENCIAS
1. Edelstein-Keshet L. Mathematical Models in Biology. 2004; http://es.wikipedia.org/wiki/Especial:FuentesDeLibros/0075549506 . ISBN 0-07-554950-6.
2. Sharov A. Quantitative Ecology Population. 1999. Consultada 16-5-2014. Disponible en: http://www.ento.vt.edu/~sharov/PopEcol/.
3. Lotka A. Elements of physical biology. 1928; eds Baltimore: Williams & Wilkins Co. 321pp.
4. Levins R., Miranda I. Mathematical models in crop protection. Rev Protección Veg. 2007;22(1):1-17.
5. Marco V. Modelización de la tasa de desarrollo de insectos en función de la temperatura. Aplicación al Manejo Integrado de Plagas mediante el método de grados-día. Entomología Aplicada. 2001;28(7):147-150.
6. Wagner TL, Wu H, Sharpe P, Schoolfield RM, Coulson RN. Modeling insect development rates: a literature review and application of a biophysical model. Ann Entomol Soc Am. 1984;77:208-225.
7. Pedigo L. Entomology and pest management. 1996; 2nd Edition. Ed. Prentice-Hall Inc. New Jersey. 679 pp.
8. Domínguez IM. Cálculo de temperaturas extremas para insectos (Arthropoda: Insecta) en condiciones de laboratorio. Centro Agricola. 2006;33(3):91-92.
9. Sanderson ED, Peairs LM. The relation of temperature to insect life. N. H. Coll. Agric Exp Stn. 1913;7:25-41.
10.Arnold CY. Maximum-minimum temperatures as a basic for computing heat units. Proc Am Soc Hort Sci. 1960;76:682-692.
11.Sevacherian V, Stern VM, Mueller AJ. Heat accumulation for timing Lygus control measures on a safflower-cotton complex. J Econ Entomol. 1977;70:399-402.
12.Hilbert DW, Logan JA. Empirical model of nymphal development for the migratory grasshopper, Melanopus sanguinipes (Orthoptera, Acrididae). Environ Entomol. 1983;12:1-5.
13.Lactin DJ, Holliday NJ, Johnson DL, Craigen R. An improved rate model of temperature-dependent development by arthropods. Environ Entomol.1995;24:68-75.
14.Briere JF, Pracros P, Le Roux AY, Pierre JS. A novel model of temperature-dependent development for arthropods. Environ Entomol. 1999;28:22-29.
15.Hagstrum DW, Milliken GA. Modeling differences in insect developmental times between constant and fluctuating temperatures. Ann Entomol Soc Am. 1991;84:369-379.
16.Baños HL, Alemán J, Martínez MA, Miranda I, Rodríguez H, et al. Ciclo y tabla de vida horizontal de Diaphorina citri Kuwayama (Hemiptera: Psillidae) sobre Muralla paniculata L. Rev Protección Veg. 2012;27(2):91-101.
17.Flores-Galano G, Montoya A, Rodríguez H. Biología de Raoiella indica Hirts (Acari: Tenuipalpidae) sobre Areca cataechu L. Rev Protección Veg. 2010;25(1):11-16.
18.Pérez Y, Alonso-Rodríguez D, Chico R, Rodríguez H. Biología y conducta alimentaria de Neoseiulus longispinosus (Evans) sobre Tetranychus tumidus Banks. Rev Protección Veg. 2012;27(3):174-180.
19.Duarte L, Ceballos M, Baños HL, Sánchez A, Miranda I, Martínez MA. Biología y tabla de vida de Myzus persicae (Sulzer) (Hemiptera:Aphididae) en condiciones de laboratorio. Rev Protección Veg. 2011;26(1):1-4.
20.Martínez MA, Duarte L, Ceballos M. Biología y tabla de vida vertical de Diaretiella rapae McIntosh en condiciones de laboratorio. Rev Protección Veg. 2013;28(1):23-26.
21.Benítez H. Tavisoft: software for constructing life table of arthropods. Rev Protección Veg. 2012;27(1):64.
22.Ciancio A, Mukerji KG. Modelling nematodes regulation by bacterial endoparasites. En Integrated management and biocontrol of vegetable and grain crops nematodes. 2008; SPRINGER Editor: 321-337.
23.Shi R, Jiang X, Chen L. A predator -prey model with disease in the prey and two impulses for integrated pest management. Applied Mathematical Modelling. 2009;33(5):2248-2256.
24.Wang X, Tao Y, Song X. Mathematical model for the control of a pest population with impulsive perturbations on diseased pest. Appl Math Model. 2009;33(7):3099-3106.
25.Yongzhen P, Changguo L, Shunhou F. A mathematical model of a three species prey -predator system with impulsive control and Holling Functional Response. Appl Math and Comput. 2013;219(23):10945-10955.
26.Sahabudding S, Prashanta M, Santanu R. Dynamical behavior of a two predator model with prey refuge. J Biol Phys. 2013;39(4):701-722.
27.Yibin Y, Enu-Obari N. Stabilizing a mathematical model of population system. J of Franklin Inst. 2011;348(10):2744-2758.
28.Hiller JG, Brich AN. Bi-trophic mathematical model for pest adaptation to a resistant crop. J theoretical boil. 2002;215(3):305-319.
29.Suris M, Pérez JC, Miranda I. Competencia interespecífica entre Heliothis virescens (F.) y Spodoptera frugiperda Smith (Lepidoptera: Noctuidae) en el cultivo del garbanzo (Cicer arietinum L.) Rev Protección Veg. 2013;28(3):171-177.
30.Thompson WR. On the relative value of parasites and predators in the biological control of insect pests. Bull Entomol. 1929;19:343-350.
31.Nicholson AJ, Bailey VA. The balance of animal populations. Proceedings of the Zool Soc of London.1935;1:551-598.
32.Rogers DJ. Random search and insect population models. J Animal Ecol. 1972;41:369-383.
33.Rakhshani E, Talebi A, Kavallieratos N, Fathipour Y. Host stage preference, juvenile mortality and functional response of Trioxys pallidus (Hymenoptera: Braconidae, Aphidiinae). Biologia, Bratislava. 2004;59(2):197-203.
34.Baños HL, Martínez M, Miranda I. Modelling host-parasitoid interaction in the system Diaphorina citri Tamarixia radiata on Muralla paniculata. International J of Math Sci & Engg Appls. 2013;7(1):1-14.
35.Jimenez SF, Reyes S, Cortinas J, Roscandi J, Vazquez M. Dinámica de la población Thrips tabaci Livdeman (Thysanoptera:Thripidae) en ajo (Allium sativum L.). Fitosanidad. 1999;3(1):21-30.
36.Murgido C, Vera R. Influencia de algunos factores del ambiente sobre la población de mosca blanca (Bemisia spp.) en tomate de crecimiento intermedio. Fitosanidad. 1999;3(1):7-10.
37.Basañez MG, Rodríguez D. Dinámica de la transmisión y modelo matemático en enfermedades transmitidas por vectores. Entomotropica. 2012;19(3):113-134.
38.Miranda I, Ramos M. Mathematical study of the growth of Tetranichidae mites under field conditions. Relationship prey -predator. Applied Numerical Mathematic. 2002; 40:137-142.
39.Miranda I, Herrera D, Valenciaga N, Lopez M, Fernández M. Modeling of the interaction prey -two predators for the Heteropsylla cubana -Chilocurus cacti - Chrysoperla sp. system. Cuban J Agr Sci. 2007;41:295-298.
40.Miranda I, Baños H, Martínez MA, Alemán J. Modelo teórico de la interacción de Diaphorina citri Kuwayana (Hemiptera: Psyllidae) con sus enemigos naturales. Rev Protección Veg. 2008;23(2):126-130.
41.Miranda I, Arévalo J, Hidalgo L. Metodología de superficie respuesta para evaluar estabilidad en almacén de un agente de control biológico. Rev Protección Veg. 2013;28(3):224-228.
42.Reilly JR, Elder B. Effects of biological control on long-term population dynamics: identifying unexpected outcomes. J Appl Ecol. 2014;51:90-101.
43.Martínez Y, Martínez MA, Quiñones M, Miranda I, Holt J, Chancellor T. Estudio de factores que influyen en la epifitología del complejo mosca blanca-geminivirus en la región oriental de Cuba. Rev Protección Veg. 2009;24(1):47-50.
44.Baños H, Miranda I, Martínez MA. Modeling host-parasitoid interaction in the system Diaphorina citri- Tamarixia radiata on Muralla paniculata. International J of Math Sci & Engg Appls. (IJMSEA). ISSN 0973-9424. 2013;7(1):1-14.
45.Miranda I, Gómez L, Benítez H, Castillo Y, Hernández-Ochandía D, Rodríguez MG. A mathematic model for the interaction between Meloidogyne spp. and Pasteuria penetrans. Rev Protección Veg. 2014;29(2):145-149.
46.Arriagada V. Metodología para construir perfiles de peligro fitosanitario de plantas, productos vegetales y otros artículos reglamentados / IICA - San José, C.R. ISBN13: 978-92-9248-124-7. 2009; 96 p.
47.Ortiz BV, Perry C, Goovaerts P, Vellidis G, Sullivan D. Geostatistical modeling of the spatial variability and risk areas of southern root-knot nematodes in relation to soil properties. Geoderma. 2010;156:243-252.
48.Rouder J, Morey R. Default Bayes factors for model selection in regression. Multivariate Behavioral Research. 2012;47(6):877-903.
Recibido: 15-10-2014.
Aceptado: 13-11-2014.