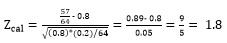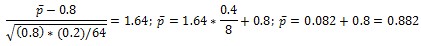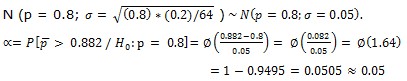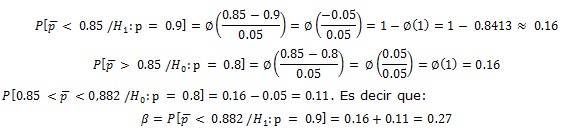Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
En el programa de la asignatura de Bioestadística de la carrera de Medicina, 1) se fundamenta el propósito de la asignatura, la cual prepara a los estudiantes en la recogida, procesamiento, presentación e interpretación de los datos de salud, al hacer un uso eficiente de herramientas estadísticas diseñadas para este fin. 2,3,4,5
Se enfatiza lo importante de llevar al entendimiento de los estudiantes la necesidad de identificar cuándo necesita ayuda de un especialista en bioestadística, según las recomendaciones recibidas por este e interpretar los resultados producto del procesamiento estadístico básico. 1
Esta asignatura se complementa y enriquece con la utilización de las habilidades adquiridas en la asignatura precedente de esta disciplina, a través del uso de las tecnologías y las redes, como herramienta de trabajo. Los contenidos definidos constituyen también sustento metodológico de la estrategia curricular de investigaciones e informática y las habilidades desarrolladas en esta asignatura se refuerzan mediante las tareas previstas en la ejecución de la estrategia. 1
En el análisis de los objetivos generales propuestos en el programa de la asignatura Bioestadística, 1 se destacan entre otros:
Desarrollar la capacidad organizativa y el hábito de proceder reflexivamente en el enfrentamiento de los problemas relacionados con el tratamiento metodológico, estadístico y computacional de la información de salud. Interpretar los fundamentos de la teoría de las probabilidades y el muestreo como sustento de la Inferencia estadística.
Analizar el propósito de la Inferencia estadística y de sus ramas: Estimación y Prueba de hipótesis en el proceso de investigación científica. 1
Diferenciar a través de ejemplos el problema de estimación y el problema de prueba de hipótesis. Interpretar el nivel de confianza y el nivel de significación en el contexto de ejemplos sencillos de aplicación en problemas de estimación y prueba de hipótesis en el campo de las ciencias médicas. Interpretar resultados de la aplicación de técnicas de inferencia estadística. 1
El sistema de habilidades que presenta el programa responde a: Interpretación de los conceptos básicos de probabilidades y muestreo. Diferenciación entre la Estadística descriptiva y la Inferencia estadística. Interpretación de las funciones de la Inferencia estadística. Diferenciación entre los problemas de estimación y prueba de hipótesis. 1
Al profundizar en los objetivos del tema de Estadística Inferencia se muestra una correspondencia con los objetivos generales de la asignatura, así como los contenidos propuestos en cuestión, elemento que precisa la revisión de las orientaciones metodológicas sobre el tema, donde se destaca:
Hacer hincapié en los aspectos conceptuales y generales en casos concretos de aplicación de técnicas de la inferencia estadística en la investigación biomédica sin detenerse en fórmulas ni métodos específicos, las actividades deben estar orientadas a responder qué es, cuándo y por qué se utiliza, cómo se interpreta su resultado y qué significado tiene para el conocimiento. 1
No se comparte la orientación dado su cumplimiento estricto, porqué para hacer hincapié, insistir con firmeza, perseverar y empeñarse es profundizar en el conocimiento en aspectos conceptuales y generales, en casos concretos de aplicación de las técnicas de la inferencia estadística en la investigación biomédica, luego se plantea sin detenerse en las fórmulas, los métodos específicos, las actividades deben estar orientadas a responder qué es, cuándo y por qué se utiliza, cómo se interpreta su resultado y qué significado tiene para el conocimiento.
Para responder estas interrogantes es necesario dominar, los conceptos y definiciones, los métodos, los procedimientos, los algoritmos, los cuales facilitan la interpretación del problema que se resuelve. 1) Esta orientación se contrapone a los objetivos generales y por temas, así como a las habilidades descritas en el programa de la asignatura.
Utilizar como ejemplos aquellos que involucren parámetros y estadígrafos conocidos por los estudiantes como son la media aritmética y la proporción o el porcentaje de las variables de interés. Estos ejemplos deben ser seleccionados por su simplicidad y la importancia de los resultados extraídos de la literatura científica disponible. 1 Se asume la importancia que tiene estas variables y las relaciones a establecer, desde los componentes: académico, laboral e investigativo. 6
Se sugiere al profesor que cree un banco de aplicaciones donde se utilicen técnicas de Inferencia estadística, de forma tal que pueda distribuir a los estudiantes para que valoren la importancia de aplicar dicha técnica en casos precisos y como su resultado de la interpretación en la toma de decisiones. 1
Se consideran orientaciones necesarias, precisas e importantes a tener en cuenta por parte de los profesores de esta asignatura y el estricto cumplimiento de todas; por otra parte no se limitan la creación y las potencialidades de los estudiantes de la carrera de Medicina, se alienta la capacidad creativa de los profesores y estudiantes.
En general se precisan y se aclaran orientaciones y regulaciones importantes para el desarrollo óptimo del plan de estudio de la carrera de Medicina, lo cual genera necesidades a resolver desde el punto de vista didáctico y científico-metodológico.
En el proceso de enseñanza aprendizaje (PEA), no se deben fijar patrones en la forma de proponer y resolver los ejemplos, los ejercicios, y los problemas para evitar estereotipos, los cuales se trasmiten entre los profesores de una disciplina durante años, basado en los resultados obtenidos.
El propósito del trabajo: ilustrar a través de la resolución de problemas de la estadística inferencial como estimular el pensamiento creativo de los profesores de Bioestadística y los estudiantes de la carrera de Medicina.
Métodos
Se emplean los métodos teóricos: análisis-síntesis, inducción-deducción, abstracción-concreción. El método para construir curvas de funciones elementales, 6,7,8,9 procesos de comprensión, explicación e interpretación. Se aplican métodos, procedimientos y algoritmos matemáticos y estadísticos.
Los métodos empíricos aplicados se enmarcan en la observación participante y no participante, a fin de profundizar en el problema y obtener información sobre las dificultades principales que afectan el proceso de enseñanza aprendizaje, a partir de las clases, como formas de organización docente.
Se desarrollan talleres de socialización para valorar la viabilidad de la efectividad de la alternativa didáctica propuesta.
La población está constituida por 21 profesores de la asignatura Bioestadística del primer año de la carrera de Medicina, se realizaron 15 visitas a clases al azar. Se revelan en las actividades docentes desarrolladas por el colectivo de profesores las siguientes dificultades:
- No siempre se propician en las diferentes actividades docentes variantes en la manera de analizar y utilizar los conceptos estudiados en función de estimular el pensamiento creador en problemas que así lo exigen.
- No existe una estrategia de trabajo para profundizar en alternativas que desarrollen capacidades creativas en los estudiantes, las cuales se apoyen en programas informáticos profesionales para visualizar los resultados e interpretarlos.
- Es insuficiente la utilización de paquetes estadísticos profesionales.
- No existe un banco de problemas que rompa con los esquemas de la enseñanza tradicional de la estadística inferencial.
Se efectúa una revisión documental del programa de la disciplina y la asignatura, en general el plan de estudio de la carrera de Medicina, revisión científica de libros y artículos referente al tema: Introducción a la estadística inferencial.
Resultados
A continuación se propone analizar la solución de los siguientes problemas, los cuales se orientan previamente, como trabajo independiente, lo cual garantiza la participación activa y creativa de los estudiantes: 10,11,12
Problema 1. Los datos contenidos en la certificación técnica de un medicamento muestran su efectividad en el 80 % de los casos para curar cierto tipo de dermatitis. Como resultado de las modificaciones de la terapéutica, se espera un aumento de la efectividad del mismo. Para verificar esta afirmación se efectúan comprobaciones se seleccionan al azar 64 pacientes, de ellos resultaron curados 57 con modificaciones en el tratamiento.
Se supone que la muestra de los pacientes se ha obtenido, a partir de una población madre distribuida normalmente cuya proporción es P0=0.80, cuya varianza es: σ2=0.0025; es decir N (p=; σ2=0.0025). Utilice el criterio de significación para verificar la hipótesis: Las modificaciones de la terapéutica no ejercen influencias en el aumento de la efectividad del medicamento. Utilice un nivel de significación del 5 %.
Problema 2. Considere válidos los datos del ejercicio anterior, al suponer que junto a la hipótesis H0: p=0.8, se examina la hipótesis alternativa H1: p=0.9. En calidad de estadística del criterio se toma la proporción muestral /. Se sabe del problema 1 que el dominio crítico está dado por la desigualdad p >0.882.
Determine la probabilidad de los errores de primer y segundo géneros α y β para el criterio del dominio crítico.
Es posible elaborar para el estudio independiente problemas que modelan el comportamiento de la efectividad de un medicamento seleccionado, con una significación del 0.01 (1 %); escoger al azar una muestra grande (conveniente).
En general incluir situaciones de salud para distribuciones normales (distribuciones de medias aritméticas) de forma análoga.
La simulación de las situaciones se considera de gran ayuda para comprender, explicar e interpretar estas (Tabla 1).
Tabla 1 Errores de primer y segundo género, según la decisión de rechazar y no rechazar H0
| Si H0 es: | Decisión sobre H0 | |
| Rechazar | No Rechazar | |
| Verdadera | Error Tipo I (α) Problema |
Acción Correcta |
| Falsa | Acción Correcta | Error Tipo II (β) Problema 2 |
El colectivo de profesores de Bioestadística, a partir del banco de problemas creado para desarrollar el tema: Introducción a la estadística inferencial. Propone una estrategia para analizar y utilizar los conceptos estudiados en el tema, en función de estimular el pensamiento creador en problemas que así lo exigen.
Las alternativas para desarrollar capacidades creativas en los profesores y estudiantes, los problemas a elaborar deben apoyarse en situaciones de salud a enfrentar por el Médico General, cuyos resultados e interpretaciones se visualicen, mediante programas informáticos profesionales, los cuales se orientan como tareas docentes a desarrollar en el estudio independiente.
Problema 3. Se considera una población conformada por el Adulto Mayor perteneciente a un Policlínico, el promedio de pulsaciones por minutos es de 80, estas se registran antes de realizar ejercicios físicos sistemáticos. Seis meses después, se seleccionan 25 adultos mayores al azar, el promedio de las pulsaciones es de 78 pulsaciones por minutos y desviación estándar de cuatro pulsaciones por minutos.
1. Plantee las afirmaciones H0 y H1.
2. Determine la probabilidad de los errores de primer y segundo géneros (α y β) para el criterio del dominio crítico.
3. Describa el comportamiento del promedio de las pulsaciones por minutos del Adulto Mayor en la población que practican ejercicios físicos sistemáticos en el Policlínico, según las evidencias analizadas (problema propuesto para el estudio independiente).
Discusión
Solución del problema 1: 1) Se comprueba la hipótesis.
H0: p=0.8. Se aplica la terapéutica clásica, la cual no ejercen influencias en el aumento de la efectividad del medicamento.
H1: p>0,8. Se aplica la terapéutica modificada, la cual ejerce influencia en el aumento de la efectividad del medicamento.
2) Se selecciona α =0.05
3) (e1):
4) Ztab=1.64. Como el valor muestral de la estadística del criterio (el estadígrafo) pertenece al domino crítico (Ztab =1.64<Zcal =1.8). La hipótesis nula se rechaza:
Conviene suponer que las modificaciones de la terapéutica causan (originan) un aumento de la efectividad del medicamento con nivel de significación de 0.05 (5%).
La frontera / del dominio crítico para la estadística inicial X (Variable aleatoria para proporciones) del criterio puede ser obtenida a partir de la relación (e2):
De donde se obtiene p¯>0.882, o sea, el dominio crítico la estadística (estadígrafo) / está definida por la desigualdad 𝑝 >0.882. Lo que significa que cualquier muestra de estudio, cuya proporción muestral resulte mayor 0.882, difiere de la proporción poblacional P0=0.80; con nivel de significación 5 % (α=0.05).
Solución del problema 2:
La probabilidad del error de primer género. La estadística / del criterio, a condición de que sea cierta la hipótesis H0: p =0.8, es una distribución normal (e3):
De acuerdo con el criterio aceptado, significa que el 5 % de los medicamentos con efectividad del 80 %, se clasifican con el 90 % de efectividad.
A condición de que sea justa la hipótesis alternativa H1: p=0.9, la estadística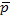 
tiene distribución normal N (p=0.9; σ=0.05). La probabilidad del error de segundo género es igual a (e4):
Según la representación de las densidades de las distribuciones de probabilidad normal de las proporciones de la efectividad del medicamento y su aumento mediante modificaciones en la aplicación de la terapéutica: N (p=0.8; σ=0.05) y N (p=0.9; σ=0.05), 4,5) (e5):
De acuerdo con el criterio aceptado, significa que el 27 % de los medicamentos con efectividad del 90 %, se clasifican con el 80 % de efectividad.
Las probabilidades de los errores de primero y segundo géneros se muestran a continuación y se conforman por las curvas (Figura 1): 13,14,15
1
Figura 1 Modelo matemático (estadístico) está representado por las densidades de la distribución probabilística normal de la proporción (de la efectividad del medicamento para curar cierta dermatitis): N (p = 0.8; σ =0.05), en color rojo y el aumento de la proporción, mediante modificaciones en la aplicación de la terapéutica: N (p = 0.9; σ =0.05), color azul.
Se ha modelado el comportamiento de la variable aleatoria X1: Proporción (p) de la efectividad de un medicamento para curar cierto tipo de dermatitis y X2: Proporción del aumento de la efectividad del medicamento en determinadas condiciones.
¿Cuál es la afirmación general, desde el punto probabilístico acerca del comportamiento de las variables aleatorias que se describen en el fenómeno de estudio, es decir la tendencia de las proporciones, según la efectividad del medicamento para curar cierto tipo de dermatitis?
El 95 % de los medicamentos poseen una efectividad del 80 %; pero el 5 % de estos sobrepasan esa efectividad de manera natural. Si se aplican modificaciones en la aplicación de la terapéutica al total de los medicamentos con efectividad del 80 %, el 27 % no alcanzan el 90 % de efectividad.
Se simula el comportamiento de un lote de 10 000 unidades, según el modelo matemático (modelo probabilístico) que lo representa, lo simboliza, lo significa y lo interpreta.
Resultan efectivas: 8 000 unidades; no efectivas: 2 000 unidades, es decir en realidad curan 8 000 unidades, de ellas 400 unidades sobrepasan el 80 % de efectividad. El 27 % de 8000 unidades es: 2 160 unidades, las cuales no alcanzan el 90 % de efectividad, a pesar de las modificaciones en la terapéutica. Es decir: 8 000-2 160=5 840 unidades alcanzan el 90 % de efectividad con modificaciones en la terapéutica.
Conclusiones
Es importante crear situaciones de salud a enfrentar por el Médico General en su quehacer profesional que evidencien las necesidades de interpretar los errores de primero y segundo género: α y β, de esta manera se consolidan los conocimientos y habilidades relacionadas con los conceptos abordados en el tema: Introducción a la estadística inferencial del programa de la asignatura Bioestadística del primer año de la carrera de Medicina.
Se ilustra a través de las soluciones de problemas sencillos los resultados de la aplicación de técnicas de la estadística inferencial en situaciones biomédicas, las interpretaciones y los resultados, se visualizan mediante los conceptos: variable aleatoria, distribución normal, probabilidades, dominio de aceptación, dominio de rechazo, estimaciones puntuales, entre otras.
Los objetivos propuestos en este programa y las orientaciones metodológicas, no constituyen limitantes para estimular el pensamiento creativo de profesores y estudiantes, sino que incitan a desarrollar y estimular estas capacidades mentales, dado el carácter bilateral del proceso de enseñanza aprendizaje.
Se recomienda realizar talleres metodológicos y colectivos con los profesores de las asignatura Bioestadísticas para diseñar alternativas en función de estimular el pensamiento creador en la elaboración de un banco de problemas, donde se utilicen técnicas de inferencia estadística, mediante programas informáticos profesionales para visualizar los resultados alcanzados, según la modelación y la simulación matemática, en función de comprender, explicar e interpretar la solución de estos problemas
