INTRODUCCIÓN
Las producciones de la industria biofarmacéutica se han hecho gradualmente dependientes de procesos a gran escala que usan cultivos de células de mamíferos.1 La línea celular de células de ovario de hámster chino (Chinese Hamster Ovary, CHO) es la más empleada en la industria biotecnológica, sirviendo de base para la producción de más del 70% de las proteínas recombinantes, la mayoría de ellas anticuerpos monoclonales.2 Esta línea celular es fuente de obtención de una gran variedad de proteínas de alto valor terapéutico como la Eritropoyetina Humana Recombinante (EPOhr), hormona glicoproteica que al aumentar la cantidad de glóbulos rojos es utilizada de forma efectiva en el tratamiento de la anemia severa. Desde el año 1985 este es un fármaco que se utiliza para el tratamiento de la anemia por insuficiencia renal crónica; sin embargo, últimamente ha tenido otras aplicaciones en anemias asociadas a patologías no renales, como la anemia asociada a cáncer y pacientes con VIH.
Una vez que la producción de un biofármaco ha sido aprobada, cualquier desviación significativa del protocolo de producción puede requerir nuevas pruebas clínicas para probar la seguridad del producto resultante. Como las pruebas clínicas son muy caras, las mejoras del proceso son llevadas a cabo bajo restricciones muy fuertes; de aquí que los procesos de producción sean operados normalmente con parámetros alejados de sus valores óptimos.3
El proceso productivo de obtención de la EPOhr tiene potencialidades para su mejora.4 Dicho proceso consta de dos secciones fundamentales: una etapa de fermentación seguida de una etapa de purificación en columnas cromatográficas, similar a los procesos de obtención de vacunas como Heberbiovac HB® contra la hepatitis B y la vacuna CIMAvax-EGF® contra el cáncer de pulmón.5,6 En el caso estudiado, la fermentación tiene lugar en biorreactores de tanque agitado que operan en modo perfusión, los que pueden lograr altas concentraciones del producto y altas productividades volumétricas. La etapa de purificación está basada en cuatro pasos cromatográficos, los cuales usan cromatografía de afinidad, cromatografía de intercambio iónico y cromatografía de exclusión molecular.4
En la planta de producción de EPOhr ha habido una gran variabilidad en los rendimientos de la etapa de purificación. A pesar de que existe una gran cantidad de información registrada, ha faltado conocimiento con relación a la forma en que las variables controladas impactan los rendimientos de purificación.
El análisis de datos multivariantes tiene una gran potencialidad para la mejora de las producciones biofarmacéuticas.7 Dicho análisis puede combinarse con otros métodos y técnicas para lograr una comprensión mejor del proceso y ejercer un control de su calidad. Los procesos de la industria biofarmacéutica típicamente generan conjuntos grandes de datos multivariados, los cuales se caracterizan por ser muy heterogéneos, correlacionados y no lineales por naturaleza, así como por tener altos niveles de redundancia y ruido. En este sentido la utilidad de las técnicas de análisis de datos multivariantes ha sido probada en el área de la industria biofarmacéutica. Su habilidad para reducir dimensionalidad, removiendo la redundancia y el ruido, permite identificar las características más sobresalientes de los datos. Estas características pueden ser después utilizadas en el monitoreo de los bioprocesos, la detección de fallas y la optimización, lo cual ha sido descrito extensamente en la literatura.1,3
Los detalles internos de la mayoría de los procesos de la industria biofarmacéutica no son bien comprendidos, lo cual dificulta el desarrollo de modelos fenomenológicos, de aquí que para muchos de estos procesos sea necesario confiar sustancialmente en el desarrollo de modelos orientados a datos. Para el desarrollo de este tipo de modelos, la disponibilidad cada vez más creciente de datos registrados, tanto en línea como fuera de línea (espectroscópicos o de otro tipo), brinda a los especialistas una información sustancial como punto de partida para el análisis multivariante.8
Un método de análisis multivariante de gran utilidad para explicar las fuentes de variabilidad de un proceso y reducir dimensionalidad de los datos, es el Análisis de Componentes Principales (ACP). Este método transforma la información multidimensional en unas pocas variables que explican una gran parte de las fluctuaciones de las variables originales, así como sus interrelaciones.9 Dada la gran cantidad de datos experimentales disponibles en la planta del caso estudiado, se decidió aplicar este método y de esta manera fue posible extraer información útil para la toma de decisiones, sin necesidad de disponer de un modelo teórico sobre el comportamiento del proceso.
La cromatografía ha tenido un gran desarrollo y de técnica analítica ha pasado a ser un proceso de separación bien establecido en la industria. En la literatura se han reportado aplicaciones industriales a gran escala en diversos campos como: la industria petroquímica, la industria de alimentos y la industria biofarmacéutica. El ACP ha sido ampliamente utilizado en la evaluación de columnas cromatográficas.10,11,12,13,14,15,16 En los casos reportados su aplicación se ha limitado al nivel de operación de una o dos columnas y no ha abarcado una etapa de purificación industrial con varios pasos cromatográficos.
El presente trabajo tuvo como objetivo realizar un ACP a los datos registrados en un período de 2 años en la etapa de purificación de una planta de EPOhr, con vistas a definir cuáles son las variables que mayor aporte tienen a la variabilidad de dicho proceso, lo cual resulta de gran interés para enriquecer la estrategia de control en esta planta.
MATERIALES Y MÉTODOS
Conjunto de datos
En la planta de EPOhr estudiada se dispone de una base de datos con los valores registrados de 55 variables pertenecientes a la operación de la etapa de purificación en un período de 2 años. Para la realización del ACP fueron 18 las variables seleccionadas como relevantes para el objetivo de este trabajo, para lo cual se partió de un estudio ya realizado con anterioridad en dicha planta;17 además, se tuvieron en cuenta consultas con expertos de la misma. De estas variables cuatro están relacionadas con el primer paso cromatográfico (cromatografía de afinidad), cinco están relacionadas con el segundo paso cromatográfico (cromatografía de afinidad) y nueve están relacionadas con el tercer paso cromatográfico (cromatografía de intercambio iónico); a continuación se presenta su explicación.
Dos variables relacionadas con el sobrenadante aplicado en el primer paso cromatográfico fueron consideradas:
1. Consumo de medio de cultivo de una célula por día (cspr, mL/célula.día), calculado como la tasa de dilución dividida entre la concentración de células vivas en el biorreactor.
2. Masa de EPOhr en el sobrenadante aplicado (masasnhplc, g), calculada con la concentración de EPOhr determinada por cromatografía líquida de alta resolución.
Las variables relacionadas con el primer paso cromatográfico, que comprende dos columnas, fueron:
3. Concentración de EPOhr en la elución de la segunda columna (concg25b, mg/mL), medida por densidad óptica.
4. Masa de EPOhr a la salida de la segunda columna (masag25b, g), calculada con la concentración de EPOhr determinada por espectrofotometría de masas.
Las variables relacionadas con el segundo paso cromatográfico fueron:
5. Relación entre la masa de EPOhr que se aplica y el volumen de gel empacado en la primera columna (masa_vgch, g/L).
6. Masa de EPOhr a la salida de la tercera columna (masag25ch, g), calculada con la concentración de EPOhr determinada por espectrofotometría de masas.
7. Relación de la densidad óptica a 280 nm entre la densidad óptica a 260 nm de la corriente que eluye en la columna (relg25ch, adim.).
8. Rendimiento del segundo paso cromatográfico (rendg25ch, %), calculado como la masa de elución de la cuarta columna dividida entre la masa de elución de la tercera columna, multiplicado por 100.
9. Rendimiento del segundo paso cromatográfico con respecto al primer paso cromatográfico (rendch_b, %), calculado como la masa de elución del segundo paso dividida entre la masa de elución del primer paso, multiplicado por 100.
Las variables relacionadas con el tercer paso cromatográfico fueron:
10. Relación de la masa de EPOhr que se aplica entre el volumen de gel empacado en la columna (masa_vgq, g/L).
11. Masa de EPOhr en el lavado de la columna (masalavq, g), calculada con la concentración de EPOhr determinada por espectrofotometría de masas.
12. Recobrado en el lavado de la columna (reclavq, %), calculado como la relación de la masa de EPOhr en el lavado entre la masa total de entrada a la misma multiplicado x 100.
13. Relación de la densidad óptica a 280 nm entre la densidad óptica a 260 nm de la corriente que eluye en la columna (releluq, adim.).
14. Masa de EPOhr en la elución de la columna (masaeluq, g), calculada con la concentración de EPOhr determinada por espectrofotometría de masas.
15. Recobrado de EPOhr en la elución de la columna (recelucq, %), calculado como la relación de la masa de EPOhr eluída entre la masa total eluída en el tercer paso multiplicado x 100.
16. Cantidad equivalente de viales después de la elución en el tercer paso cromatográfico (vialesq, adim.), calculada a partir de la masa de EPOhr que eluye en este paso.
17. Rendimiento del tercer paso cromatográfico con respecto al segundo paso cromatográfico (rendq_ch, adim), calculado como la masa de elución del tercer paso dividida entre la masa de elución del segundo paso multiplicado x 100.
18. Recobrado de EPOhr en la regeneración de la columna (recregq, %), calculado como la relación de la masa de EPOhr en la regeneración entre la masa total eluida en cada etapa de este paso cromatográfico multiplicado x 100.
De todas estas variables, nueve ya habían sido consideradas en la modelación neuronal del rendimiento de la etapa de purificación (cspr, masasnhplc, masa_vgq, recelucq, rendq_ch, concg25b, masa_vgch, rendch_b, releluq); siendo las variables cspr, masasnhplc, masa_vgq, recelucq, rendq_ch las que mayor contribución tienen al rendimiento de la etapa de purificación, medida como el rendimiento en bulbos por litro de sobrenadante (relación de la cantidad de viales obtenidos entre el volumen de sobrenadante, bulbos/L).17 Las otras nueve variables son incluidas por primera vez en el estudio (masag25b, masag25ch, relg25ch, rendg25ch, masalavq, reclavq, masaeluq, vialesq, recregq).
Análisis de Componentes Principales
El ACP es una de las técnicas estadísticas multivariantes más populares y antiguas en el análisis de datos.18 Sus principales objetivos son: extraer la información más importante de un conjunto de datos multivariantes, comprimir un conjunto de datos multivariantes manteniendo solo la información que se considere importante (reducir la dimensionalidad de los datos), simplificar la descripción de un conjunto de datos y analizar la estructura de las observaciones y de las variables.9
La idea central del ACP es reducir la dimensionalidad de un conjunto de datos consistentes en un gran número de variables interrelacionadas, reteniendo tanto como sea posible la variación de los datos originales. Esto se logra transformando las variables originales en un nuevo conjunto de variables, combinación lineal de las primarias, que se denominan componentes principales (CP), los cuales no están correlacionados entre sí y son ordenados de forma tal que el primer componente retiene la mayor parte de la variación presente en las variables originales.19
Las ecuaciones que fundamentan el método tienen la forma que se ilustra a continuación.
Los datos de partida en un ACP son los contenidos en la matriz de datos X constituida por I filas (muestras) y J columnas (variables). El proceso aborda seguidamente el cálculo de los CP. Los componentes ta (a =1,…A) serán combinaciones lineales de las variables originales Xj (j =1,…J) siendo p el peso o contribución de la variable al componente ta:
ta = pa1x1+… p aJ x J
En notación matricial:
/
En esta ecuación X es la matriz original de datos de dimensión IxJ, T es la matriz de las muestras (scores) y de dimensión IxA. La matriz P es la llamada matriz de los pesos (loadings) la cual se determina mediante los vectores propios de la matriz de covarianzas de X, tiene dimensión AxJ. P t es la transpuesta de dicha matriz. E es la matriz de los residuos con dimensión IxJ.
El número de columnas ta en la matriz T y filas pa en la matriz P, es igual al número A que es la cantidad o el número de CP que existirán. Los valores de A son menores que el número de variables J y el número de muestras I.
Normalmente, sólo los primeros CP contienen información útil, mientras que los últimos sobre todo describen ruido, cuya variabilidad no se puede explicar, por ello es útil estudiar sólo los primeros CP en lugar del conjunto de datos de partida, no sólo porque reduce la complejidad de la matriz de datos, sino también porque asegura que el ruido no es confundido con información. Lo deseable es obtener con el menor número posible de componentes, el mayor por ciento de la varianza total de los datos explicada, ya que un modelo simple es más robusto que uno complejo y más fácil de interpretar.
En el presente estudio el ACP se realizó empleando la versión 8.0 del software THE UNSCRAMBLER, el cual constituye un programa especialmente concebido para análisis multivariante de datos. Este programa permite realizar un análisis de los resultados con la ayuda de cuatro gráficos fundamentales para el entendimiento e interpretación de la información obtenida: gráfico de la varianza explicada, gráfico de la influencia, gráfico de las puntuaciones o mapa de las muestras y gráfico de los pesos o mapa de las variables.20
RESULTADOS Y DISCUSIÓN
Para el ACP se partió de una matriz con 18 variables y 201 muestras o instancias, para un total de 3618 puntos experimentales considerados.
La heterogeneidad de los datos, motivada por la presencia de variables de diferente naturaleza y diferentes magnitudes, conllevó la combinación del autoescalado y la normalización de los datos como parte del preprocesamiento, lo que facilitó la realización del análisis.
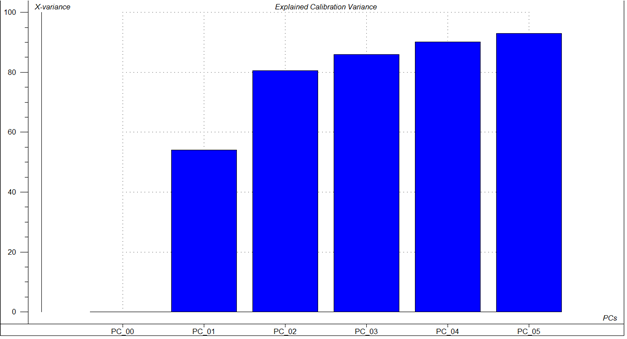
En el gráfico de la varianza explicada, que se presenta en la Figura 1, se observa que con dos CP se logra explicar más del 80% de la varianza total de los datos, lo cual es satisfactorio. El componente principal 1 (PC1) explica el 54% de la varianza, mientras que el componente 2 (PC2) explica el 27% de la varianza restante.
En el gráfico de la influencia (Fig. 2), se pueden observar muestras con elevado error residual (10 y 184) y muestras con elevado distanciamiento del comportamiento del resto de las muestras (109 y 117); estas muestras constituyen puntos discrepantes (outliers) pero no son peligrosos, por lo que no fueron eliminadas del modelo al contener información útil del proceso.
En el gráfico de las puntuaciones, representado en la Figura 3, se puede observar que la mayoría de las muestras se encuentran dentro de la elipse de Hotelling, lo cual indica que todas pertenecen a un mismo proceso, confirmando lo dicho por los especialistas de la planta de que en el período analizado no hubo diferencias significativas en el proceso de producción. Las muestras 8, 10, 11, 12, 67, 92, 109 y 117 que descansan fuera de la elipse son calificadas como puntos discrepantes (outliers) pero no son desechables, ellas responden a un comportamiento muy particular que se describe posteriormente con ayuda de la Figura 5.
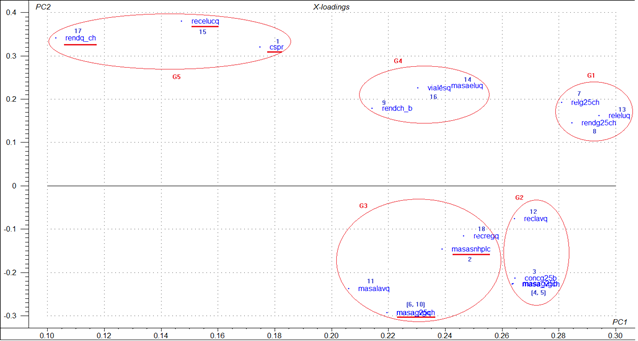
En el gráfico de los pesos, que se presenta en la Figura 4, se observa que ninguna de las variables está cercana del punto de origen de los ejes de coordenadas y todas son significativas en el aporte a uno de los dos componentes seleccionados. Se tienen agrupamientos de las variables, las que han quedado aglomeradas formando 5 grupos que se indican; de estos, los grupos del 1 al 4 contribuyen significativamente al primer componente y el grupo 5 al segundo componente.
Con relación al grupo 1, formado por las variables 7 (relg25ch), 8 (rendg25ch) y 13 (releluq):
Estas variables, por ser las que mayor aporte tienen al primer componente, son las que mayor influencia tienen en la variabilidad de los datos del proceso. Entre las mismas aparece como único rendimiento de todos los valorados el correspondiente al segundo paso cromatográfico (rendg25ch), de lo que se infiere que este es el paso más influyente; sin embargo, el mismo no constituye un control del proceso. Las variables relg25ch y releluq constituyen relaciones de densidades ópticas que se determinan, pero tampoco se controlan. Del análisis de este grupo se concluye que las variables 7, 8 y 13 deben constituir controles de proceso.
Con relación al grupo 2, formado por las variables 3 (concg25b), 4 (masag25b), 5 (masa_vgch) y 12 (reclavq):
Las variables 4 (masag25b) y 5 (masa_vgch) están altamente correlacionadas entre sí al encontrarse muy cercanas en dicho gráfico, lo que permite detectar una deficiencia operacional pues la variable 5 debería ser una variable manipulada y en realidad no lo es, estando por tanto fuera de control.
Con relación al grupo 3, formado por las variables 2 (masasnhplc), 6 (masag25ch), 10 (masa_vgq), 11 (masalavq) y 18 (recregq):
Se cumple lo mismo que en el grupo anterior pero entre las variables 6 (masag25ch) y 10 (masa_vgq), la variable 10 debería ser una variable manipulada y en realidad no lo es, estando también fuera de control. Es de destacar que las variables 2 (masasnhplc) y 10 (masa_vgq) son dos de las cinco variables que mayor contribución tienen al rendimiento en bulbos por litro de sobrenadante analizado en estudio anterior.17
Con relación al grupo 4, formado por las variables 9 (rendch_b), 14 (masaeluq) y 16 (vialesq):
Las variables 14 (masaeluq) y 16 (vialesq) están altamente correlacionadas entre sí, lo cual es lógico y era de esperar, ya que vialesq es la cantidad equivalente de bulbos que se obtiene a partir de la masa que eluye en el tercer paso cromatográfico, de aquí se infiere que a los efectos de la modelación futura, una de las variables puede ser eliminada, sugiriéndose que sea la 14.
Con relación al grupo 5, formado por las variables 1 (cspr), 15 (recelucq) y 17 (rendq_ch):
Estas son las variables que más contribuyen al segundo componente, resultando interesante que estas tres variables son las restantes de las cinco que mayor contribución tienen al rendimiento en bulbos por litro de sobrenadante analizado en estudio anterior.17
En la Figura 5 se muestra una comparación de los gráficos de las puntuaciones y de los pesos, que permite explicar el comportamiento de los puntos discrepantes anteriormente mencionados, sobre la base de que las muestras del gráfico de las puntuaciones tienen altos valores de las variables que se encuentran en el mismo cuadrante del gráfico de los pesos.
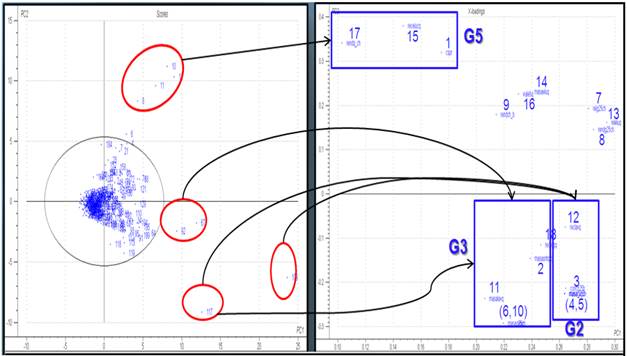
Fig. 5 Gráficos de las puntuaciones y de los pesos con las relaciones entre las muestras y las variables.
Las muestras 8, 10, 11 y 12 poseen elevados valores de las variables 1, 15 y 17 pertenecientes al grupo 5, así mismo, las muestras 67 y 92 presentan altos valores de las variables 2 y 18 del grupo 3. La muestra 109 que es la más alejada, tiene mayores valores de las variables 3, 4, 5 y 12 del grupo 2, pero tiene también altos valores de las variables 2, 6, 10, 11 y 18 del grupo 3. Finalmente, la muestra 117 es muy parecida a la 109, exhibiendo elevados valores de las variables de los grupos 2 y 3. Se comprobó con los expertos de la planta que el comportamiento alejado del resto que tienen estas muestras, se debió a cambios que se produjeron en la estrategia del proceso y cambios en el medio de cultivo.
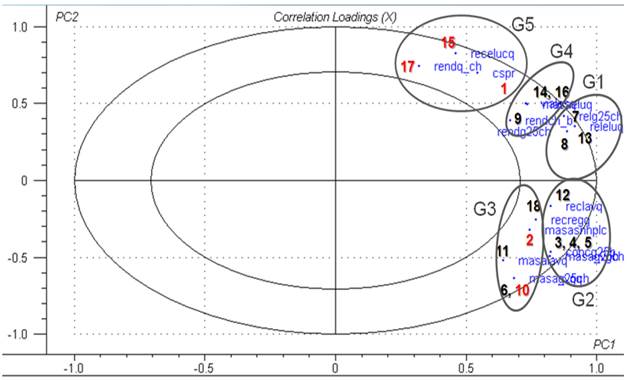
En el gráfico de los pesos de correlación (correlation loadings), que se presenta en la Figura 6, se corrobora que todas las variables tienen un aporte significativo a la variabilidad del proceso al encontrarse entre las dos elipses, y se observan los mismos agrupamientos.
Dada la gran cantidad de datos experimentales disponibles en los procesos para la obtención de productos biotecnológicos como vacunas que se purifican de forma similar a la EPOhr utilizando técnicas cromatográficas, el ACP pudiera utilizarse en dichos procesos para lograr una mayor comprensión de los mismos y enriquecer sus estrategias de control.
CONCLUSIONES
La aplicación del ACP a los datos registrados en un período de 2 años en la etapa de purificación de la planta de EPOhr estudiada, permitió definir cuáles son las variables que mayor aporte tienen a la variabilidad de dicho proceso y extraer información útil que da una mayor comprensión del proceso y ayuda a enriquecer la estrategia de control en esta planta. Dichos resultados corroboraron experiencias prácticas de sus especialistas y permitieron dar recomendaciones a considerar en el plan de verificación continuada del proceso, como proponer tres variables como controles de proceso y tener en cuenta que el rendimiento del segundo paso cromatográfico es el más influyente de los rendimientos considerados en la variabilidad.