Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
MEDISAN
versión On-line ISSN 1029-3019
MEDISAN vol.16 no.4 Santiago de Cuba abr. 2012
COMENTARIOS
Uso inadecuado de la prueba de Ji al cuadrado y la omisión del control del sesgo de confusión
Improper use of the chi-square test and the omission of the confounding bias control
MsC. Irlán Amaro Guerra
Universidad de Ciencias Médicas, Santiago de Cuba, Cuba.
Resumen
se presentan algunos elementos básicos sobre el uso y abuso de las pruebas de Ji al cuadrado de independencia y de homogeneidad en los informes finales de tesis de grado; así como la importancia del control del sesgo de confusión, la necesidad de tenerlo en cuenta en las investigaciones analíticas y algunos métodos para lograrlo.
Palabras clave: prueba de hipótesis, Ji al cuadrado, sesgo, tesis de grado.
ABSTRACT
Some basic elements on the use and misuse of independence and homogeneity chi-square tests in the final reports of theses are shown, as well as the importance of the confounding bias control, the need to take this into account in the analytic research and some methods to achieve it.
Key words: hypothesis testing, chi-square, bias, thesis.
INTRODUCCIÓN
La generalidad de los autores que efectúan investigaciones epidemiológicas, utilizan como recurso ilustrativo de sus resultados las tablas o cuadros estadísticos; para ello las formas más comunes de su presentación son las llamadas tablas de contingencia o de tabulación cruzada. Las mismas constan de dos dimensiones, las cuales a su vez contienen una variable, asimismo, cada variable se subdivide en dos o más categorías.
Las tablas de contingencia constituyen el asiento estructural de la prueba estadística, donde se pretende probar la hipótesis acerca de la asociación o relación entre 2 variables categóricas y a la que popularmente se le mal llama Prueba de Ji al cuadrado, cuando realmente se debe referir a la prueba de Ji al cuadrado de independencia o a la de homogeneidad, ya que existen múltiples test que se sustentan en esta distribución, entre las que figuran: las pruebas de Ji al cuadrado de bondad de ajuste, de tendencia lineal, de Mantel y Haenszel y hasta la prueba de Mc Nemar, la cual nos es más que un Ji al cuadrado modificado.1-3
En este artículo no se pretende exponer todas las particularidades de dichos test, pero sí resulta oportuno señalar algunos de sus fundamentos, de manera tal que permitan al investigador la selección correcta de uno u otro.
Ambas pruebas se inscriben dentro de los llamados métodos no paramétricos, que son aquellos cuyo modelo no especifica condiciones sobre los parámetros de la población de donde se extrajo la muestra; es decir, el modelo no implica el uso de hipótesis que prefijen valor alguno de los parámetros poblacionales, sino que estas versan sobre características no numéricas, tales como: el tipo de distribución poblacional, la independencia, entre otras.2,3
Resulta extremadamente llamativo, que las pruebas de independencia y homogeneidad son empleadas, en la gran mayoría de las situaciones prácticas, como una sola; en tal sentido es importante tener en cuenta, que si bien ambas pruebas son similares en cuanto a su procedimiento de cálculo, difieren teóricamente en más de un elemento, entre los que figuran:
- Número de muestras (no el tamaño de muestra)
- Hipótesis que se somete a prueba.
- Interpretación de los resultados en cada una de ellas
Se debe suponer en principio, que se selecciona una muestra aleatoria de tamaño N, de una población dada. Luego, los elementos de dicha muestra pueden ser clasificados de manera simple mediante el empleo de una escala asociada a una variable previamente seleccionada; esta escala debe ser exhaustiva y excluyente, o en forma múltiple si se utilizan 2 o más escalas correspondientes a variables dadas, alternativa esta última que origina las llamadas tablas de contingencia múltiples.
Para ilustrar lo expuesto anteriormente se muestra tabla 1
El ejemplo anterior muestra una tabla de contingencia de dos por dos (2x2), o sea 2 filas y 2 columnas, ya que ambas variables son dicotómicas, lo cual significa que cada una de ellas solo puede asumir 2 categorías. En la misma, el único resultado conocido de antemano es el de 400 (tamaño de la muestra), el resto de los valores, bien sea de las celdas (100, 70, 30, 200) o los referidos a los totales marginales (130, 270, 170, 230) son impredecibles antes de llevar a cabo la clasificación, debido esto al carácter aleatorio de lo observado en dicha tabla, con respecto a la muestra.
Esta particularidad hace que la prueba apropiada para validar los resultados sea la de Ji al cuadrado de independencia, en la cual siempre se trabaja con una sola muestra, muy útil además en la identificación de asociaciones (no causales) en los estudios transversales, también conocidos como estudios de prevalencia, siempre que las variables que aparezcan en la tabla sean categóricas.
Para exponer otra forma de obtener tablas de contingencia y su uso en relación con la prueba de hipótesis de homogeneidad, se utilizan los mismos datos de la anterior, solo que expresados a través de una ligera transformación en el modo de llevar a cabo el muestreo, el cual da origen a la información que aparece en la tabla. De la misma manera, si los investigadores quisieran estudiar si la condición respecto al cáncer de pulmón tiene el mismo patrón de comportamiento relacionado con el hábito de fumar, se seleccionan dos muestras aleatorias e independientes de individuos fumadores y no fumadores de tamaños 170 y 230 respectivamente; luego ambas se clasifican según hayan desarrollado o no el cáncer de pulmón y se obtiene la tabla 2
Muestras independientes (2) respecto al hábito de fumar de tamaños 170 y 230, clasificadas según presencia o no del cáncer de pulmón.
¿En qué difieren los resultados expuestos en las tablas 1 y 2? Se diferencian en que en la 2 ya se conocen previamente dichos resultados referidos a la última columna (170, 230, 400), los cuales no son consecuencia de la clasificación, a diferencia del resto de los valores. Esta es una particularidad que sugiere al investigador el empleo de la prueba de Ji al cuadrado de homogeneidad, por lo que la misma puede ser seleccionada en los estudios analíticos, siempre que las variables estudiadas sean categóricas.
La hipótesis que se somete a prueba en el mal llamado test de Ji al cuadrado de independencia es precisamente la independencia entre las variables, o lo que es lo mismo, la no existencia de asociación entre las variables en estudio. Esta se diferencia de la prueba de homogeneidad, donde la hipótesis que se somete a prueba es aquella en la cual no difiere la distribución de la variable estudiada en las N poblaciones, de donde se extrajo la muestra;2 por lo tanto, en el momento de interpretar los resultados obtenidos, resulta obvio que ambas pruebas conducen a conclusiones diferentes.
No obstante todo lo anteriormente expuesto, se considera oportuno señalar, que ambos test deben utilizarse preferentemente cuando las variables sean cualitativas nominales dicotómicas o politómicas; desafortunadamente es muy común utilizarlas cuando dicha variable es clasificada en una escala ordinal y exponer los resultados de la manera que sigue: a medida que se incrementa el efecto de la variable x, la variable y sufre cambios, lo cual es desde todo punto de vista incorrecto, ya que dichas pruebas son insensibles a los efectos de orden, por lo que en esos casos se deben utilizar otras pruebas de hipótesis. Estas se fundamentan en el grado de concordancia entre las frecuencias observadas y esperadas que aparecen en la tabla, las cuales al no ser visibles en la misma, deberían ser calculadas por el investigador mediante el producto de los totales marginales que se asocia a cada una de las celdas entre el gran total, aunque la gran mayoría de los programas estadísticos utilizados hoy día muestran información referida al comportamiento de estas frecuencias. 1-4
La principal causa del uso inadecuado de estos test, en un elevado porcentaje de las ocasiones en que se emplean, es que no tienen en cuenta el comportamiento de las frecuencias esperadas; por esta razón, es de suma importancia conocer que si más de 20 % de las celdas en una tabla de contingencia tienen frecuencias esperadas menores que 5, o una celda tiene un valor esperado menor que 1, ninguna de las 2 pruebas antes señaladas sería válida y por lo tanto esto obligaría al investigador a buscar alternativas. Así por ejemplo, si la tabla es de 2x2, la prueba de las probabilidades exactas de Fischer podría ser una solución. En el caso de que se trate de variables politómicas, el investigador deberá decidir si prefiere perder información, de manera tal que reagrupe sus datos para poder aplicar o no la prueba.
También es común observar el empleo de dichos test en muestras muy pequeñas, los cuales no deben ser utilizados en muestras inferiores a 20.
Algunos autores se refieren en los datos obtenidos a la magnitud o fuerza de la asociación de sus resultados, mediante el empleo de estas pruebas solamente.3-7 Es válido recordar que ellas solo permiten conocer de la existencia o no de asociación, ya que para medir la intensidad o fuerza de la misma se requiere de medidas como el riesgo relativo o su estimación y en el caso de los estudios de casos y controles, el Odds Ratio.
Entre los profesionales de la salud existe, en sentido general, una tendencia marcada a crear escalas cualitativas a variables que por su naturaleza son cuantitativas, así por ejemplo, es común observar como el peso de los individuos suele ser clasificado en bajo peso, normopeso, sobrepeso y obesos. La talla es frecuente clasificarla en baja, normal y alta, e igual ocurre con otras variables cuantitativas; sin embargo, debe tenerse mucho cuidado al realizar este proceder, pues al efectuar una operación de ese tipo se pierde información y en no pocos casos se crean escalas cualitativas con la finalidad de poder aplicar una de las pruebas aquí señaladas, sin conocer la existencia de pruebas como la T de student (para la comparación de medias) o su similar no paramétrica U de Mann-Whitney, que permitirían, incluso de una forma mucho más eficiente, arribar a conclusiones adecuadas.
En este mismo orden y dirección se debe agregar, que un número importante de los autores se limita a la búsqueda de asociaciones entre variables, sin tener en cuenta la posible influencia que puede tener en los resultados la existencia de factores externos, que de no ser considerada, pudiera llevar a conclusiones equívocas.
Una parte importante de la etapa de interpretación de los resultados y de evaluación de los hallazgos es analizar críticamente la posibilidad de que eventuales factores pudieran invalidar metodológicamente los resultados.8-10
En términos generales, teniendo en cuenta los resultados obtenidos, el investigador debe estar en condiciones de evaluar si los mismos pueden ser originados por:
1. Simple azar
2. Ocurrencia de error sistemático
3. Asociaciones causales
1. Simple azar
Estadísticamente es posible conocer y controlar la probabilidad de ocurrencia de error en la investigación desde fases muy tempranas, lo que puede suceder en la etapa de muestreo. También, la revisión y análisis preliminar de la información permite verificar la magnitud real de error proveniente de los datos recogidos; pero, a pesar de que el error aleatorio es imposible de eliminar, el conocimiento de su cuantía permite emitir juicios al considerar su magnitud en la evaluación de los resultados de la investigación. En dependencia del problema en cuestión y el nivel de conocimientos imperantes, el investigador debe decidir cuál es el nivel máximo de error tolerable para, por ejemplo, implementar en una población, una medida preventiva o de control.2
2. Ocurrencia de error sistemático
La participación del sesgo de confusión en los resultados obtenidos en una investigación puede ser muchas veces interrumpida, por lo que debe realizarse una cuidadosa revisión y análisis de las características del diseño de la misma, en particular aquellos aspectos referidos a la medición de las principales variables independientes del estudio (variables de exposición y covariables). Además, es esencial minimizar la probabilidad de existencia de errores sistemáticos derivados de la aplicación de instrumentos de medición, mediante la optimización de las condiciones necesarias para aplicar dichos instrumentos, a partir de su evaluación previa y su control permanente, durante la fase de trabajo de terreno y recolección de la información.1
Un capítulo importante en la investigación epidemiológica corresponde al análisis de los resultados, teniendo en cuenta la participación de variables que pudieran ejercer algún efecto sobre la relación encontrada. Esto podría manifestarse a través de la distorsión del efecto observado en relación con el real, debido a la desigual distribución de una variable extraña en los grupos estudiados (efecto de confusión).
3. Asociaciones causales
En el análisis de relaciones de causalidad, el investigador debe tener la certeza absoluta acerca de la direccionalidad de las asociaciones observadas (prospectiva o no) y considerar que la exposición estudiada pudiera corresponder realmente a un outcome o variable dependiente, al estudiar una cadena causal.3
• Variables confusoras
El efecto de confusión se produce, cuando en el análisis de una relación existe distorsión en el efecto estimado, el cual es provocado por la presencia de una variable extraña en el estudio de la asociación.11,12
La presencia de la variable extraña puede tener como efecto que el resultado sea diverso: en ocasiones determina la existencia de asociaciones positivas, las cuales en la práctica no son reales(error de tipo I o α ) o bien, pueden esconder asociaciones reales, las que en presencia de dicha variable extraña, quedan enmascaradas (error de tipo II o ß).
El concepto de confusión es crítico en el análisis epidemiológico y resulta más importante en el terreno de la investigación epidemiológica observacional o no experimental, que en el campo experimental. Esto se debe a que los estudios empíricos permiten un mejor control de este efecto por características inherentes a su tipo de diseño (la asignación aleatoria o el uso de matching o apareamiento de variables, en ambos casos durante el diseño de la investigación).3-6
Conceptualmente deben cumplirse algunos requisitos para considerar a una variable como potencialmente confusora:
- Esta variable debe estar simultáneamente asociada con la enfermedad (variable dependiente) en estudio y con la exposición,
- por lo tanto, debe ser un factor de riesgo para la afección estudiada,
- el factor extraño no debe ser un paso intermedio en la secuencia causal.
Todo lo anterior se corresponde gráficamente con la representación siguiente (figura 1).
Por ejemplo, en el análisis del efecto protector del Beta Caroteno, en relación con el cáncer del sistema digestivo, se encuentra evidencia favorable acerca del consumo de vegetales en la reducción del riesgo de cáncer, para concluir que el consumo de Beta Caroteno en la dieta rica en vegetales es una medida específica de protección contra el cáncer;11 sin embargo, en dicho ejemplo pueden existir al menos dos posibles variables confusoras a considerar. La primera es la edad, la cual se asocia con la incidencia de cáncer y con el nivel de consumo de verduras y hortalizas, lo cual podría verificarse si en el estudio se contara con información acerca de la constitución por edad de los sujetos estudiados.
Otra variable confusora podría ser el consumo de fibra en la dieta. En este caso, el nivel de consumo y tipo de fibra están relacionados de manera simultánea con las variables consumo de vegetales y cáncer, respectivamente. En ambos ejemplos se cumplen las condiciones previamente señaladas para poder considerarlas como tales. Si en el análisis no se tiene en cuenta la presencia de ellas, pudiera concluirse una recomendación errónea basada en una relación espúrea o ficticia.
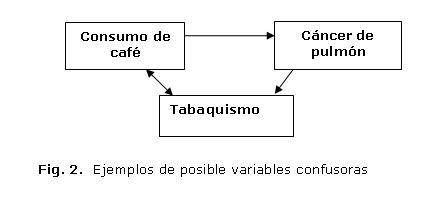
Para mayor claridad respecto a las características de las variables confusoras se plantearán tres situaciones hipotéticas (figura 2).
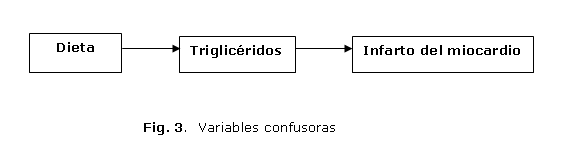
1. En este caso, el tabaquismo se relaciona simultáneamente con la exposición y con el desenlace. Corresponde realmente a una variable confusora. (figura 3).
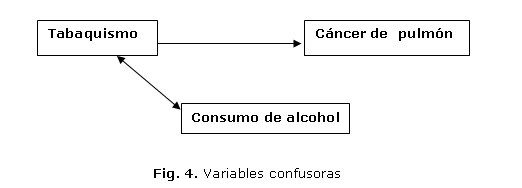
2. En la situación anterior, el nivel de colesterol sérico corresponde a una variable "intermedia", cabe destacar, que en la cadena causal precede al daño y es consecuencia de la exposición principal en estudio. En este caso no corresponde a una variable confusora (figura 4).
3. Finalmente, se da el caso en que la variable de exposición (tabaquismo) está asociada con una tercera (consumo de alcohol); sin embargo, esta última, no corresponde a una variable confusora, puesto que solo se asocia con la exposición y no con el desenlace.3
Siempre no resulta fácil saber si se cumplen los requisitos para que una variable sea considerada confusora. Por ejemplo, ¿cómo saber si una variable es factor de riesgo para el desenlace estudiado, si se desconocen los antecedentes al respecto? Para tales efectos, es posible que en el análisis se pueda obtener información mediante la desagregación de los datos recogidos.
En un hipotético ejemplo de estudio de casos (enfermos) y controles (sanos) destinados a establecer la existencia de asociación entre la exposición al consumo de café y el riesgo de cáncer en el páncreas, se estudian 100 casos y 100 controles, con el siguiente resultado (tabla 3).
El valor de Odds ratio correspondiente es:
OR= 60 x 180 = 3,86
140 x 20
Con referencia a lo anterior se concluye que el consumo de café está asociado a un mayor riesgo para padecer cáncer de esófago.
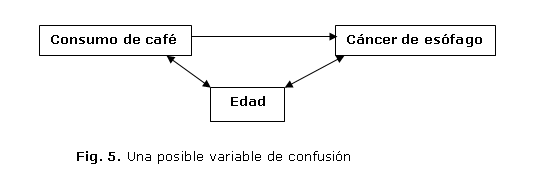
Una posible variable de confusión en este estudio pudiera ser la edad de los sujetos participantes en el mismo; si así fuera, primeramente se debería estudiar si la misma cumple con los requisitos para considerarla como tal. (figura 5 )
En primer lugar se analizará la relación existente entre las variables edad y cáncer de esófago (variable dependiente en estudio), para lo cual se utilizará toda la información desagregada acerca de la edad, considerada ésta dicotómicamente en menores o mayores de 40 años (tabla 4).
Como se observa, el porcentaje de pacientes con cáncer, mayores de 40 años es evidentemente superior (60 %) al de sujetos sanos (20 %).
Esto se puede validar mediante un test de Ji al cuadrado.
(X2 =65,01 p = 0,000)
En una segunda etapa, se estudiará la asociación entre las variables edad y "exposición" (tabla 5).
Se observa que la frecuencia de exposición no es uniforme en los estratos de edad, puesto que los mayores de 40 años tienen un mayor porcentaje de exposición. Evaluado esto mediante un test de Ji al cuadrado, se tiene X2 =49,23, p = 0,000
Finalmente, está claro que la edad de los sujetos, así categorizada, no es consecuencia del consumo de café, por lo cual se establece el cumplimiento de los requisitos para que la variable edad pueda considerarse como eventualmente confusora.
El control del sesgo de confusión es factible hacerlo en el diseño o en el análisis. Asimismo, en los estudios observacionales, que son los más frecuentes en Cuba, el método empleado por excelencia es el apareamiento.1 Al respecto, este es el proceso mediante el cual se selecciona a los controles (se tomó como ejemplo los estudios de casos y controles) teniendo en cuenta que estos tengan características similares a los casos con respecto a una o más posibles variables confusoras, tales como: sexo, edad y condición socioeconómica. Esta forma de reclutamiento de los controles tiene como ventajas, aumentar la eficiencia estadística y disminuir el sesgo asociado a factores de confusión conocidos.11
Entre las desventajas de parear en un estudio de casos y controles figuran: no poder analizar el posible efecto de riesgo de una variable de pareamiento, pues, por definición, son iguales para casos y controles; otra es el sobrepareamiento, consistente en una reducción de la eficiencia del estudio y se genera porque se parea por una variable, la cual es una condición intermedia en el camino causal entre exposición y enfermedad.3
No son pocos los que consideran el control de este sesgo en el análisis estadístico de los datos, pues existen varias alternativas para ello, pero la más empleada, por su utilidad para el control de más de un factor de confusión de una asociación básica, es la regresión logística multivariada.
REFERENCIAS BIBLIOGRÁFICAS
1. Lazcano Ponce E, Salazar Martínez E, Hernández Avila M. Estudios epidemiológicos de casos y controles. Fundamento teórico, variantes y aplicaciones. Salud pública Méx [Internet]. 2001[citado 25 Dic 2009];43(2). Disponible en: http://www.scielosp.org/scielo.php?script=sci_arttext&pid=S0036-36342001000200009
2. Piédrola Gil. Medicina Preventiva y Salud Pública. 11 ed. Barcelona: Masson; 2008.
3. Lam Díaz RM. Metodología para la confección de un proyecto de investigación [Internet]. [citado: 2 Sept 2009]. Disponible en: http://bvs.sld.cu/revistas/hih/vol21_2_05/hih07205.pdf
4. Cazau P. Guía de metodología de la investigación. La investigación descriptiva. [Internet]. [citado: 2 Sept 2009]. Disponible en:http://es.scribd.com/doc/6810391/Cazau-P
5. Ortiz Guerrero NA. La elaboración de los proyectos de investigación. [Internet]. [citado: 7 Sept 2009]. Disponible en: http://perso.wanadoo.es/noedroca/proyecto.pdf
6. Lanuez Bayolo MC, Martínez Llantada M, Pérez Fernández V. La hipótesis, preguntas científicas, idea rectora e ideas a defender. En: El maestro y la investigación educativa en el siglo XXI. [Internet]. [citado: 3 Jul 2010]. Disponible en: http://es.scribd.com/doc/55928029/12/La-hipotesis-preguntas-cientificas-idea-rectora-e-ideas-a-defender
7. El proyecto de investigación. [Internet]. [citado: 5 Sept 2009]. Disponible en: http://html.rincondelvago.com/proyecto-de-investigacion.html
8. Feal Cañizares P, Batista Moliner R. Metodología de la investigación en la APS. En: Álvarez Sintes R, Díaz Alonso G, Salas Mainegra I, Lemus Lago EM, Batista Moliner R, Álvarez Villanueva R, et al. Temas de medicina general integral. La Habana: Editorial Ciencias Médicas; 2001. p. 343-53.
9. Artile VL, Otero IJ, Osuma BI. Metodología de la investigación. [Internet]. La Habana: Editorial Ciencias Médicas; 2008 [citado 20 Ago 2009]. Disponible en: http://www.bvs.sld.cu/libros_texto/metodologia_dela_investigacion_leticia/completo.pdf
10. Salas M, Hofman A, Stricker BH. Confounding by indication: an example of variation in the use of epidemiologic terminology. Am J Epidemiol. 1999;149:981-3.
11. Grimes DA, Schulz KF. Bias and causal association in observational research. Lancet. 2002;359:248-52.
Recibido: 28 de febrero de 2012.
Aprobado: 6 de marzo de 2012.
Irlán Amaro Guerra. Universidad de Ciencias Médicas, avenida de las Américas, entre calles I y E, reparto Sueño, Santiago de Cuba, Cuba. Correo electrónico: irlan@medired.scu.sld.cu