ARTÍCULO ORIGINAL

 

 

Validez de las ecuaciones de estimación para la masa libre de grasa por el método de la impedancia bioeléctrica en cualquier población

 

Validity of the estimate equations for the fat free mass through the method of the bioelectric impedance in any population

 

 

Lic. Idelisa Bergues Cabrales,^I Lic. Maraelys Morales González,^I Dr. C. Luis Enrique Bergues Cabrales,^II Dr. Manuel Verdecia Jarque^III y Lic. José Pablo Martínez Tassé^I

^I Facultad de Ciencias Naturales y Exactas, Universidad de Oriente, Santiago de Cuba, Cuba.
^II Centro Nacional de Electromagnetismo Aplicado, Universidad de Oriente, Santiago de Cuba, Cuba.
^III Hospital Infantil Docente Sur "Dr. Antonio María Béguez César", Universidad de Ciencias Médicas, Santiago de Cuba, Cuba.

 

 

---

RESUMEN

Se efectuó un estudio para comparar entre sí 3 ecuaciones para la estimación de la masa libre de grasa --seleccionadas aleatoriamente de la bibliografía sobre el tema-- y estas, a su vez, con aquella estimada a partir del criterio clínico. Para esto se tuvieron en cuenta los valores no corregidos y corregidos de la resistencia eléctrica corporal, y se usaron como criterios estadísticos las diferencias de medias (distribución de la t de Student) y el método de Bland Altman. Los resultados mostraron que estas ecuaciones de estimación para la masa libre de grasa pueden usarse en la evaluación clínica (en sujetos aparentemente sanos y en enfermos) si a cada una le es introducido un factor de corrección.

Palabras clave: resistencia eléctrica, ecuaciones de estimación, masa libre de grasa, analizadores de bioimpedancia eléctrica.

---

ABSTRACT

A study with the purpose of comparing 3 equations --selected at ramdom from the literature on the topic-- for the estimation of fat free mass was carried out, and these, in turn, with that estimated when using the clinical approach. For this, the not corrected and corrected values of the corporal electric resistance were taken into account, and mean differences were used as statistical approaches (distribution of the Student´s t test) and the Bland Altman method. The results showed that these estimate equations for fat free mass can be used in the clinical evaluation (in apparently healthy persons and in sick individuals) if a correction factor is introduced to each of them.

Key words: electric resistance, estimate equations, fat free mass, analyzers of electric bioimpedance.

---

 

 

INTRODUCCIÓN

Lara Lafargue et al¹ demostraron que los analizadores BIA Bodystat^® 1500-MDD y BioScan^® 98 se pueden usar indistintamente para la caracterización bioeléctrica de sujetos aparentemente sanos y en enfermos (con diferentes afecciones) si son considerados sus respectivos factores de corrección para la resistencia eléctrica (R) y la reactancia capacitiva (Xc).

Aunque los valores de R no corregido (R_sc) y corregido (R_c), para cada analizador BIA, difirieron significativamente desde el punto de vista estadístico,¹ González Morales et al² demostraron que estos no condujeron a diferencias significativas en los valores del agua corporal total (ACT) y la masa libre de grasa (MLG) para las ecuaciones de estimación usadas, independientemente del tipo de población de estudio, el analizador BIA y la ecuación. Sin embargo, las 2 ecuaciones usadas para la estimación del ACT y las 2 para la estimación de la MLG difirieron significativamente. La estimación de la MLG es engorrosa en el orden clínico. Por esto, y a partir de los resultados notificados por González Morales et al,² surgió la interrogante de cuál de las ecuaciones de estimación sería la factible para las estimaciones del ACT y la MLG en sujetos aparentemente sanos y en enfermos (con determinada afección) pertenecientes a la población de Santiago de Cuba.

Para dar respuesta al planteamiento anterior, se diseñó esta investigación donde la variable de estudio fue la masa libre de grasa. El uso incorrecto de las ecuaciones de estimación para la MLG puede traer consigo que se sobrestime o subestime sus valores, lo que puede llevar a una interpretación incorrecta de esta variable, tanto en sujetos aparentemente sanos como en enfermos, en concordancia con lo informado por otros autores.^3-7

 

MÉTODOS

Se efectuó un estudio, como continuación del desarrollado por González Morales et al,² por lo que sus características generales, consideraciones éticas, analizadores de bioimpedancia eléctrica, sujetos aparentemente sanos e infanto-juveniles con diferentes enfermedades, procedimiento para la estimación de los parámetros bioeléctricos y confidencialidad de la información, fueron los mismos de estos autores, con el objetivo de conocer si las ecuaciones de estimación existentes en la bibliografía para la MLG, por el método BIA, son válidas en una población adulta aparentemente sana y en otra infanto-juvenil con diferentes afecciones. Los factores de corrección introducidos al Bodystat^® 1500-MDD fueron 3  Ω para R y + 9  Ω para Xc. Los mismos introducidos al BioScan^® 98 fueron de 14,7  Ω para R y 22  Ω para Xc. La frecuencia de trabajo fue 50 kHz.¹

En esta investigación se mantuvieron los 4 grupos experimentales: el primero estuvo formado por 31 adultos aparentemente sanos (14 hombres y 18 mujeres, entre 19 y 65 años de edad), denominado G1; el segundo se conformó por 31 pacientes infanto-juveniles con diferentes enfermedades (18 varones y 14 hembras, entre 3 y 15 años de edad), denominado G2, el cual, a su vez, fue dividido en 2 subgrupos: uno de 24 integrantes (G3), atendidos en el Servicio de Miscelánea del Hospital Infantil Docente Sur "Dr. Antonio María Béguez César", y el otro de 7 (G4), que padecían leucemia linfoblástica aguda y eran asistidos en el Servicio de Oncopediatría del mismo Hospital. Estos grupos, caracterizados por diferentes edades, tallas, sexos, pesos y colores de la piel, se conformaron ex profeso para evaluar, en condiciones de variabilidad extrema, cómo los valores de R_sc y R_c afectaron la MLG, y cómo este parámetro biológico estimado con diferentes ecuaciones difirió del calculado con el criterio clínico.

Este trabajo difirió del de González Morales et al ² en su concepción, tipos de ecuaciones de estimación para la MLG y en los criterios estadísticos usados, los cuales se exponen en los tópicos mencionados abajo.

• Ecuaciones de estimación para la masa libre de grasa

Los rangos de la MLG en la evaluación clínica para varones y hembras aparentemente sanos varían entre 80-85 y 70-75 % de su peso corporal, respectivamente.³ Los valores medios de la MLG, por sexo, denominada ecuación (0), se usaron como referencia para las ecuaciones de estimación de la MLG notificadas en la bibliografía médica. La ecuación (0) fue dada por:

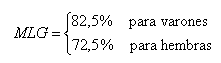
Las ecuaciones de estimación en la bibliografía para la MLG fueron las de Deurenberg, Lukaski y Van Loan, denominadas ecuaciones (1), (2) y (3), respectivamente, las cuales se escogieron al azar de todas las registradas (Lorenzo GS. Metabolismo de los pacientes con cáncer infanto-juvenil tratados con quimioterapia mediante la bioimpedancia eléctrica en 50 kHz [trabajo de diploma]. 2012. Departamento de Ingeniería Biomédica, Universidad de Oriente).

Donde T (en cm), P (en kg) y R (en  Ω ) fueron la talla, el peso y la resistencia eléctrica corporal del sujeto. Se establecieron 1 y 0 se para el sexo masculino y femenino, respectivamente (como lo referido por Lorenzo, mencionado previamente). La ecuación (0) se escogió como referencia para las ecuaciones (1), (2) y (3).

• Criterios estadísticos

Los resultados se expresaron como media y error estándar de la media. Este último parámetro se usó por la marcada heterogeneidad, ex profeso, de la muestra, en cada grupo experimental. Las diferencias estadísticas entre los valores de la MLG estimados a partir de los valores de R_sc y R_c, con ambos analizadores BIA, se evaluaron con las diferencias de medias de dos muestras (distribución de la t de Student), que se conocen sus medias, varianzas y tamaños, para un nivel de significación de 5 %. La diferencia no significativa entre las ecuaciones y los grupos correspondió cuando H₀ de la prueba de hipótesis se satisfizo (- t_tabulado ≤ t_calculado ≤ t_tabulado ); en caso contrario H₁ (hipótesis alternativa) se cumplió y, por ende, las diferencias fueron significativas. El análisis se efectuó con el paquete estadístico SPSS versión 11.5.1.

Las diferencias entre las ecuaciones (1), (2) y (3) y de cada una de estas con respecto a la ecuación (0) se calcularon, para los 2 analizadores BIA y los valores de R_sc y R_c, por medio de:

Los subíndicesi e j (i ≠ j) indicaron los pares de ecuaciones diferentes que se compararon. En el caso que las ecuaciones (1), (2) y (3) se cotejaron con la ecuación (0), el subíndice i se refirió a las 3 primeras ecuaciones, mientras el subíndice j, a la ecuación (0), por ser esta última la escogida como referencia.

El método de Bland Altman se usó para conocer si las ecuaciones (1), (2) y (3) podían sustituir a la ecuación (0), para 95 % de intervalo de confianza, porque la determinación de la MLG en la evaluación clínica es engorrosa, según Lorenzo.

 

RESULTADOS

La tabla 1 mostró los valores medios ± errores estándar de la media de la MLG estimada con las ecuaciones (0), (1), (2) y (3), para los valores de R_c obtenidos con el Bodystat^® 1500-MDD y BioScan^® 98, en G1, G2, G3 y G4. Se evidenció la no existencia de diferencias significativas entre las MLG estimadas con estos dos analizadores BIA, para cada grupo experimental y tipo de ecuación de estimación. Resultados similares se obtuvieron cuando fueron considerados los valores de R_sc (no mostrados).

Además se muestra que la MLG estimada con la ecuación (3) no difirió significativamente de las ecuaciones (0), (1) y (2) para todos los grupos experimentales y ambos analizadores BIA, excepto con aquella estimada con la ecuación (2), como se observó en el G2 para el BioScan^® 98. La MLG estimada con la ecuación (2) no difirió significativamente de la ecuación (0) (excepto en el G2, G3 y G4, para el BioScan^® 98) y de la ecuación (1) (excepto en el G2 y G3, para el BioScan^® 98). La MLG estimada con la ecuación (1) tampoco difirió significativamente de la ecuación (0) (excepto en el G1, para el Bodystat^® 1500-MDD y el BioScan^® 98).

Cuando se consideraron los valores de R_sc, la MLG estimada con la ecuación (3) difirió significativamente de la calculada con las ecuaciones (0), (1) y (2) para todos los grupos y ambos analizadores BIA. La MLG estimada con la ecuación (2) difirió significativamente de la calculada con la ecuación (0) (excepto en el G2 y G4, para el BioScan^® 98) y de la ecuación (1) (excepto en el G2, para el BioScan^® 98). Los valores de la MLG estimados con la ecuación (1) difirieron significativamente de aquellos calculados con la ecuación (0), con excepción del G1 (para ambos analizadores BIA) y el G2 (para el BioScan^® 98).

Aunque no se muestran los resultados, las variaciones a pares (∆MLG) entre las ecuaciones (0), (1), (2) y (3) revelaron que los valores de la MLG estimados con las ecuaciones (1), (2) y (3) fueron menores a la estimada con la ecuación (0), lo que fue más marcado para la ecuación (1). Sin embargo, estas tres ecuaciones sobrestimaron dichos valores respecto a los de la ecuación (0) para el G2, G3 y G4. Estos resultados fueron válidos para ambos analizadores y valores de R_sc y R_c. La comparación entre sí de las ecuaciones (1), (2) y (3) reveló que el error estándar de la media fue mayor que la media, en G1, G2, G3 y G4, excepto cuando las ecuaciones (1) y (2) fueron comparadas. Además, las variaciones a pares calculadas entre las ecuaciones (0), (1), (2) y (3) mostraron diferencias no significativas cuando los dos analizadores BIA se compararon, para ambos valores de R_sc y R_c.

En la tabla 2 se exhiben las bondades de ajuste (r²) y los factores de corrección (FC) que se obtuvieron por el método de Bland Altman. Para el G1, los FC fueron cercanos a cero para ambos analizadores BIA y los valores de R_sc y R_c. Sin embargo, los FC en el G2, G3 y G4 fueron mayores a los del G1, el menor fue para el G3 y el mayor para el G4. Existieron diferencias no significativas entre los FC cuando los dos analizadores BIA fueron comparados para R_sc y R_c.

 

DISCUSIÓN

Las diferencias significativas entre las MLG estimadas con las ecuaciones (1), (2) y (3) se debieron a sus dependencias con R, peso, talla, sexo y edad. Como la ecuación (3) contuvo a todas estas variables fue con la que mejor se estimó la MLG respecto a la de la ecuación (0). El hecho de que las MLG calculadas con estas tres ecuaciones de estimación difirieran de aquella estimada con la ecuación (0) puede explicarse en que el método BIA es doblemente indirecto.

El método del Bland Altman demostró que estas diferencias estadísticas no presentaban significación desde el punto de vista clínico, porque las MLG calculadas con las ecuaciones (1), (2) y (3) no difirieron de la estimada con la ecuación (0) cuando se consideraron sus respectivos FC. Los resultados de este método sugirieron que las ecuaciones (1), (2) y (3) pueden utilizarse indistintamente para la estimación de la MLG en sujetos aparentemente sanos (G1) porque los valores de FC fueron cercanos a cero. Sin embargo, para que estas tres ecuaciones sean usadas en sujetos enfermos con determinada afección hay que introducir el FC con su respectivo signo en cada una de ellas. Esto se explicó porque FC dependió del tipo de enfermedad y tipo de ecuación. El mayor valor de FC para G4 fue explicado por todas las alteraciones de la MLG, agua corporal total y masa grasa observada en los pacientes con leucemia linfoblástica aguda.

Para que la MLG estimada con la ecuación (1), (2) o (3) se aproxime a la calculada mediante la ecuación (0), hay que adicionar o restar una cierta cantidad de MLG (que coincide con el valor de FC) si el signo de FC es negativo o positivo, respectivamente. El factor de corrección debe ser considerado por los autores que usan las diferentes ecuaciones para la estimación de la MLG en sus poblaciones de estudio. Los resultados del actual trabajo no tienen precedente en publicaciones sobre el tema.

Una vía alternativa (larga y engorrosa) a la de esta investigación pudo ser el establecimiento de la ecuación para la estimación de la MLG en sujetos enfermos, por tipo de patología, sexo y edad, como se hizo en una población de sujetos aparentemente sanos en Santiago de Cuba,⁸ en concordancia con lo referido por Tong et al.⁹

Pudo concluirse que las ecuaciones de estimación para la masa libre de grasa pueden ser usadas en la práctica clínica, si sus respectivos factores de corrección son introducidos, teniendo en cuenta el sexo, el edad y el estado de salud del sujeto (aparentemente sano o enfermo), independientemente del tipo de analizador de bioimpedancia eléctrica usado y de si la resistencia eléctrica corporal fue corregida o no.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Lara Lafargue A, Bergues Cabrales LE, Verdecia Jarque M, Laurencio Martínez Y, Ortega Díaz Y. Parámetros bioeléctricos in vitro e in vivo, estimados con los analizadores Bodystat^® 1500-MDD y BioScan^® 98. MEDISAN. 2013 [citado 24 Jun 2016]; 17(9): 4054-63. Disponible en: http://bvs.sld.cu/revistas/san/vol17_9_13/san01179.htm

2. Morales González M, Verdecia Jarque M, Rubio González T, Bergues Cabrales LE, Lara Lafargue A, Martínez Tassé JP. Influencia de la resistencia eléctrica en la estimación del agua corporal total y la masa libre de grasa. MEDISAN. 2013 [citado 24 Jun 2016]; 17(10): 7001-10. Disponible en: http://bvs.sld.cu/revistas/san/vol17_10_13/san121710.htm

3. Harikumar R, Prabu R, Raghavan S. Electrical impedance tomography (EIT) and its medical applications: a review. Int J Soft Comp Eng. 2013; 3(4): 193-8.

4. Wolf GK, Gómez-Laberge C, Kheir JN, Zurakowski D, Walsh BK, Adler A, et al. Reversal of dependent lung collapse predicts response to lung recruitment in children with early acute lung injury. Pediatr Crit Care Med. 2012; 13(5): 509-15.

5. Lucas EG. Use of an electrical impedance tomography method to detect and track fractures in a gelatin medium [tesis]. Michigan: Michigan Technology University; 2014 [citado 24 Jun 2016]. Disponible en: http://digitalcommons.mtu.edu/cgi/viewcontent.cgi?article=1742&context=etds

6. Oh TI, Jeong WC, McEwan A, Park HM, Kim HJ, Kwon OI, et al. Feasibility of magnetic resonance electrical impedance tomography (MREIT) conductivity imaging to evaluate brain abscess lesion: in vivo canine model. J Mag Reson Imaging. 2013; 38(1): 189-97.

7. Grimnes S, Martinsen OG. Bioimpedance and Bioelectricity Basics. 2 ed. Oxford: Academic Press; 2008.

8. Nescolarde L, Núñez A, Bogónez-Franco P, Lara A, Vaillant G, Morales R, et al. Reference values of the bioimpedance vector components in a Caribbean population. Clin Nutr ESPEN. 2013; 8(4): 141-4.

9. Tong IO, Hyung JK, Woo CJ, Hun W, Oh IK, Eung JW. Conductivity image enhancement in MREIT using adaptively weighted spatial averaging filter. BioMed Eng OnLine. 2014 [citado 24 Jun 2016]; 13: 87. Disponible en: https://biomedical-engineering-online.biomedcentral.com/articles/10.1186/1475-925X-13-87

 

 

Recibido: 3 de septiembre de 2016.
Aprobado: 20 de noviembre de 2016.

 

 

Idelisa Bergues Cabrales. Facultad de Ciencias Naturales y Exactas, Universidad de Oriente, calle Patricio Lumumba s/n, Santiago de Cuba, Cuba. Correo electrónico:[e-mail]