ARTÍCULOS ORIGINALES

Dinámica probabilista temporal de la epidemia de dengue en Colombia

Temporary probabilistic dynamics of the dengue's epidemic in Colombia

Javier Rodríguez Velásquez,^I Sarith Vitery Erazo,^II Germán Puerta,^II Diana Muñoz,^III Ingrid Rojas,^II Laura Pinilla Bonilla,^IV Jessica Mora,^II Diego Salamanca,^II Natalia Perdomo^II

^I MD Profesor línea de profundización física y matemáticas aplicadas a la medicina. Universidad Militar Nueva Granada. Bogotá, Colombia.
^II Estudiante de Medicina y línea de profundización física y matemáticas aplicadas a la medicina, Universidad Militar Nueva Granada. Bogotá, Colombia.
^III Estudiante de Medicina e Internado especial física y matemáticas aplicadas a la medicina. Universidad Militar Nueva Granada. Bogotá, Colombia.
^IV MD. Universidad Militar Nueva Granada. Bogotá, Colombia.

 

---

RESUMEN

En el estudio de las enfermedades epidémicas se han aplicado diferentes modelos, tanto matemáticos como epidemiológicos, orientados hacia la comprensión y predicción de la dinámica de estos fenómenos. Dichas aproximaciones se fundamentan en la búsqueda de relaciones causales, tales como el clima, la precipitación pluvial, los movimientos poblacionales, entre otros, lo cual dificulta la generalización de dichas predicciones.
Partiendo de la construcción de dos espacios de probabilidad que cuantifican el número anual de infectados de dengue en Colombia en rangos de 5 000 y 10 000 infectados y del comportamiento probabilista de casos durante rangos de años consecutivos, se realizó una predicción temporal del número de casos de dengue en Colombia.El número de casos de dengue predicho para el 2007 se encontró en el rango de 35 000-45 000 y de 37 500-42 500, valores calculados con los rangos de 10 000 y 5 000 respectivamente. Estos valores fueron corroborados con los datos del Instituto Nacional de Salud que corresponde, en la semana epidemiológica 52, a 43 564 casos en Colombia, lo que evidenció una autoorganización matemática de la dinámica de aparición de casos de la epidemia de dengue de carácter predictivo. El estudio de las probabilidades durante la dinámica de la epidemia permite predecir la cantidad de infectados para el 2007 con predicciones simples, directamente comprobables y aplicables, lo cual evita el problema causal de los modelos matemáticos y establece predicciones más fáciles que economizan tiempo y recursos.

Palabras clave: Caminata al azar probabilista, probabilidad, epidemia, dengue.

---

ABSTRACT

Studying some epidemical diseases have been applied different models also mathematical like epidemiological, towards understand and predict the dynamical of this phenomena. These methodologies are founded in search for acausal relations, like climate, pluvial precipitation, demographic movements and more, which difficult to generalize these predictions. Starting from the construction of two sample spaces for probability, which quantify the annual infected number of dengue in Colombia in ranges of 5.000 and 10.000 infected, and from the probabilistic behaviour along consecutive group of years, it was made a temporal prediction about cases number of dengue in Colombia. The prediction for infected people for 2007 year was founded in the ranges 35000-45000 and 37500-42500, values calculated with the ranges of 10000 and 5000 respectively. These values ware corroborated with the National Health Institute data, for the accumulate value in the epidemiological week number 52, equals to 43564 cases in Colombia, it was evident a mathematical self-organization for the dynamics of infected people for dengue epidemics of predictive way. To study the probabilities along the epidemic dynamics led to predict the infected people for 2007, in a simple way, directly probed and useful, avoiding the causal problem for some mathematical models and establishing predictions in a more easy way, economizing sources and time.

Key words: Walking probabilistic, probability, epidemic, dengue.

---

INTRODUCCIÓN

La fiebre del dengue es una enfermedad infecciosa que se transmite al hombre a través del vector Aedes aegyptiy. La fiebre del dengue en su forma clásica se caracteriza por cefalea, osteomialgias, rash, y leucopenia, mientras que la variante del dengue hemorrágico se caracteriza por cuatro manifestaciones clínicas mayores. La variante clásica es la más frecuente, y con menos incidencia se observan casos de dengue hemorrágico.¹ La prevalencia mundial de dengue ha aumentado de forma dramática en las últimas décadas. Actualmente se considera una enfermedad endémica en más de 100 países de África, en el Este Mediterráneo, en el sureste de Asia y en el Oeste del Pacífico. Cerca de 2 500 millones de personas tienen riesgo de contraer esta enfermedad. Hacia el año 2002 la Organización Mundial de la Salud calculó que alrededor de 50 millones de casos de dengue ocurrían anualmente en el mundo.²

Cepas de dengue clásico y dengue hemorrágico se comenzaron a reportar a partir del año 1981 en las Américas. En los últimos 20 años se registró un aumento de 492 820 casos, de los cuales 77 000 correspondían a dengue hemorrágico.³ En la semana epidemiológica 39 del año 2007 el número de casos de dengue en las Américas era de aproximadamente 630 356 infectados.⁴ En la década de los 70 se reportaron por vez primera casos de dengue en Colombia. En el país el número de casos ha aumentado en los últimos 10 años, y para la semana epidemiológica 50 de 2007 se reportaron 41 773 casos por la Organización Panamericana de la Salud.^3,4

La aplicación de leyes y teorías físicas y matemáticas a diferentes sistemas ha permitido desarrollar medidas objetivas que facilitan una comprensión y predicción de la evolución de su dinámica; por ejemplo, se ha aplicado la teoría de la probabilidad al estudio de la monitoria fetal,⁵ y de la dinámica cardíaca en adultos,⁶ así como también, a través de la geometría fractal, se han estudiado diferentes estructuras anatómicas corporales que han permitido su caracterización matemática objetiva.^7-9 Previamente, Rodríguez y otros han trabajado en el desarrollo de una metodología que estudia la dinámica de diferentes epidemias, como la de malaria, dengue y VIH/SIDA, a través de la cual se establecieron predicciones del número de casos sin tener en cuenta las causas, basado en la Teoría de la Probabilidad y en la Caminata al Azar probabilista,^10,11 así como una predicción de los brotes de malaria en todos los municipios de Colombia por semana epidemiológica.¹²

La probabilidad es una medida matemática predictiva que cuantifica la posibilidad de la ocurrencia de un evento. La cuantificación de la totalidad de un número finito de eventos en el contexto de un experimento se realiza a través de la construcción de un espacio muestral, llamado también espacio de la probabilidad.^13-16 La frecuencia relativa de un evento particular es el cociente entre la cantidad de veces que se presenta tal resultado y el total de repeticiones del experimento. La frecuencia relativa en el lanzamiento de un dado para cada cara tiende a 1/6, que es justamente la medida de la probabilidad.¹⁴

La desviación media cuadrática es una medida de la mecánica de una caminata al azar probabilista que puede ser, por ejemplo, la representación de los consecutivos lanzamientos de una moneda en el contexto de un experimento. Por medio de esta se puede determinar si los eventos de un espacio de probabilidad son equiprobables o no, es decir, si la probabilidad está cargada para determinados eventos del espacio de probabilidad al comparar la desviación con su valor esperado. En el caso del lanzamiento de una moneda, cara y sello corresponden a los dos eventos probables.¹⁴

Como en las diferentes epidemias, el dengue también presenta un comportamiento irregular, que se ha calificado como impredecible y complejo, por lo cual es utilizada la teoría de la probabilidad y la desviación media cuadrática para cuantificar el comportamiento de la epidemia en el tiempo, lo cual caracteriza este fenómeno y establece predicciones probabilistas del número de infectados anuales.

MÉTODOS

DEFINICIONES

Probabilidad de casos infectados: La probabilidad del número de casos de dengue reportados en un año se define como el número de casos para dicho año dividido entre el total de casos:

Desviación media cuadrática del número de casos: Para estudiar si los valores del número de casos son equiprobables o no, es decir, si hay un cargamento de la probabilidad para eventos específicos del espacio muestral, usamos la fórmula de la desviación equiprobable de la caminata al azar:¹⁴

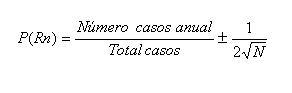
Donde N es el número de eventos del espacio muestral, es decir, el total de casos.

Definición de rangos

Sobre la base de la teoría de la probabilidad se evaluó el número de infectados anuales desde el año 1990 hasta 2006, a partir de la determinación de rangos de 5 000 y 10 000 casos, desde 0 hasta el máximo encontrado en los reportes de vigilancia epidemiológica del Instituto Nacional de Salud (INS), donde se definieron dos espacios de probabilidad: uno para tipo de rango, en el que cada espacio de probabilidad cuantifica la posibilidad de que en un año específico se registre un valor total para el número de infectados de dengue en Colombia que se encuentre contenido en los rangos establecidos, y en el que cada rango es considerado como un posible evento dentro de este espacio. De acuerdo con la variación anual del número de infectados para los últimos años con respecto al año de predicción, se determinó la amplitud del rango, teniendo en cuenta que las variaciones en los rangos son de aproximadamente 10 000 infectados y la precisión de la predicción puede ser mayor con los rangos de 5 000.

Cálculo de probabilidades y desviación media cuadrática

Posteriormente, se determinaron espacios de probabilidad cuantificando conjuntos de rangos de 10 000 agrupados de a tres, y conjuntos de rangos de 5 000 agrupados de a seis, en orden ascendente, calculando la probabilidad para cada rango respecto al conjunto total, y posteriormente la desviación media cuadrática para cada rango y las restas entre el valor de la probabilidad y su desviación media cuadrática. Finalmente, se compararon las restas entre los espacios de probabilidad construidos y se definió la existencia o no de un cargamento para aparición de los rangos en el tiempo.

Cálculo de la predicción

Finalmente, fue realizado un promedio aritmético de los valores que representan los rangos correspondientes a los últimos dos años y fue establecido el número de infectados a los que este valor correspondía a partir de una regla de tres, que resultó la predicción del rango de número de infectados para el año 2007. Posteriormente, se comparó el promedio del rango de la predicción con el valor real y se calculó el porcentaje de exactitud.

RESULTADOS

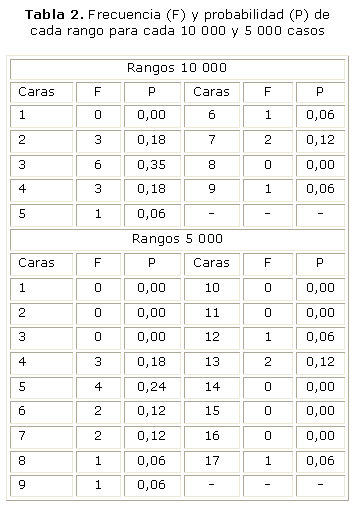
Dentro de los rangos establecidos de 10 000, el rango mínimo que contiene el mínimo valor de los infectados anuales en el período de 1990-2006, se encontró dentro del rango 1 con un valor de número de infectados correspondiente entre 0 y 10 000, y el valor máximo de infectados se encontró dentro del rango 9, que corresponde al valor de infectados entre 80 000 y 90 000. Mientras que con los rangos establecidos de 5 000, el valor mínimo de infectados se encuentra dentro del rango 4, que corresponde a un valor de infectados entre 15 000 y 20 000, y el máximo valor de infectados se encontró dentro del rango 17, que corresponde a un valor de infectados entre 80 000 y 85 000 (tabla 1).

FRECUENCIA Y PROBABILIDAD DE LOS RANGOS

De acuerdo con los rangos determinados de 5 000 y 10 000, se encontraron 17 y 9 rangos respectivamente dentro del período de 1990 y 2006. Los rangos fueron numerados de tal modo que el primero correspondiera al número de infectados entre 0 y 5 000 y entre 0 y 10 000, respectivamente. Los valores de probabilidad de los rangos de 5 000 se encontraron entre 0 y 0,24 y para los rangos de 10 000 entre 0 y 0,35 (tabla 2).

VALOR DE PROBABILIDAD Y DESVIACIÓN MEDIA CUADRÁTICA DE LOS CONJUNTOS DE RANGOS

Los valores de probabilidad para los conjuntos de grupos de 3 rangos se encontraron entre 0 y 0,667, cuyos valores correspondientes de desviación media cuadrática se encontraron entre -0,289 y 0,955, donde se halló un valor de diferencia entre estos últimos y el valor de probabilidad (valor esperado) entre -0,289 y 0,289 (los datos no se muestran). Los valores de probabilidad para los conjuntos de grupos de 6 rangos se encontraron entre 0,667, cuyos valores correspondientes de desviación media cuadrática se encontraron entre -0,288 y 0,955, donde se halló un valor de diferencia entre estos últimos y el valor de probabilidad (valor esperado) entre -0,288 0,288. Los rangos asociados a los valores del número de infectados correspondientes a los dos últimos años para los rangos de 5 000 infectados se encontró en el conjuntos de rangos 5-10, mientras que para los rangos de 10 000 infectados se encontró en el conjuntos de rangos 3-5 (tabla 3).

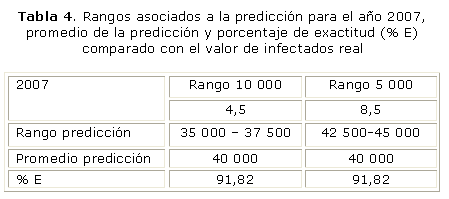
PREDICCIÓN TEÓRICA

Se encontró que los años 2005 y 2006 se hallaron en los rangos 8 y 9 respectivamente para los rangos de 5 000 y se hallaron en los rangos 5 y 4 respectivamente para los rangos de 10 000. El promedio aritmético de estos valores dio como resultado que el rango para el año 2007 para los rangos de 5 000 se encuentra entre 37 500 y 42 500, y para los rangos de 10 000 se encuentra entre 35 000 y 45 000 (tabla 4).

DISCUSIÓN

Este es el primer trabajo en el que, basado en cargamento de las probabilidades para cada año, se realiza una predicción del número anual de infectados de dengue en Colombia. Evaluar el cargamento de la probabilidad en el tiempo como un sistema dinámico reveló una autoorganización de la dinámica aplicable a la salud pública, que simplifica la toma de decisiones. Esta metodología se basa en el cargamento de las probabilidades en rangos de tiempo, lo cual permite establecer la predicción teórica con el número de infectados reportados correspondiente a los últimos dos años de forma simple y precisa.

La gran mayoría de trabajos científicos en el área de las epidemias están orientados específicamente al estudio de las relaciones causales del fenómeno de las epidemias.^17,18 Algunos modelos de predicción se basan en múltiples interacciones que consideran características de la dinámica de las epidemias, y otros se basan en el clima o condiciones de la población, con ciertas limitaciones, dado que su efectividad depende de las regiones y estaciones del año.^19,20 En trabajos realizados previamente se estudió la dinámica del número de casos de malaria y de dengue por año, cuya metodología se encuentra basada en la caminata al azar probabilista y la teoría de la probabilidad, y se analizó el comportamiento probabilista de las epidemias, mientras se realizó una predicción temporal de los casos, y se predijo el número de infectados para el año 2007.^10,11 En un estudio se predijeron, en rangos de semanas epidemiológicas, las condiciones matemáticas que se deben cumplir para un brote de la epidemia de dengue para todos los municipios de Colombia que reportaron al menos un caso de esta enfermedad, aplicables a la vigilancia epidemiológica como un sistema de alerta temprana.¹²

Este trabajo postula el determinismo probabilista para la dinámica de la epidemia de dengue en donde hay una coexistencia, tanto del determinismo como del probabilismo, para lograr predicciones de rangos probabilistas acertados de la dinámica. Al contrario, para la física clásica el determinismo de la mecánica es el fundamento, y en cambio, para la mecánica quántica es el indeterminismo basado en la probabilidad. De la misma manera, el fundamento de la primera es la causalidad, mientras que para la segunda es la acausalidad. La metodología desarrollada en este trabajo permite evidenciar un orden subyacente a la dinámica de la epidemia, sin necesidad de establecer relaciones causales para lograr predicciones que sean útiles, simples y aplicables al área de la salud pública.

AGRADECIMIENTOS

Este proyecto es resultado del proyecto MED 736, financiado por el Fondo de Investigaciones de la Universidad Militar Nueva Granada. Agradecemos a la Universidad Militar Nueva Granada, especialmente a al Dra Martha Bahamón, Vicerrectora Académica, al Dr. José Ricardo Cure Hakim, Vicerrector de Investigaciones, al Dr. Juan Miguel Estrada, Decano de la Facultad de Medicina, al Dr. Henry Acuña, Jefe de la división de Investigación Científica, y a la Dra. Esperanza Fajardo, directora del Centro de Investigaciones de Medicina, por su apoyo a la Línea de Profundización e Internado Especial en Teorías Físicas y Matemáticas aplicadas a la Medicina.

REFERENCIAS BIBLIOGRÁFICAS

1. World Health Organization. Dengue haemorrhagic fever: diagnosis, treatment, prevention and control. Geneva: Chapter 1: General considerations. World Health Organization; 1997:1-11. Disponible en: http://www.who.org

2. World Health Organization. Dengue and dengue haemorrhagic fever. Fact sheet N°117 (consultado: 28 de abril de 2002). Disponible en: http://www.who.org

3. Ocazionez RE. Serotipo, patrón de infección y dengue hemorrágico en área endémica colombiana. Rev Sal Públ. 2007;9(2):262-74.

4. PAHO. EID Updates: emerging and reemerging infectious diseases, region of the Americas. Dengue in the Americas: 2007;4(8). Disponible en: http://www.paho.org

5. Rodríguez J, Carmona V, Avilán N, Hincapié P. Análisis de la monitoria fetal con la teoría de la probabilidad. Rev Col Obst Gin 2004;55:26778.

6. Rodríguez J, Prieto S, Avilán N, Correa C, Bernal P, Ortiz L, Ayala J. Nueva Metodología Física y Matemática de Evaluación del Holter. Rev Col Cardiol. 2008;15:50-4.

7. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias: un modelo experimental en reestenosis, armonía matemática intrínseca de la estructura arterial. Rev Col Cardiol. 2002;10:65-72.

8. Rodríguez J, Álvarez L, Mariño M, Avilán G, Prieto S, Casadiego E, et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Dinámica fractal de la ramificación coronaria. Rev Col Cardiol. 2004;11:18592.

9. Rodríguez J, Lemus J, Serrano J, Casadiego E, Correa C. Medidas fractales cardiotorácicas en radiografía de tórax. Rev Col Cardiol. 2005;12:12934.

10. Rodríguez J, Correa C. Predicción temporal de la epidemia de dengue en Colombia; dinámica probabilista de la epidemia. Rev sal públ. 2009;11(3):443-53.

11. Rodríguez J. Dinámica probabilista temporal de la epidemia de malaria en Colombia. Rev MED. 2009;17(2):214-21 (en prensa).

12. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Sal Públ. 2010 (en prensa).

13. Laplace Pierre. Ensayo filósofico sobre las probabilidades. Barcelona: Altaya. 1995.

14. Feynman RP, Leighton RB, Sands M. Probabilidad. En: Feynman RP, Leighton RB, Sands M. Física. Vol. 1. Wilmington: Addison-Wesley Iberoamericana, S.A. 1964. p. 6-16.

15. Mood A, Graybill F, Boes D. Introduction to the theory of statistics. Singapore Mc. Graw-Hill. 1974.

16. Blanco L. Probabilidad, notas de clase. Universidad Nacional de Colombia. Departamento de Matemáticas y Estadística: 1996.

17. McKenzie FE, Bossert WH. A target for intervention in Plasmodium falciparum infections. Am J Trop MedHyg. 1998;58:7637.

18. Macdonald G. The Epidemiology and Control of Malaria. Oxford University Press. London: U.K.;1957;201.

19. Briët O, Vounatsou P, Gunawardena DM, Galappaththy GNL, Amerasinghe PH. Models for short term malaria prediction in Sri Lanka. Malaria Journal. 2008;7:76.

20. Jones A, Uddenfeldt U, Morse AP, Hastings IM, Gagnon AS. Climate prediction of El Niño malaria epidemics in north-west Tanzania. Malaria Journal. 2007;6:162.

Recibido: 20 de junio de 2010.
Aprobado: 14 de octubre de 2010.

MD. Javier Rodríguez Velásquez. Universidad Militar Nueva Granada. Cra. 79b # 51-16 Sur, Interior 5, apartamento 102, Bogotá, Colombia. tel: [phone]. Correo electrónico: [e-mail]