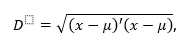Introducción
Aproximadamente existen 38,5 millones de personas que viven con el VIH a nivel mundial, ello conlleva la necesidad de estudiar el comportamiento de los linfocitos T CD4 en el tiempo, con la interacción de áreas como la estadística, matemáticas podemos generar un conocimiento más preciso que nos permita contribuir a la comunidad.
Para responder a ello se necesita definir métricas de distancia o similitud entre perfiles de expresión de cada conteo de linfocitos del paciente y usar esa métrica para encontrar agrupaciones de pacientes que sean más similares entre sí. Dada una métrica de distancia, se emplea una metodología para encontrar agrupaciones auto-similares. La agrupación es un procedimiento presente en cualquier campo que se ocupe de datos de alta dimensión, como lo es la información generada por biomarcadores dentro de un contexto clínico.
El comprender el comportamiento de los conglomerados a lo largo del tiempo, no sólo evaluarlo en el presente, nos proporciona las bases para futuras estimaciones numéricas, que generan ahorro al sistema de salud, así como un avance al área de la infectología.
Métodos
Estudio tipo cohorte retrospectiva, n= 142 observaciones de una cohorte de pacientes que vive con VIH, durante el periodo 2018-2022. A través de coordenadas de información se encontraron valores atípicos en las muestras o identificar grupos de muestras que necesitan más puntos de datos. El análisis es llevado a cabo en R(R Core Team 2022) y R Studio (Posit team 2023) para garantizar la reproducibilidad de resultados. Las tablas fueron producidas usando kableextra (Zhu 2021) y el reporte emplea knitr (Xie 2023) y rmarkdown (Allaire et al. 2023) para generarse. El flujo de trabajo utiliza la metodología del tidyverse (Wickham et al. 2019) para el manejo de datos, magrittr (Bache and Wickham 2022) para desarrollar líneas de fuga y la suite tidymodels (Kuhn and Wickham 2020) para presentar la modelación de manera integral.
Resultados
Visualización previa
Tabla 1 Recuento de linfocitos T CD4. Extracto de las primeras observaciones en donde podemos corroborar la estabilidad de los valores que traducen el buen estado inmunológico del paciente que vive con VIH a través del tiempo
| 2018 | 2019 | 2021 | 2022 |
|---|---|---|---|
| 525 | 738 | 708 | 766 |
| 338 | 344 | 403 | 411 |
| 648 | 736 | 522 | 555 |
| 462 | 256 | 701 | 792 |
| 52 | 8 | 55 | 74 |
Fuente: Base de datos del conteo de linfocitos T cd4 de personas que vive con VIH en Guerrero.
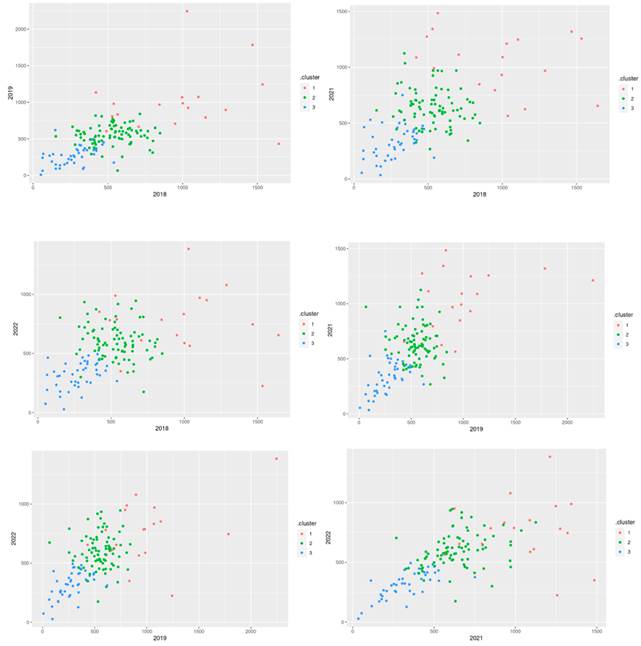
Una primera visualización (Figura 1A) se puede realizar con heatmaply (Galili et al. 2017) de la librería homónima que permite realizar agrupaciones tanto de variables como de observaciones.
 Fuente: Base de datos de conteo de linfocitos T cd4 de personas que viven con VIH.
Fuente: Base de datos de conteo de linfocitos T cd4 de personas que viven con VIH.Fig. 1 Mapa de calor para agrupaciones tanto de variables (dendograma superior) como de observaciones (dendograma en el lateral) y Matriz de distancias (estandarizadas).
Otra forma de ver las relaciones entre individuos es calcular su matriz de distancias, indicando el tipo de métrica. Se trabaja con la distancia de Euclidena para visualizar estas relaciones (Cuadro 1).
Cuadro 1 Distancia Euclideana para recuento de linfocitos T CD4. Extracto de la primera observación vs las siguientes diez observaciones
| Distancia: 1.7098398, 1.5035327, 2.4954613, 3.2225684, 3.6795326, 1.3228657, 1.7740600, 3.3759662, 1.7382425, 0.5694052. |
Fuente: Base de datos del conteo de linfocitos T cd4 de personas que viven con VIH en Guerrero.
La visualización de la matriz de distancias se puede llevar a cabo utilizando la librería factoextra (Kassambara and Mundt 2020) como lo muestra la Figura 1B.
Algoritmo k-medias
La implementación de la algorítmica no supervisada en esta sección sigue fuertemente el estilo de modelación en (Álvarez Liébana, n.d.) y (Amat Rodrigo, n.d.). Con esta base de datos se calculó la distancia euclidiana para encontrar el comportamiento de las observaciones a lo largo del tiempo y poder agrupar en conglomerados a través del algoritmo de k-medias. Este algoritmo busca agrupar las observaciones en k grupos de tal forma que cada conglomerado minimice la suma de cuadrados de las distancias de cada observación al centro del conglomerado.
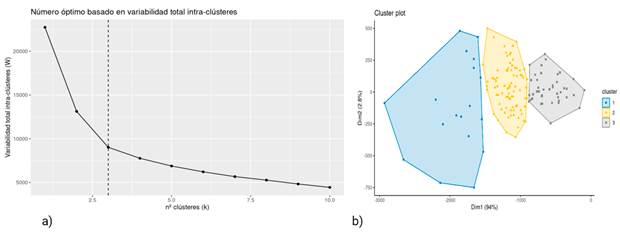
La fórmula para calcular la distancia de Euclidiana se define como:
Donde
D |
representa el valor calculado de la distancia |
x |
es el vector de observaciones |
es |
la media de las observaciones |
La métrica de distancia es simplemente una medida de cuán similares son las expresiones entre sí. Hay muchas opciones para las métricas de distancia y la elección de la métrica es bastante importante para la agrupación. Por ejemplo, se cuenta con observaciones de 142 pacientes de 2018 a 2022, y como se muestra en la Tabla 3, se desean encontrar similitudes en función de sus recuentos de T CD4 durante el periodo de estudio.
En la tabla 2 las columnas muestran los centroides, el tamaño, la suma de cuadrados y la etiqueta para cada clúster.
Tabla 2 Agrupación por k-medias
| 2018 | 2019 | 2021 | 2022 | Tamaño | Suma cuadrados | Etiqueta |
|---|---|---|---|---|---|---|
| 1.6311 | 1.6361 | 1.58954 | 1.0475 | 18 | 106.3564 | 1 |
| 0.0769 | 0.0789 | 0.1414 | 0.2862 | 82 | 105.7133 | 2 |
| -0.8493 | -0.8553 | -0.9574 | -1.0078 | 42 | 39.0635 | 3 |
Fuente: Base de datos del conteo de linfocitos T cd4 de personas que viven con VIH.
La Tabla 2 devuelve métricas del modelo. Una de ellas es la suma de cuadrados total dentro del conglomerado que se busca minimizar al realizar el conglomerado de k-medias. Para verificar la bondad de ajuste se toman en cuenta la suma de cuadrados dentro de cada conglomerado y entre los conglomerados, así como la suma de cuadrados totales.
En la tabla 3, las columnas muestran la suma de cuadrados totales, la suma de cuadrados totales dentro de cada clúster, la suma de cuadrados entre conglomerados y el número de iteraciones.
Tabla 3 Métricas del modelo de agrupación por k-medias
| Suma de cuadrados totales de la distancia Euclidiana | Suma de cuadrados dentro de cada clúster de la distancia Euclidiana | Suma de cuadrados entre conglomerados de la distancia Euclidiana | Iteraciones |
|---|---|---|---|
| 564 | 251.1333 | 312.8667 | 2 |
Fuente: Base de datos de conteo de linfocitos T cd4 de personas que viven con VIH.
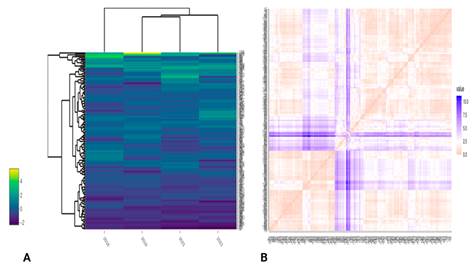
Se aplicó el algoritmo k-medias y se llevó a cabo la prueba del método de “codo” para encontrar el número óptimo de conglomerados.
Se encontró que este valor óptimo es de 3 agrupaciones en la población. En el Cuadro 1 se muestra la rutina en R para encontrar el número óptimo de conglomerados. Se hace la lectura de la base de datos, se filtra la columna de nombres de cada paciente, se calcula la distancia Euclidiana y se aplica el algoritmo de k-medias al objeto resultante por la distancia Euclidiana.
 Fuente: Base de datos de conteo de linfocitos T cd4 de personas que viven con VIH.
Fuente: Base de datos de conteo de linfocitos T cd4 de personas que viven con VIH.Fig. 2 a) Gráfica de codo para el método de k-medias. b) Nube de puntos de los conteos de linfocitos T CD4 a lo largo del tiempo agrupado por conglomerado proyectada en las dos primeras componentes principales que representan la mayor varianza en la nube de puntos de toda la base de datos.
En el Cuadro 2 se muestra la agrupación resultante por el algoritmo de k-medias. Se observa en la distribución de los conglomerados un predominio del conglomerado número 3. Este resultado puede apreciarse en la Tabla 3 con la distribución de frecuencias por conglomerado.
Cuadro 2 Resultado del agrupamiento por la distancia de Euclidiana y el algoritmo de k-medias
| [1] 2 3 2 2 3 2 2 2 2 2 2 2 3 2 3 2 1 2 2 2 2 2 2 2 2 2 2 3 3 2 2 3 3 1 3 2 2 2 2 3 2 [42] 2 1 2 2 3 3 3 2 1 3 1 2 2 3 2 2 3 2 2 1 2 3 1 2 2 3 3 3 2 2 2 1 2 2 3 2 1 2 2 3 2 [83] 3 2 3 3 2 3 2 2 1 3 3 1 3 1 2 3 2 2 2 2 3 2 2 2 2 3 1 3 2 2 1 1 2 3 2 1 2 2 3 2 2 [124] 3 3 2 2 2 1 3 2 3 2 3 2 3 3 1 2 2 2 2 |
Tabla 4 Tabla de frecuencias donde se observa la distribución del comportamiento de linfocitos T CD4 por conglomerados
| Conglomerado 1 | Conglomerado2 | Conglomerado 3 |
|---|---|---|
| 18 (azul) | 82 (amarillo) | 42 (morado) |
Fuente: Elaboración propia.
Tabla 5 Descripción de conglomerados: promedio de linfocitos T CD4 anuales por conglomerado
| Clúster | 2018 | 2019 | 2021 | 2022 |
|---|---|---|---|---|
| 1 | 961 | 1007.9444 | 1045.1667 | 767.1111 |
| 2 | 530.8049 | 551.2073 | 638.2805 | 599.5610 |
| 3 | 274.3810 | 277.1667 | 329.4762 | 314.7619 |
Fuente: Elaboración propia.
Conglomerado 1: Este conglomerado muestra caídas y ascensos abruptos en su recuento de linfocitos y su recuento promedio es el más alto de los tres conglomerados durante el periodo de estudio. Refleja un buen estado inmunológico.
Conglomerado 2: Este grupo es el más numeroso de los tres conglomerados con un recuento de linfocitos T CD4 promedio de 600. Este grupo logra detectar una caída leve durante el último periodo del estudio, sin embargo, también muestra una mejoría relativa en el comportamiento durante los demás años de estudio, refleja estabilidad del estado inmunológico en el tiempo.
Conglomerado 3: Este grupo muestra un comportamiento de mejoría en el recuento de linfocitos T CD4 a lo largo del periodo de estudio, pero arroja los valores promedio más bajos de los tres grupos, con un recuento alrededor de los 300 linfocitos T CD4. Lo que traduce mayor vigilancia médica por posibilidad de descender a cifras con mayor susceptibilidad de desarrollar tuberculosis, toxoplasmosis, etc.
Y se puede visualizar qué tan bien funcionó la agrupación en cada nube de datos de años dos a dos en la Figura 3.
Discusión
Durante la evolución del tiempo, y empleando k-medias se definieron 3 conglomerados, el ascenso en el conteo muestra mayor estabilidad en el conglomerado 2, valores más altos el 1 y bajos el 3. El análisis de los valores numéricos del conteo de linfocitos T CD4 a través de una serie de tiempo puede contribuir a generar un ahorro monetario al sistema de salud de México, pues hay evidencias de patrón matemático que traduce memoria.16,17 No encontramos investigaciones sobre la dinámica de linfocitos utilizando la distancia euclidiana, con la cual podríamos generar contraste. Consideramos estar arrojando bases que contribuyan a nivel nacional a generar alguna modificación en las guías respecto al intervalo entre las tomas de cuantificación de CD4, y con ello generar un ahorro al sistema de salud, e invertir en la prevención.
Conclusión
El comportamiento de linfocitos T CD4 mejora relativamente durante el periodo de estudio (2018-2022). También se encontró que el comportamiento promedio de linfocitos T CD4 a lo largo del estudio se estabilizó entre los grupos hacia un recuento sobre los 500 linfocitos. Sin embargo, existen observaciones escasas atípicas con cambios abruptos en el recuento de linfocitos T CD4, por lo que se sugiere dar seguimiento temporal al comportamiento de la dinámica de linfocitos T CD4 para pacientes que viven con VIH en Guerrero. Esto pudiera significarse un ahorro importante al sistema de salud.