INTRODUCCIÓN
Las técnicas estadísticas multivariadas son aquellas que analizan múltiples características, medidas en un mismo individuo. Constituyen una generalización de las técnicas univariadas y bivariadas, donde todas las variables deben ser aleatorias y estar interrelacionadas de tal forma que no tenga sentido interpretar de forma aislada sus diferentes efectos.1
Los modelos de análisis multivariado son empleados con más frecuencia en los estudios observacionales acerca de la etiología y el pronóstico de una enfermedad, y en ocasiones en los estudios de diagnóstico o de intervención.2
El análisis multivariado está presente en los estudios de causalidad, cuya estrategia debe partir de un buen diseño, donde se involucren como variable dependiente el desenlace y como covariables los supuestos factores causales, donde son importantes los posibles factores confusores que deben incluirse en el análisis y se toman precauciones para evitar posibles sesgos.3
En los estudios observacionales, donde no es posible hacer una asignación aleatoria de los individuos a los diferentes grupos de estudio, es muy útil el análisis multivariado, ya que permite el ajuste de las características basales de los grupos para lograr una aproximación estadística razonable a la estimación del efecto de la intervención, una mayor economía en el análisis de los datos, hacer predicciones, el control de las variables confusoras y obtener una mayor consistencia en la inferencia estadística.
Las técnicas multivariadas son herramientas que permiten al investigador extraer abundante información de los datos disponibles. Las mismas son complejas y requieren para su utilización de un conocimiento profundo de sus fundamentos. Los paquetes estadísticos han permitido una amplia aplicación de las mismas, aunque algunas veces por insuficiente conocimiento y respaldo teórico, su empleo no ha sido el adecuado.4) Para el investigador novel que no está familiarizado con los términos empleados en el texto se sugiere consultar el anexo de terminología de uso frecuente.
La presente investigación tiene como objetivo exponer las técnicas multivariadas empleadas en el estudio de la causalidad en las ciencias biomédicas según su finalidad y tipo de variables.
MÉTODOS
Para lograr el objetivo propuesto se realizó una investigación documental con la revisión de las bases de datos biomédicas y la literatura apropiada por su carácter científico y actualizado. Se identificaron las regularidades y diferencias que permitieron la organización y elaboración de un material resumen de estas técnicas, donde se incluye el análisis estadístico implicativo, empleado recientemente en las Ciencias Médicas.
se llevó a cabo una revisión de la literatura sobre el tema en bases de datos bibliográficas como Pubmed/Medline, SciELO, SCOPUS, Web of Science, EBSCOhost, Google, entre otras. Se emplearon en la estrategia de búsqueda como descriptores los consignados en las palabras claves del artículo, los mismos fueron utilizados en idiomas inglés, francés, portugués y español, combinados con los operadores lógicos. De los más de 200 documentos digitales encontrados, se escogieron los de mayor actualidad, elaborando un informe donde se agrupan las técnicas según su objetivo y tipos de variables empleadas en el análisis.
DESARROLLO
Para el estudio de la causalidad, al tener el paradigma multicausal que ha dominado desde el siglo anterior y la multicausalidad de los eventos en Medicina, las técnicas estadísticas apropiadas son las multivariadas, sobre todo las explicativas.
No obstante, en algunos casos se requiere de un primer análisis exploratorio, donde se hace necesario el empleo de las técnicas multivariadas descriptivas, para reducir dimensionalidad de los datos o agruparlos de manera conveniente; de ahí la utilidad de conocer todas las técnicas y en qué momento emplearlas.
Clasificación de las técnicas estadísticas multivariadas
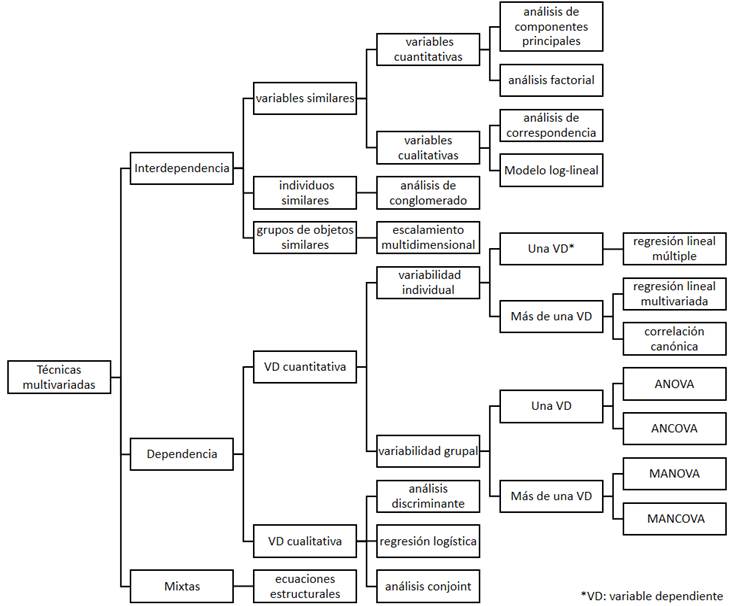
Para saber qué técnica se debe aplicar, es necesario conocer cómo están medidas las variables que se analizan en el estudio.4,5) También es preciso conocer el tipo de relación existente entre las variables. La dependencia o no entre variables se determina por el conocimiento a priori del investigador. Como consecuencia de estos aspectos, los principales métodos de análisis multivariado empleados en la inferencia causal, se pueden agrupar según su finalidad (Fig. 1) en:
Métodos descriptivos o de interdependencia: son empleados para verificar las relaciones de interdependencia y describir la estructura de los datos según se quieran identificar. Se dividen en:
variables similares
con variables cuantitativas se emplean el análisis de componentes principales y el análisis factorial exploratorio. Estas técnicas permiten reducir la dimensionalidad de los datos, con lo que se pueden descartar atributos irrelevantes para la toma de decisiones, que conspiran además en contra de la eficiencia de los algoritmos propios de las técnicas empleadas a posteriori. (5) Las nuevas características encontradas son combinación lineal de las anteriores y se les llama componente si se forman por variables observadas y factores si se forman por variables no observadas.
con variables cualitativas se emplean el análisis de correspondencia y el modelo log-lineal para tablas de contingencia con más de dos entradas.
individuos similares
con variables de cualquier tipo se emplean el análisis de conglomerado (cluster). Es una técnica de agrupamiento que clasifica las unidades de la matriz de datos en conglomerados (grupos internamente homogéneos y heterogéneos entre ellos) con el empleo de diferentes índices de similaridad o de distancia. Estas clasificaciones pueden ser jerárquicas (ascendente o descendente) en los que no se establece a priori el número de grupos, o no jerárquicas en las que se parte de un número dado de grupos según hipótesis o cálculos previos.5,6
grupos de objetos similares
se emplea el escalamiento multidimensional, técnica que permite la reducción de datos, al tratar que la distancia entre los objetos en el nuevo espacio dimensional reducido sea lo más parecida a las distancias del espacio original, tal como la construcción de un mapa a menor escala. (5
Métodos explicativos o de dependencia: son empleados para analizar las relaciones de dependencia que permiten explicar o predecir determinados eventos. Según el tipo de variables dependientes pueden ser:
con variable dependiente cuantitativa
para explicar la variabilidad individual se puede emplear la regresión lineal múltiple, en el caso de una sola variable dependiente, o la correlación canónica y la regresión lineal multivariada en el caso de más de una variable dependiente.
para explicar la variabilidad grupal (los grupos condicionan la variable categórica) se emplea el análisis de varianza o de covarianza (ANOVA o ANCOVA) si es una sola variable o un análisis multivariado de varianza o de covarianza (MANOVA o MANCOVA) si se trata de más de una variable dependiente. En el ANCOVA y MANCOVA las variables explicativas pueden ser medidas en cualquier escala. (6
con variable dependiente cualitativa:
el análisis discriminante para predecir si un individuo pertenece a un grupo cuando se cumple el supuesto de normalidad.
la regresión logística binaria para respuesta dicotómica o multinomial para respuesta politómica. (7
el análisis conjunto (conjoint), que es el único entre los métodos multivariados en el cual el investigador construye primero un conjunto real o hipotético de variables, al combinar niveles escogidos de cada atributo. (1) Según el número de atributos se emplean variantes del método como los modelos auto-explicados y los modelos adaptativos e híbridos.
Métodos mixtos o estructurales que combinan dependencia con interdependencia como las ecuaciones estructurales.
Las técnicas antes mencionadas pueden ser de amplio uso en la práctica, ya que en la clínica es frecuente emplear como variables, múltiples determinaciones de laboratorio como urea, creatinina, glucemia, colesterol, entre otras (variables cuantitativas) con la cual se pueden hacer investigaciones y análisis multivariados en dependencia de lo que se desea probar.
Por ejemplo, en un estudio donde se quiere evaluar la eficacia de cierto tratamiento para la Diabetes Mellitus se han medido un considerable número de variables que se corresponden con estas determinaciones del laboratorio clínico y se tiene interés en reducir su número. En este caso se puede emplear un análisis de componentes principales. (Método descriptivo o de interdependencia).
Si se quiere conocer si existen diferencia con respecto a estos parámetros del laboratorio entre varios grupos de individuos sometidos a diferentes dietas (factores que representan variables cualitativas), es posible emplear un MANOVA (Método explicativo o de dependencia).
Así, al analizar los tipos de variables y el objetivo que se quiere lograr, es posible identificar la técnica requerida en cada caso. No es tarea fácil decidir porque, en ocasiones, existe más de una técnica con la misma finalidad, por lo que es necesario conocer además qué pruebas son más robustas.
Al igual que existe evidencia de que las pruebas con una sola variable dependiente (regresión, ANOVA, ANCOVA, etc.) son robustas bajo la violación de los principios de normalidad y homocedasticidad (excepto cuando las muestras son muy pequeñas y desiguales); las técnicas multivariantes, con muestras grandes (n > 30) también son suficientemente robustas ante ligeras desviaciones de los supuestos estadísticos (excepto en algunas técnicas como los modelos de ecuaciones estructurales donde el tamaño muestral debe superior a las 100 unidades).4
Entre estos métodos multivariados, los más empleados para el estudio de la causalidad son la regresión múltiple y las ecuaciones estructurales.
Regresión múltiple
En los estudios observaciones, en los que no es posible asignar experimentalmente valores de una variable predictiva, al investigador le interesa conocer los efectos de múltiples variables predictivas sobre un resultado y para ello puede usar los modelos de regresión que sintetizan la información sobre variables predictivas individuales con el uso de todo el conjunto de datos. Los coeficientes estimados con el modelo son parámetros estadísticos descriptivos muy potentes que permiten obtener un significado de los datos.
Los métodos de regresión múltiple se emplean según el tipo de variable dependiente que se analiza, así se tienen, entre los más empleados:
Regresión lineal: cuando la variable dependiente es continua. Los cambios de la covariable (aumento o disminución) influyen en el valor esperado de la variable dependiente de una manera lineal. Cada coeficiente de regresión representa el cambio que se espera en la variable de resultado por cada unidad de cambio en la covariable.3
Regresión logística: cuando la variable dependiente es categórica. En su forma binaria es muy empleada en la identificación de factores de riesgo o pronósticos cuando la variable dependiente es dicotómica, por ejemplo, vivo o fallecido o enfermo o no enfermo, y se pretende encontrar la probabilidad de que ocurra el desenlace en estudio con la influencia o no de otras variables. También puede ser multinomial cuando permite tratar situaciones en las que la variable respuesta tienen más de dos de alternativas posibles, sean ordinales o no.7
Regresión de Cox (Modelo de riesgos proporcionales): empleada en los estudios de supervivencia, donde la variable dependiente está en función del tiempo transcurrido hasta un determinado evento y se quiere determinar simultáneamente el efecto de una serie de factores que pueden alterar dicho tiempo. Ese efecto se presenta como la razón de riesgo (HR de Hazard Ratio) y expresa la magnitud en la que una variable aumenta o disminuye el riesgo de ocurrencia de un desenlace en el tiempo, por lo que supera a la técnica bivariada de Kaplan Meier.8
Regresión binomial: empleada cuando la variable de respuesta es dicotómica, es decir, el resultado solo puede adoptar uno de dos valores posibles como enfermar o no enfermar, morir o sobrevivir. En estos casos modela el logaritmo de una proporción (p), que bien podría ser la incidencia o la prevalencia de una enfermedad.3
Regresión de Poisson: empleada cuando la variable dependiente se ajusta bien a una distribución de Poisson (distribución que representa la probabilidad de que un determinado número de eventos ocurra durante un periodo de tiempo en un espacio o población especificada), para cualquier combinación de valores de la covariable. Una variable Poisson se presentan como la tasa de un evento de interés, por ejemplo, el número de fallecidos por determinada causa en una población específica durante el periodo de observación. Esta técnica modeliza bien situaciones de conteo en una unidad de tiempo.9,10
Regresión discontinua: apropiada en diseños cuasi-experimentales pretest-postest en los que se investiga el efecto de las intervenciones asignadas por encima o por debajo de un valor de corte o umbral. Mediante la comparación de las observaciones en un entorno del valor umbral, es posible estimar el valor del efecto de tratamiento promedio en los casos que la aleatorización es imposible.11,12
Para hacer un uso correcto de los resultados de una regresión se debe conocer el papel que cumplen las covariables, su adecuada codificación e inclusión en el modelo seleccionado, los supuestos básicos de la regresión, así como los métodos para evaluar el ajuste del modelo y la interpretación de los resultados.
En general, en el caso de desenlaces continuos, se pueden generar modelos de regresión lineal múltiple o modelos más flexibles como los aditivos generalizados que transforman automáticamente las covariables que no tienen una relación lineal con el desenlace. En el caso de desenlaces dicotómicos, se generan modelos de regresión logística o extensiones como la regresión logística bayesiana naive, los modelos aditivos generalizados, las particiones recursivas de un árbol de regresión o de clasificación u otros modelos de inteligencia artificial como las redes neuronales y las máquinas de soporte vectorial. Para desenlaces en función del tiempo hasta el evento se usa el método de riesgos proporcionales de Cox o métodos paramétricos que modelan en relación con las distribuciones exponencial, Weibul o de Poisson, entre otras (8
Para validar estos modelos se puede dividir la muestra en varias partes en cada una de las cuales el modelo se vuelve a estimar y se comparan los resultados para lo cual se pueden emplear las técnicas de remuestreo, donde se determina que el modelo es válido si la predicción del desenlace es igual en los datos en que se desarrolló y en los datos nuevos.
Las técnicas de remuestreo como el jacknife o el bootstrap consisten en seleccionar n muestras (submuestras) a partir de una muestra inicial. Esa selección de muestras se hace con reemplazo, con el empleo de la simulación computacional. El método de remuestreo es una buena opción para realizar estimaciones cuando los estadísticos son difíciles de manipular algebraicamente. El método Jackknife es una aproximación lineal del bootstrap, útil para la varianza y el sesgo.13
Los problemas en la no validez de estos modelos pueden deberse a deficiencias en el diseño, sobreajuste a los datos de la cohorte inicial, deficiencias o diferencias en el sistema de salud, diferencias en los métodos de medición y en las características de los pacientes.8
Ecuaciones estructurales
Los modelos de ecuaciones estructurales surgen para flexibilizar los modelos de regresión, al ser menos restrictivos al incluir errores de medida en las variables dependientes e independientes. Matemáticamente, son más complejos de estimar y por ello su uso no se extendió hasta 1973, cuando apareció el programa LISREL;14 ya en 2007 se facilitó la estimación en entorno gráfico, a través del programa AMOS.15
Estos modelos comprenden una serie de procedimientos que permiten probar la relación entre variables observadas (medidas directamente) y latentes (constructos medidos a través de otras variables observadas).16,17
Cuando el modelo se compone solo de variables observadas, la técnica se conoce como análisis de ruta, de camino o de sendero (path analysis) y es similar al análisis de regresión lineal clásico con la ventaja de que es posible estimar el efecto indirecto y total que tiene una variable sobre otra.18
Cuando el modelo mezcla ambos tipos de variables se convierte en análisis de estructura de covarianza. Este análisis puede ser recursivo si admite una dependencia unidireccional o no recursivo si se da una relación recíproca entre dos variables.1) Además puede ser un análisis factorial confirmatorio para estimar la correlación entre las variables latentes. En cualquier caso, se trata se verificar cuanto ajustan los datos a partir de un modelo teórico de supuestas relaciones causales propuesto por el investigador.
Si el modelo obtenido indica que los datos no respaldan la teoría propuesta por el investigador, habrá que relaborar el modelo teórico para una nueva comprobación. También es necesario verificar el cumplimiento de supuestos como linealidad, normalidad, entre otros y que existan entre 15 y 20 casos por cada variable medida.18) Es posible verificar con estas ecuaciones un modelo de regresión logística obtenido a partir de un estudio de casos y controles para la identificación de factores de riesgo o pronóstico como el estudio de Alves de Oliveira.19
Ruiz20 plantea que son muchos los tipos de modelos que se pueden definir con esta metodología, entre ellos menciona la regresión múltiple con multicolinealidad, el análisis factorial confirmatorio, el análisis factorial de segundo orden, el análisis de sendero, el modelo causal completo con variables latentes, el modelo de curva latente, el análisis de mediación y los modelos multinivel, multigrupo y los basados en las medias como ANOVA, ANCOVA, MANOVA y MANCOVA.
Los puntos fuertes de estos modelos están en haber desarrollado unas convenciones que permiten su representación gráfica, la posibilidad de hipotetizar efectos causales entre las variables, la concatenación de efectos y las relaciones recíprocas entre variables.19
Análisis estadístico implicativo
El análisis estadístico implicativo es otra técnica estadística multivariadas de la minería de datos basada en la teoría de la cuasi-implicación, la inteligencia artificial y el álgebra booleana, para modelar la cuasi-implicación entre los sucesos y variables de un conjunto de datos.
Esta técnica fue creada por el francés Régis Gras (21,22,23) para solucionar problemas de la Didáctica de las Matemáticas. La misma contempla la estructuración de datos, interrelaciona sujetos y variables, la extracción de reglas inductivas entre las variables y, a partir de la contingencia de estas reglas, la explicación y en consecuencia una determinada previsión en distintos campos del saber.
Con esta técnica se estiman las frecuencias absolutas de ocurrencia de cada variable, sus medias y desviaciones estándares, las frecuencias de ocurrencias de cada par de variables que se pueden formar, así como sus coeficientes de correlación, los índices de similaridad, de cohesión implicativa y de implicación inclusión, las tipicalidades y contribuciones de los individuos. Los resultados se presentan en tres gráficos que facilitan la interpretación de los mismos: los árboles de similaridad y de cohesión y el grafo implicativo que puede ser general y también en modo cono, según decida el investigador. Si se fuera a ubicar esta técnica dentro de la clasificación de las técnicas empleadas con regularidad, (Figura 1) se diría que es una técnica mixta.
Varias investigaciones recientes han identificado las ventajas de esta técnica y han validado su efectividad en la identificación de factores pronósticos y han verificado una utilidad mayor al emplearse previo a la regresión logística ya que aporta otro criterio para decidir cuales covariables incluir en el modelo de regresión.24,25,26,27,28,29,30,31,32
Análisis multivariado espacial
La dimensión espacial también es relevante, en los estudios de la causalidad en Ciencias Médicas, para resumir estructuras de covarianza e identificar patrones espaciales, lo cual constituye un desafío desde el punto de vista estadístico. Unas variedades de métodos han sido desarrolladas para incorporar la información espacial como el basado en índices de autocorrelación espacial, el semivariograma a partir de una variable sintética resumen, los mapas sintéticos mediante la interpolación de los valores obtenidos por la predicción de los valores de una variable aleatoria sobre un conjunto de puntos definidos por una localización en el espacio, entre otros.33
Los métodos gráficos multivariados fueron desarrollados por Sagaró y Zamora,34 de igual forma los métodos avanzados que se emplean de conjunto con las técnicas multivariadas para garantizar la validez de los estudios observacionales de causalidad en salud fueron abordados por estas autoras en otro artículo, así como otros detalles en relación al surgimiento de estas técnicas.35,36
CONCLUSIONES
Aunque las técnicas estadísticas multivariadas más empleadas en el estudio de la causalidad son las explicativas, como la regresión y los modelos estructurales, a veces es necesario un primer análisis exploratorio donde se hace necesario el empleo de las técnicas multivariadas descriptivas, por lo que es importante conocer todas las técnicas y en qué momento emplearlas. Se propone el análisis estadístico implicativo como técnica multivariada de uso habitual en las investigaciones médicas para la determinación de factores de riesgo y pronósticos por sus bondades descriptivas, explicativas y predictivas, además de sus prestaciones gráficas, que permiten visualizar las relaciones entre un conjunto de variables