ARTÍCULO ORIGINAL

 

 

Sistemas contra incendios para industria petrolera. Parte 1: Modelos de radiación térmica

 

Oil industry fire extinguishing system design. Part 1: Thermal radiation models

 

 

Dr. Eric Cabrera Estupiñán ^I, Ing. Alejandro Alomá Barceló ^II

^I Universidad Laica «Eloy Alfaro» de Manabí ULEAM, extensión Chone, Ecuador.
^II Empresa de Ingeniería y Proyectos del Petróleo, EIPP, Habana.

 

 

---

RESUMEN

En esta primera parte del trabajo se realiza un detallado análisis de los principales modelos empleados para el cálculo de la intensidad de radiación térmica incidente en un objeto producto de un incendio tipo charco. El modelo de fuente puntual (MFP) es más simple que el modelo de llama sólida (MLLS), por lo tanto sus resultados son más conservadores, lo que garantiza un mayor grado de seguridad en los diseños. Por tal motivo se adopta el MFP como modelo de cálculo. Se define el valor de I =10 kW/m² como intensidad de radiación límite para el criterio de vecindad entre tanques. También se analizan los criterios prácticos que se han venido utilizando en la Empresa de Ingeniería y Proyectos del Petróleo (EIPP) para la definición de la vecindad entre tanques.

Palabras clave: incendio tipo charco, modelo de fuente puntual, modelo de llama sólida, radiación térmica, vecindad entre tanques.

---

ABSTRACT

In this first part of the study a detailed analysis of the main models used to calculate the intensity of thermal radiation incident on an object produced by a large pool fire is performed. The point source model (MFP) is simpler than the solid flame model (MLLS), therefore its results are more conservative, ensuring greater safety in design. Therefore the MFP is assumed as the calculation model. The value I =10 kW/m² is defined as thermal radiation intensity limit for the neighbor tank criterion. Practical approaches that have been used in the Company of Engineering and Petroleum Projects (EIPP) for defining the neighbor tank criterion are also discussed.

Keywords: large pool fire, point source model, solid flame model, thermal radiation, neighbor tank criterion.

---

 

 

INTRODUCCIÓN

La industria del petróleo es sin lugar a dudas una de las más vulnerables a la ocurrencia de incendios debido al manejo de sustancias inflamables y combustibles que en ella se realiza. Es por eso que los sistemas contra incendios (SCI) tienen una importancia vital en este tipo de industria.

Fundamentalmente en los grandes emplazamientos destinados al almacenamiento de sustancias combustibles se producen incendios de tipo charco o pool fire como se le conoce en idioma inglés, ya que se desarrollan sobre la superficie líquida de los tanques que almacenan el combustible, Alomá (2013).

Cuando se diseñan los SCI de estos emplazamientos se protege toda la instalación y especialmente cada uno de los tanques en los que eventualmente pudiera ocurrir un incendio y cuando se analiza la protección general de la instalación se deben concebir escenarios de incendios en los que se tenga en cuenta la posición espacial relativa de cada uno de los tanques, ya que si hay un tanque muy cercano al que está en llamas, es muy probable que a este se le deba aplicar agua a parte o a toda la pared perimetral. Esto se conoce como vecindad de tanques y es muy importante en el diseño de los SCI en la industria del petróleo.

En Cuba existe la Empresa de Ingeniería y Proyectos del Petróleo (EIPP) en donde se realizan todos los proyectos de ingeniería referentes al campo del petróleo en la isla. Dentro de esta empresa existe un grupo de especialistas que se dedican fundamentalmente a realizar diseños y análisis de SCI.

Hasta la realización de esta investigación en la EIPP se venían empleando criterios prácticos para la definición de la vecindad entre tanques, criterios extraídos de diferentes normas, y de los cuales no se tiene un basamento claro, incluso varias de las normas más actuales recomiendan basar esta decisión en modelos de simulación de la radiación térmica pero no se cuenta con el conocimiento y las herramientas necesarias para hacer este tipo de análisis. En ese sentido va dirigida esta primera parte de la investigación. Primeramente se analizan los criterios prácticos que se han venido utilizando y posteriormente se analizan los principales modelos basados en la radiación térmica que llega a un objeto (tanque vecino) desde un tanque incendiado y se establecen criterios para la definición de vecindad entre tanques incendiados, en este sentido es de destacar el aporte realizado en la isla por Bustamante (2012).

ANALISIS DE CRITERIOS DE VECINDAD

Intensidad de la radiación térmica
El análisis de vecindad entre tanques se realiza en las etapas tempranas del proyecto de un SCI y tiene como objetivo definir las zonas a proteger de la radiación térmica producida por un incendio en alguno de los depósitos de combustible. Esta protección se ejecuta comúnmente en depósitos que se localizan dentro de esta zona de riesgo y consiste en el enfriamiento parcial o total de las paredes de estos.

La intensidad de la radiación térmica por unidad de superficie que es recibida por un objeto a una distancia determinada es entonces el factor que define los criterios de vecindad que se verán en lo adelante. Esta variable se expresa en unidades kW/m². Para que se tenga una idea de su valor, en un día de verano soleado una persona puede llegar a estar expuesta a un máximo de radiación de 1 kW/m². Una exposición prolongada bajo dichas condiciones puede producir daños considerables en los seres humanos (González et al. 2002).

En IR-S-02 (1993) se definen valores de intensidad de radiación térmica que pueden ayudar a comprender y sobre todo a fijar cotas límites de radiación permisibles en depósitos para almacenamiento de combustible sin que sean afectados, ver tabla 1.

En esta misma referencia se presenta la tabla 2 en la que se cuantifican porcentualmente los daños a equipos producto de determinados valores de intensidad de radiación térmica.

En McGrattan et al. (2000) se define el criterio de distancia de separación aceptable para incendios, sus siglas en inglés son (ASD). En esta referencia se definen dos criterios, uno para edificaciones y otro para personas, en el primer caso la edificación comenzará a sufrir daños serios para valores de intensidad de radiación mayores o iguales que 31,5 kW/m², en el segundo caso este valor es 1,4 kW/m².

Criterios de vecindad empleados en la EIPP

La EIPP tiene como principal función la realización de proyectos de ingeniería para la industria del petróleo en Cuba. Disimiles son los proyectos que se realizan allí, destacándose los diseños de sistemas contra incendios ya que prácticamente todos los proyectos tecnológicos necesitan invariablemente de un SCI.

El grupo de ingenieros hidráulicos que tiene a su cargo el diseño de los sistemas contra incendio SCI, ha acudido históricamente a criterios que de una forma pragmática definen la vecindad entre depósitos de combustible. Está muy extendido el uso de diferentes normas, criterios o medidas tradicionales las cuales se caracterizan por su escueta explicación científica y por su diversa procedencia (Alomá 2013).

Por ejemplo, NC 96-02-18 (1987) establece que se deben considerar como vecinos los depósitos que se encuentren a una distancia (medida entre paredes) de una vez el diámetro del tanque incendiado, sin distinción del tipo de combustible almacenado.

Durante la década de los 90 del pasado siglo en la EIPP y la agencia de protección contra incendios (APCI) de Cuba, se empleó un criterio de vecindad basado en la clasificación de las sustancias en claras y oscuras. Para sustancias oscuras se debía proteger a los depósitos que se encontraran a una distancia de una vez el radio del depósito incendiado y para productos claros y crudos 0,75 veces el diámetro del depósito incendiado, no pudiendo ser menor de 25 m. Dicha distancia se define entre las paredes de los tanques (Alomá 2013).

En IR-M-03 (1983) se plantea un criterio muy interesante que puede ser resumido en considerar tanques vecinos a los que se encuentren dentro de un círculo concéntrico (al tanque incendiado) de un radio igual a 2D, siendo D el diámetro del tanque incendiado. Es importante destacar que en esta referencia se brinda este valor (2D) como alternativa ante la imposibilidad de aplicar modelos de cálculo de radiación térmica, siendo esta herramienta la más aconsejable para abordar dicha problemática.

Este criterio, conocido en lo adelante como (2D) es el que se ha venido aplicando últimamente en la EIPP.

Si bien estos criterios son de muy fácil aplicación y muy prácticos, existe una diferencia significativa entre ellos. Además ninguno evalúa directamente los efectos reales de la radiación térmica. Por esa razón se considera que la aplicación de modelos de cálculo de radiación debe ser una herramienta indispensable para la definición de la vecindad entre tanques y los criterios antes analizados pudieran ser empleados como elementos adicionales.

MODELOS DE CÁLCULO DE LA INTENSIDAD DE LA RADIACIÓN TÉRMICA

En este trabajo se analizan solo los incendios producidos en tanques de almacenamiento de combustibles, a este tipo de incendios la bibliografía especializada los nombra incendios de charco o en inglés pool fire (TNO 2005).

Un incendio de este tipo ocurre porque una fuente de calor es introducida en la zona superior de la superficie libre de la sustancia combustible, donde se están generando gases constantemente y donde también hay oxígeno que es el agente oxidante de esta reacción química llamada combustión. Esta superficie libre se puede ver espacialmente como un charco circular ya que es la forma que tienen estos tanques de acero. En ocasiones el incendio provoca la rotura del tanque o de alguna forma se derrama (fuera del tanque) combustible en llamas el cual es contenido en el cubeto de protección y se mantiene el mismo tipo de incendio de charco (González et al. 2002).

Para los distintos tipos de incendios se han desarrollado varios modelos de cálculo, en la tabla 3 se presentan los más conocidos.

De todos estos modelos los más utilizados son el de fuente puntual (MFP), que es el de mayor sencillez, y el de llama sólida (MLLS) que tiene la característica de ser más riguroso al adaptarse mejor a la realidad del fenómeno (González et al. 2002).

La magnitud de la radiación térmica emitida depende de numerosos factores que se pueden agrupar de la siguiente forma:

- Propiedades del combustible: entalpías de combustión y de vaporización, temperatura de ebullición y calor específico del líquido.

- Características de la llama: temperatura, potencia emisiva específica y geometría (altura de la llama y diámetro del charco).

- Otros procesos químicos implicados en la combustión: formación de humos y productos gaseosos parcialmente quemados que disminuyen la potencia emisiva de la llama.

La naturaleza de la sustancia y las características geométricas de la llama juegan un papel fundamental en la intensidad de radiación térmica. La primera porque determina el caudal de vapor que se incorpora al incendio, aunque también depende de los mecanismos de evaporación que tienen lugar durante el evento, y la segunda porque caracteriza las dimensiones del foco emisor. Así, por ejemplo, en el caso de incendios confinados, la superficie de la base de la llama está determinada por el área de confinamiento depósito, cubeto, mientras que, por el contrario, si no existe confinamiento la superficie del charco puede sufrir variaciones importantes desde que se inicia la fuga o derrame hasta que se produce la ignición, alcanzando un máximo que posteriormente decrece a medida que se consume el producto (CPQRA 2000).

Por otro lado, la radiación térmica recibida por un objeto depende también de las características del receptor (tipo, dimensiones, ubicación y orientación respecto de la llama) y de las condiciones atmosféricas (la humedad y el dióxido de carbono disminuyen la transmisividad de la radiación y el viento refrigera el objeto e inclina la llama (González et al. 2002).

Modelo de fuente puntual (MFP)

Este modelo tiene un grupo de hipótesis que se enumeran a continuación:

1- El proceso de combustión se concentra en un punto, desde donde se emite toda la energía radiante.

2- Para cada sustancia la energía radiada es una fracción de la energía total producida en el proceso de combustión.

3- La propagación de la radiación sigue una geometría esférica, teniendo como origen el punto donde se supone concentrado el incendio.

Con todas estas consideraciones se tiene que en el MFP la intensidad de radiación incidente en un objeto ubicado a una distancia x del centro del tanque se puede calcular con la siguiente ecuación:

donde:

I_(x) : Es la intensidad de radiación incidente en un objeto ubicado a una distancia x en m del centro del tanque, se expresa en kW/m².

τ_a : Coeficiente de transmisividad atmosférica. Varía entre 0 1, es adimensional.

F_s : Fracción de la energía radiada. Es adimensional y difícil de obtener, varía entre 0,1 0,4.

m' : Caudal másico evaporado por unidad de superficie, kg/m²s, en inglés «burning rate».

S : Área del charco incendiado, m².

ΔH_c: Entalpía de combustión, kJ/kg. Es la cantidad de energía total en forma de calor que será capaz de emitir durante el proceso de combustión cada kg de la sustancia que se esté modelando.

x: Distancia desde el centro de la llama en el charco hasta el objeto receptor, m.

En la ecuación (1), el coeficiente de transmisividad atmosférica τ_a tiene una dependencia de x y de varios factores atmosféricos según TNO (2005).

donde: a_w y a_c son coeficientes adimensionales de absorción de vapor de agua y de dióxido de carbono respectivamente, ya que estos son los principales componentes del aire que absorben radiación térmica. Es conocido que a_c en muy pequeño en relación con su similar a_w por lo tanto, es práctica común despreciarlo o tomar un valor constante, (González et al. 2002).

En relación con el coeficiente a_w en González et al. (2002) se brinda un gráfico en el que se puede obtener el valor de a_w si se tiene el producto entre P_w y x, (P_w se define más abajo). En este gráfico existen varias curvas, cada una para una temperatura de la llama determinada. En esta misma referencia se afirma que dicha temperatura es generalmente desconocida y es práctica común emplear un valor intermedio 1200 K. Siguiendo esta lógica se obtuvo una ecuación de mejor ajuste extrapolada para esta curva, la que se presenta como ecuación (3).

donde: a= 0,02301848; b=0,0018476; c= 5,3036*l0^-6; d=9,658*10^-9; e= 1,062*10^-11; f=6,41567*10^-15, g= 1,6239*10^-18.

Para el cálculo de la presión parcial de vapor de agua en el aire P_w se presentan las ecuaciones (4) y (5), las que se encuentran en TNO (2005) y CPQRA (2000) respectivamente.

donde:

P_w : Presión parcial de vapor de agua en el aire en Pa.

P_wo : Presión de vapor saturado de agua en aire en Pa.

Hr : Humedad relativa, expresada en %.

Ta : Temperatura ambiente expresada en Kelvin.

Modelo de llama sólida (MLLS)

El MLLS fue propuesto inicialmente por Raj (1977) citado por CPQRA (2000) para incendios de charco, aunque se ha extendido a cualquier tipo de incendio y actualmente constituye una de las metodologías más rigurosas para la determinación de la intensidad de la radiación incidente.

Acorde con CPQRA (2000) su idoneidad se fundamenta en la modelación realista de la llama y parte de los siguientes supuestos:

1- La llama se representa con geometrías tridimensionales sencillas tales como cilindros, láminas, esferas, conos, etc, cuyas dimensiones se corresponden con las del incendio.

2- La energía radiante se emite uniformemente a través de la superficie exterior de la llama, considerando como emisor sólo la zona visible de esta.

Con estas consideraciones se tiene que en el MLLS la intensidad de radiación incidente en un objeto ubicado a una distancia x del centro del tanque se puede calcular con la ecuación (6).

donde:

F_máx : Es el llamado factor de visión máxima y es adimensional.

SEP_act : Potencia emisiva superficial actual en kW/m².

El factor de visión máxima F_máx puede estimarse con la ecuación (7) en la que F_h es la componente visual en el eje horizontal y F_v es la componente visual en el eje vertical.

El factor de visión F_máx se estima a partir de expresiones generalmente complejas, que dependen de ciertas relaciones geométricas de la llama, de la distancia al objeto expuesto, así como de la orientación relativa de ambos (Fleury 2010).

El MLLS suele configurarse como un cilindro cuya base corresponde a la superficie del charco, considerada circular y su altura es la alcanzada por las llamas.

En este modelo es común definir dos casos, el primero llamado MLLS sin presencia de viento y el segundo MLLS con presencia de viento, figura 1 casos (a) y (b) respectivamente.

En ambos casos R en m y D en m son el radio y el diámetro del tanque incendiado, x en m es la distancia desde el centro del depósito hasta el objeto que está recibiendo radiación. En el caso del esquema sin presencia de viento la altura promedio de la llama L en m es vertical, ver figura 1 caso (a), sin embargo en el caso del esquema con presencia de viento, esta altura sigue la configuración de la llama, es decir en la dirección que fija el ángulo θ, medido desde la dirección vertical. Finalmente u_w es la velocidad del viento, ver figura 1 caso (b).

Modelo MLLS sin presencia de viento, ver TNO (2005)

Para calcular la altura L promedio de la llama se han propuesto muchos modelos, de forma general para llama visible y condiciones de calma se puede emplear la ecuación de Thomas de 1963 citado por TNO (2005), en la que la relación L/D es una función de m', ρ_a, D.

donde:

ρ_a : Es la densidad del aire en kg/m³.

g : Es la aceleración de la gravedad en m/s².

D : Es el diámetro del tanque en m.

Modelo MLLS con presencia de viento, ver TNO (2005)

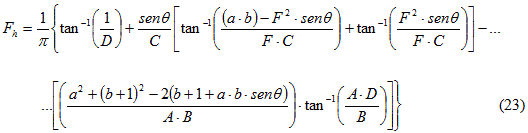
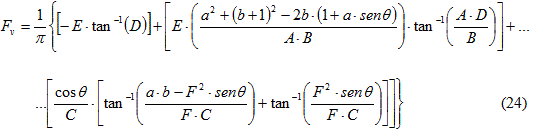
Para calcular la altura L promedio de la llama bajo condiciones de viento en la ecuación de Thomas se incluye la dependencia del término u^* que se conoce como velocidad adimensional del viento, para este caso la ecuación (14) se transforma en la (25).

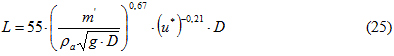
Para poder obtener el valor de u^* es necesario definir la llamada velocidad característica del viento u_c en m/s. en la ecuación (26).

Si u_w < u_c entonces u^*=1, de no ser así u^*=u_w/u _c

Para velocidades del viento mayores que el valor característico, la altura de la llama tiende a mantenerse constante.

Para el cálculo del ángulo de inclinación de la llama con respecto a la vertical θ se puede emplear primeramente la estrategia recomendada por la American Gas Association (1974), citada por TNO (2005) en la que si u^* ≥ 1 entonces este ángulo se obtiene aplicando la ecuación (27), de no ser así u^*<1 y en estas condiciones cosθ=1, luego θ=0 (condiciones de calma), ver González et al (2002).

En TNO (2005) también se propone la ecuación (28).

Donde el parámetro «c» puede ser calculado mediante la ecuación (29) en la cual los coeficientes a^', b^', c^' y d' vienen dados en la tabla 4 para diferentes condiciones.

donde:

N_F : Es el número de Froude, parámetro adimensional.

N_R : Es el número de Reynolds, parámetro adimensional.

ρ_v : Es la densidad del vapor del combustible en kg/m³.

υ_a : Es la viscosidad cinemática del aire en m²/s.

Hasta aquí se puede calcular el término F_máx de la ecuación (6) para las condiciones de calma y de viento. Finalmente se calcula la potencia emisiva superficial actual según ecuaciones (32) y (33).

donde:

SEP_máx : Potencia emisiva superficial máxima en kW/m².

SEP_soot : Potencia emisiva superficial de hollín en kW/m².

Acorde con TNO (2005) su valor puede fijarse en 20 kW/m².

ζ: Acorde con TNO (2005) para incendios de charco se puede aceptar 0.8.

APLICACIÓN DE LOS MODELOS

Datos del combustible:

Combustible: Fuel

-oil, ρ_comb=995,9 kg/m³, ΔH_c=39800 kJ/kg, m'=0,035 kg/m²s.

Datos del tanque:

D= 58 m (diámetro), H=18,75 m (altura), Vol=50000 m³ (volumen).

Datos atmosféricos:

Hr=80%, Ta=28º C, ρ_aire=1,1732 kg/m³, υ_aire= 1,327*10^-5 m²/s, P_wo= 3994,29 Pa, u_w=5 m/s (solo para el caso de MLLS con presencia de viento).

Otros:

F_s= 0,4, SEP_soot= 20 kW/m², ζ=0.8

 

RESULTADOS

En el caso del MFP se calcula la presión parcial de vapor de agua en el aire mediante la ecuación (4), P_w= 3195,43 Pa.

En el caso del MLLS sin la presencia de viento se calcula la altura promedio de la llama mediante la ecuación (14), L=41,30 m, además se calculan SEP_máx =144,80 kW/m² y SEP_act =44,96 kW/m².

En el caso del MLLS con la presencia de viento se obtienen los siguientes valores, u_c=2,57 m/s, u^*=1,945 m/s, L= 31,49 m, el ángulo de inclinación de la llama calculado por las expresiones (27) y (28) es θ= 44,20º y θ= 48,43º respectivamente, para la expresión (28) se obtuvo que N_F= 0.439 y N_R= 21851066, además se calculan SEP_máx=175,68 kW/m² y SEP_act= 51,15 kW/m².

Los demás parámetros tienen una dependencia con la x (en m) y en este sentido se realizó una variación de esta variable desde la pared del tanque hasta unos 190 m obteniéndose los valores de intensidad de radiación incidente I_(x) en cada punto. Todo esto fue realizado para los tres modelos, los resultados pueden apreciarse en la figura 2.

Obsérvese que todas las gráficas comienzan a una distancia de 29 m desde el centro del tanque, esta posición es precisamente la pared del tanque. En este punto los modelos MLLS con viento y sin él, tienen valores de I cercanos 35.40 y 22.39 kW/m² respectivamente, sin embargo el MFP tiene un valor muy superior a los anteriores 101.55 kW/m². A medida que se aumenta la distancia del objeto receptor al emisor todos los modelos tienden a converger debido a que la influencia de la geometría de la llama es cada vez menor.

Partiendo de los valores que se encuentran en la tabla 1, se adopta como un valor conservador para definir el criterio de vecindad entre tanques 10 kW/m². Es decir los tanques que estén expuestos a un valor de intensidad de radiación mayor o igual que 10 kW/m² se consideran vecinos del incendiado.

En la gráfica 2 se puede observar que este valor de I=10 kW/m² se obtiene a los 21 m, 39 m y 61,50 m medidos desde la pared del tanque incendiado, según los modelos MLLS sin viento, MLLS con viento y MFP. Como puede observarse las diferencias son apreciables.

Siguiendo este análisis se decidió repetir el procedimiento para varios tanques de almacenamiento de combustible. Los resultados están recogidos en la tabla 5.

Las primeras tres columnas de la tabla 5 están referidas al volumen, altura y diámetro del tanque, las siguientes tres columnas son referidas a los modelos de fuente puntual, de llama sólida sin viento y de llama sólida con viento, las últimas tres pertenecen a los criterios de separación entre tanques de una vez el diámetro, una vez el radio (por ser el Fuel-oil un producto oscuro) y dos veces el diámetro pero medido este último desde el centro del tanque. Para estos cálculos se emplean los mismos datos que los del ejemplo anterior.

Es importante hacer notar que las variaciones entre tanques influyen en este tipo de análisis con la variación del diámetro, a medida que este aumenta así lo hace el área del charco que es donde se desarrolla el incendio. Por ejemplo en el caso del tanque de 30000 m³ y el primer tanque de 50000 m³, a pesar de la diferencia en volúmenes ambos tienen diámetros parecidos y por ende los resultados son también similares, ver tabla 5.

El MFP tiene la ventaja de ser más simple que el MLLS ya que concibe la fuente de radiación como un punto y desprecia todas las características geométricas de la llama. Por ser un modelo menos riguroso, sus resultados son más conservadores, lo que aporta un cierto margen de seguridad desde el punto de vista práctico a la hora de definir tanques vecinos. Además el MLLS brinda valores muy pequeños de distancia entre tanque incendiado y vecinos, en comparación con los criterios analizados, en algunos casos hasta de la mitad del radio del tanque incendiado, ver en tabla 5 el tanque de 10000 m³. Este es un criterio que debe aplicarse con mucha cautela porque sin dudas encierra un peligro evidente.

Por otra parte están los criterios 1D y 2D. Obsérvese cómo los resultados obtenidos por el modelo de simulación MFP para todos los tanques son muy similares a los obtenidos según el criterio práctico 1D, tabla 5 columnas 4 y 7, sin embargo sería un error pensar que esto se repite para todos los combustibles. A continuación se realiza el mismo ejemplo pero cambiando la sustancia almacenada en el tanque incendiado, en este caso se tiene petróleo crudo.

Segundo ejemplo

Datos del combustible:

Combustible: Petróleo crudo, ΔH_c=42600 kJ/kg, m'=0,045 kg/m²s.

Datos del tanque:

D= 58 m (diámetro), H=18,75 m (altura), Vol=50000 m³ (volumen).

Datos atmosféricos:

Hr=80%, Ta=28º C, ρ_aire=1,1732 kg/m³, υ_aire= 1,327*10^-5 m²/s, P_wo= 3994,29 Pa.

Al aplicar el MFP, el valor de I=10 kW/m² se obtiene a los 76 m de la pared del tanque incendiado, valor que se aleja del criterio 1D que es 58 m y también está alejado del valor 61,50 m que es el obtenido aplicando el MFP cuando el fluido es Fuel-oil. Más bien el valor aquí obtenido se acerca al criterio 2D, con lo cual se demuestra que al considerar sustancias con mayores valores de entalpía de combustión y de caudal másico evaporado por unidad de superficie los valores de intensidad de radiación serán mayores y por lo tanto la isolínea de I=10 kW/m² se acercará más a la definida por el criterio 2D. Este resultado es muy importante porque le permite a los especialistas tener una idea de qué criterio práctico pudiera tomarse en cuenta en un incendio según el tipo de sustancia que esté en combustión, 1D, 2D u otro de los analizados. Sin embargo los autores consideran que estos análisis no deben realizarse sin el empleo de modelos de simulación de la intensidad de radiación que son las herramientas más eficaces y precisas para ayudar a definir el criterio de vecindad entre tanques.

Se considera entonces el uso del MFP como herramienta básica para la definición del criterio de vecindad y como apoyo los criterios prácticos 1D, 2D u otros. Estas son recomendaciones directas para los especialistas de la EIPP que tienen que diseñar sistemas contra incendios de este tipo.

Debido a la gran diferencia que existe entre las posibles soluciones se considera muy importante la experiencia del especialista y un análisis profundo y particularizado de cada escenario de incendio (ver segunda parte del artículo). También es muy importante en estos casos las decisiones que pueda tomar el consejo técnico asesor de la entidad inversionista (cliente) con las autoridades de la APCI y el Cuerpo de Bomberos, siempre que estas impliquen soluciones más conservadoras.

CONCLUSIONES

· Se realiza un análisis de los principales criterios prácticos de vecindad que se han venido empleando por los especialistas de la Empresa de Ingeniería y Proyectos de Petróleo de Cuba (EIPP). Criterios prácticos que están en función del diámetro del tanque incendiado y cuyo basamento teórico no se ha encontrado. En este sentido varias normas sugieren el empleo de modelos de radiación térmica como herramienta de apoyo para resolver este problema.

· Se adopta el valor de I=10 kW/m² como intensidad de radiación límite para el criterio de vecindad (entre tanques para almacenamiento de combustible), con el empleo de modelos de radiación térmica.

· Se realiza un detallado análisis de los principales métodos empleados para el cálculo de la intensidad de radiación incidente en un objeto producto de un incendio de tipo charco, modelo de fuente puntual MFP y modelo de llama sólida MLLS. De este análisis se puede concluir lo que se expresa a continuación.

· El modelo de fuente puntual (MFP) tiene la ventaja de ser más simple que el MLLS ya que concibe la fuente de radiación como un punto y desprecia todas las características geométricas de la llama. Por ser un modelo menos riguroso, sus resultados son más conservadores, lo que aporta un cierto margen de seguridad desde el punto de vista práctico a la hora de definir tanques vecinos. Además el MLLS brinda valores muy pequeños de distancia entre tanque incendiado y vecinos. Este es un criterio que debe aplicarse con mucha cautela porque sin dudas encierra un peligro evidente.

· Se demuestra que al considerar sustancias con mayores valores de entalpía de combustión y de caudal másico evaporado por unidad de superficie los valores de intensidad de radiación serán mayores y por lo tanto la isolínea de I=10 kW/m² se acercará más a la definida por el criterio 2D. Este resultado es muy importante porque le permite a los especialistas tener una idea de qué criterio práctico pudiera tomarse en cuenta en un incendio según el tipo de sustancia que esté en combustión. Sin embargo los autores consideran que estos análisis no debe realizarse sin el empleo de modelos de simulación de la intensidad de radiación que son las herramientas más eficaces y precisas para ayudar a definir el criterio de vecindad entre tanques.

· Se propone el empleo del MFP como herramienta básica para la definición del criterio de vecindad y como apoyo los criterios prácticos 1D, 2D u otros. Estas son recomendaciones directas para los especialistas de la EIPP que tienen que diseñar sistemas contra incendios de este tipo.

· Debido a la gran diferencia que existe entre las posibles soluciones, se considera muy importante la experiencia del especialista y un análisis profundo y particularizado de cada escenario de incendio. También es muy importante en estos casos las decisiones que pueda tomar el consejo técnico asesor de la entidad inversionista (cliente) con las autoridades de la APCI y el Cuerpo de Bomberos, siempre que estás impliquen soluciones más conservadoras.

Nota: En la segunda parte de este trabajo se presenta y aplica un programa para el cálculo de la radiación térmica basado en los modelos analizados aquí y con una concepción enfocada a las necesidades de los proyectos de sistemas contra incendios.

RECONOCIMIENTOS

Se realiza un reconocimiento especial a los siguientes especialistas de la Empresa de ingeniería y proyectos del petróleo de Cuba EIPP, que contribuyeron de una forma importante para la realización de este estudio: Ing. Ileana Rodríguez Ordaz; Ing. Alejandro Omar Cueto Alonso; Ing. Daismel Díaz Domínguez; Ing. Angel Echevarría Roque.

Se reconocen los aportes y consejos del especialista de la Agencia de protección contra incendios (APCI) de la Habana, Ing. Felipe J. Bustamante García.

También a las autoridades de la Empresa de Ingeniería y Proyectos del Petróleo de Cuba (EIPP), del Centro de Investigaciones Hidráulicas (CIH) de la CUJAE, Cuba y de la Universidad Laica «Eloy Alfaro» de Manabí, extensión Chone, Ecuador.

 

 

REFERENCIAS BIBLIOGRÁFICAS

Alomá B. A. «Integración de modelos para el cálculo de la radiación térmica y del flujo a presión en redes de tuberías para el diseño de Sistemas Contra Incendios en la industria del petróleo». Tesis de pregrado, Facultad de Ingeniería Civil. Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana, Cuba. (2013).

Bustamante G. F. «Cálculos de Flujo de Calor de Radiación (Versión 1.03)». Guía de referencia técnica. Agencia de Protección Contra Incendios APCI, Habana, Cuba. (2012).

CPQRA «Chemical Process Quantitative Risk Analysis». Second Edition. Center for Chemical Process Safety of the American Institute of Chemical Engineers. 3 Park Avenue, New York, USA. (2000).

Fleury R. «Evaluation of thermal radiation models for fire spread between objects». Master of Engineering thesis in Fire Engineering. Department of Civil and Natural Resources Engineering, University of Canterbury. Christchurch, New Zealand. (2010).

González F. E., Ruiz F. J., Miñana A. A., Navarro G. J., Ruiz G. J y Martínez A. J. «Zonas de planificación para accidentes graves de tipo térmico (en el ámbito del Real Decreto 1254/99(Seveso II)». Departamento de Ingeniería Química. Universidad de Murcia. Dirección general de protección civil, Ministerio del Interior. España. (2002).

IR-M-03 «Sistema de agua contra incendio», PDVSA-Petróleos de Venezuela, SA. Caracas, Venezuela. (1983).

IR-S-02 «Criterios para el análisis cuatitativo de riesgos», PDVSA-Petróleos de Venezuela, SA. Caracas, Venezuela. (1993).

McGrattan B. K., Baum R. H. and Hamins A. «Thermal radiation from large pool fires». National Institute of Standards and Technology. U.S. Department of Commerce. USA. (2000).

NC 96-02-18 . «Bases de almacenamiento de petróleo y sus derivados». Sistema de normas de protección contra incendios. Comité Estatal de Normalización. Nivel Central. Cuba. (1987)

TNO «Methods for the calculation of physical effects due to releases of hazardous materials (liquids and gases)», Yellow Book CPR-14E. The Netherlands Organization of Applied Scientific Research. Holland. (2005).

 

 

Recibido: 1 de enero de 2015.
Aprobado: 10 de abril de 2015.

 

 

Dr. Eric Cabrera Estupiñán, Ing. Alejandro Alomá Barceló, Universidad Laica "Eloy Alfaro" de Manabí ULEAM, extensión Chone, Ecuador, Empresa de Ingeniería y Proyectos del Petróleo, EIPP, Habana, email: [e-mail], email: [e-mail]