ARTÍCULO ORIGINAL

 

 

Simulación matemática de la interacción oleaje-estructuras de protección costera

 

Mathematical simulation of the interaction wave-coastal protection structures

 

 

Kenia Hernández Valdés ^I, Luis F. Córdova López ^II

^I Inversiones Gamma S.A. Playa. La Habana, Cuba.
^IICentro de Investigaciones Hidráulicas. Instituto Superior Politécnico José Antonio Echeverría (Cujae). La Habana.

 

 

---

RESUMEN

El aumento creciente de la población en la zona costera unido al incremento y desarrollo de las inversiones asociadas al turismo de sol y playa, hacen que cada día cobre mayor importancia conocer el comportamiento de la interacción entre el oleaje y las estructuras de defensa costera, junto con la necesidad de pronosticar de forma rápida y correcta los procesos morfodinámicos que ocurren en las playas de arena ante situaciones extremas. Elpresente trabajo evalúa la capacidad del modelo matemático XBeachpara simular de forma correcta la interacción oleaje estructuras de protección costera, fundamentalmente la capacidad del modelo para reproducir los fenómenos asociados con la hidrodinámica y los cambios morfológicos en presencia de obras como espigones y rompeolas.

Palabras clave: espigones, estructuras de protección costera, modelación matemática, rompeolas.

---

ABSTRACT

The significant increase of the population in coastal areas togetherwith the increment and development of the investments associated to sun and beach tourism, make that every day becomes moreimportant torecognize the behavior of the interaction between wave and coastal defense structures, together with the necessity to predict in a quick and correct way the morphodynamicprocessesocurringin sandbeaches under extreme situations. The present work evaluates the capacity of the mathematicalmodelXbeachto correctly simulatethe wave-coastal protection structures interaction, mainly its capacityto reproduce the phenomena associatedwith the hydrodynamic and morphology changes in the presence of groin sand breakwaters.

Keywords: groins, coastal protection structures, mathematical modeling, breakwaters.

---

 

 

INTRODUCCIÓN

Hoy en día bajo el contexto del cambio climático global, numerosos factores asociados al calentamiento atmosférico y al ascenso del nivel medio del mar han dado lugar a un aumento de la incidencia y la intensidad de las tormentas que afectan el área geográfica, así como a la generalización de los problemas erosivos (Cabrera et al. 2011), (EIRD 2003). Esta situación conduce a la necesidad de evaluar con antelación cuál será la respuesta morfológica de las playas ante estos eventos.

Con el objetivo de conocer la vulnerabilidad de la zona costera y diseñar actuaciones para su manejo y protección, se han desarrollado modelos matemáticos que hacen posible la toma de decisiones ante la presencia de situaciones extremas(Córdova y Valdés 2011).

Especialistas de la UNESCO-IHE Institute for Water Education, Delft University of Technology y Deltares, han desarrollado el modelo numérico XBeach(Roelvink et al. 2010) para simular la hidrodinámica litoral y la morfodinámica de la duna ante eventos extremos, lo que constituye una importante innovación en el campo de la investigación costera. Este modelo está siendo utilizado para el diseño de medidas preventivas, incluyendo defensas costeras, y para establecer medidas de protección civil, de reducción de riesgo y de evacuación de la zona litoral, como parte de un sistema de alerta temprana que integra tanto modelos hidrodinámicos como morfológicos.

Nuestro país es afectado anualmente por numerosos eventos climatológicos entre los que se destacan los frentes fríos, las bajas extra tropicales y las tormentas tropicales, que provocan severos daños en las zonas costeras(Córdova 2014). El objetivo principal de esta investigación es evaluar el comportamiento en 2D del modelo XBeach ante la presencia de obras de protección como espigones y rompeolas, analizando su capacidad de simular la hidrodinámica y la morfología en la interacción oleaje-estructuras costeras, y que constituya una herramienta de diseño para proponer actuaciones costeras en el manejo integrado de la zona litoral.

DISEÑO DEL EXPERIMENTO

Para conocer el comportamiento hidrodinámico del modelo ante la presencia de estructuras de protección costera como rompeolas y espigones, se realizaron una serie de pruebas utilizando una malla regular de 200 x 400 m de longitud, con resolución de 10 m en las direcciones perpendicular a la costa (x) y a lo largo de la costa (y), la cual presenta batimetrías rectas y paralelas.

Las pruebas realizadas incrementan progresivamente la complejidad de las modelaciones numéricas, variando las condiciones hidrodinámicas y batimétricas así como las obras costeras a modelar, describiéndose en la tabla 1 las etapas que presentaron los resultados más relevantes. La verificación del modelo tiene lugar por la comparación de los resultados con las teorías hidrodinámicas existentes.

Primera etapa

Esta etapa tiene como objetivo conocer la distribución de velocidades de las corrientes generadas por la presencia de espigones y rompeolas ubicados en la zona central de la malla de trabajo, lo que introduce variaciones en la batimetría. Para ello se modelan las estructuras con entrada del oleaje en dirección normal a la costa (270º), utilizando como condición de frontera del oleaje, fondo duro, altura media cuadrática Hrms=1m, período representativo Trep=7s, duración del evento 100horas, y variación nivel estático Zso=0.

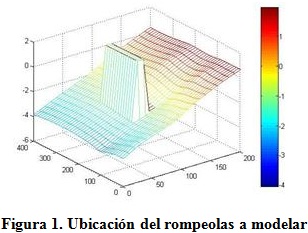
El rompeolas a modelar presenta una longitud de 140 m, un ancho de 10 m, una cota de 2 m por encima del nivel medio del mar y se ubica dentro de la zona de rompientes en profundidades que oscilan entre 2,0y 2,5 m, separado a una distancia de la costa de 100 m como se muestra en la figura 1.

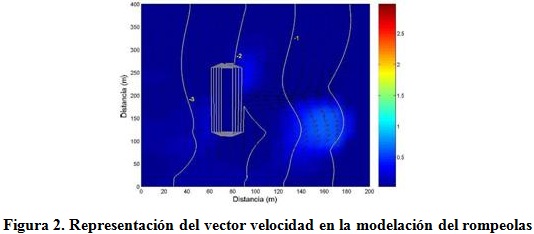
Los resultados obtenidos de la aplicación del modelo que se muestran en la figura 2 son cualitativamente correctos. En general, las alturas de olas en la zona protegida por el rompeolas son menores que en otras zonas, debido a la pérdida de energía del oleaje por la rotura y por el proceso de difracción y disipación que provoca la estructura. Las corrientes generadas muestran claramente dos celdas de circulación simétricas, transportando el agua desde la parte posterior del rompeolas hacia el frente, debido a la generación de gradientes por el tensor de radiación.

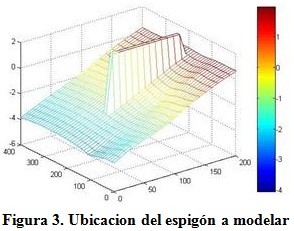
El espigón a modelar presenta una longitud de 120 m, un ancho de 10 m, una cota de 2 m por encima del nivel medio del mar y alcanza profundidades de 2,5 m, como aparece en la figura 3.

En la figura 4 se reflejan los resultados obtenidos de la aplicación del modelo, donde se producen celdas de circulación a cada lado del espigón en las que el agua fluye hacia el mar desde la playa, debido a la generación de gradientes cuando las olas se acercan en direcciónnormal y se hacen más pequeñas en las áreas adyacentes al espigón por la disipación de energía causada en la interacción del movimiento del agua con la estructura.

Conclusiones de la primera etapa

Se estudió la habilidad del modelo para trabajar con variaciones en las batimetrías debido a la presencia de rompeolas y espigones bajo la incidencia del oleaje perpendicular a la costa. Los procesos hidrodinámicos relacionados con la rotura del oleaje en estas condiciones fueron cualitativamente bien modelados por el XBeach, comportándose de manera similar a los patrones establecidos en las teorías hidrodinámicas de Gourlay(1974); MacMahan et al. (2004) yMacMahan et al. (2006).

Segunda etapa

Esta etapa tiene como objetivo obtener la distribución de velocidades de las corrientes generadas por la presencia de espigones ubicados dentro de la zona de rotura y cercanos a la costa. Para ello se modelan estas estructuras con entrada del oleaje en dirección oblicua a la costa (315º), utilizando como condición de frontera del oleaje: fondo móvil, Hrms=1m, Trep=7s, duración del evento 200h y variación nivel estático Zso=0.

El espigón, ubicado dentro de la zona de rotura del oleaje, presenta una longitud de 120 m, un ancho de 10 m, una cota de 2 m por encima del nivel medio del mar y alcanza profundidades de 2,5 m, como se muestra en la figura 3. En la figura 5 (a) pueden observarse los resultados de la modelación del vector velocidad de las corrientes durante las primeras 10 horas y en la figura 5 (b) una vez transcurridas 200 horas.

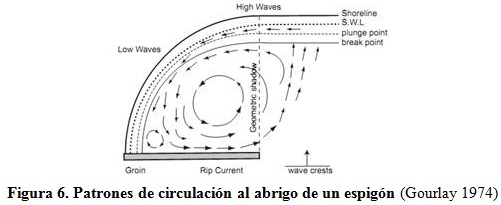
Los patrones de circulación revelaron la existencia de una corriente longitudinal debido a la incidencia oblicua del oleaje, que viaja paralela a la costa bordeando al espigón y una celda de re-circulación originada por los cambios en el setup del oleaje como resultado de las menores alturas de ola al abrigo del espigón, cuyo comportamiento es similar al descrito por Gourlay (1974) en la figura 6.

Al simular las condiciones del oleaje durante 200 horas se observa en la figura 7 (a) y (b), cómo aumentan las velocidades de circulación de las corrientes en el extremo del espigón, las que alcanzan valores del orden de 2,2 m­/s, provocando cambios en la batimetría al incrementarse el transporte de sedimentos y la aparición de socavaciones, lo que es importante considerar cuando se diseña este tipo de estructuras.

Los resultados obtenidos coinciden con investigaciones realizadas sobre los patrones de circulación al abrigo de espigones en Pattiaratchiet al.(2009), donde los autores describen la formación de las corrientes de retorno con gran potencial para el transporte de sedimentos fuera de la costa y la presencia de celdas de circulación por cambios en los gradientes del oleaje.

Por su parte los resultados de la modelación del espigón ubicadocerca de la costa, con una longitud de 60 m, un ancho de 10 m, cota de 2 m por encima del nivel medio del mar y que alcanza profundidades de 2,5 mse muestran en la figura 8 (a) y (b). Para las primeras 10 horas y una vez transcurridas 200 horas, se observa que las corrientes longitudinales que viajan paralelas a la costa, bordean el espigón continuando su rumbo aguas abajo. Debe destacarse que las velocidades de circulación que alcanzan las corrientes en el extremo del espigón se encuentran con valores sobre 0,9 m­/s y no se aprecian grandes cambios en la batimetría ni la presencia de socavaciones en la estructura. La línea de costa en el extremo aguas arriba del espigón muestra un ligero avance hacia el mar, lo que es señal del proceso de sedimentación que se produce, al convertirse en un obstáculo para el transporte de sedimentos que se mueve a lo largo del litoral.

Conclusiones de la segunda etapa

En esta etapa se estudió la habilidad del modelo para simular el comportamiento de espigones ubicados en la zona de rompiente bajo la incidencia oblicua del oleaje y con la presencia de sedimentos (fondo móvil). Los procesos hidrodinámicos relacionados con la rotura del oleaje en estas condiciones y la formación tanto de corrientes longitudinales como de retorno, fueron cualitativamente bien modelados por el XBeach, comportándose de manera similar a los patrones establecidos en las teorías hidrodinámicas de Gourlay(1974), MacMahan et al. (2004) yMacMahan et al. (2006). Debe destacarse que el modelo permite determinar la formación de socavaciones por efecto de las corrientes, aspecto muy importante a considerar cuando se realiza el diseño estructural de obras de protección costera.

Tercera etapa

Esta etapa tiene como objetivo conocer el desempeño del modelo ante el efecto de la sumergencia de un rompeolas simulando tres cotas de coronación:-0,5 m, 0,00 m y +2,00 m. Para ello se realiza la modelación con entrada del oleaje en dirección 270º utilizando como condición de frontera del oleaje: fondo móvil, Hrms=1m, Trep=7s, duración del evento 200 horas y variación del nivel de marea astronómica.

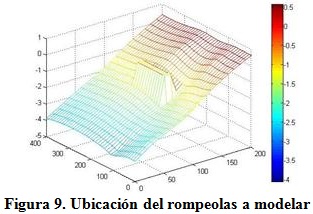
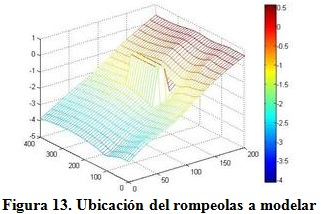
El rompeolas sumergido a modelar presenta una longitud de 120 m, un ancho de 10 m, una cota de -0,5 m por debajo del nivel medio del mar y se ubica dentro de la zona de rompientes en profundidades que oscilan entre 1,5y1,9 m, separado a una distancia de la costa de 60 m como se muestra en la figura 9.

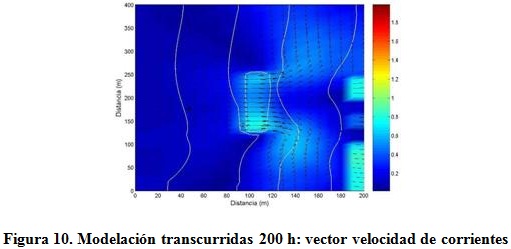
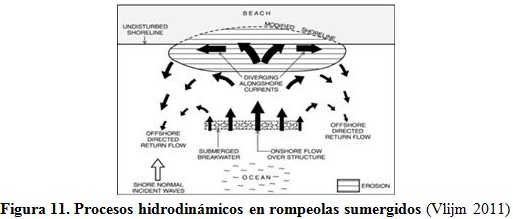
La figura 10 muestra el comportamiento de los vectores de velocidad de las corrientes una vez realizada la modelación, los que responden a la incidencia del oleaje normal a la costa, y donde se observa cómo aumentan sobre el área que ocupa el rompeolas, debido principalmente a la pérdida de energía del oleaje por la rotura y por el proceso de difracción y disipación que provoca la estructura. Para compensar la generación de gradientes por el tensor de radiación, surgen corrientes de retorno, como se muestra en la figura 11 y se describen por Vlijm (2011).

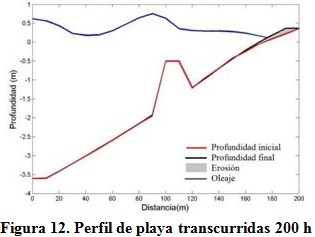
En el perfil longitudinal ubicado en la zona central de la malla de trabajo y que aparece en la figura 12, se observan los niveles de erosión que tienen lugar en la playa con la presencia del rompeolas sumergido al concluir la modelación, lo que coincide con el comportamiento morfológico reportado para este tipo de obras porVlijm (2011).

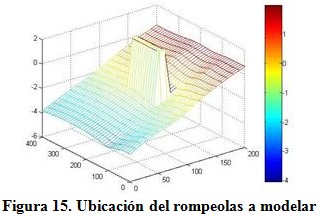
Por su parte el rompeolas sobre el nivel medio del mar a modelar presenta una longitud de 120 m, un ancho de 10 m, una cota de 0,00 m sobre el nivel medio del mar y se ubica dentro de la zona de rompientes en profundidades que oscilan entre 1,5y1,9 m, separado a una distancia de la costa de 60 m como se muestra en la figura 13.

Al concluir la modelación, se observa en la figura 14 (a) que los vectores de velocidad de las corrientes alcanzan sus mayores expresiones sobre el área que ocupa el rompeolas, debido a la rotura del oleaje que se produce por la interacción con la estructura. En la figura 14 (b) se observan los niveles de erosión que tienen lugar en la playa por la presencia del rompeolas, lo que coincide con el comportamiento morfológico reportado para este tipo de obras por Vlijm (2011).

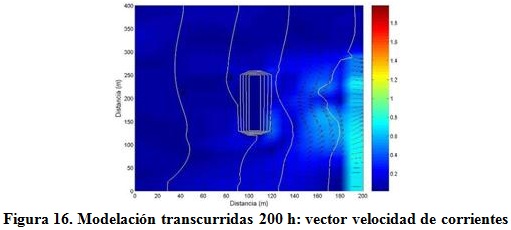
En cuanto al rompeolas emergido a modelar, éste presenta una longitud de 120 m, un ancho de 10 m, una cota de +2,00 m sobre el nivel medio del mar y se ubica dentro de la zona de rompientes en profundidades que oscilan entre 1,5y1,9 m, separado a una distancia de la costa de 60 m como se muestra en la figura 15. En la figura 16 se observa el rompeolas emergido no sobrepasado transcurridas 200 horas de modelación, donde se destacan los patrones de circulación en celdas que se producen en el área a su abrigo y la formación de un saliente en la línea de costa.

El perfil longitudinal ubicado en la zona central de la malla de trabajo, destaca la acumulación de sedimentos que tienen lugar en la playa con la presencia del rompeolas emergido al concluir la

modelación, lo que coincide con el comportamiento morfológico reportado para estas obras en la literatura para el criterio de formación de tómbolos.

Conclusiones de la tercera etapa

Puede concluirse que XBeach es capaz de predecir adecuadamente el efecto de la sumergencia en obras costeras en general, así como el efecto combinado del oleaje y las mareas. Los resultados obtenidos se corresponden con los reportados en la literatura Martínez (2009), Gourlay(1974), Vlijm (2011) entre otros, y deben ser continuados utilizando modelos físicos en laboratorio que permitan su validación.

Cuarta etapa

Durante el desarrollo de esta etapa se simulará la presencia de dos espigones ubicados en los extremos de la zona de estudio y un rompeolas ubicado en la zona central, con el propósito de conocer el desempeño del modelo ante la variedad de obras costeras con diferentes geometrías y funcionamiento. Para ello se realiza la modelación con entrada del oleaje en dirección 270º utilizando como condición de frontera del oleaje: fondo móvil, Hrms=1m, Trep=7s, duración del evento 200 horas y variación del nivel de marea astronómica.

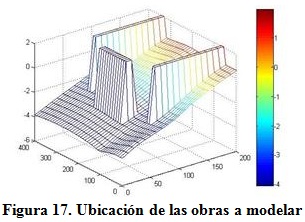
Los espigones a modelar se ubican a 60 m de los límites de la zona de estudio y presentan una longitud de 120 m, un ancho de 10 m, una cota de 2 m por encima del nivel medio del mar alcanzando profundidades entre 2,4 y 2,5 m. Por su parte, el rompeolas posicionado en la zona central presenta una longitud de 120 m, un ancho de 10 m, una cota de 2 m por encima del nivel medio del mar, una separación de 60 m de los espigones y se encuentra en profundidades comprendidas entre 2 y 3 m (figura 17).

La figura 18 (a) refleja el comportamiento de las corrientes longitudinales una vez transcurridas las primeras 50 horas de modelación, donde se destaca la formación de un pequeño saliente que se hace más notable transcurridas 200 horas, como se muestra en la figura 18 (b).

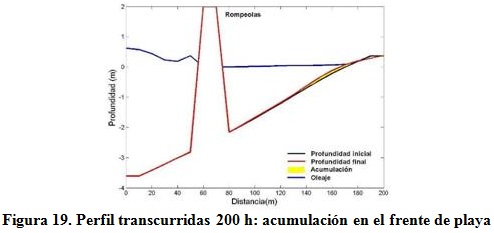
El rompeolas provoca la rotura total del oleaje incidente, sin que se origine transmisión hacia el área que se encuentra bajo su abrigo, propiciando la acumulación de sedimentos y la formación del saliente, lo que se muestra claramente en el perfil longitudinal representado en la figura 19.

Conclusiones de la cuarta etapa

Las modelaciones realizadas en esta etapa permiten concluir que el XBeach es capaz de predecir adecuadamente las condiciones hidrodinámicas y los cambios morfológicos que se presentan ante la variedad de obras costeras como espigones y rompeolas, así como el efecto combinado de la irregularidad del oleaje y las mareas. Estas prestaciones convierten al XBeach en una herramienta de gran utilidad para el diseño de obras de protección costera.Los resultados obtenidos se corresponden con los reportados en la literatura por Gourlay(1974), MacMahanet al. (2004) yMacMahan et al. (2006). Debe realizarse

una verificación de los resultados ya sea mediante el empleo de modelos físicos en laboratorio o mediciones de campo.

Quinta etapa

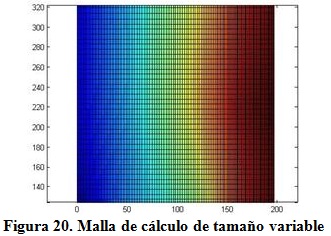
Se modelan las obras descritas en la etapa anterior, aplicando un archivo de código Matlab para la generación de mallas no equidistantes, lo que permite establecer la resolución de la malla de trabajo, así como el tamaño de la malla fijando los valores «dxmáx», «dxmin», «dymáx», «dymin». Este archivo permite introducir los intervalos más finos en la zona de la playa sumergida, la playa seca y las dunas que son las zonas donde ocurren los mayores cambios morfológicos, como muestra la figura 20, donde los máximos intervalos en el sentido de las abscisas dxmáx=3 se encuentran en las mayores profundidades y los intervalos menores dxmin=1 se ubicaron en la playa sumergida, la playa seca y la duna. En cuanto a las ordenadas se establecieron los intervalos dymáx=10 hacia los extremos de la malla y los dymin=5 hacia el centro, donde se ubican las obras a modelar.

Una vez realizada la simulación, se observa que los cambios morfológicos más significativos ocurren a partir de las 50 horas, creándose un saliente que llega a alcanzar sus mayores valores luego de simuladas 200 horas (Perfil transcurridas 200 horas. Acumulación en el frente de playa). En la figura 21 (a) se muestran los cambios ocurridos al transcurrir 200 horas de simulación y el comportamiento de la línea de costa ante la presencia del rompeolas, con la formación de un saliente en el frente de playa que está a su abrigo, lo que se evidencia en el perfil longitudinal de la figura 21 (b). Por otra parte, debido al aumento de la resolución de la malla, se observan con mayor precisión los cambios morfológicos ocurridos en la zona de la playa sumergida y la playa seca.

Conclusiones de la quinta etapa

Las modelaciones realizadas en esta etapa permiten concluir que el XBeach es capaz de predecir adecuadamente las condiciones hidrodinámicas y los cambios morfológicos que se presentan ante la variedad de obras costeras como espigones y rompeolas, así como el efecto combinado del oleaje y las mareas. La aplicación de mallas no equidistantes permite refinar el área de interés, proporcionar un resultado de mayor precisión, así como optimizar el número de nodos.

CONCLUSIONES

Las modelaciones realizadas en 2D muestran que el modelo matemático es capaz de predecir los cambios morfológicos en las playas ante la presencia de obras costeras como espigones y rompeolas, bajo el efecto combinado de la irregularidad del oleaje y las mareas, simulando adecuadamente el comportamiento hidrodinámico de estas obras. Se recomienda continuar profundizando en la aplicación y establecimiento de este modelo matemático por sus amplias posibilidades en la reproducción de los fenómenos que se desarrollan en la interacción oleaje estructuras costeras.

 

 

REFERENCIAS BIBLIOGRÁFICAS

Cabrera A. H., Sáez D. M., Santos O.R. y Cruz T.S. «Manejo costero integrado y política pública en Iberoamérica: Propuestas para la acción». Servicio de Publicaciones del Programa Iberoamericano de Ciencia y Tecnología para el Desarrollo.Red IBERMAR (CYTED), pp. 71-91, Cádiz, España. (2011).

Córdova L. y Valdés K. «Control de erosión en tramo costero de Varadero aplicando soluciones combinadas». Ingeniería Hidráulica y Ambiental, (2011), vol. 32, no. 3, pp. 64-71, CIH, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana.

Córdova L. «Sistema de ingeniería de costas: evaluación del proceso de erosión en la playa Varadero». Ingeniería Hidráulica y Ambiental, (2014), vol 35, no. 3, pp. 17-31, CIH, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana.

EIRD «Estrategia Internacional para la Reducción de los Desastres. Vivir con el riesgo, énfasis en la reducción del riesgo de desastres». Naciones Unidas, Ginebra, Suiza. (2003).

Gourlay M. R. «Wave set-up and wave generated currents in the lee of a breakwater or headland». Proceedings 14^thCoastal Engineering Conference, Copenhagen, Denmark. American Society of Civil Engineers ASCE, (1974), vol.3, pp. 19761987, New York, United States of America.

MacMahan J. H., Reniers H.M, Thornton E. B and Stanton T.P. «Surf zone eddies coupled with rip current morphology». Journal of Geophysical Research: Oceans, (2004), vol. 109, issue C7. American Geophysical Union, United States of America.

MacMahan J.H., Thornton E.B. andReniers H.M. «Rip current review».Coastal Engineering Journal, (2006), vol. 53,issue (23), pp.191208, United States of America.

Martínez P. A. «Modelado de la evolución de la línea de costa tras diques exentos de baja cota de coronación». Escuela Técnica Superior de Caminos, Canales y Puertos. Universidad Politécnica de Cataluña, Barcelona, España. (2009).

Pattiaratchi C., Olsson D., Hetzel Y. and Lowe R. «Wave driven circulation patterns in the lee of groins». Continental Shelf Research Journal, (2009), vol. 19, issue 16, pp.1961-1974. University of Western Australia, Australia.

Roelvink D., Reniers A., vanThiel de Vries J. andMcCall R. «XBeach Model Description and Manual».Unesco-IHE Institute for Water Education, Deltares and Delft University of Technology, The Netherlands. (2010).

Vlijm R. J. «Process-based modelling of morphological response to submerged breakwaters». Master of Science Thesis in Coastal Engineering. Delft University of Technology, The Netherlands. (2011).

 

 

Recibido: 4 de enero de 2015.
Aprobado: 30 de abril de 2015.

 

 

Kenia Hernández Valdés, Luis F. Córdova López. Inversiones Gamma S.A. Playa. La Habana, Cuba. Centro de Investigaciones Hidráulicas. Instituto Superior Politécnico José Antonio Echeverría (Cujae). La Habana. Email:[e-mail], email:[e-mail]