Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Hidráulica y Ambiental
versión impresa ISSN 1680-0338
riha vol.38 no.1 La Habana ene.-abr. 2017
ARTÍCULO ORIGINAL
Modelación hidráulica de humedales artificiales de flujo sub-superficial horizontal
Hydraulic modelling for horizontal subsurface flow constructed wetlands
Josué Bernardo Larriva Vásquez,I Orestes Arsenio González Díaz,II
I ETAPA EP, Empresa de telecomunicaciones, agua potable y saneamiento de Cuenca, Ecuador.
II Centro de Investigaciones Hidráulicas (CIH). Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana.
RESUMEN
En el presente trabajo se presentan los estudios realizados mediante pruebas de trazadores para caracterizar el comportamiento hidráulico de un humedal con flujo sub-superficial horizontal para el tratamiento de aguas residuales. La aplicación de diferentes modelos para el estudio del flujo dentro del reactor mostró la importancia de incorporar en las metodologías de diseño los elementos geométricos e hidráulicos que aseguren el comportamiento del flujo a esperar y por tanto las eficiencias en la remoción de contaminantes.
Palabras clave: comportamiento hidrodinámico, humedales artificiales, modelos de flujo, modelo de tanques en serie, modelo de Wolf-Resnick.
ABSTRACT
In the present work studies are presented using tracer tests to characterize the hydraulic behavior of a constructed wetland with horizontal subsurface flow for wastewater treatment. The application of different models for the study of flow inside the reactor showed the importance of including geometric and hydraulic elements in the design methodology in order to assure the expected flow behavior and therefore contaminant removing efficiency.
Key words: hydrodynamic behavior, artificial wetlands, flow models, series tank model, Wolf-Resnick model.
INTRODUCCIÓN
Los tratamientos llamados no convencionales o tecnologías blandas se muestran como una alternativa para el tratamiento de las aguas residuales para comunidades pequeñas o sistemas rurales, ya que no son costosos ni requieren altos consumos energéticos, además la operación y mantenimiento de estos no requieren de personal especializado ni procesos complicados.
A nivel mundial se ha extendido cada vez más el uso de los humedales artificiales o wetlands, los cuales funcionan a partir de los mecanismos propios que usa la naturaleza para la depuración de las aguas residuales, donde se combinan procesos físicos, químicos y biológicos entre el suelo, las plantas, los microorganismos y la atmósfera. Existen 2 tipos de humedales artificiales, de acuerdo con el tipo de flujo: los de flujo superficial, en los que el agua fluye expuesta a la atmósfera, y los conocidos como de flujo sub-superficial, en donde el agua fluye a través de un material de soporte, generalmente grava. Estudios publicados demuestran la capacidad de los humedales de flujo horizontal sub-superficial para remover cantidades significativas de materia orgánica, nitrógeno, fósforo, sólidos suspendidos, bacterias y metales pesados del agua residual (González 2011).
El presente trabajo se realiza como parte de los estudios de tratabilidad mediante humedales de flujo sub-superficial para las condiciones de los sistemas rurales ubicados en los Andes Ecuatorianos de la provincia del Azuay en donde las poblaciones se asientan sobre los 2500 m.s.n.m. El clima durante el año va de templado a frío y el sistema de alcantarillado cuenta con cargas orgánicas bajas debido a la dilución que ocurre por la introducción de agua de origen pluvial en los sistemas sanitarios. Estas condiciones conducen a esperar eficiencias menores en la remoción de contaminantes, sabiendo que la adaptación de cualquier tecnología a las condiciones propias de un lugar requiere de estudios o valoraciones previas que conduzcan a la obtención de coeficientes propios de diseño o adaptaciones a la metodología de diseño utilizada en lugares en donde estos procesos ya han sido estudiados.
El objetivo de los estudios realizados es caracterizar el tipo de flujo en los humedales sub-superficiales, a partir de pruebas de trazadores y basado en la aplicación de expresiones conocidas de otros sistemas de tratamiento biológicos. Tradicionalmente el diseño de los sistemas de tratamiento de aguas residuales se han centrado en modelos biológicos dejando en un segundo plano los aspectos hidráulicos como las relaciones geométricas, características del flujo, tiempos de retención hidráulico, tipo de mezcla, etc., los cuales influyen en las eficiencias que puedan lograrse en el proceso biológico que ocurre en cada tipo de reactor.
Sin embargo trabajos recientes como los presentados por González (2011), aplicado a humedales de flujo sub-superficial o los de Rocha et al. (2000) y más recientemente Pérez y Torres (2008) aplicado a reactores anaerobios de crecimiento en medio fijo con flujo horizontal muestran la importancia de incluir los criterios hidráulicos dentro de la valoración del funcionamiento del reactor con el objetivo de asegurar las remociones esperadas de los distintos contaminantes biológicos.
MODELOS HIDRÁULICOS APLICABLES AL FLUJO SUB-SUPERFICIAL EN HUMEDALES ARTIFICIALES
Modelación matemática del fenómeno de dispersión del flujo sub-superficial
El primero en proponer el empleo de la distribución del tiempo de residencia (RTD) para caracterizar los reactores químicos fue Danckwertsen en 1953 (Kadlec and Wallace 2009). Para lograr la predicción del comportamiento del flujo dentro de un reactor es imprescindible el conocimiento de la curva de distribución de tiempos de residencia (RTD) de la corriente del fluido. Esta información puede determinarse mediante el método experimental estímulo-respuesta, el cual consiste en introducir una perturbación en el flujo (inyección de trazador) y observar su comportamiento a lo largo del tiempo (la distribución de las concentraciones) (Levenspiel 1997).
La correcta formulación de los fenómenos de dispersión y difusión es compleja ya que es difícil simular física y matemáticamente los fenómenos que tienen lugar en el flujo a través de un medio poroso, aun en casos sencillos.
Módulos de dispersión en sistemas de tratamiento naturales
Entre los sistemas de tratamiento un parámetro de especial importancia es la determinación del módulo de dispersión. Tanto en las lagunas como en los humedales artificiales, es importante la ocurrencia de flujo lo más pistón posible y la no existencia de zonas muertas ni de cortocircuitos. En el análisis realizado por González (2014) se muestra que el módulo de dispersión en un reactor podía relacionarse con algunos factores de la forma geométrica y con las propiedades del fluido y se cita como una ecuación adaptada de la expresión propuesta por Liu en 1977 es aplicable a reactores estrechos, teniendo en cuenta la profundidad del reactor independiente del radio hidráulico, según ecuación (1).
![]()
En la que: W es el ancho del reactor, L es la longitud del reactor, h es la profundidad del reactor y α es una constante que depende sólo de la forma de la sección transversal del canal y de la forma de distribución de la velocidad, pero no de su tamaño o de la magnitud de la velocidad de la corriente, u es la velocidad media del flujo en el reactor (m/d) y u* es la velocidad cortante o dinámica que depende del número de Reynolds.
D/vL es un grupo adimensional denominado módulo de dispersión del recipiente y mide el grado de dispersión axial. Por lo tanto, si:
D/vL tiende a cero (Dispersión despreciable) se tiende a flujo pistón.
D/vL tiende al infinito (Dispersión grande) se tiende a mezcla completa.
El módulo de dispersión mostrado anteriormente expresado como su inverso, se denomina número de Peclet. Este modelo es muy eficaz cuando el flujo no se desvía demasiado del flujo pistón, como pasa en medios porosos (Levenspiel 1997).
Modelo de tanques en serie
En el caso ideal de que exista un reactor de mezcla completa perfecta y se le inyecte en forma de disparo un trazador conservativo, el mismo se mezcla instantáneamente y comienza a aparecer en la salida con un comportamiento respecto al tiempo similar al de una curva exponencial de exponente negativo, ya que en el instante t=0 aparece la concentración inicial instantánea y paulatinamente se va diluyendo con el flujo que continúa entrando al reactor. La ecuación (2) describe dicha distribución de concentraciones respecto al tiempo.
![]()
En la cual C0 es la concentración inicial de trazador, C la concentración de salida, t0 el tiempo de retención teórico, Q el gasto de entrada y V es el volumen del reactor.
Si se colocan dos reactores de mezcla completa de iguales dimensiones uno a continuación del otro y se efectúa una inyección de trazador en forma de disparo en el primer reactor, entonces la concentración de entrada del segundo sería la concentración de salida del primero, cuya ecuación de concentración de salida sería la ecuación (3).
![]()
Donde V es el volumen total de todos los reactores y V/N es el volumen de un reactor. Planteando un balance de masa para el segundo reactor, sustituyendo la concentración de entrada de éste por la de salida del primero y resolviendo la ecuación diferencial aplicando integral de convolución o la Transformada de Laplace, se llega a la ecuación (4).
![]()
Y para describir el comportamiento de la concentración del efluente en el i-ésimo reactor queda la forma generalizada en la ecuación (5).
![]()
Crites and Tchobanoglous (1998) obtuvieron las curvas del efluente para uno, dos, cuatro, seis y 75 reactores en serie y notaron que un modelo que incluye entre cuatro y seis reactores de mezcla completa en serie puede ser usado para describir las características hidráulicas de los humedales artificiales. De esta forma, a partir de las curvas de concentración de trazador contra tiempo obtenidas experimentalmente en un reactor cualquiera, puede determinarse el número de tanques de mezcla completa que lo caracterizan, o sea, que tienen la misma RTD que el reactor en cuestión. El modelo de tanques en serie supone que el reactor puede representarse dividido en varios tanques de mezcla completa ideal, del mismo tamaño, en serie, siendo la cantidad de tanques el único parámetro a determinar (Levenspiel 1997). Para este modelo no se presentan los problemas de fijar las condiciones de contorno, ni los modos de inyectar y medir el trazador, por lo que las curvas C o E pueden obtenerse fácilmente. Así, para un solo tanque (mezcla completa) se obtiene la ecuación (6).
![]()
Y para N tanques en serie la ecuación (7):
![]()
Siendo t-: tiempo medio de residencia por cada tanque; t-= Nt-i tiempo medio de residencia en el conjunto de N tanques; θi = t / t-i= N t / t- y θ = t / t- = t / Nt-i.
Las expresiones planteadas por Crites and Tchobanoglous (1998), son similares a las planteadas por Levenspiel (1997), sólo que estas últimas se presentan de forma normalizada. Obsérvese que, lógicamente, mientras mayor es N más se acerca el comportamiento al flujo pistón. El valor del parámetro N puede calcularse mediante la varianza de la curva C (Kadlec and Wallace 2009) o mediante determinación del punto de máximo de la misma (Levenspiel 1997).
Modelo de tanques en serie con retardo
Para ajustar el modelo de tanques en serie a las características de los humedales de flujo subsuperficial se debe analizar el tiempo que tarda la respuesta del trazador aplicado en alcanzar la salida del lecho. Tal retardo se puede describir mediante la adición de un elemento de flujo pistón de la red de flujo (Kadlec and Wallace 2009), denominando td al tiempo de retardo puede plantearse la RTD en dos partes, ecuaciones (8) y (9).
![]()
![]()
Aquí puede observarse que lo planteado en la ecuación anterior es sólo el desplazamiento del intercepto en el modelo de tanques en serie para hacerlo coincidir con los datos reales observados en un humedal.
Otros modelos para valorar la dispersión en 1 dimensión, como el Método de los Elementos Finitos con elementos cuadráticos, usado por Marón (2001), muestran que existe una buena aproximación entre los resultados obtenidos de la aplicación del método de Tanques en Serie con Retardo aplicado por González (2014) en pruebas realizadas desde el año 2000 y el de las diferencias finitas, lo cual demuestra la validez de aplicar este modelo en el presente trabajo para el cálculo del módulo de dispersión en SFS.
Método de Wolf y Resnick
Estos investigadores (CEPIS 2004) han propuesto un método que analiza la totalidad de la curva de concentración contra tiempo y no solo las tendencias centrales. Si se tabula la curva tiempo concentración y si denominamos F(t) a la fracción de volumen que sale del reactor antes del tiempo de retención teórico t0, la ecuación de la misma es la ecuación (10).
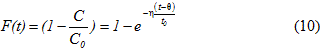
En la que se asocia la ecuación (11).
![]()
Donde p es la fracción de flujo considerado como pistón, m es la fracción del volumen considerado muerto, θ es el desplazamiento de la curva debido a espacios muertos y la ecuación (12).
![]()
Caracteriza a la eficiencia de la mezcla. Estos valores pueden ser calculados por métodos gráficos, dibujando a escala semi logarítmica la curva 1 F(t), a partir del ángulo α y el valor de θ, que se muestran en la figura 1.
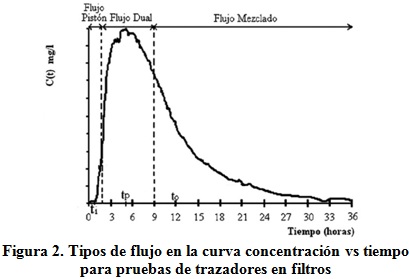
Análisis de la curva RTD del CEPIS
Adicionalmente al método de Wolf-Resnik en la documentación técnica generada por el Centro Panamericano de Ingeniería Sanitaria y Ambiental (CEPIS 2004) se presenta un análisis de la curva RTD para el índice de morbilidad de coliformes totales en filtros, que si bien son otro tipo de reactores, sirve para obtener valores cualitativos del tipo de flujo que se presenta analizando los diferentes tiempos en que se producen las concentraciones iniciales, máximas y finales del trazador utilizado, y en función de estos valores se caracteriza al reactor.
De acuerdo con este organismo al analizar la forma de la curva RTD se pueden identificar 3 zonas importantes, las cuales se pueden ver en la figura 2. En el documento se citan los estudios realizados por Hirsh, quien indica que la fracción de flujo pistón puede considerarse hasta el primer punto de inflexión de la curva en donde cambia de concavidad. Entre este punto y el punto de inflexión de la rama descendente de la curva se considera un flujo dual, entre pistón y mezclado y a partir de este último punto es predominantemente mezclado.
En la metodología de análisis propuesta se definen varias relaciones entre los tiempos de ocurrencia de las distintas concentraciones del trazador en el reactor, así como la excentricidad de la curva RTD, para caracterizar la tendencia hacia el flujo pistón o mezcla completa, de entre las cuales se utilizarán las correspondientes a los siguientes tiempos:
to: tiempo teórico de retención
tp: tiempo modal, correspondiente a la presentación de la máxima concentración
ti: tiempo de aparición del trazador
tf: tiempo para que atraviese la totalidad del trazador
En función de estos valores puede evaluarse las siguientes relaciones:
tp/to ≈ 1 y tp/to 0.5 predominio del flujo pistón
ti/to = 0 mezcla completa, ti/to = 1 flujo pistón y ti/to< 0,3 presencia de cortocircuitos
Y se define la excentricidad e de la curva con la ecuación (13).
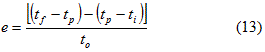
Para la cual los valores mayores que 2,3 mostrarían un flujo de mezcla completa, y un valor de excentricidad igual a cero representaría el flujo pistón teórico.
MATERIALES Y METODOS
Para el desarrollo de este trabajo se utilizaron las instalaciones de la planta de tratamiento de aguas residuales de Ucubamba pertenecientes a la Empresa Municipal de Telecomunicaciones, Agua Potable y Saneamiento de la ciudad de Cuenca ETAPA EP, ubicando los pilotos junto a la salida del desarenador de la planta desde donde se alimenta a los mismos.
Se utilizaron tres reactores (tanques de acero inoxidable) de sección transversal trapezoidal de 2,8 m de largo, 0,6 m de profundidad, 1,3 m de ancho superior y 1,2 m de ancho inferior como se muestra en la figura 3. Como material de soporte se utilizó grava de 18 a 25 mm, con una porosidad del 38%. Su colocación fue aleatoria ocupando un volumen efectivo de aproximadamente 0,6 m3.
Los pozos de muestreo están colocados de forma vertical, desde el fondo del reactor hasta 5 cm por encima de la grava, en el medio soporte. Consisten en 4 tubos de 150 mm de diámetro y 0,65 m de longitud perforados en toda su área lateral para permitir que el flujo pase a través de ellos sin que se originen perturbaciones. Están espaciados a 1,00 m y separados 0,90 m de la entrada y salida en sentido longitudinal, con el objetivo de obtener mediciones por tercios del reactor y sobre la misma prueba obtener varios resultados. Los pozos están espaciados a 0,60 m y separados 0,40 m de los laterales en la parte superior del reactor en sentido transversal, con el fin de evitar la influencia de las condiciones de contorno.
Los reactores fueron diseñados considerando una pendiente de 1% (EPA 2000) para garantizar un gradiente hidráulico. Como estructura de entrada se colocó piedra de 18 a 25 cm de diámetro para evitar obstrucciones en el sistema y sobre esta zona se colocó un tubo de PVC de 25 mm de diámetro perforado con 10 agujeros de 9 mm de diámetro a cada lado. Adicionalmente como estructura de entrada se colocó un baffle de acero inoxidable en los 30 cm superiores del área de entrada lo que obliga a que el agua salga por la parte inferior y así minimizar las zonas muertas.
Para recoger el agua se utilizó otro tubo de PVC de 50 mm de diámetro perforado con 10 agujeros de 9 mm de diámetro, precedido así mismo de otro bafle de acero inoxidable mediante el cual se asegura la utilización de todo el volumen del reactor. En la figura 4 se pueden observar las estructuras de entrada y salida. El efluente de los tres reactores se vierte hacia el drenaje de la planta de tratamiento.
Para las pruebas de trazadores se utilizó sal, realizándose medidas indirectas de la concentración a través del valor de la conductividad presente en el agua. Para la medición de la conductividad se fabricaron tres dispositivos con un microprocesador capaz de guardar en memoria los datos obtenidos y ser programado para diferentes tiempos de lecturas, estos dispositivos fueron calibrados mediante soluciones con concentraciones de sal conocidas preparadas en el laboratorio como puede observarse en la figura 5, al igual que la disposición de los mismos para la toma de muestras en los pozos de muestreo ubicados en los reactores. Debido a que solamente se contó con tres equipos de medición fue necesario realizar varias pruebas para un mismo tiempo de retención, utilizando alternadamente los equipos en los diferentes pozos de muestreo.
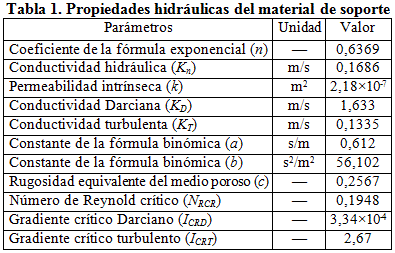
Para el material de soporte se realizaron las pruebas de granulometría, peso específico, porosidad y para la obtención de la conductividad se construyó un permeámetro, el cual se muestra en la figura 6, al cual se le aplicaron 6 gastos diferentes para los que se registraron los valores de carga piezométrica en 3 puntos a lo largo del dispositivo.
Con las lecturas obtenidas se tabularon los datos y se calcularon los coeficientes de la fórmula exponencial, los de la ecuación binómica de Forchheimer, además de los distintos valores de la conductividad, permeabilidad intrínseca, y demás propiedades hidráulicas del material, las cuales se muestran en la tabla 1:
RESULTADOS Y DISCUSIÓN
Se realizaron 35 pruebas entre enero y febrero del 2014 para tiempos de retención hidráulico de 24 y 36 horas, en las que se tomaron los valores de conductividad alternadamente entre los pozos de muestreo ubicados en el primero y segundo tercio del reactor y en la salida del mismo. Las curvas de trazadores que se muestran en la figura 7 corresponden a las pruebas con mejor calidad de datos de los ensayos realizados.
En la figura se pueden observar las RTD para 24 y 36 horas de tiempo de retención en los pozos ubicados en los primeros tercios, así como en los segundos tercios y la salida tiene un comportamiento similar entre los pozos ubicados a la misma distancia longitudinal y para los dos tiempos estudiados, lo anterior permite hablar de un comportamiento de la velocidad bastante constante y de la dispersión bastante baja, referido al ancho del reactor, observándose que mientras mayor es la distancia con respecto a la entrada las curvas obtenidas son más uniformes, lo que indica que mientras menor sea la velocidad promedio de circulación del humedal, es decir, mientras mayor sea el tiempo de retención, menor será la diferencia de velocidad y dispersión a lo largo de los ejes y y z y por ende, aumentará la tendencia a pistón del flujo.
Para la aplicación del modelo de dispersión axial en el reactor se procedió a normalizar las curvas de concentración vs. tiempo con el fin de calcular la varianza adimensional al cuadrado, y en función de este el índice o módulo de dispersión obteniéndose los valores que se muestran en la tabla 2 para los diferentes pozos de muestreo, incluyéndose en la tabla también las relaciones largo ancho correspondientes a cada pozo.
Si se comparan los resultados obtenidos con los expuestos en la figura 1 se puede observar que para los pozos de muestreo ubicados en el primer tercio del reactor el módulo de dispersión obtenido puede considerarse grande por ser mayor que 0,20, sin embargo, conforme aumenta la relación largo ancho el valor disminuye a valores entre grande e intermedio.
No obstante, para poder reproducir de manera adecuada el funcionamiento del humedal de flujo sub-superficial, se aplicó el modelo de tanques en serie con retardo, procediéndose a calcular el número de tanques en serie característico (que es el inverso de la varianza adimensional) y el tiempo de retardo teórico. Adicionalmente se procedió a comparar las curvas adimensionales obtenidas, con las curvas calculadas para el número entero de tanques en serie más cercano al valor calculado. Las figuras 8 y 9 muestran los gráficos de las curvas anteriormente descritas y la tabla 3 los valores obtenidos.
Como se puede observar los resultados obtenidos muestran que este método es el de mejor ajuste al funcionamiento real de los humedales de flujo sub-superficial horizontal, ya que las curvas observadas vs. las calculadas muestran grandes similitudes para los 2 tiempos de retención estudiados, además de que la diferencia entre el tiempo de retención hidráulico y el real son muy similares al retardo calculado por este método, como por ejemplo para el segundo tercio del reactor para el TRH de 24 horas se calcula un valor de 0,217 y se obtienen valores de 0,218 y 0,198. Si se analizan los demás resultados se puede concluir que todos tienen un orden de magnitud semejante. Por otro lado se puede observar la forma y esbeltez de las curvas observadas, las cuales para una relación largo/ancho de 0,75 pasan de mostrar una gran tendencia del flujo a la mezcla completa hasta las del reactor completo, cuyas curvas se vuelven más simétricas, lo que indica la tendencia hacia el flujo a pistón. Los resultados obtenidos permiten concluir que el modelo de tanques en serie con retardo reproduce de forma adecuada los valores de Cq obtenidos experimentalmente. Adicionalmente se puede ver que conforme aumenta la relación largo/ancho aumenta el número de tanques en serie, con lo cual aumenta también la tendencia al flujo pistón dentro del reactor.
Análisis por el método de Wolf-Resnick
De lo descrito en la introducción el método de Wolf-Resnick permite la determinación de características importantes del flujo dentro del reactor: el % de zonas muertas y % de flujo pistón, y por tanto el % de flujo perfectamente mezclado. Por tal razón se aplicó a los datos obtenidos en el modelo físico en estudio con la intención de comparar estos resultados con los criterios cualitativos sobre las características del flujo obtenidos a partir de la observación de las RTD de cada uno de los pozos. Para su aplicación se tomaron en cuenta únicamente los primeros valores de las series, se trazó una curva de tendencia en escala semi logarítmica y se trazó la tangente con el fin de poder evaluar los valores de α y θ para las curvas anteriormente mostradas. Las curvas para los pozos ubicados en cada tercio y la salida del reactor, así como los resultados numéricos obtenidos para todos los pozos de muestreo en los dos tiempos de retención analizados se muestran en las figuras 10 y 11 y la Tabla 4.
Como se puede observar los resultados obtenidos son coherentes con los resultados del modelo de tanques en serie con retardo, y muestran cómo, al ir aumentando la relación largo ancho, aumenta la tendencia al flujo pistón, que para el caso del total del reactor es del orden del 86%.
También se puede ver cómo los resultados para los dos tiempos de retención son similares, sin embargo para el TRH de 36 horas disminuye el porcentaje de zonas muertas, por lo que para tiempos de retención mayores, del orden de 2 a 3 días, necesarios para la remoción de DBO se puede esperar que se mantengan o mejoren estas condiciones de flujo. Además este método permite determinar el % de zonas muertas, el cual como se puede ver, disminuye conforme va aumentando la relación largo/ancho, lo cual es muy importante pues muestra la ocurrencia de un flujo bastante provechoso para la depuración del agua residual.
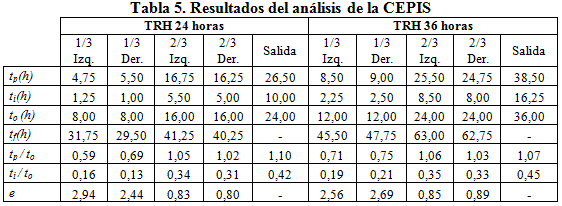
Análisis por el método del CEPIS
Finalmente se practicó el análisis descrito por el CEPIS para los tiempos obtenidos en las curvas RTD, y que serviría para corroborar los valores obtenidos por el método de Wolf-Resnick. Los valores obtenidos de este análisis se muestran en la tabla 5.
Como se puede observar los resultados obtenidos llevan a conclusiones similares de manera cualitativa a las mostradas con la aplicación del método de Wolf-Resnik. En el caso de la relación tp/to se puede observar que, a partir del segundo tercio del reactor, el valor es semejante a 1, lo que indica el predominio del flujo pistón, cosa que se puede concluir también si se analiza la excentricidad, cuyo valor es muy fuerte en el primer tercio del reactor y que disminuye considerablemente a partir del segundo tercio. En el caso de cortocircuitos o zonas muertas, si ¡comparamos los valores de la relación ti/to con 0,3, se puede observar como para el primer tercio este valor es mucho menor, indicativo de cortocircuitos y a partir del segundo tercio estos prácticamente desaparecerían, lo cual concuerda con el porcentaje de zonas muertas calculado por el método de Wolf-Resnick. Al igual que en las conclusiones de dicho método ahora también se puede decir que los resultados entre ambos tiempos de retención son muy similares, por lo que se puede esperar que se mantenga este comportamiento para los tiempos de retención a emplear para la depuración biológica.
CONCLUSIONES
Se demuestra, mediante el uso de trazadores y la aplicación de varios modelos para valorar el funcionamiento hidráulico, que el modelo de tanques en serie con retardo es el que mejor representa las condiciones de flujo en los humedales con flujo sub-superficial horizontal. De la experiencia realizada se puede concluir, mediante el uso de varias metodologías, que escoger adecuadamente las relaciones geométricas en este tipo de reactores asegura la tendencia en el comportamiento del flujo y disminuye la presencia de zonas muertas o cortocircuitos. En los resultados obtenidos en el presente trabajo se puede observar que para los tiempos de retención hidráulicos ensayados una relación largo/ancho 2:1 a 3:1 se podría considerar suficiente para asegurar la tendencia hacia flujo pistón en humedales artificiales de flujo sub-superficial horizontal, con lo cual se mejora la eficiencia en la remoción de contaminantes, y que para otros tiempos de retención deben buscarse relaciones geométricas adecuadas que aseguren dichas eficiencias.
REFERENCIAS BIBLIOGRÁFICAS
1. CEPIS «Tratamiento de agua para consumo humano. Filtración rápida». Centro Panamericano de Ingeniería Sanitaria y Ambiental. Perú. (2004)
2. Crites R. and Tchobanoglous G. «Small and decentralized wastewater management systems». McGraw-Hill Editorial, ISBN 978-0072890877, New York. (1998)
3. EPA «Constructed wetlands treatment of municipal wastewater». U.S. Enviromental Protection Agency, Office of Research and Development, EPA/625/R-99/010, Cincinnati, Ohio, USA. (2000).
4. González O. «Metodología para el diseño de humedales de flujo sub-superficial» Ingeniería Hidráulica y Ambiental, (2011), vol 32, no. 1, pp 61-70, ISSN 1815-591X, Centro de Investigaciones Hidráulicas (CIH). Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana.
5. González O. «Modelación matemática del fenómeno de la dispersión en humedales de flujo sub-superficial horizontal». 17 Convención Científica de Ingeniería y Arquitectura, Habana. Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana. (2014)
6. Kadlec R. H. and Wallace S. «Treatment Wetlands». Taylor & Francis Group, ISBN 978-1-56670-526-4, Boca Raton, Florida, USA. (2009).
7. Levenspiel O. «Ingeniería de las reacciones químicas». Editorial Reverté S.A., Sexta edición, ISBN 64291-73250, Barcelona, España. (1997)
2. Marón D. D. «Aplicación del Método de los Elementos Finitos (MEF) y del Método de las Diferencias Finitas (MDF) en modelos de flujo y de transporte de contaminantes con densidad constante o variable en medios porosos saturados», Tesis de doctorado en Ciencias Técnicas, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Cuba. (2001)
8. Perez A. y Torres P. «Evaluación del comportamento hidrodinâmico como herramienta para optimización de reactores anaeróbios de crecimiento en medio fijo». Revista Facultad de Ingeniería de la Universidad Antioquia, (2008), No. 45, pp. 27-40, ISSN 0120-6230, Colombia.
9. Rocha M. A., Normando H. y Onofre C. «Aplicao de tracadores em filtros anaeróbicos para avaliacao das características hidrodinamicas». XXVII Congresso Interamericano de Engenharia Sanitária e Ambiental, Associacao Brasileira de Engenharia Sanitária e Ambiental, Porto Alegre, Brasil. (2000)
Recibido: 5 de junio de 2015.
Aprobado: 25 de octubre de 2016.
Josué Bernardo Larriva Vásquez, Orestes Arsenio González Díaz. ETAPA EP, Empresa de telecomunicaciones, agua potable y saneamiento de Cuenca, Ecuador. Centro de Investigaciones Hidráulicas (CIH). Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana. e-mail: jlarriva@etapa.net.ec, e-mail: orestes@cih.cujae.edu.cu