Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Hidráulica y Ambiental
versión impresa ISSN 1680-0338
riha vol.38 no.1 La Habana ene.-abr. 2017
ARTÍCULO ORIGINAL
Modelo numérico de intrusión salina con dispersión hidrodinámica
Numerical model of saline intrusion with hydrodynamic dispersion
Dr. David Ernesto Marón Domínguez,I Ing. Odet Caridad Herrera Betancourt,II Ing. Ysnayan Fernández Legón,III Ing. Lemuel Carlos Ramos Arzola,IV Dr. Armando Orestes Hernández Valdés,IV
I Centro de Estudios Matemáticos, Univ. Tecn. de La Habana José Antonio Echeverría (Cujae).
II Grupo Empresarial Investig., Proy. e Ing, Inst. Nac. Recursos Hidráulicos (INRH), Habana.
III Empresa Aguas de la Habana, Habana, Cuba.
IV Centro de Investig. Hidráulicas, Univ. Tecn. de La Habana José Antonio Echeverría (Cujae).
RESUMEN
Se presenta un modelo numérico de intrusión salina con dispersión hidrodinámica, por lo que se considera la densidad del fluido como variable en función de la concentración de sal. El modelo matemático está formado por la ecuación de flujo y la ecuación del agua salada en el plano vertical. Se aplica el Método de los Elementos Finitos con triángulo lineal para la discretización en el espacio, y el Método de las Diferencias Finitas para la discretización en el tiempo. Se comprueba el algoritmo de cálculo, utilizado en el modelo, con ejemplos reportados en la literatura obteniéndose buen ajuste en cuanto a los resultados de las curvas de nivel de las cargas y de las concentraciones.
Palabras clave: dispersión hidrodinámica, intrusión salina, método de los elementos finitos, modelo matemático.
ABSTRACT
A numerical model of saline intrusion is presented with hydrodynamic dispersion, meaning that the fluid density is considered as a variable as a function of the salt concentration. The mathematical model is formed by the flow equation and the saltwater equation in the vertical plane. The Method of Finite Elements is applied with linear triangles in the space domain and the Method of Finite Differences in the time domain. The calculation algorithm used in the model is tested against examples reported in the literature. The results show a good adjustment for the contour lines of water levels and salt concentrations.
Key words: hydrodynamic dispersion, seawater intrusion, finite element method, mathematical model.
INTRODUCCIÓN
Uno de los principales problemas de contaminación de las aguas subterráneas en el mundo, y en particular en Cuba, es la intrusión salina. Los primeros estudios realizados en la modelación de este problema suponen que la intrusión salina en el acuífero está en equilibrio estático, que no hay superficie de filtración ni de escape, y que el agua dulce se separa del agua de mar por una interfaz abrupta bien definida con forma recta sin que exista mezcla entre los dos fluidos. Posterior a estos estudios, Hubbert (1940) demostró que la continuidad de la presión en el fluido podía mantenerse a través de la interfaz. Este autor considera el equilibrio dinámico para la interfaz, para la superficie de filtración y para la superficie de escape. La interfaz puede ser tratada como una superficie frontera bien definida y con forma curva que acopla los dos campos de flujos separados. Para este caso la profundidad z de la interfaz es la dada por ecuación (1).
![]()
Donde: ρd = 1000 kg/m3 es la densidad del agua dulce, ρs = 1025 kg/m3 es la densidad del agua salada, z es la profundidad medida positiva desde el nivel medio del mar hasta la interfaz para un punto a una distancia de la costa (m), hd es la carga de agua dulce por encima del nivel medio del mar en el mismo punto (m) y hs es la carga de agua salada medida desde el nivel medio del mar en el mismo punto (m).
En realidad el agua de mar se mezcla con el agua dulce formándose una zona donde predomina la dispersión o la difusión hidrodinámica. En algunos acuíferos donde la franja de dispersión no es tan ancha el modelo de la interfaz abrupta es una primera aproximación, aunque no puede describir totalmente la naturaleza de la intrusión salina. Cuando la zona de transición es ancha es necesario resolver un problema de una fase de fluido con un soluto resolviendo simultáneamente la ecuación de flujo y la ecuación de la adveccióndispersión. En el modelo con dispersión hidrodinámica, la densidad varía con la concentración de la sal y se tiene que trabajar con una ecuación de estado que relaciona la densidad en función de la concentración.
Pinder y Gray (1977) obtuvieron una solución del estado impermanente para el problema de la intrusión de agua salada y ellos utilizaron el método de las características considerando el coeficiente de dispersión constante. Hoy en día se reconoce como algo dudoso aceptar este coeficiente constante, debido a la dinámica particular de la intrusión de agua de mar en un acuífero. Estos autores caracterizan en el problema la influencia del agua dulce y del agua salada en direcciones opuestas, en la parte más baja del acuífero, lo que resulta en un equilibrio dinámico en áreas de bajas velocidades de flujo, así como la existencia de un punto de estancamiento en el fondo del acuífero. Los resultados fueron comparados con la solución de la interfaz abrupta concluyéndose que con este modelo de dispersión la extensión de la intrusión salina es menor que con el modelo de la interfaz abrupta.
La primera solución impermanente basada en un coeficiente de dispersión dependiente de la velocidad fue desarrollada por Segol et al. (1975), la cual utiliza el método de los elementos finitos según la variante de Galerkin. Una característica distintiva de este trabajo es que la ecuación de flujo se resuelve en términos de la presión y de dos componentes de la velocidad en cada nodo de la malla, obteniendo así un campo de velocidades constante en el tiempo.
La solución impermanente de Segol también se acerca a la solución de estado permanente de Henry (1960) pero no se alcanzó debido a los altos costos de cálculo. La formulación de Segol tiene la ventaja de que garantiza la continuidad de los flujos a través de la frontera de los elementos de la malla, pero tiene la desventaja de que hay que resolver un sistema de tres ecuaciones para el flujo. Este esquema de la ecuación de flujo se conoce actualmente como el «esquema de las tres ecuaciones».
Este esquema numérico fue incapaz de predecir la intrusión por la consideración de los parámetros que describen las condiciones reales de campo, debido a las dificultades numéricas. No obstante, los resultados obtenidos por Segol confirmaron la existencia de la circulación de agua salada en los acuíferos costeros. Probablemente, la solución de Segol sea la más rigurosa de las soluciones existentes hasta ese momento y sirve como punto de referencia de gran valor ante cualquier otra solución con la que se pueda comparar.
Otro modelo alternativo fue introducido por Huyakorn and Taylor (1976). El modelo propuesto fue formulado utilizando, como variables incógnitas dependientes, a la carga hidráulica referida al agua dulce y a la concentración de sal. Ellos demostraron que esta formulación es una de las más apropiadas para ser extendida a tres dimensiones.
En todos los problemas de modelación del transporte de contaminantes cuando la advección predomina sobre la dispersión, se pueden presentar problemas de oscilaciones o de dispersiones numéricas. Una forma de poder reducir o eliminar las oscilaciones y la dispersión numérica es pasando los términos convectivos para el miembro de la derecha de la ecuación del transporte formando parte de los términos independientes y así se calcula dentro del proceso iterativo (Taylor and Huyakorn 1978).
En Cuba, la experiencia de varios autores en la modelación regional del flujo del agua subterránea en acuíferos cársicos ha llevado a afirmar que estos medios pueden ser simulados como un medio poroso equivalente. Apoyándose en la tecnología AQÜIMPE (Martínez 1988), estas hipótesis han sido aplicadas en Cuba con resultados satisfactorios según se reporta en los trabajos de Martínez (1988) y Hernández (1991).
En Cuba no existe experiencia en la modelación de la intrusión salina a partir de un modelo que tenga en cuenta la dispersión hidrodinámica. Marón (2001) ha desarrollado el modelo numérico AQUISAL que modela matemáticamente la intrusión salina con dispersión hidrodinámica siguiendo en su construcción ideas similares al modelo de Huyakorn and Taylor (1976). Por lo cual, el objetivo de este trabajo es comenzar a estudiar e introducir las ideas fundamentales de este modelo numérico en el ámbito de los especialistas e investigadores de este tema, a partir del trabajo desarrollado por Marón (2001).
Primeramente, en este trabajo se muestran las ecuaciones que intervienen en el modelo matemático, las hipótesis sobre las cuales se formula el modelo y las ideas generales del algoritmo de cálculo.
Posteriormente, para la comprobación de los algoritmos se muestra la aplicación del modelo en dos ejemplos reportados en la literatura, Huyakorn et al. (1987), el primero en un acuífero confinado y el segundo en un acuífero libre.
MODELO MATEMÁTICO AQUISAL
El conjunto de ecuaciones que conforman el modelo matemático AQUISAL se puede resumir en las siguientes ecuaciones de la (2) a la (6).
![]()
![]()
![]()
![]()
![]()
Donde: θ es la porosidad del medio (adimensional), ρ es la densidad del fluido (kg/m3), v es el vector de la velocidad real del fluido (m/día), SS es el coeficiente de almacenaje específico (1/m), h(x, z, t) es la función carga hidráulica (m), C(x, z, t) es la función concentración de sal (kg/m3), (x, z) son las variables espaciales del plano vertical (m), t es la variable temporal (día), E = 0,7 es una constante, ρ* es la densidad de la entrada y/o salida al acuífero (kg/m3), W es la entrada y/o salida (1/día), p es la presión del fluido (Pa), g es la aceleración de la gravedad (m/seg2), [KD] es la conductividad hidráulica Darciana (m/día), e es la constante e = E/ρd ( m3/kg) y [ D ] es el coeficiente de dispersión (m2/día).
A las ecuaciones anteriores hay que añadirle la geometría de la región, las propiedades hidrogeológicas del medio, las condiciones iniciales, el régimen de lluvia, el régimen de explotación al que está sometido el acuífero y las condiciones de frontera o de contorno de la región. Estas condiciones de frontera pueden ser de dos tipos: las llamadas condiciones de primera especie y condiciones de segunda especie. Las condiciones de primera especie se tienen cuando se conocen los valores de las funciones incógnitas, es decir, de las cargas o de las concentraciones en un punto o en un conjunto de puntos de la frontera. Las condiciones de segunda especie se tienen cuando se conocen los flujos del fluido o los flujos del soluto en algún tramo de la frontera. Para la ecuación de flujo las condiciones de segunda especie se pueden representar según la ecuación (7).
![]()
Donde: qL representa la velocidad del flujo de entrada o de la salida lateral por la frontera (m/día), n representa el vector normal unitario exterior a dicha frontera (adimensional), ∂h/∂t representa los cambios en el tiempo de los niveles de la superficie libre (m/día).
El término de la derivada de la carga con respecto al tiempo sólo aparece cuando el acuífero es libre y surge por la frontera superior que corresponde con la superficie libre. Para la ecuación de transporte las condiciones de segunda especie se pueden representar como ecuación (8).
![]()
Donde: qCL representa el flujo de soluto de la entrada o de la salida por la frontera.
Como puede observarse la condición de frontera (8) necesita del conocimiento de la condición de frontera del modelo de flujo dada por la ecuación (7).
En la confección del modelo AQUISAL se tienen en cuenta las siguientes hipótesis:
· medio poroso, anisótropo y heterogéneo.
· flujo lineal, impermanente y saturado.
· fluido isotérmico, incompresible y no homogéneo.
· la densidad del fluido depende linealmente de la concentración de sal según se muestra en la ecuación de estado (5).
· la viscosidad dinámica del fluido se considera constante.
· se considera la dispersión hidrodinámica, la cual puede ser considerada constante o variable en función de la velocidad del fluido.
· la ecuación de Darcy, ecuación (4), tiene la presencia de un término adicional en la componente vertical de dicha velocidad, el cual depende de la concentración del soluto.
El modelo AQUISAL es un modelo numérico que se utiliza para simular el fenómeno de la intrusión salina en un acuífero confinado o libre. Este modelo numérico está conformado por una ecuación de flujo, ecuación (2), y una ecuación de transporte de sal, ecuación (3). Ambas ecuaciones se trabajan en el plano bidimensional vertical XZ. Las variables dependientes o incógnitas son la carga hidráulica referida al agua dulce, ecuación (6), y la concentración de sal.
Ideas del algoritmo de cálculo
Como puede observarse las ecuaciones (2) y (3) son no lineales con respecto a las funciones incógnitas. En la ecuación (2) aparece la concentración de sal y en la ecuación (3) aparece la carga hidráulica, estas variables están presentes en las dos ecuaciones, por tanto es necesario un proceso iterativo para resolver las mismas. Según plantea Marón (2001), el primer paso en la confección de este modelo numérico es la aplicación del método de los elementos finitos (MEF) para la discretización en el espacio (se hace uso del triángulo lineal para la interpolación sobre cada triángulo de la malla). Esto conduce a un sistema de ecuaciones diferenciales ordinarias, que son resueltas utilizando el Método de las Diferencias Finitas (MDF) para la discretización en el tiempo con un esquema implícito (se introduce un parámetro de peso para cada una de las ecuaciones discretizadas). Las ideas fundamentales del algoritmo de cálculo se pueden resumir en los siguientes pasos:
a) Para cada paso de tiempo, se parte de una aproximación inicial de las funciones incógnitas carga hidráulica y concentración de sal {H k}r-1 y {C k}r-1. Al comienzo de cada intervalo de tiempo se toma como aproximación inicial la solución del tiempo anterior tanto para la carga hidráulica como para la concentración.
b) Se calculan las densidades con la ecuación (5).
c) Se evalúa la matriz y el término independiente del sistema de ecuaciones no lineales que se obtuvo de la ecuación (2) en las aproximaciones iniciales, convirtiéndose este en un sistema lineal de ecuaciones el cual se resuelve con respecto a la carga hidráulica, obteniéndose nuevas aproximaciones para las cargas {H k}r.
d) Con las nuevas aproximaciones calculadas de las cargas y las aproximaciones viejas de las concentraciones se calculan las velocidades del fluido con la ecuación (4).
e) Se evalúa la matriz y el término independiente del sistema de ecuaciones no lineal que se obtuvo de la ecuación (3) con las nuevas aproximaciones de las cargas y con las viejas aproximaciones de las concentraciones, convirtiéndose este en un sistema lineal de ecuaciones el cual se resuelve con respecto a la concentración de sal, obteniéndose nuevas aproximaciones para las concentraciones {C k}r.
f) Con las nuevas y las viejas aproximaciones de las cargas y de las concentraciones se calcula el máximo error absoluto, en las cargas y en las concentraciones, el cual se toma como criterio de parada con respecto a las dos funciones incógnitas,
![]()
![]()
Los valores de EH y de EC corresponden con los errores de tolerancia admitidos en las cargas y en las concentraciones en el cálculo de las iteraciones, k es la variable que representa el tiempo y la variable r representa las iteraciones.
Todos los algoritmos de cálculo fueron implementados computacionalmente en el asistente matemático MATLAB. Para más información asociada con la confección de este modelo numérico puede revisarse el trabajo de Marón (2001).
EJEMPLO ILUSTRATIVO 1
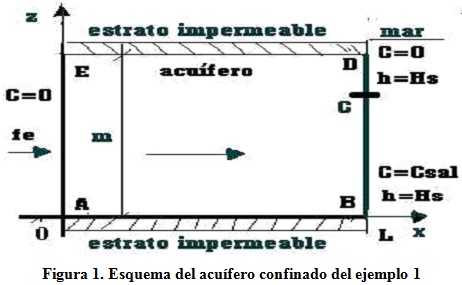
En este ejemplo se compara la solución obtenida con el modelo AQUISAL con la solución de un modelo reportado en la literatura, Huyakorn et al. (1987), para un ejemplo de intrusión salina en un acuífero confinado, isótropo y homogéneo según se muestra en la figura 1. Se consideran dos variantes del coeficiente de dispersión y se desprecia la difusión molecular.
En la figura 1 cada tramo del borde de la región rectangular tiene que estar caracterizado por dos condiciones de fronteras. Los tramos AB y DE son estratos impermeables por lo que se consideran nulos el flujo de fluido y flujo de soluto a través de estos dos lados.
Por el lado BC, que corresponde con el contacto con el agua salada, se parte de una condición de distribución hidrostática de presiones la cual depende de la profundidad z según la ecuación (11).
![]()
Donde: m es el espesor saturado del acuífero y z es la coordenada vertical, dirigida hacia arriba, que representa la elevación sobre el nivel de referencia (lado AB). Por el lado BC el agua salada penetra al acuífero, por lo tanto, la condición de frontera para el soluto en este tramo es de concentración conocida coincidiendo su valor con la concentración máxima de sal en el agua salada.
El tramo CD es la superficie de escape por la cual se supone que sale el agua dulce del acuífero y que por lo tanto no debe haber entrada de agua salada. Según plantea Huyakorn, en la práctica es muy difícil garantizar esta última condición además de que no se conoce exactamente la longitud o el espesor de este lado CD. Huyakorn simula este tramo poniendo la misma condición de carga conocida de Hs utilizada en el lado BC, pero para el soluto plantea una condición de flujo de soluto nulo. Según la ecuación (8) el flujo de soluto, qCL, es la suma de la componente convectiva del flujo y la componente dispersiva del flujo. En el modelo AQUISAL para poder trabajar con una condición de frontera de flujo de soluto es necesario conocer también el flujo del fluido por dicho tramo, es decir, si se conoce qCL por un tramo de frontera entonces hay que conocer también qL por ese tramo según se observa en la ecuación (8). El problema aquí radica en que el flujo del fluido qL no es conocido a priori por este tramo, por lo que aquí los autores decidieron tomar la decisión de sustituir la condición de Huyakorn por la condición de concentración conocida nula en dicho tramo.
En el tramo AE se considera una velocidad o flujo constante fe entrando al acuífero según la condición (7) y la concentración se considera nula, ya que este lado corresponde con la frontera del agua dulce.
Los valores de otros datos considerados en este ejemplo son los siguientes: longitud del acuífero 200 m, espesor saturado del acuífero 100 m, porosidad θ = 0,35 y concentración máxima de sal en el agua salada Cmax = 35 kg/m3; componentes de la conductividad hidráulica Darciana KD = 1 m/día (se ha adoptado un medio homogéneo e isótropo), el flujo de entrada al acuífero por el lado AE tiene el valor de fe = 0,0066 m/día. El estado inicial de las cargas se tomó igual al espesor saturado del acuífero 100 m y el estado inicial de las concentraciones se tomó nulo para todos los nodos de la malla.
Huyakorn tomó una malla uniforme con Nx = 10 subintervalos en el eje horizontal y Nz = 10 subintervalos en el eje vertical para la discretización en el espacio. Según su modelo la longitud de la superficie de escape, lado CD, es desconocida a priori y solo puede ser calculada experimentalmente con ayuda de muchas corridas del programa. Por ello, fijó una longitud de la superficie de escape de 20 m, la cual se tomó igual en el modelo AQUISAL.
El coeficiente de dispersión [D] es la suma de una componente convectiva y de una componente difusiva. La componente convectiva es función de las componentes del vector velocidad del fluido, de la dispersividad longitudinal y de la dispersividad transversal. La componente difusiva es función de la difusión molecular y de la tortuosidad del medio. Huyakorn teniendo en cuenta estas dos componentes tomó para la simulación dos variantes del coeficiente de dispersión:
· Variante 1: se considera el coeficiente de dispersión variable porque se toma la dispersividad longitudinal αL = 3,5 m, la dispersividad transversal αT = 3,5 m y la difusión molecular es nula.
· Variante 2: se considera el coeficiente de dispersión constante ya que se suponen nulas la dispersividad longitudinal αL y la dispersividad transversal αT y se toma la difusión molecular Dm = 0,066 m2/día.
En la variante 1, para la discretización en el tiempo, Huyakorn tomó un primer incremento en el tiempo de Ät = 10 días y a partir de este valor los otros intervalos los calculó multiplicando por un factor de 1,2 durante los primeros 25 intervalos y a partir de ahí tomó 10 intervalos más, iguales al último intervalo calculado, lo cual hace un número total de tiempos Nt = 35 y un tiempo final de simulación de 12669,4956 días (aproximadamente igual a unos 35 años). Este análisis generalmente se hace para garantizar la estabilidad numérica para el comienzo de los primeros tiempos de corridas.
En la variante 2, para la discretización en el tiempo, Huyakorn tomó un primer incremento en el tiempo de Δt =10 días y a partir de este valor los otros intervalos los calculó multiplicando por un factor de 1,2 durante los primeros 25 intervalos pero a partir de ahí ahora tomó 25 intervalos más iguales al último intervalo calculado lo cual hace un número total de tiempos Nt = 50 y un tiempo final de simulación de 24594,0226 días (aproximadamente igual a unos 68 años).
Resultados de la variante 1
En la figura 2 se muestran las curvas de nivel de las cargas para el tiempo final de simulación según el modelo propuesto (izquierda) y según el modelo de Huyakorn (derecha). Las curvas de nivel de las cargas del modelo AQUISAL tienen una buena semejanza con las curvas de nivel de las cargas del modelo de Huyakorn. Las diferencias en 100 metros de los valores de las curvas de nivel de ambos gráficos radican en que Huyakorn toma su nivel de referencia en el lado superior mientras que en el modelo AQUISAL el sistema de referencia es el fondo.
En la figura 3 se puede observar que la curva de concentración C = 17,5 kg/m3 del modelo AQUISAL se aproxima a la curva adimensional C/Cmax con valor 0,5 del modelo de Huyakorn. El pie de la cuña de intrusión salina para el modelo propuesto se encuentra a 100 metros del mar que es la misma distancia a la que está el pie de la cuña para el modelo de Huyakorn. Es bueno señalar que para lograr esta aproximación se adoptó el valor de la dispersividad longitudinal αT = 1,75 m, debido a que las dispersividades longitudinal y transversal son parámetros que influyen en el modelo pero se desconocen sus valores a priori. Por tanto, para lograr este mejor ajuste y que el punto de intersección entre la curva y el fondo del acuífero se encuentre a la distancia de 100 m, se decidió variar dicho valor hasta lograr alcanzar los resultados mostrados.
Resultados de la variante 2
En la figura 4 se muestra la curva de concentración 17,5 kg/m3 según el modelo propuesto y la curva adimensional C/Cmax con valor 0,5 según el modelo de Huyakorn, ambas para el tiempo final de simulación. Estas dos curvas se encuentran por debajo de la curva de la interfaz abrupta.
El modelo AQUISAL tiene la posibilidad de representar el campo de vectores de los flujos o velocidades tanto para el fluido como para el soluto. El campo de velocidad del flujo del fluido se calcula con la ecuación de Darcy, ecuación (4), mientras que el campo de velocidad del flujo del soluto se calcula con la ecuación (8). Por lo tanto, en la figura 5 se muestran los campos de flujo del fluido y del soluto solamente según el modelo propuesto ya que Huyakorn no muestra este tipo de gráfica en su trabajo. La gráfica de la izquierda, muestra un flujo que sale del acuífero por la esquina derecha superior y en la gráfica de la derecha se muestra un flujo que entra al acuífero por la esquina derecha inferior. En la gráfica de la derecha se percibe el predomino del flujo del soluto ya que en esa zona es mucho menor el flujo del agua dulce, mientras que en la gráfica de la izquierda ocurre lo contrario, existe un predominio del flujo del agua dulce.
EJEMPLO ILUSTRATIVO 2
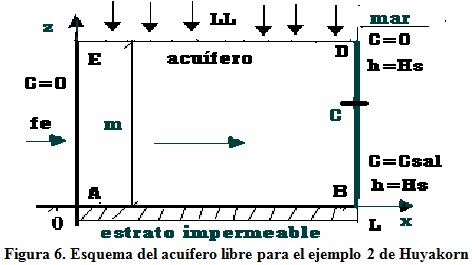
Este ejemplo corresponde con un segundo ejemplo reportado en la literatura por Huyakorn et al. (1987). La figura 6 muestra la región de flujo correspondiente con un acuífero libre que recibe un aporte por la superficie libre de una lluvia constante.
Se considera el siguiente juego de datos: longitud 200 m, espesor saturado inicial 50 m, porosidad 0,25, conductividad hidráulica, en la dirección de x, KDx = 4 m/día, conductividad hidráulica en la dirección de z, KDz = 0,4 m/día, flujo de entrada por el lado AE con valor fe = 0,004 m/día, la intensidad de la lluvia es 0,002 m/día, dispersividad longitudinal αL = 10 m, dispersividad transversal áT = 5 m y la difusión molecular es nula.
Se plantea que la longitud de la superficie de escape (lado CD) es de 30 m por lo que en la discretización esta superficie queda determinada por 6 elementos de 5 m de lado cada uno y la zona por debajo de la misma (lado BC) es de 20 m y queda determinada por 4 elementos de 5 m cada uno. La discretización en el tiempo y en el espacio se tomó similar a la variante 1 del ejemplo del trabajo anterior (Marón 2001), así como los errores de los cálculos. En la figura 7 se muestran las gráficas de los resultados de ambos modelos para el tiempo final de simulación.
Se puede observar en la figura 7 que el pie de la curva 0,5 se encuentra a unos 112 m aproximadamente de la frontera del agua dulce y la del modelo propuesto está a una distancia aproximadamente igual de dicha frontera. La profundidad del punto que intercepta la interfaz abrupta con la frontera de agua dulce es de 42 m considerando una carga en dicho punto de 1,05 m mientras que en el modelo propuesto está en el mismo rango como puede verse en la figura 7.
El punto que intercepta la curva 0,5 con la frontera de agua salada se encuentra entre los 30 y 35 m aproximadamente y para el modelo propuesto está en dicho rango también. Es bueno señalar que la superficie de escape inicial, lado CD de 30 m de longitud, tuvo que ser reducida a 20 m de longitud debido a que no se alcanzó el ajuste mostrado.
CONCLUSIONES
· Se presenta un modelo numérico, desarrollado en Cuba, que es el resultado de resolver la ecuación de flujo y la ecuación del transporte de sal aplicando el Método de los Elementos Finitos en el espacio y el Método de las Diferencias Finitas en el tiempo. El modelo es 2D en el plano vertical y permite simular el fenómeno de la intrusión salina con dispersión hidrodinámica. La dispersión hidrodinámica supone que el agua dulce y el agua salada se mezclan formándose una zona de dispersión en la cual varia la densidad del fluido. Esto hace que la modelación de la intrusión salina por esta vía se acerque mucho más a la realidad de lo que ocurre en este fenómeno con respecto a la suposición de una interfaz abrupta debida al cambio de la densidad.
· Se comprobaron los algoritmos de cálculo con la comparación entre el modelo numérico propuesto AQUISAL y dos ejemplos reportados en la literatura, comprobándose que los resultados alcanzados con el modelo AQUISAL son satisfactorios y reproducen con muy buena aproximación las curvas de nivel de las cargas y de las concentraciones de sal de los ejemplos utilizados. Es bueno señalar que los dos ejemplos reportados en la literatura presentaban todos los datos necesarios para el modelo numérico muy bien definidos, lo cual no siempre se cumple.
· Se mostró que la curva de nivel de la concentración de sal, C = 17.5 kg/m3, obtenida por el modelo propuesto no coincide con la obtenida por el modelo de la interfaz abrupta según la figura 4 (izq.) y figura 7 (izq.).
· Se obtuvo también el campo de flujo, del fluido y del soluto, obtenidos según el modelo propuesto. El campo de flujo del fluido mostró la presencia de una zona de escape hacia el mar del agua dulce, figura 5 (izq.), mientras que el campo de flujo del soluto mostró un flujo ascendente del agua salada que penetra al acuífero por la frontera de la derecha, figura 5 (der.). Todos estos resultados obtenidos pueden resultar útiles para concebir medidas de protección del acuífero.
REFERENCIAS BIBLIOGRÁFICAS
1. Henry H. R. «Salt Water Intrusion into Coastal Aquifers», Int. Assoc. Sci. Hydrol., vol.52, pp. 478-487. (1960).
2. Hernández A. O. «La explotación de acuíferos a escala regional y la modelación matemática como su base tecnológica», Tesis doctoral, Facultad de Ingeniería Civil, Instituto Superior Politécnico José Antonio Echeverría (Cujae). Habana. (1991).
3. Hubbert M. K., «The theory of ground-water motion», Journal Geol. (1940), 48 (8): 785-944, University of Chicago Press, USA.
4. Huyakorn P. S. and Taylor C. «Finite element models for coupled groundwater flow and convective dispersion», Proc.1st, Int. Conf. on Finite Elements in Water Resources, Princeton University, Princeton, N. Jersey, USA. (1976).
5. Huyakorn P. S., Andersen P. F., Mercer J. W. and White H. O. «Saltwater intrusion aquifers: Development and testing of a three dimensional finite element model», Water Resources Research, (1987), vol. 23, no. 2, pp. 293-312, American Geophysical Union, USA.
6. Marón D. E. «Aplicación del método de los elementos finitos (MEF) y del método de las diferencias finitas (MDF) en modelos de flujo y de transporte de contaminantes con densidad constante o variable en medios porosos saturados», Tesis doctoral, Facultad Ingeniería Civil, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana. (2001).
7. Martínez J. B. «Reflexiones sobre la modelación de acuíferos en las condiciones de Cuba», Memorias del XIII Congreso Latinoamericano de Hidráulica, IAHR, pág. 264-271, Habana. (1988).
8. Pinder G.F. and Gray W.G. «Finite element simulation in surface and subsurface hydrology», Academic Press Inc., ISBN 0-12-556950-5, San Diego, California, USA. (1977)
9. Segol G., Pinder G.F. and Gray W. G. «A Galerkin finite element technique for calculating the transient position of the saltwater front», Water Resources Research, (1975), vol. 11, no. 2, pp. 343-347, American Geophysical Union, USA.
10. Taylor C. and Huyakorn P. S. «Three dimensional groundwater flow with convective dispersion», in Finite Elements in Fluids, (1978), vol. 3, chapter 17, pp. 311-321, edited by R. H. Gallagher, John Wiley, New York.
Recibido: 8 de septiembre de 2015.
Aprobado: 26 de julio de 2016.
Dr. David Ernesto Marón Domínguez, Ing. Odet Caridad Herrera Betancourt, Ing. Ysnayan Fernández Legón, Ing. Lemuel Carlos Ramos Arzola, Dr. Armando Orestes Hernández Valdés. Centro de Estudios Matemáticos, Univ. Tecn. de La Habana José Antonio Echeverría (Cujae). Grupo Empresarial Investig., Proy. e Ing, Inst. Nac. Recursos Hidráulicos (INRH), Habana. Empresa Aguas de la Habana, Habana, Cuba. Centro de Investig. Hidráulicas, Univ. Tecn. de La Habana José Antonio Echeverría (Cujae). email: dmaron@cemat.cujae.edu.cu, email: odet@geipi.hidro.cu , e-mail: expysnayan@ahabana.co.cu, email: lemuel@cih.cujae.edu.cu, email: ahernandez@cih.cujae.edu.cu