Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Hidráulica y Ambiental
versión impresa ISSN 1680-0338
riha vol.38 no.1 La Habana ene.-abr. 2017
ARTÍCULO ORIGINAL
Modelación matemática de procesos morfológicos en playas con rompeolas sumergidos
Mathematical simulation of morphological processes in beaches with submerged breakwaters
Luis F. Córdova López,I Kenia Hernández Valdés,II Héctor Benítez Cristiá,I
I Centro de Investigaciones Hidráulicas. Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae)
II Inversiones Gamma S.A. La Habana, Cuba.
RESUMEN
El incremento y desarrollo de las inversiones asociadas al turismo de sol y playa, unido al aumento de la población en la zona costera a nivel mundial, hacen que cada día cobre mayor importancia conocer el comportamiento de la interacción entre el oleaje y las estructuras de defensa costera, unido a la necesidad de pronosticar de forma rápida y correcta los procesos morfodinámicos que ocurren ante situaciones extremas. El presente trabajo evalúa la capacidad del modelo matemático XBeach de simular la interacción oleaje-rompeolas sumergidos, simulando el comportamiento de un conjunto de variables tanto hidrodinámicas como morfológicas, lo que pone a prueba la capacidad del modelo para reproducir los fenómenos que ocurren en las playas ante la presencia de rompeolas sumergidos.
Palabras clave: modelación matemática, procesos morfológicos, rompeolas sumergido.
ABSTRACT
The increment and development of investments associated with sun and beach tourism, together with population increase in coastal areas at world level, make that every day bigger importance is given to know the behavior of the interaction between the surf and the structures of coastal defense, together with the need of predicting in a quick and correct way the morphodinamics processes happening under extreme situations. The present work evaluates the capacity of the mathematical model XBeach for simulating the interaction wave - submerged breakwater by simulating the behavior of a group of hydrodynamic as well as morphological variables, which tests the capacity of the model to reproduce phenomena happening on the beaches under the presence of submerged breakwaters.
Key words: mathematical model, morphological processes, submerged breakwater.
INTRODUCCIÓN
Cuba es afectada anualmente por numerosos eventos climatológicos, entre los que se destacan los frentes fríos, las bajas extra tropicales y las tormentas tropicales, que provocan severos daños en las zonas costeras (Córdova 2014). En las últimas décadas, los rompeolas sumergidos han incrementado su popularidad como obras de defensa costera debido al bajo impacto que desde el punto de vista estético y paisajístico introducen en las playas, comparado con los rompeolas emergidos. Por otra parte, actúan como un filtro para el oleaje donde las olas de menor altura consiguen atravesarlo sin una disminución significativa de su energía mientras que las de mayor altura rompen perdiendo gran parte de ésta, lo que permite un mejor intercambio de agua en la zona que se encuentra a su abrigo, además de que su construcción resulta más económica por requerir menos volumen de materiales.
A pesar de estas ventajas, existe la necesidad de comprender el comportamiento hidráulico de los complejos mecanismos de interacción que ocurren entre estas obras y el oleaje, con el objetivo de predecir los fenómenos morfológicos que se generan en la playa causados por los diferentes procesos que tienen lugar. Ranasinghe and Turner (2006) destacan que a pesar de la construcción de estas obras como alternativa para la protección costera en diversas regiones, la mayoría de los casos reportaron procesos erosivos, demostrando que los mecanismos hidrodinámicos y de transporte de sedimentos asociados con los rompeolas sumergidos son completamente diferentes de los que se generan ante los rompeolas emergidos.
En este sentido, el grupo de Ingeniería Costera y Marítima del Centro de Investigaciones Hidráulicas, desarrolló una investigación con el objetivo principal de evaluar las prestaciones del modelo Xbeach (Roelvink et al. 2009) para simular la interacción oleaje-estructuras de protección costeras, debido a su capacidad de simular la hidrodinámica y la morfología, lo que constituye una herramienta de diseño para proponer actuaciones en el manejo integrado de la zona litoral (Hernández y Córdova 2015). El presente trabajo forma parte de la investigación, donde se evalúa el comportamiento de los rompeolas tanto emergidos como sumergidos en la protección de playas, y en él se reflejan los principales resultados obtenidos de la modelación de los rompeolas sumergidos. El caso de los rompeolas emergidos y las principales diferencias en el funcionamiento de estas obras serán abordados en posteriores publicaciones.
DISEÑO DE LA INVESTIGACIÓN
Establecimiento de la malla de trabajo y variables a estudiar
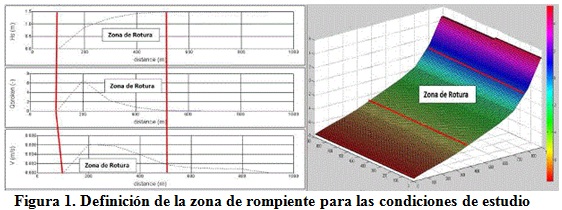
Para conocer la capacidad de reproducir los fenómenos asociados con la interacción oleaje-estructura desde el punto de vista hidrodinámico y morfológico, se realizaron una serie de simulaciones utilizando una malla regular de 900 x 900 m de longitud, con resolución de 5 m en la dirección perpendicular a la costa (dx) y de 10 m a lo largo de la costa (dy), la cual presenta batimetrías rectas y paralelas con pendientes suaves y cotas que transitan desde la profundidad de -7,6 m hasta los 5,3 m por encima del nivel medio del mar. En la investigación se estableció una altura de ola de 1,5 m, período 9 seg, dirección del oleaje incidente de 2700 sin variación del nivel medio del mar y material de fondo arena, con un tamaño de grano D50 de 0,25mm. La malla permitió visualizar los procesos ocurridos en cada simulación, contando con un área de estudio de 810 000 m2, lo que puede apreciarse en la figura 1.
Los rompeolas sumergidos presentaron un dimensionamiento de 10 m de ancho y 100 m de longitud, de sección trapezoidal con talud 1:1,5 ubicados a diferentes distancias de la costa, cumpliendo con la condición previamente estudiada que los mismos se encontraran dentro de la zona de rotura como se observa en la figura 1 en su parte izquierda, donde se presentan mediante tres gráficos el comportamiento de la altura de ola (Hs), porciento de olas que rompen (Qbroken) y el comportamiento de los velocidades de las corrientes asociadas con el fenómeno de rotura de la ola (V). En la tabla 1 y en la figura 2 se refleja la ubicación de los rompeolas sumergidos estudiados, características y cota de coronación.
Con el objetivo de evaluar las simulaciones realizadas por el modelo matemático Xbeach en los diferentes casos de estudio, se seleccionaron para su análisis un conjunto de variables tanto hidrodinámicas como morfológicas, las que se muestran en la tabla 2. Para realizar la comparación de las variables seleccionadas con la presencia de la estructura, y en ausencia de la misma, se seleccionaron dos perfiles los cuales se señalan en la figura 2.
COMPORTAMIENTO DE LAS VARIABLES ANALIZADAS
Altura de ola
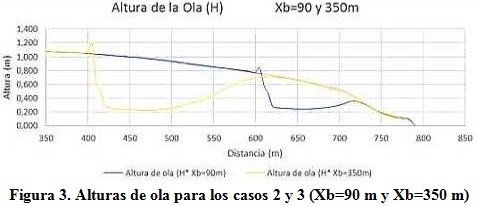
En cuanto a esta variable, para el caso 1 con una distancia a la costa Xb=50 m, la altura de ola prácticamente no es afectada por el rompeolas, lo que evidencia la poca protección que ofrece. Los casos 2 y 3, con distancias a la costa de 90 m y 350 m se comportan de manera similar, provocando el decrecimiento de la altura de ola a casi 0,2 m independientemente de que están a diferentes profundidades. Antes de llegar a la costa se incrementan los valores, alcanzando cotas de 0,3 y 0,7 m respectivamente, lo que muestra que la refracción es menor en la medida que la estructura se encuentra más cercana a la costa, figura 3.
Velocidades de las corrientes
En el caso 1 con una distancia a la costa Xb=50 m, la figura 4 muestra el comportamiento de los vectores de velocidad de las corrientes una vez realizada la modelación, donde se observa cómo aumentan sobre el área que ocupa el rompeolas, generándose grandes velocidades debido a la reducción del tirante, a la pérdida de energía del oleaje en el proceso de rotura y al proceso de difracción, llegando a alcanzar valores de hasta 2 m/s. Estas corrientes retornan mar afuera por las zonas lindantes con valores aproximados a 0,1 m/s, arrastrando el sedimento de la zona protegida lo que provoca procesos erosivos y a su vez el retroceso de la línea de costa, tal como lo describen Ranasinghe and Turner (2006), Vlijm (2011) y Hernández (2014).
El caso 2 con una distancia a la costa Xb=90 m, muestra cómo los vectores de velocidad de las corrientes alcanzan valores de 1,5 m/s, menores que los reportados en el primer caso. Se presentan patrones de circulación en cuatro celdas, coincidiendo con lo descrito por Ranashinghe et al. (2010) y Woodroof (2012) en la figura 5.
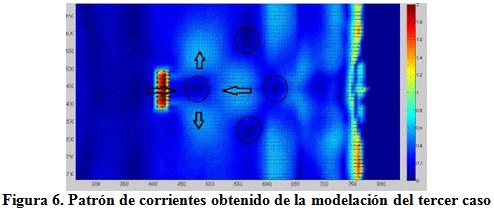
En el tercer caso, con una distancia a la costa Xb=350 m, se observan turbulencias en toda la zona protegida, y en la línea de costa las velocidades son menores en el área protegida que en las áreas adyacentes no protegidas por la estructura. La velocidad de la corriente que rebasa la estructura, con valores aproximados a 2 m/s se anula con la corriente de retorno provocando el surgimiento de nuevas corrientes hacia áreas colindantes, figura 6.
Tensiones de radiación
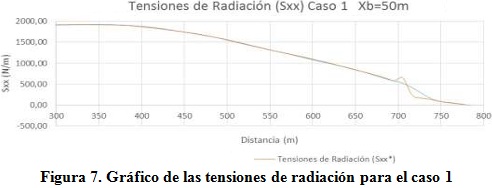
En el primer caso donde la distancia a la costa Xb=50 m (figura 7), las tensiones de radiación son poco afectadas por la estructura, donde tiene ocurrencia un máximo provocado por la rotura del oleaje sobre el rompeolas que disminuye gradualmente en dirección hacia la costa, favoreciendo el transporte transversal detrás del rompeolas.
Mientras, en el segundo caso para una distancia a la costa de Xb=90 m (figura 8), las tensiones de radiación tienen un decremento considerable detrás de la estructura con valores sobre los 1000 N/m, lo cual trae consigo que se ocasione poco transporte perpendicular a la línea de costa. Existe un pequeño incremento de las tensiones en los 50 m próximos a la línea de costa debido a que los valores de la altura de ola en esta área tienden a aumentar, lo que provoca a su vez un aumento del transporte transversal de sedimentos que pudiera ocasionar erosión y retroceso de la línea de costa. Debido a la rotura de las olas sobre la estructura se produce un máximo que facilitará la erosión justo detrás del rompeolas en la zona protegida.
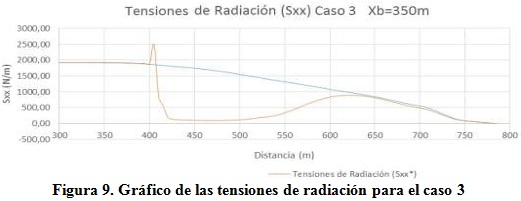
Para el caso 3, que se distingue por una distancia a la costa Xb=350 m (figura 9), el comportamiento de las tensiones de radiación es similar al caso antes descrito pero con mayores proporciones, observándose un descenso hasta alrededor de 1750 N/m llegando a valores muy pequeños detrás de la estructura, los que se mantienen a lo largo de 80 m en dirección a la costa e incrementándose posteriormente hasta alcanzar los 890 N/m. Delante de la estructura y debido a la rotura del oleaje, se observa un aumento de las tensiones que llegan a alcanzar valores de hasta 2500 N/m, lo que incrementa considerablemente el transporte de sedimentos perpendicular a la costa.
Niveles en la superficie
La presencia de rompeolas sumergidos origina una sobreelevación del nivel del mar, la cual fuerza flujos de retorno que pueden presentarse sobre la misma cresta del rompeolas, a través de las aberturas en forma de corrientes de retorno, corrientes laterales o alguna combinación de estas. Mientras la distribución de este flujo de retorno es en su mayor parte determinado por el grado de confinamiento lateral (expresado por la relación entre la longitud de la estructura Lb y la longitud de las aberturas Lg), se puede determinar su magnitud haciendo uso del balance de momento (Calabrese et al. 2008).
![]()
donde: Sxx es el tensor de radiación, P es la fuerza que la estructura ejerce en el cuerpo del
fluido y P es la presión hidrostática, según aparece en la figura 10.
Calculándose mediante las siguientes formulaciones, cuyo resultado es una simple ecuación de segundo orden en δm con una única solución positiva, la cual para el caso de fondo plano h1=h2=h se tiene:
![]()
![]()
![]()
![]()
Siendo: Kr: coeficiente de reflexión (adim.)
Kt: coeficiente de transmisión (adim.)
Hi: altura de ola incidente (m)
k: número de ola (adim.)
hb: profundidad al pie del rompeolas (m)
hc: altura de la estructura (m)
B: ancho de la corona de la estructura (m)
Ls: ancho de la base de la estructura (m)
Rc: borde libre del rompeolas (m)
Al realizar las simulaciones, en el caso 1 se presentan sobreelevaciones del nivel del mar detrás del rompeolas que alcanzan valores entre 0,03 y 0,1 m, debido fundamentalmente al desbalance de las tenciones de radiación, como muestra la figura 11.
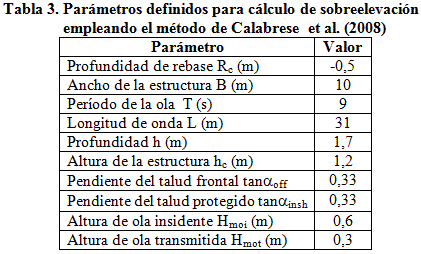
Aplicando el método propuesto por Calabrese et al. (2008) descrito anteriormente, para los datos mostrados en la tabla 3 que corresponden con los rompeolas simulados, se obtiene un valor de sobreelevación producto del desbalance de las tensiones de radiación de 0,04 m, muy similar al logrado en la simulación.
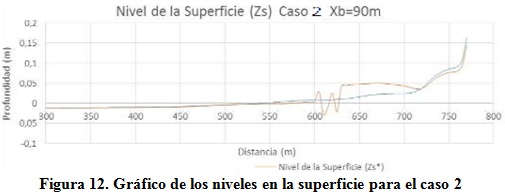
El segundo caso muestra menores valores de sobreelevación debido a que el rompeolas está más separado de la costa, llegando a valores sobre los 0,04 m, como aparece en la figura 12.
La figura 13 refleja los resultados de la simulación para el caso 3, donde los niveles alcanzan valores de 0,02 m aproximadamente, debido a que al estar más separada de la línea de costa las corrientes de retorno tienen menos influencia.
Niveles de fondo
El caso 1 se manifiesta con una fuerte erosión y el retroceso de la línea de costa, ocasionadas fundamentalmente por las corrientes que se generan sobre la estructura y que forman las celdas erosivas descritas con anterioridad, como se observa en la figura 14.
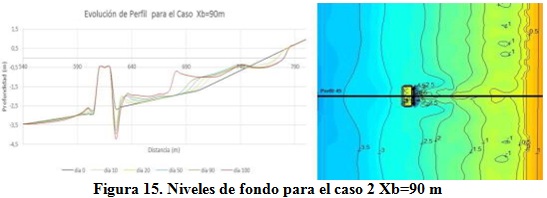
Por su parte el caso 2 se desarrolla con una notable acumulación de sedimentos en la zona al abrigo del rompeolas, con tendencias a la formación de tómbolo, lo que se evidencia en la figura 15.
Sin embargo, en el caso 3 que se muestra en la figura 16 no se observan grandes acumulaciones de sedimento y sí un retroceso de la línea de costa acompañado de socavaciones en el lado protegido por el rompeolas, lo que coincide con los patrones de socavación estudiados por Young and Testik (2009), quienes los clasifican en socavación separada y socavación adosada. Conocer el comportamiento de estos patrones y la magnitud que alcanzan reviste una gran importancia a la hora de determinar la estabilidad de los rompeolas sumergidos. En el caso que nos ocupa, se presentan patrones separados, como se refleja en la figura 17.
Transporte de sedimento
En el primer caso, la ubicación del rompeolas sumergido lejos de proteger la costa, ocasiona un proceso erosivo mucho mayor del que se produce de manera natural. Los patrones muestran que el movimiento de sedimentos se produce desde la zona protegida, donde se evidencia una fuerte erosión, hacia la parte delantera, como aparece en la figura 18.
En el segundo caso se produce una celda erosiva cercana a la estructura y una de tipo acumulativa próxima a la costa, donde se evidencia un marcado retroceso, moviéndose la arena en dirección al mar para crear la barra acumulativa, como aparece en la figura 19.
Sin embargo, en el caso 3 aunque existe erosión en la línea de costa, es menor en la zona protegida que en las áreas adyacentes. Los patrones de transporte se alejan de la costa con dirección al rompeolas, donde se anulan las corrientes que los provocan y las que rebasan la estructura, ocasionando una zona con patrones de transporte de sedimentos nulos.
Se destaca una fuerte erosión en la zona protegida cercana a la estructura, responsable de los patrones de socavación mencionados con anterioridad, lo que aparece en la figura 20.
CONCLUSIONES
· La simulación matemática de los casos de estudio definidos para la investigación utilizando el modelo Xbeach, permitió obtener diferentes respuestas morfológicas que coinciden con los resultados obtenidos por otros autores.
· En el modelo se manifiesta de manera correcta la interacción oleaje-estructura y se han logrado reproducir mediante el comportamiento de las variables tanto hidrodinámicas como morfológicas (altura de ola, niveles del mar, tensiones de radiación, niveles de fondo, transporte de sedimento y patrones sedimentación/erosión), los diferentes procesos que ocurren en los rompeolas sumergidos.
· Los niveles de la superficie obtenidos en la modelación fueron comparados con los calculados utilizando el método propuesto por Calabrese et al. (2008) para determinar la sobreelevación en rompeolas sumergidos, lo que mostró coincidencia en sus valores y el buen desempeño del modelo.
· Se destaca en la investigación la relación existente entre la distancia a la que se ubican los rompeolas y los patrones de circulación generados. Una distancia relativamente corta tiene como respuesta la formación de un patrón de dos celdas causando erosión y una distancia relativamente grande deriva en un patrón de cuatro celdas que propicia la acumulación en la costa. Estos resultados coinciden con los reportados por Ranashinghe et al. (2010).
· La aplicación de los resultados obtenidos debe limitarse al rango de valores empleados en la modelación y deben utilizarse con cautela. Son necesarias más investigaciones y una extensiva calibración/validación del modelo para arribar a conclusiones decisivas sobre la respuesta morfológica de las playas ante la presencia de rompeolas sumergidos.
· Aunque el conocimiento sobre los rompeolas sumergidos se ha incrementado en los últimos años, no existe regla alguna establecida para conocer el modo de respuesta de la costa ante la construcción de este tipo de obras, por lo que su empleo para la protección de playas debe ser cuidadosamente evaluado, no solo por la presencia de patrones erosivos sino también por los patrones de socavación observados, lo que atenta contra la estabilidad de la obra.
REFERENCIAS BIBLIOGRÁFICAS
1. Calabrese M., Vicinanza D. and Buccino M. «2D Wave setup behind submerged breakwaters». Ocean Engineering Journal, (2008), vol. 35, pp. 1015-1028. ISSN: 0029-8018, Elsevier, U.K.
2. Córdova L. «Sistema de ingeniería de costas: evaluación del proceso de erosión en la playa Varadero». Ingeniería Hidráulica y Ambiental, (2014), vol 35, no. 3, pp. 17-31, ISSN: 1815-591X, CIH, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana.
3. Hernández K. «Evaluación del modelo matemático Xbeach para la simulación de la hidrodinámica y los cambios morfológicos en las playas ante eventos extremos». Tesis presentada en opción al Máster en Ingeniería Hidráulica. CIH, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana. (2014).
4. Hernández K. y Córdova L. «Simulación matemática de la interacción oleaje-estructuras de protección costera». Ingeniería Hidráulica y Ambiental, (2015), vol 36, no. 3, pp. 74-87, ISSN: 1815-591X, CIH, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana.
5. Ranasinghe R. and Turner I. L. «Shoreline response to submerged structures: A review». Coastal Engineering Journal, (2006), vol. 53, no. 1, pp. 65-79. ISSN: 1793-6292, Elsevier, U.K.
6. Ranasinghe R., Larson M. and Savioli J. «Shoreline response to a single shore parallel submerged breakwater». Coastal Engineering Journal, (2010), vol. 57, pp. 1006-1017. ISSN: 1793-6292, Elsevier, U.K.
7. Roelvink D., Reniers Ad., Dongeren Ap., Thiel de Vries J., McCall R., Lescinski J. «Modeling storm impacts on beaches, dunes and barrier islands». Coastal Engineering Journal, (2009), vol. 56, pp.1133-1152. ISSN: 1793-6292, Elsevier, U.K.
8. Vlijm R. J. «Process-based modelling of morphological response to submerged breakwaters». A thesis submitted as partial fulfilment of the Master of Science degree in Coastal Engineering at the Delft University of Technology, The Netherlands. (2011).
9. Young D. M. and Testik F. Y. «Onshore scour characteristics around submerged vertical and semi-circular breakwaters». Coastal Engineering Journal, (2009), vol. 56, no. 8, pp. 868-875. ISSN: 1793-6292, Elsevier, U.K.
10. Woodroof K. A. «Determining the performance of breakwaters during high energy events: a case study of the Holly Beach breakwater system». Thesis of Master of Science degree in Civil and Environmental Engineering, Louisiana State University, U.S.A. (2012).
Recibido: 6 de septiembre de 2015.
Aprobado: 27 de julio de 2016.
Luis F. Córdova López, Kenia Hernández Valdés, Héctor Benítez Cristiá. Centro de Investigaciones Hidráulicas. Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Inversiones Gamma S.A. La Habana, Cuba. e-mail: cordova@tesla.cujae.edu.cu, e-mail: kenia@div.gamma.com.cu