Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Hidráulica y Ambiental
versión impresa ISSN 1680-0338
riha vol.38 no.3 La Habana set.-dic. 2017
ARTÍCULO ORIGINAL
Análisis de Fourier para mejorar un MDE destinado a simulaciones hidrológicas e hidráulicas
Fourier analysis for enhancing a DEM destined to hydrologic and hydraulic simulations
Divaldo Domingos da Silva,I Emilio Ricardo Escartín Sauleda,II Emilio Ricardo Escartín Sauleda,II
I ISPTEC-Instituto Superior Politécnico de Tecnologias e Ciências. Luanda, Angola.
II Depto. Geociencias. Fac. Ing. Civil. Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana, Cuba.
RESUMEN
El trabajo se desarrolló para un barrio de la ciudad de Luanda, a partir de la creación de un modelo digital de elevaciones (MDE) de alta resolución espacial, con datos de diversas fuentes, para la simulación de procesos hidrológicos e hidráulicos, como parte de una estrategia para el diseño de redes de drenaje pluvial, aplicando la modelación matemática. Se utilizaron herramientas del análisis de Fourier y el filtrado digital para atenuar las fluctuaciones de carácter local presentes en el MDE. En el proceso de filtrado del MDE se aseguró que el filtro escogido eliminara totalmente las fluctuaciones locales espurias, de altas frecuencias y dejara solo las componentes de tendencia deseadas, de bajas frecuencias.
Palabras clave: análisis de Fourier, filtrado digital, modelo digital de elevaciones, simulación hidrológica e hidráulica.
ABSTRACT
The work was developed for a neighborhood in the city of Luanda, on the basis of a digital elevation model (DEM) of high spatial resolution, with data from different sources, for simulating hydrologic and hydraulic processes, as part of a strategy for designing storm sewer networks applying mathematical modeling. Fourier analysis tools and filtering were used to reduce the fluctuations of local character from the DEM. In the filtering process, it was ensured that the chosen filter completely eliminated all local fluctuations of high-frequency components and leaves only the desired low-frequency trend components.
Key words: Fourier analysis, digital filtering, digital elevation model, hydrologic and hydraulic simulation.
INTRODUCCIÓN
El propósito de cualquier proceso de filtrado pasa bajas es eliminar o al menos reducir las fluctuaciones de carácter local de pequeñas dimensiones (espaciales, en el caso de un modelo digital de elevaciones, MDE). El filtrado pasa bajas de un MDE persigue el propósito de eliminar, en un modelo recién interpolado, aquellas fluctuaciones de orden local que le confieren a la superficie un carácter o apariencia «áspera» o «rugosa».
En el problema tratado en este trabajo, este paso resulta no solo conveniente, sino prácticamente imprescindible (Alfonso 1983), debido a que los métodos de interpolación de los datos producen inevitablemente este tipo de fluctuaciones. Este filtrado, al eliminar las fluctuaciones locales, retiene o destaca las componentes de tendencia suave en la superficie del modelo (Da Silva 2015).
Para escoger los coeficientes del filtro más conveniente y el modo de aplicarlo, se pueden hacer pruebas con el auxilio de algún programa informático adecuado. Los programas informáticos Surfer (Golden 2011) y especialmente MATLAB (Ingle and Proakis 1997), son ejemplos convenientes. Entre los filtros pasa bajas más utilizados para este proceso de filtrado se encuentran los llamados filtros de promediación y los filtros gaussianos, de diferentes tamaños, pero con coeficientes con simetría par en el dominio temporal (o espacial).
La experimentación con tales filtros puede incluir también la elección del procedimiento o algoritmo mediante el cual se aplica el filtro escogido sobre los datos, en este caso el MDE. Se debe tener en cuenta que cada aplicación de este tipo de filtros produce una inevitable pérdida de datos en los bordes o márgenes del modelo resultante, que depende del tamaño del filtro, por lo que aplicar un filtro de tamaño exageradamente grande, o aplicar el mismo filtro una cantidad excesiva de veces acarrea una pérdida innecesaria de datos. La extensión del modelo original más allá del área verdaderamente de interés, asegura que al final del proceso de filtrado, descontando la pérdida de datos en los márgenes, el modelo resultante se extienda exactamente al área de interés o tal vez poco más.
Con el ánimo de simplificar el contenido de este trabajo, las explicaciones y los gráficos que se presentarán a continuación corresponderán con ejemplos en 1-D; la extensión al caso 2-D se puede hacer fácilmente y sin perder generalidad, desde el punto de vista conceptual. Al final del trabajo se presentará el resultado obtenido con el MDE bidimensional objeto de interés.
CONSIDERACIONES SOBRE LOS DATOS DE PARTIDA
Se parte de un MDE interpolado a partir de datos de diferentes fuentes, que cumple con los criterios de validación de la calidad establecidos (compatibilidad del modelo con la cartografía base, validación recíproca, evaluación de residuos y criterios cualitativos), con resolución espacial escogida para la malla regular inicial de 2 m, teniendo en cuenta la densidad superficial de los puntos y al que para las simulaciones hidrológicas e hidráulicas se le hace la superposición del ambiente construido, encima del relieve natural (Da Silva et al. 2014). En la figura 1 aparece: (a) el MDE de la superficie del terreno tal como se obtuvo del proceso de interpolación, (b) el MDE mejorado con un proceso de filtrado digital y (c) el modelo digital definitivo, con las áreas construidas superpuestas y la presencia de la red vial.
CONSIDERACIONES SOBRE EL PROCESAMIENTO DE SEÑALES Y LOS FILTROS
Las observaciones cuantitativas secuenciales más comunes en Geociencias son aquellas correspondientes a escalas numéricas de relaciones o de intervalos. A toda secuencia numérica de este tipo, con un intervalo de muestreo único e invariable, y que presente un comportamiento fluctuante, se le denomina genéricamente serie temporal, independientemente de que las observaciones se realicen en el tiempo o en el espacio, como es el caso de este trabajo.
Una serie temporal puede tener múltiples dimensiones: 1-D como en el caso de un perfil del relieve, 2-D como en el caso de un MDE, 3-D como en el caso de un cubo de datos sísmicos en (x, y, t), y así sucesivamente. La representación y el procesamiento de una serie temporal puede hacerse tomando como base el comportamiento de la serie en dos dominios diferentes: el dominio del tiempo (o del espacio) y el dominio de la frecuencia (o del número de onda). Debido a la completa equivalencia entre tiempo espacio y frecuencia número de onda en el contexto del análisis de Fourier, en lo adelante se continuará con el uso exclusivo de los conceptos de tiempo o espacio y frecuencia.
La representación en el dominio de la frecuencia corresponde a la composición espectral, basada en la transformación de Fourier de la serie temporal del fenómeno bajo estudio. La comprensión de la expresión de los fenómenos en el dominio de la frecuencia no es un conocimiento común, y requiere de entrenamiento en esta materia, lo cual está más allá del objetivo de este trabajo.
Se sabe que ambos dominios: el del tiempo y el de la frecuencia resultan completamente equivalentes para el trabajo, pero la apariencia de un mismo fenómeno representado en cada uno de ellos es muy diferente, y como consecuencia, las operaciones matemáticas para procesar los datos en uno y otro dominio, presentan marcadas diferencias. La figura 2 presenta el aspecto general que tiene una serie temporal cuando se representa en el dominio del tiempo. Los ejes de estos gráficos corresponden a unidades temporales en la horizontal (resulta indiferente que sean segundos, horas, años o simplemente unidades de muestreo) y unidades de amplitud de las fluctuaciones en la vertical (resulta indiferente que sean unidades de longitud, volumen, corriente, tensión, presión u otra cualquiera). En dicha figura se muestran (a) una serie temporal periódica original, formada por la suma de funciones seno y/o coseno de frecuencias 0,02, 0,07 y 0,2 unidades normalizadas, (b) una serie (línea continua) resultante de adicionar ruido aleatorio a la serie original (línea discontinua) y (c) una serie (línea continua) resultante de adicionar una tendencia lineal de pendiente positiva muy pequeña a la serie original (línea discontinua).
En estos gráficos se pueden identificar subjetivamente tres componentes de diferentes características:
· Una componente que refleja una tendencia general (bajas frecuencias);
· Una componente de tipo estacional o cíclica (frecuencias intermedias) y
· Una componente de carácter local o aleatorio (frecuencias altas).
La representación de las mismas series temporales en el dominio de la frecuencia, queda en términos de la composición espectral o de las amplitudes de cada componente de frecuencias de la serie procesada.
La figura 3 muestra la representación de las tres series temporales en el dominio de la frecuencia. Estos gráficos son llamados espectros. En estos gráficos el eje horizontal corresponde a la frecuencia (en este caso, con valores normalizados entre 0 y 0,5), mientras el eje vertical muestra la amplitud (o su cuadrado, llamado potencia) de cada componente armónica de frecuencia. La figura 3 (a) muestra el espectro de la serie temporal original de la figura 2 (a). La figura 3 (b) muestra el espectro de la serie temporal contaminada con ruido aleatorio aditivo de la figura 2 (b).
Se aprecian las tres componentes de frecuencia de la serie original, así como la presencia de nuevas y numerosas componentes del ruido, resultantes de la adición. La figura 3 (c) muestra el espectro de la serie temporal con tendencia lineal incluida de la figura 2 (c). La tendencia lineal es interpretada como una componente de frecuencia muy baja (casi cero) y gran amplitud.
Se puede observar que la adición de esta tendencia lineal exige un cambio de la escala en el eje vertical y cómo ese cambio de escala vertical oculta o enmascara la mayoría de las componentes de menor amplitud, por lo que solo aparecen los extremos de los picos correspondientes a las componentes de frecuencias de la serie temporal original 0,02, 0,07 y 0,2.
Además, en los espectros se pueden identificar las siguientes regularidades objetivas: la tendencia, formada por componentes armónicas (senos y cosenos) de frecuencias bajas cercanas a cero, las componentes de frecuencias intermedias (llamadas cíclicas o estacionales) y las componentes de altas frecuencias, donde se concentran las fluctuaciones locales o ruidos de fondo.
El estudio riguroso de las componentes de diferentes frecuencias de una serie temporal se hace en el contexto del llamado Análisis Espectral, en el ámbito del Procesamiento de Señales e Imágenes, y sobre la base de la teoría de los Sistemas Lineales y las herramientas del análisis de Fourier (series de Fourier y transformación de Fourier).
La mayoría de los algoritmos de procesamiento de señales incluyen el diseño o la elección de filtros y la realización de procesos de filtrado. Un filtro puede ser descrito como un sistema lineal que transforma señales.
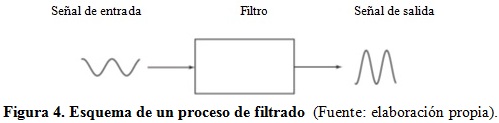
La teoría de los sistemas lineales proporciona la base matemática para el diseño y la realización de los filtros. La transformación de una señal se produce mediante la aplicación de una operación matemática, llamada «convolución», entre la señal de entrada y el operador del filtro. En la figura 4, que muestra un esquema del tipo «caja negra» de un proceso de filtrado, se puede observar cómo una señal de entrada se transforma en una señal de salida mediante la acción del filtro.
CONSIDERACIONES SOBRE EL DISEÑO DE FILTROS
El diseño de filtros digitales es un problema importante y a la vez difícil. Se remite al lector interesado a Ingle and Proakis (1997) para profundizar en estos temas. En el diseño de filtros generalmente se pueden identificar las siguientes tres etapas: especificación de las propiedades deseadas (ideales), las que son determinadas por la aplicación; la aproximación de las especificaciones usando varios conceptos y procesos matemáticos que conducen a una descripción del filtro discreto en el tiempo, y finalmente, la implementación del filtro (Ingle and Proakis 1997).
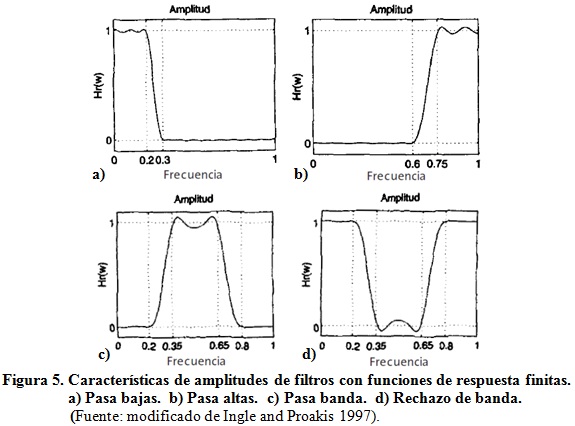
El desempeño de un filtro se puede evaluar a partir de su característica de amplitudes, que es un gráfico con simetría par en el intervalo de frecuencias considerado, generalmente normalizados entre -1 y 1 o entre -π y π, que se obtiene mediante la transformación de Fourier del operador en el dominio del tiempo. Conviene destacar que no siempre se consiguen alcanzar exactamente las características ideales deseadas. En particular, resultan de interés, por lo nocivas, las «arrugas» u ondulaciones que se presentan en la banda de rechazo de las características de amplitudes de los operadores o filtros implementados en la realidad. En la figura 5 se muestran ejemplos de las características de amplitudes para las frecuencias positivas, de cuatro filtros con funciones de respuesta finitas: (a) pasa bajas, (b) pasa altas, (c) pasa banda y (d) de rechazo. El eje horizontal representa las frecuencias normalizadas en el intervalo de cero a uno, mientras el eje vertical corresponde a la amplitud de cada componente, normalizada entre cero y uno.
Observe en cada uno de los ejemplos una banda de paso (con valores cercanos a uno), bandas de rechazo (con valores cercanos a cero) y zonas de transición entre ambas. En la etapa de implementación se obtiene la expresión del operador correspondiente, en el dominio del tiempo o de la frecuencia (por ejemplo, los coeficientes para la realización práctica del filtrado en el dominio del tiempo).
De cualquier manera, el uso de los filtros digitales es una técnica relativamente antigua y existen numerosos filtros pre-diseñados, con características bien conocidas, que pueden ser tomados de tablas y utilizados sin ninguna duda para diversas aplicaciones. Entre estos tipos de filtros sobresalen los filtros pasa bajas de promediación, por su sencillez y los gaussianos, por sus propiedades estadísticas.Figura 5. Características de amplitudes de filtros con funciones de respuesta finitas.
PROCESO DE SUAVIZACIÓN DEL MODELO DIGITAL DE ELEVACIONES Y DISCUSIÓN DE LOS RESULTADOS
Los filtros que se emplean en la suavización de imágenes, MDE o mapas son filtros pasa bajas bidimensionales. Las figura 6 y 7 muestran vistas en elevación o «ecuatoriales» parciales en 2-D de las características de amplitudes en el dominio de las frecuencias de filtros utilizados en este trabajo. El eje horizontal representa las frecuencias en la dirección X, normalizadas en el intervalo de menos uno a uno, mientras el eje vertical representa las amplitudes normalizadas en el intervalo de cero a uno. Una representación total en 2-D incluiría otro eje de frecuencias idéntico, pero en la dirección Y, perpendicular al plano de los gráficos. La figura 6 presenta las características de amplitudes de dos filtros pasa bajas bidimensionales comunes: (a) el filtro de promediación de 3x3 términos y (b) el filtro gaussiano de 3x3 términos.
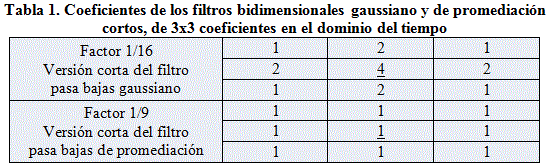
Como se puede apreciar, estos filtros cortos presentan unas características de amplitudes que denotan su baja calidad, pues la banda de paso es ancha, con zonas de transición sumamente amplias, y en las bandas de rechazo no se aproximan al valor cero deseado. Sin embargo, en la práctica es posible conseguir mejorar la característica de amplitudes de un filtro equivalente, al aplicarlo varias veces sucesivas. La tabla 1 presenta los coeficientes de los filtros bidimensionales de promediación y gaussiano de 3 x 3 términos en el dominio del tiempo.
Del análisis de los coeficientes de la tabla 1 se puede inferir que:
· El filtro Gaussiano da un mayor peso (4/16 = 1/4) al punto central de la vecindad (subrayado), en comparación con los puntos periféricos.
· El filtro Gaussiano suaviza más lentamente.
· El filtro de promediación es más «imparcial» o «democrático», por atribuirle a todos los puntos de la vecindad el mismo peso (1/N, con N=9 en este caso).
· El filtro de promediación suaviza más rápidamente.
Como ambos filtros tienen características de amplitudes de baja calidad (zonas de transición anchas, pendientes no muy pronunciadas y zonas de rechazo muy diferentes de cero), es conveniente buscar una alternativa que permita mejorar la calidad de los resultados, y aun sin despreciar un operador de baja calidad conocido, evite la necesidad de adentrarse en las complejidades del diseño de un nuevo filtro.
El procedimiento existe, se emplea exitosamente con relativa frecuencia y con varios objetivos, y consiste en aplicar el mismo filtro sucesivamente una cierta cantidad de veces, lo que equivale a utilizar filtros equivalentes con mejores características de amplitudes (Alfonso 1983, Sección 10.6).
Para verificar este mecanismo, se probaron los filtros pasa bajas gaussiano y de promediación, de tamaños 3x3 (9 términos) y se hicieron operar sobre ellos mismos diferentes cantidades de veces. La figura 7 muestra las características de amplitudes de los filtros equivalentes resultantes de la convolución con ellos mismos, lo que equivale a la aplicación sucesiva de los filtros de la figura 6, en este caso diez veces consecutivas. En la figura 7 (a) el filtro obtenido a partir del filtro de promediación, con 21x21 coeficientes y en la figura 7 (b) el filtro obtenido a partir del filtro gaussiano, con 21x21 coeficientes.
Se puede demostrar que entre los operadores originales y equivalentes se cumple la siguiente relación, ecuación (1):
![]()
donde: Horig(ω) y Heqiv(ω) son las características de amplitudes de los operadores original (figura 6) y equivalente (figura 7), respectivamente, y N es la cantidad de veces que se aplica el operador original de manera sucesiva.
Esta relación explica por qué el operador equivalente presenta mejores propiedades, con una banda de paso más estrecha y esbelta, y se reducen las ondulaciones en la banda de rechazo, en la que las amplitudes se aproximan al nivel de amplitud cero. Mientras mayor sea el valor de , más estrechas y esbeltas se harán las bandas de paso del filtro equivalente resultante, más estrechas y abruptas las pendientes de las zonas de transición y más cercanos a cero los niveles de amplitud en las bandas de rechazo. Igualmente, el filtro equivalente tendrá una mayor cantidad de coeficientes en el dominio del tiempo.
En vista de los resultados obtenidos en estas pruebas, se decidió escoger como filtro definitivo el equivalente de la figura 7 (a), por presentar una característica de amplitudes con banda de paso más estrecha y esbelta -en el intervalo (-0,4; 0,4)- y con unas bandas de rechazo más anchas -para frecuencias en los intervalos (-1; -0,4) y (0,4; 1)- obtenido a partir del filtro de promediación de 3x3 coeficientes, aplicado 10 veces sucesivas sobre el MDE, teniendo en cuenta que se va a producir una pérdida de 10 puntos por cada lado o margen del modelo de elevaciones, ya que el filtro equivalente tendrá 21 coeficientes en el dominio del tiempo.
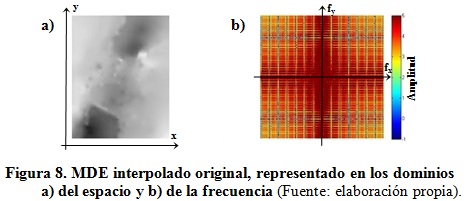
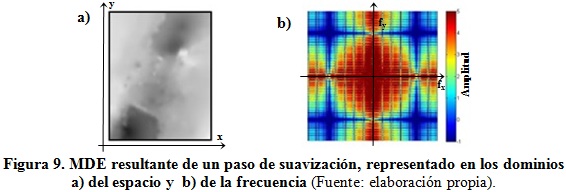
Por medio de las figuras 8, 9, 10 y 11 se pueden evaluar algunos resultados parciales y el resultado final del proceso de filtrado desarrollado, desde el MDE original interpolado, hasta el modelo suavizado con el filtro equivalente definitivo, resultante de aplicar el filtro corto de promediación diez veces consecutivas. En dichas figuras aparecen las vistas en planta de (a) los MDE en el dominio del espacio, en escala de grises con máximos en gris claro y mínimos en gris oscuro, y (b) los espectros de amplitudes de los MDE en el dominio de la frecuencia (con frecuencia cero en el centro y frecuencias altas en los bordes de las figuras, y ejes normalizados en el intervalo de Nyquist), en una escala de colores para la amplitud normalizada, que va desde el azul oscuro para la amplitud mínima (-1), hasta el valor de amplitud máxima (5) en rojo.
En la figura 8 (a) se muestra el modelo original resultante de la interpolación, el mismo de la figura 1 (a). Se observa claramente la presencia de numerosas manchas claras (elevaciones) y oscuras (hundimientos), asociadas a fluctuaciones locales de altas frecuencias. En la figura 8 (b) se observa la presencia de componentes de frecuencias bajas (hacia el centro de la figura), medias y altas (hacia los bordes de la figura). Los colores rojos predominantes corresponden a componentes con amplitudes grandes en todos los intervalos de la frecuencia.
La figura 9 muestra el MDE resultante de un paso de suavización. Obsérvese en la representación en el dominio del espacio (a) la permanencia de numerosas manchas asociadas a fluctuaciones locales de altas frecuencias y la pérdida de pocos datos en el margen del modelo. En la representación en el dominio de la frecuencia (b) se aprecia la presencia de componentes de grandes amplitudes y frecuencias bajas (colores rojos hacia el centro de la figura), pero comienzan a desaparecer componentes de frecuencias medias y altas (colores azules hacia los bordes de la figura).
En la figura 10 se muestra el MDE resultante de cinco pasos de suavización. En la representación en el dominio del espacio (a) se observa la permanencia de relativamente pocas manchas asociadas a fluctuaciones locales de altas frecuencias y la pérdida de aún más datos en el margen del modelo. En la representación en el dominio de la frecuencia (b) se observa la presencia de componentes de frecuencias bajas y medias (colores rojos hacia el centro de la figura), pero aún conserva zonas con componentes de amplitudes relativamente grandes (amarillo y naranja) en un fondo de bajas amplitudes (azules) hacia las altas frecuencias (bordes de la figura).
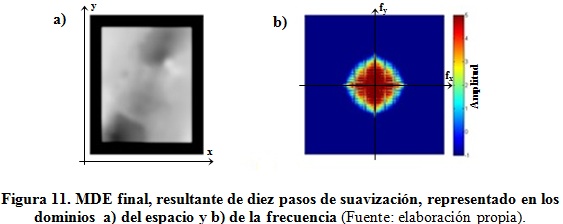
Finalmente, en la figura 11 se hace la representación del MDE tomado como definitivo, resultante de haber sido sometido a diez pasos de suavización. En la representación en el dominio del espacio (a) se observa -al igual que en la figura 1 (b)-, por un lado la disminución apreciable de las manchas asociadas a fluctuaciones locales de altas frecuencias y por el otro, la pérdida apreciable de datos en el margen del modelo, si se compara con la figura 8. La representación en el dominio de la frecuencia en la figura 11 (b) muestra la concentración de las componentes de amplitudes grandes alrededor de las frecuencias bajas (un pequeño círculo de colores rojos al centro de la figura), y la ausencia total de componentes de medias y altas frecuencias (color totalmente azul hacia los bordes de la figura).
Los resultados alcanzados muestran la utilidad de las herramientas del análisis de Fourier y el filtrado digital para reducir o eliminar el efecto de las fluctuaciones espaciales nocivas de carácter local y destacar las componentes de tendencia que resultan de mayor interés en los MDE. Estos resultados se aprecian tanto en la secuencia de las figuras 8, 9, 10 y 11, como en la figura 1.
CONCLUSIONES
· En el presente trabajo se consigue mejorar la calidad de un MDE destinado a simulaciones hidrológicas e hidráulicas haciendo uso exitoso de herramientas del análisis de Fourier y del filtrado digital. Las pruebas efectuadas muestran que cuando se dispone de un filtro corto, con características de amplitudes de baja calidad, la aplicación del mismo filtro una cierta cantidad consecutiva de veces , produce un resultado de mayor calidad que la aplicación de dicho filtro una sola vez.
Este procedimiento sencillo es equivalente a utilizar un filtro de mayor tamaño, y lo más importante, evita la necesidad de diseñar un nuevo filtro, lo cual resulta más complicado, pues exige conocimientos específicos. En particular, las pruebas efectuadas demuestran que el filtro pasa bajas bidimensional de promediación corto, con coeficientes, aplicado 10 veces consecutivas sobre los datos, produce un resultado de mayor calidad que el filtro gaussiano equivalente.
· Los resultados alcanzados, luego del proceso de filtrado pasa bajas, muestran que en la representación del MDE en el dominio del tiempo (o del espacio) se aprecia subjetivamente una reducción de las amplitudes de las fluctuaciones locales, lo que equivale a resaltar las componentes de tendencia suave.
Esta suavización se aprecia objetivamente a través de la representación de los espectros de los MDE resultantes del filtrado. Estos espectros muestran la atenuación paulatina hasta la total eliminación de las componentes de ruidos locales de altas frecuencias, mientras permanecen inalteradas las componentes de tendencia de bajas frecuencias.
· Para determinar el área de interés en el MDE, debe tenerse en cuenta que durante el proceso de filtrado comúnmente se pierde una cierta cantidad de datos en los márgenes del MDE, que depende de la longitud del filtro original y de la cantidad consecutiva de veces que se aplica el operador.
REFERENCIAS BIBLIOGRÁFICAS
1. Alfonso J. R. «Matemática Aplicada a la Geofísica», Cap. 4-Sistemas Lineales y Cap. 10-Principios de Filtrado Digital. Depto. de Geofísica. Facultad de Ingeniería Civil. Instituto Superior Politécnico José Antonio Echeverría (Cujae). Ediciones ENSPES. La Habana, p 500. (1983).
2. Da Silva D. D. «Estrategia para el diseño de redes de drenaje pluvial, empleando la modelación matemática, para su aplicación en la ciudad de Luanda». Tesis Doctoral. Fac. de Ing. Civil. Instituto Superior Politécnico José Antonio Echeverría, (Cujae), La Habana, Cuba. (2015).
3. Da Silva D. D., Escartín E. R. y Jiménez G. C. «Creación del modelo digital de elevaciones de una zona urbana para la simulación hidrológica». Ingeniería Hidráulica y Ambiental, (2014), vol. 35, no. 2, pp. 123-137. ISSN 1815-591X, Centro de Investigaciones Hidráulicas, Instituto Superior Politécnico José Antonio Echeverría, (Cujae), La Habana, Cuba.
4. Golden «Surfer help system». Golden Software Inc., 809 14th Street, Golden, Colorado 80401-1866, USA. (disponible en: www.GoldenSoftware.com). (2011).
5. Ingle V. K. and Proakis J. G. «Digital signal processing using MATLAB volume 4». 420 p., ISBN 053-493-805-1, PWS Publishing Company, Boston, USA. (1997).
6. Trauth M. H. «MATLAB recipes for earth sciences». SpringerVerlag. ISBN 978-364-212-762-5, Berlin, Germany. (2010).
Recibido: 3 de julio de 2015.
Aprobado: 30 de septiembre de 2017.
Divaldo Domingos da Silva, Emilio Ricardo Escartín Sauleda, Gerardo Crescencio Jiménez Sáez. ISPTEC-Instituto Superior Politécnico de Tecnologias e Ciências. Luanda, Angola. Depto. Geociencias. Fac. Ing. Civil. Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana, Cuba.Depto. Ing. Vial. Fac. Ing. Civil. Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae). Habana, Cuba. e-mail: divaldosilva54@hotmail.com, e-mail: escartin@civil.cujae.edu.cu, e-mail: gjimenez@civil.cujae.edu.cu.