INTRODUCCIÓN
El estudio se efectuó en un canal de olas angosto con generador hidráulico de oleaje regular e irregular controlado por computadora; para la medición y proceso de los datos de oleaje se utilizó un ológrafo con sensores de oleaje resistivos controlado por computadora, con los que se cuenta en el Laboratorio de Ingeniería Hidráulica de la Escuela Superior de Ingeniería y Arquitectura, Unidad Zacatenco del Instituto Politécnico Nacional de México. Dentro del canal se construyó un perfil playero a fin de obtener las condiciones de profundidad para desplantar las secciones de rompeolas a probar, necesario para realizar los ensayos del estudio. Se fabricaron e implementaron dos secciones de rompeolas superficiales con las cuales se realizaron series de ensayos. Dos series de pruebas se realizaron para medir el daño sobre el talud exterior de los rompeolas para diferentes condiciones de ensayo (alturas y periodos de oleaje), todo lo anterior fundamentado con lo presentado en el estado del arte.
PARAMETROS CONSIDERADOS EN EL ESTUDIO
Oleaje incidente
Con base en datos de oleaje normal y de tormenta que corresponden a olas generadas en mar abierto, se realizó una propagación del oleaje hacia las profundidades a reproducir en el modelo. De acuerdo con lo anterior, se calcularon las características del oleaje a una profundidad de 20 m. (50 cm. condición de modelo) de los ocho diferentes espectros de oleaje con que cuenta el equipo, se utilizó el espectro de Pierson-Moskowitz para generar las señales de oleaje irregular.
Niveles del mar
El estudio consideró la condición de oleaje normal y de tormenta, el plano de referencia fue el Nivel de Bajamar Media Inferior (N.B.M.I.).
Batimetría frente al rompeolas
Debido a las características experimentales del estudio y tomando en cuenta las pendientes de las playas en los litorales mexicanos, se representó un perfil playero con pendiente 1:50 donde se desplantaron las secciones de rompeolas.
Secciones de rompeolas
Con base en el estado del arte, se propusieron 2 secciones de rompeolas superficiales de sección trapecial; se diseñaron con taludes 2:1 y 1,5:1 (lado mar) y 1,5:1 (lado puerto) constituidos por enrocamiento y elementos artificiales (dolos) en su coraza (pesos determinados con la fórmula de Hudson).
CRITERIOS DE DAÑO EN LA CORAZA
El daño de la coraza se caracteriza por el número de bloques desplazados del mismo o en algunos casos el área del perfil erosionado, en ambos casos relacionados con un estado del mar específico, como sugirió Iribarren en 1964 (Negro y Varela 2008).
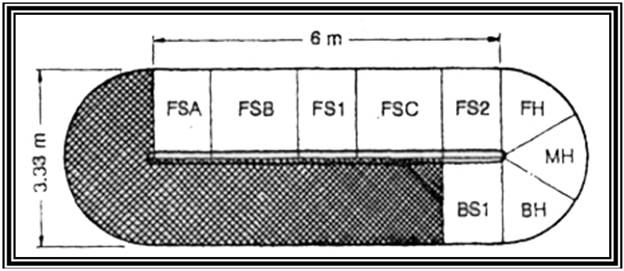
El daño expresado en términos de unidades desplazadas, normalmente se expresa como el porcentaje de unidades desplazadas respecto al número total de unidades de la coraza, o en una zona específica alrededor del nivel del mar conocido como zona activa (normalmente +/- Hs o +/- Dn) en una sección de rompeolas de anchura Dn, como Van der Meer (1992) sugirió, Burcharth (1993) para los dolos estableció que la zona activa a considerar era una franja alrededor del nivel del mar igual a +/- 6,5Dn (Dn = diámetro nominal del elemento de coraza). Esta dimensión relativa al lado equivalente y no a la altura, es posible que el lado equivalente esté relacionado con las condiciones de diseño (figura 1).
El daño relacionado con el área erosionada alrededor del nivel del mar fue definido por Iribarren (daño severo ocurría cuando la profundidad del área erosionada llegaba al diámetro nominal), por Hudson (porcentaje de volumen erosionado respecto al volumen inicial) y posteriormente, por Broderick (mediante la creación de una unidad adimensional para enrocamiento) (Negro y Varela 2008).
Para las secciones del cuerpo de los rompeolas a talud, el criterio del nivel de daño puede quedar definido como sigue:
Van der Meer (1992), definió la progresión del daño en tres diferentes etapas, en función del área erosionada (S) o del número de bloques desplazados en una sección del rompeolas:
Vidal y Losada (1994), definieron la progresión del daño en cuatro etapas:
Comienzo del daño. Porcentaje de piezas desplazadas igual al 5% y empiezan a verse algunos huecos en la primera capa de la coraza.
Daño de Iribarren. Cuando el daño se concentra en distintas áreas del rompeolas, eliminando la primera capa de bloques pudiendo extraer los bloques de la segunda capa. Este estado se sitúa en un área de bloques de 3 por 3 unidades. La coraza activa se sitúa en seis lados del cubo equivalente de forma aproximada.
Comienzo de destrucción. Algunas unidades de la capa secundaria desplazadas.
Destrucción. Cuando se extrae algún bloque de la capa secundaria, el material del núcleo queda expuesto al ataque de las olas.
Burcharth (1993), clasificaba el daño de la siguiente manera:
No daño. No hay desplazamiento de piezas.
Daño inicial. Algunas unidades desplazadas. En relación con el coeficiente de estabilidad de la fórmula de Hudson entre 0% y 5% de piezas desplazadas.
Daño intermedio. Desde moderado a severo. Con piezas desplazadas sin causar la exposición de la capa del núcleo.
Falla. Exposición de la capa de núcleo a la acción del oleaje.
Otros criterios establecidos en ensayos específicos en modelos físicos en morros de rompeolas a talud fueron:
Madrigal and Lozano (1992), definieron:
Berenguer and Baonza (1999) definen la progresión del daño en el morro en tres etapas:
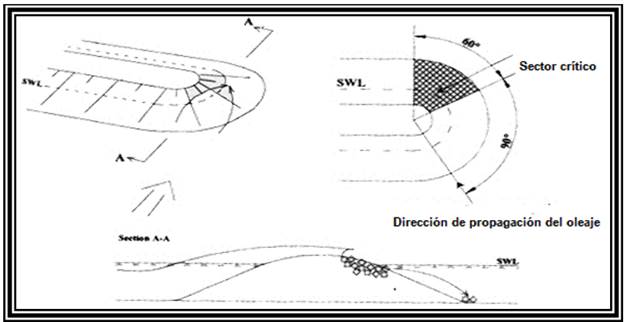
En las secciones del morro es posible usar estos criterios, pero el daño es diferente en función del sector del morro que se esté analizando. Para interpretar y evaluar el daño, es preciso dividirlo en sectores y calcular el daño relativo en cada uno de ellos en una zona predeterminada alrededor del nivel del mar. Jensen, Vidal y Madrigal (figura 2), dividieron el morro en 6 secciones diferentes; Matsumi (figura 3), dividió el morro en tres secciones (morro frontal, medio y trasero) al igual que Berenguer, aunque los tres sectores propuestos por este último fueran el S5, S6 y S7-S8 de Vidal (Negro y Varela 2008).
LOCALIZACIÓN DEL DAÑO EN LOS MORROS DE LOS ROMPEOLAS EN TALUD
El daño en el morro se produce, por una parte, por los efectos combinados de la concentración del impacto de la ola por refracción, difracción y asomeramiento de las olas alrededor del mismo y por otra parte, por la reducción del soporte de las piezas del manto a consecuencia de la desaparición de piezas desplazadas fuera de la sección no formando una berma de soporte (esto es cierto en el caso de rompeolas en aguas profundas, pero en el caso de profundidades reducidas las piezas desplazadas continúan formando parte del morro) (figura 4).
Jensen en 1984 sugirió que el sector más dañado en los morros de los rompeolas en talud era un área alrededor del nivel del mar en un sector que va desde que la ortogonal de las olas es tangente al cono y se extiende un poco más hacia delante de ese punto, entre 90° y 135° respecto a la normal del oleaje, y relativa a la principal alineación. La razón para ello es que, además del ataque del oleaje, una corriente generada por las olas rompientes causa un movimiento alrededor de la pendiente “swash”, que incrementa la velocidad del agua y genera una fuerza de succión y elevación más alta que en otras secciones (Negro y Varela 2008).
En los estudios de Vidal entre 1989 y 1991, se observó que era el área entre 90° y 120° donde el flujo del agua en el talud y la mayor esbeltez de las olas generaba una corriente hacia debajo de la sección que actuaba sobre las piezas del manto mayor que en el resto del morro. El comienzo del daño ocurría un poco antes que en el cuerpo, pero su progresión era muy rápida (Negro y Varela 2008).
Madrigal en 1992, analizó que con acrópodos y bloques paralepipédicos, el peor sector se encontraba entre 90° y 150° dada la velocidad y aceleración de agua en la zona. Después la progresión continuaba en las dos direcciones, a favor y en contra del oleaje (Negro y Varela 2008).
Matsumi en 1994, estudió un enrocamiento como coraza de muy escasa dimensión para analizar el daño en toda su progresión, encontró que la peor parte del morro era el sector 0° a 60°. La razón de este comportamiento inesperado (con respecto a los estudios anteriores) pudo ser el escaso tamaño de las rocas que implicaba que el rompeolas se comportaba como un rompeolas de berma en que efectivamente, la peor parte es la frontal, dado que otros sectores se alimentan de la misma (Negro y Varela 2008).
Berenguer en 1999, explicó que el daño sucede en el sector entre 90° y 150°, y que la progresión del mismo es contra el oleaje dado la pérdida de soporte de los bloques (Negro y Varela 2008).
MODELO FÍSICO HIDRÁULICO
Escala del modelo
En el estudio las fuerzas más importantes resultan ser las gravitacionales; por lo tanto el criterio de similitud entre prototipo y modelo es el que relaciona las fuerzas de inercia y gravitacionales (Número de Froude). En función de la ley de similitud de Froude y de la escala de líneas propuesta (1:40), se obtienen las escalas siguientes:
Arreglo del modelo
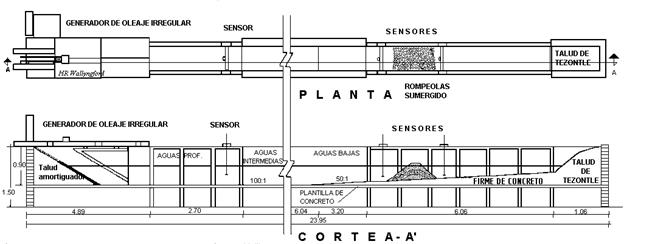
Los ensayos se llevaron a cabo en el canal de olas angosto del Laboratorio de Ingeniería Hidráulica de la Escuela Superior de Ingeniería y Arquitectura Unidad Zacatenco del Instituto Politécnico Nacional de México, con dimensiones de 24,50 m. longitud, 0,90 m. de altura y 0,66 m. de ancho (figura 5); el cual cuenta con un generador de oleaje irregular en uno de sus extremos, el que está dotado de una paleta generadora de oleaje de movimiento traslacional accionada mediante un gato hidráulico, cuyo control se efectúa por procedimientos electrónicos controlados por computadora. En el extremo contrario del canal se tiene un amortiguador para absorber la energía del oleaje, el cual limita la ocurrencia de reflexiones.
En el interior del canal se reprodujo el perfil del fondo marino frente al rompeolas en una longitud de 6,00 m., con una pendiente de 1:50 y un tramo de 9,00 m. de transición con pendiente 1:100 para poder ligar el fondo del canal con la pendiente del fondo marino; sobre el perfil del fondo se representaron las secciones de rompeolas a ensayar.
Con esta disposición se logró un tirante de agua frente al generador de olas de 0,50 m. (20 m. en prototipo) y un tirante al pie del rompeolas de 0,30 m. (12 m. en prototipo), referido al nivel de bajamar media inferior, tirante suficiente para un funcionamiento adecuado del generador de oleaje.
Instrumentación
Para la medición del oleaje a reproducir en los ensayos, se utilizaron dos sensores de oleaje de tipo resistivo. Las señales analógicas recabadas por los sensores se amplificaron a través de un ológrafo, que a su vez las envió a un convertidor de señales (analógico/digital) con el que cuenta el equipo de cómputo. Una vez digitalizadas fueron analizadas por el programa HR WAVES subrutina WARP (Beresford 1994b).
Construcción del modelo
Definida la disposición del modelo, se procedió a su construcción para lo cual se realizaron rellenos, compactados y firmes de concreto para obtener las pendientes del perfil marino a reproducir.
Ejecutados estos trabajos y con base en la escala del modelo, se calcularon los pesos de los materiales de enrocamiento de coraza y el volumen del material necesario para cada una de las estructuras. A continuación se determinaron los volúmenes de enrocamiento para la capa secundaria y el núcleo y finalmente se construyeron las secciones.
PROCEDIMIENTO EXPERIMENTAL
Programa de ensayos
Para la realización de la fase experimental, se programaron 8 señales de oleaje a reproducirse en los ensayos (generadas con el espectro de Pierson-Moskowitz en el programa HR WAVEGEN subrutina SEASTATE), las cuales se muestran en las tablas números 1 y 2 (Beresford 1994a):
Tabla 1 Programa de ensayos rompeolas coraza de enrocamiento
| Número de señal | Periodo (M) (s) | Periodo (P) (s) | Altura (M) (cm) | Altura (P) (m) | Intervalo de muestreo | Número de olas |
|---|---|---|---|---|---|---|
| 1 | 1,30 | 8,22 | 6,70 | 2,68 | 0,1624 | 2000 |
| 2 | 1,40 | 8,85 | 7,78 | 3,11 | 0,1749 | 2000 |
| 3 | 1,50 | 9,49 | 8,93 | 3,60 | 0,1875 | 2000 |
| 4 | 1,60 | 10,12 | 10,13 | 4,05 | 0,2000 | 2000 |
| 5 | 1,70 | 10,75 | 11,48 | 4,59 | 0,2125 | 2000 |
| 6 | 1,80 | 11,38 | 12,83 | 5,13 | 0,2246 | 2000 |
| 7 | 1,90 | 12,02 | 14,40 | 5,76 | 0,2381 | 2000 |
| 8 | 2,00 | 12,65 | 15,90 | 6,36 | 0,2502 | 2000 |
Tabla 2 Programa de ensayos rompeolas coraza de dolos
| Número de señal | Periodo (M) (s) | Periodo (P) (s) | Altura (M) (cm) | Altura (P) (m) | Intervalo de muestreo | Número de olas |
|---|---|---|---|---|---|---|
| 1 | 1,40 | 8,85 | 7,78 | 3,11 | 0,1749 | 2000 |
| 2 | 1,50 | 9,49 | 8,93 | 3,60 | 0,1875 | 2000 |
| 3 | 1,60 | 10,12 | 10,13 | 4,05 | 0,2000 | 2000 |
| 4 | 1,70 | 10,75 | 11,48 | 4,59 | 0,2125 | 2000 |
| 5 | 1,80 | 11,38 | 12,83 | 5,13 | 0,2246 | 2000 |
| 6 | 1,90 | 12,02 | 14,40 | 5,76 | 0,2381 | 2000 |
| 7 | 2,00 | 12,65 | 15,90 | 6,36 | 0,2502 | 2000 |
| 8 | 2,10 | 13,28 | 17,63 | 7,05 | 0,2635 | 2000 |
CONDICIONES Y PROCEDIMIENTO DE LOS ENSAYOS
Condiciones de los ensayos
Se utiliza el espectro de Pierson-Moskowitz para generar las señales de oleaje.
En los ensayos para medir la reflexión del oleaje se reprodujo oleaje en tiempo suficiente para que el equipo realice la medición (variable).
En todos los ensayos se mide el oleaje en dos puntos diferentes (al pie del generador de oleaje y al pie de los rompeolas).
Procedimiento de los ensayos
Ensayos para obtener el coeficiente de reflexión:
Se colocan tres sensores de oleaje a una distancia mayor de una longitud de ola, tanto del generador como de la estructura y separados entre sí de acuerdo con el periodo del oleaje.
Se reproduce oleaje y se mide la energía de ola incidente y reflejada en la estructura por cada uno de los sensores de oleaje.
Se calcula el coeficiente de reflexión, promediando las energías del oleaje incidente y reflejado (programa HR WAVES subrutina REFLECTION) (Beresford 1994b).
Ensayos para medir el daño en las estructuras:
Se genera oleaje para cada uno de los ensayos, en tiempo suficiente para tener una incidencia de 2000 olas sobre la estructura en prueba y un total de 16000 olas por serie.
Con base en los datos de oleaje transmitidos por los sensores al ológrafo y de éste al equipo de cómputo, se calculan las alturas y periodos de ola significante para cada ensayo.
Se miden los daños en las estructuras, siendo éstos acumulativos (Melby 1999).
PRESENTACIÓN DE LA INFORMACIÓN EXPERIMENTAL
En las tablas 3 y 4, se muestran los resultados de la mediciones de los parámetros de daño para las dos estructuras ensayadas y los aportados por los criterios de daño de Van der Meer, Broderick, Losada y Burcharth y Liu (Burcharth et al. 2000).
Tabla 3 Ensayos del daño sobre el rompeolas con coraza de enrocamiento
| Señal | Número de rocas | Rocas desplazadas | Daño (%) | Diám. medio | Área erosionada |
Parámetro Daño (S) |
Parámetro de daño (S) Van der Meer |
Parámetro de daño (S) Broderick |
Parámetro de daño (S) Losada |
||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 927 | 21 | 2,27 | 1,1432 | 0,0000 | 0,0000 | 0,3747 | Inicio de daño | S<2 | Inicio de daño | S<2 |
| 2 | 927 | 26 | 2,80 | 1,1432 | 0,0000 | 0,0000 | 1,1175 | ||||
| 3 | 927 | 26 | 2,80 | 1,1432 | 0,0000 | 0,0000 | 2,9226 | ||||
| 4 | 927 | 33 | 3,56 | 1,1432 | 1,7600 | 1,3466 | 5,1356 | ||||
| 5 | 927 | 35 | 3,78 | 1,1432 | 3,4304 | 2,6247 | 9,5654 | Daño moderado | 2<S<8 | Daño de Iribarren | 2<S<8 |
| 6 | 927 | 39 | 4,21 | 1,1432 | 7,7782 | 5,9513 | 14,5904 | ||||
| 7 | 927 | 70 | 7,55 | 1,1432 | 15,3600 | 11,7524 | 21,7499 | Capa sec. visible | S>8 | Inicio dest. | 8<S<14 |
| 8 | 927 | 101 | 10,90 | 1,1432 | 21,3600 | 16,3432 | 27,9250 | Colapso | S>14 | ||
Tabla 4 Ensayos del daño sobre el rompeolas con coraza de dolos
| Señal | Número de dolos | Dolos desplazados | Daño (%) | Diámetro medio | Área erosionada |
Parámetro Daño (S) |
Parámetro de daño (S) Burcharth y Liu |
|---|---|---|---|---|---|---|---|
| 1 | 949 | 18 | 1,90 | 1,0455 | 0,0000 | 0,0000 | Inicio de daño |
| 2 | 949 | 22 | 2,32 | 1,0455 | 0,0000 | 0,0000 | |
| 3 | 949 | 25 | 2,63 | 1,0455 | 0,0000 | 0,0000 | |
| 4 | 949 | 27 | 2,85 | 1,0455 | 1,0048 | 0,9192 | |
| 5 | 949 | 45 | 4,74 | 1,0455 | 1,5819 | 1,4472 | |
| 6 | 949 | 49 | 5,16 | 1,0455 | 3,4607 | 3,1659 | |
| 7 | 949 | 54 | 5,69 | 1,0455 | 7,4401 | 6,8064 | |
| 8 | 949 | 59 | 6,22 | 1,0455 | 14,6021 | 13,3584 | Capa sec. visible |
ANÁLISIS DE RESULTADOS
Realizado el análisis de los datos producto de los ensayos, se desarrollaron unas gráficas (figuras 6 y 7), en las cuales se relacionaron los datos aportados por el estudio.
CONCLUSIONES
Una vez procesada y analizada la información obtenida de los ensayos, se procedió a formular las conclusiones con base en las tablas presentadas en el apartado anterior.
Resultados de la evolución del daño en el rompeolas de enrocamiento:
De la tabla 3 se puede observar que para el talud 2:1 el inicio de daño se presenta cuando S = 2 (de 1 a 5 % de daño).
Que la falla total para el rompeolas (capa secundaria visible), se presenta cuando S = 16,34 (10,90 % de daño).
Los parámetros de daño medidos con respecto a los propuestos por van der Meer, presentan una gran variación (tabla 3).
Los parámetros de daño medidos con respecto a los propuestos por Broderick, se ajustan adecuadamente en la parte de inicio de daño y daño moderado, y divergen en el daño total (tabla 3).
Los parámetros de daño medidos con respecto a los propuestos por Losada, se ajustan adecuadamente en los casos de inicio de daño, daño de Iribarren, inicio de destrucción y colapso, siendo por lo tanto estos factores los más adecuados para la evaluación del daño en un rompeolas con coraza de enrocamiento (tabla 3).
Los daños considerados para la estructura solo son aplicables para capas de coraza constituidas por dos elementos de espesor de enrocamiento.
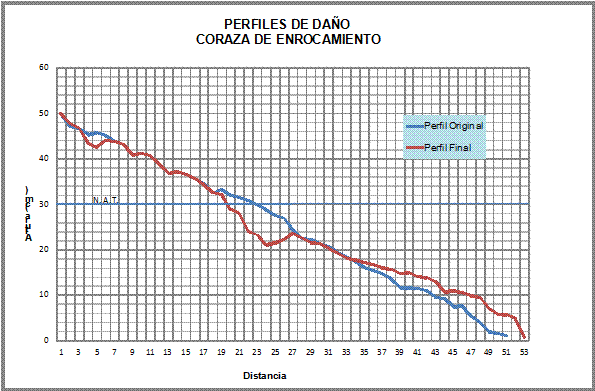
De la figura 6 se puede observar que en el perfil el área de daño del talud se presenta en la zona inferior inmediata al nivel de aguas tranquilas (N. A. T.).
En la figura anterior también se denota que el material de enrocamiento desplazado se restablece en la parte inferior del talud.
Resultados de la evolución del daño en rompeolas de dolos:
De la tabla 4 se puede observar que para el talud 1,5:1, el inicio de daño se presenta cuando S = 1 (2,85 % de daño).
Así también que la falla total para el rompeolas (capa secundaria visible), se presenta cuando S = 13,36 (6,22 % de daño).
Los parámetros de daño medidos con respecto a los propuestos por Burcharth y Liu, se ajustan adecuadamente en el apartado de inicio de daño, pero divergen en el daño total (capa secundaria visible). Por lo anterior este método no se considera adecuado para la evaluación de las condiciones de daño de un rompeolas con coraza de dolos (tabla 4).
Que los daños considerados para la estructura solo son aplicables para capas de coraza constituidas por dos elementos de dolos de espesor.
De la figura 7 se puede apreciar que en el perfil el área de daño del talud se presenta en la zona inferior inmediata al nivel de aguas tranquilas (N. A. T.).
En la figura anterior se puede observar que los dolos desplazados se reubicaron en la parte inferior del talud.
RECOMENDACIONES
Se considera pertinente establecer las siguientes:
Sería conveniente continuar el estudio en modelo físico reducido, implementando nuevas estructuras en las que se presenten otros elementos de coraza de concreto, para ampliar la gama de pruebas.
Ensayar con mayor número de taludes de las estructuras.
Llevar los ensayos hasta la falla total de las estructuras.