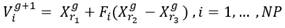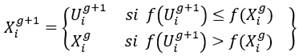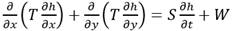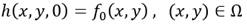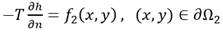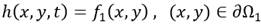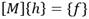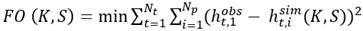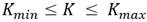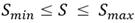Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
La complejidad de los medios geológicos, en especial las formaciones acuíferas, una de las principales fuentes portadoras del recurso elemental para la vida (el agua), han provocado y favorecido el desarrollo de modelos numéricos. Estos modelos permiten a los especialistas dotarse de una herramienta capaz de simular y estimar el comportamiento de los sistemas acuíferos ante diferentes acciones, ya sean provocadas por el hombre o por la misma naturaleza (Ramos 2016).
El problema que surge cuando se conocen las propiedades hidrogeológicas, las condiciones iniciales, las condiciones de frontera del acuífero y se desea determinar la distribución espacial y temporal de los niveles del agua subterránea se conoce como problema directo o de simulación. Sin embargo, el desarrollo de herramientas de simulación no ha ido convenientemente acompañado de un desarrollo paralelo de las herramientas de estimación de parámetros hidrogeológicos. La obtención de los valores de los parámetros hidrogeológicos de un acuífero, conductividad hidráulica (K) y coeficiente de almacenamiento (S) a partir de datos de niveles piezométricos se conoce como el problema inverso de la hidrología subterránea.
Durante la estimación de parámetros, el proceso de modificarlos continuamente hasta que se logre una buena coincidencia entre los valores simulados y observados se denomina calibración. Este proceso puede realizarse de forma manual mediante un proceso de prueba y error, o de forma automática mediante algoritmos de optimización, donde los algoritmos metaheurísticos han alcanzado un gran auge en los últimos tiempos.
Las técnicas metaheurísticas representan los algoritmos de optimización más generales. La mayor parte de los algoritmos metaheurísticos están inspirados en comportamientos que se llevan a cabo en la naturaleza, teniendo en cuenta las principales características de los sistemas biológicos.
Los algoritmos genéticos constituyen una de las variantes más populares a la hora de elegir un algoritmo metaheurístico (Mallepedi et al. 2011). Fueron desarrollados por John H. Holland a principios de los 60’. Las principales ventajas que presentan es que son capaces de explorar el espacio de soluciones en múltiples direcciones a la vez, además de resolver problemas altamente no lineales y complejos y tienen el potencial para acoplarse con otras técnicas de búsqueda-optimización (Marczyk 2004).
En Cuba, con la creación del modelo de simulación de flujo del agua subterránea AQÜIMPE (Martínez 1989), el problema inverso ha sido resuelto, inicialmente, mediante la calibración manual, sin embargo, (Mesa 2004) resuelve el problema inverso aplicando un algoritmo genético de convergencia global llamado Shuffled Complex Evolution (SCE) en la tecnología AQÜIMPE. Se han acoplado, además, al modelo de flujo AQÜIMPE, luego de su migración al software MATLAB y de la creación de la herramienta META-AQÜIMPE técnicas metaheurísticas novedosas. Sin embargo, la complejidad del propio problema inverso de la hidrogeología hace imposible definir qué algoritmo es el más adecuado para encontrar la solución óptima, es por eso que enriquecer la tecnología AQÜIMPE con nuevas técnicas metaheurísticas es útil y necesario si se quieren evaluar y administrar con rigor los recursos hidráulicos subterráneos.
En la presente contribución se discute un modelo de calibración automática que utiliza como técnica de búsqueda el algoritmo evolución diferencial (DE, por sus siglas en inglés) acoplado al modelo de flujo AQÜIMPE en el entorno de Matlab (META-AQÜIMPE), este modelo se aplica para el caso de un acuífero real.
Algoritmo evolución diferencial
El algoritmo evolución diferencial (DE) introducido por (Storn y Price 1997), es un algoritmo basado en poblaciones que utiliza los operadores básicos de los algoritmos genéticos: mutación, cruzamiento y selección. Las razones por las que los investigadores encuentran a DE como una poderosa herramienta de optimización son (Das and Suganthan 2011): (a) comparado con la mayoría de los algoritmos evolutivos, es mucho más simple y noble de implementar, (b) a pesar de su simplicidad exhibe buenos resultados en problemas multimodales complejos, (c) el número de parámetros heurísticos que posee es muy pequeño y sus efectos en el rendimiento del algoritmo han sido bien estudiados.
DE emplea un método de búsqueda paralelo que utiliza un número de agentes en un espacio de búsqueda. Las posiciones de los agentes son inicializadas aleatoriamente. Cada agente representa un punto en el espacio, de coordenadas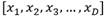 
, donde D representa la dimensión del problema. Estos agentes constituyen vectores de posición, de orden (NP x D), que se denotan según la forma 
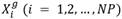, donde g es el contador de generaciones y NP es el número de agentes que integran la población. Cada agente constituye una solución del problema de optimización.
Mutación
En DE, la mutación se evidencia a partir de la construcción del denominado ‘‘vector mutado’’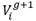 
(de iguales dimensiones del vector 
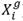), el cual se inicializa normalmente con valores nulos. Este vector se construye a partir de la adición de una diferencia ponderada entre dos agentes de la población con un tercero, tal como se muestra en la ecuación (1).
(1)
donde: r1, r2, r3, son subíndices diferentes escogidos aleatoriamente en el intervalo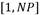 
en cada generación, en los cuales no se incluye el subíndice del agente que se muta. F es un vector, de orden (1 x NP) denominado factor de escala, el cual se distribuye uniformemente en el espacio 
.
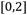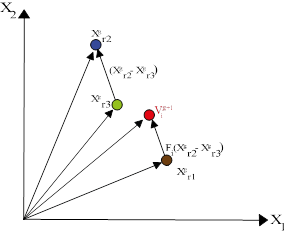
Este vector controla la amplificación de la variación diferencial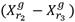 
(Storn and Price 1997). La ecuación de mutación se aplica para cada agente del proceso. La ecuación (1) se encuentra dentro de las estrategias de mutación más aplicadas, esta estrategia se conoce en la literatura con la notación DE/rand/1/bin, propuesto por (Storn and Price 1997) para identificar que el agente que se muta se escoge de manera aleatoria en la población y que se realiza un cruzamiento binomial. En la figura 1 se muestra la representación gráfica de la ecuación (1) en un espacio bidimensional.
Cruzamiento
Según (Feoktistov 2006), el rol principal del cruzamiento es mezclar la información aportada por el agente o vector de posición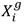 
y el vector mutado 
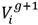(muchas veces llamados vector ‘‘padre’’ y vector ‘‘donador’’ respectivamente) para mejorar la diversidad de la población y poder explorar regiones más prometedoras.
En este sentido, es necesaria la construcción de un tercer vector, el vector 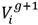, denominado vector de prueba, el cual se inicializa con valores nulos y su función es retener parte de la información de los vectores 
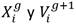. Su construcción se realiza componente a componente de acuerdo con la ecuación (2):
(2)
donde: rand es un vector, de orden (1 x D) distribuido uniformemente en el espacio 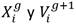se denomina constante de cruzamiento y viene dado por un valor constante del espacio 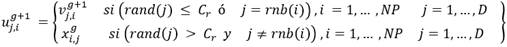determinado por el usuario, rnb representa un subíndice escogido aleatoriamente en el espacio 
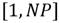que asegura que el vector de prueba 
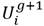contenga al menos una componente del vector mutado 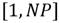son componentes de los vectores de prueba, mutación y posición respectivamente. En la figura 2 se muestra un posible esquema de cruzamiento para un caso de dimensión D = 7.
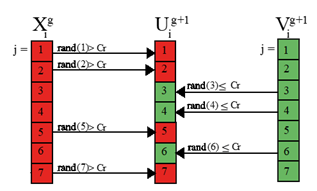
Fig. 2 Representación de un posible esquema de cruzamiento para el caso D = 7. (Modificada de Storn and Price 1997)
Selección
Para decidir que vector pasa a la siguiente generación, el vector de prueba 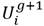y el vector de posición 
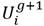son evaluados en la función objetivo y comparados utilizando el criterio de la codicia de acuerdo a la siguiente regla:
(3)
MODELO DIRECTO
El modelo matemático AQÜIMPE (Martínez 1989), resuelve la ecuación diferencial parcial de segundo orden, de tipo parabólica, que gobierna el flujo bidimensional, impermanente, lineal y confinado en un medio poroso con término fuente-sumidero dada por la ecuación (4):
(4)
sujeta a la siguiente condición inicial y condiciones de borde que se muestran a continuación (5), (6) (7):
(5)
(6)
(7)
donde: h es la carga hidráulica, T la transmisividad del acuífero, S coeficiente de almacenamiento del acuífero, W es el término fuente o sumidero, t el tiempo, x, y son las variables espaciales, ( región de flujo, ∂( contorno de la región de flujo (∂( = ∂Ω1 ∪∂Ω2), ∂/∂n derivada normal al contorno, y f 0 , f 1 , f 2 son funciones conocidas.
AQÜIMPE resuelve la ecuación (4) mediante el método del elemento finito (MEF) con triángulo cuadrático como elemento de discretización, utilizando la aproximación de Galërkin, permitiendo obtener la carga hidráulica en función de las variables espaciales (x, y) y del tiempo (t) (Cabrera y Dilla 2011). Al aplicar el MEF la ecuación (4) se transforma en un sistema matricial de ecuaciones lineales, que cuando se trata de un acuífero confinado, el problema consiste en resolver k veces el sistema de ecuaciones lineales mostrado en la ecuación (8) (Cabrera y Dilla 2011).
(8)
donde: M es una matriz simétrica cuadrada, de orden (n x n) (n es el número de nodos), en la que cada fila está asociada con uno de los nodos de la malla. Lo mismo sucede con las columnas. En el vector h se guardan las variables a calcular en cada tiempo k y f es el vector de los términos independientes donde se almacena el efecto de los caudales extraídos e incorporados al modelo en cada nodo (Cabrera y Dilla 2011). Dada la simetría de la matriz M, el sistema de ecuaciones lineales descrito en (8) se resuelve mediante el método conocido como método de la raíz cuadrada o de Choleski (Cabrera 2007).
MODELO INVERSO
La herramienta META-AQÜIMPE emplea la ecuación (9) como función objetivo (FO) del problema de optimización sujeta a las restricciones que se muestran en las ecuaciones (10) y (11). Esta función objetivo minimiza las diferencias entre los niveles observados y simulados del acuífero, donde N p es el número de pozos de observación, Nt es el número de tiempos, h obs es el nivel observado en los pozos de observación, h sim es el nivel simulado por el modelo, K min y K max representan los valores mínimos y máximos de la conductividad hidráulica y S min y S max representan los valores mínimos y máximos del coeficiente de almacenamiento.
(9)
(10)
(11)
El módulo que se propone en este trabajo integra a la herramienta META-AQÜIMPE el algoritmo DE para realizar la calibración automática de modelos de acuíferos. Este acople se realiza en el entorno de MATLAB. En la figura 3 se muestra un diagrama de flujo con las principales etapas de este módulo.
En (Verdés 2018) se demuestra a partir de la calibración del modelo de un acuífero hipotético, que los parámetros heurísticos NP = 10 y C r = 0.8 garantizan un buen rendimiento del algoritmo DE, estos parámetros son los utilizados para la calibración del caso de estudio.
Fig. 3 Diagrama de flujo de la herramienta META - AQÜIMPE con el algoritmo evolución diferencial acoplado
MODELO CONCEPTUAL
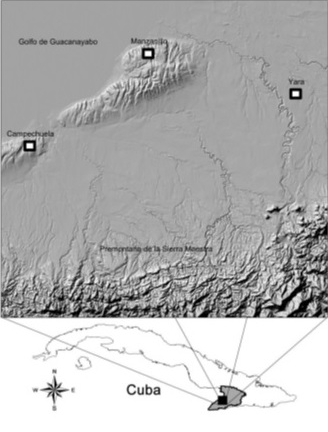
La zona de estudio (sector Cuentas Claras, SCC), ocupa un área aproximada de 1560 km², comprendiendo a los municipios Manzanillo, Campechuela y Yara, pertenecientes a la provincia Granma, Cuba.
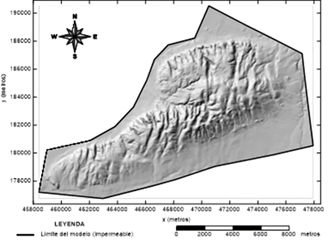
Esta zona limita al norte con el Golfo de Guacanayabo, al sur con las premontañas de la Sierra Maestra, al este con el municipio Yara y al oeste con el municipio Campechuela (figura 4). (Blanco et. al 2010).
La recarga del acuífero Cuentas Claras se produce fundamentalmente en las premontañas de la Sierra Maestra ubicadas al sur del sector. Sin embargo, los resultados de los estudios geológicos y geofísicos, sugieren que el aporte de la recarga de la zona montañosa al sector Cuentas Claras proviene de fallas geológicas bajo este, por lo que el flujo debe ser vertical con significativas componentes de velocidad.
En el modelo conceptual se excluye dicha zona y se introduce el aporte de la montaña indirectamente en el sector como una lámina adicional a la lámina de la precipitación que ocurre sobre Cuentas Claras.
Límites y condiciones de contorno del SCC
A partir de los estudios hidrogeológicos, geofísicos, geológicos e hidrológicos realizados en la zona de estudio, (Ramos 2012) procedió a definir el área del modelo y sus fronteras como se muestra en la figura 5.
En el área de estudio se encuentran un total de 51 pozos de explotación controlados por tres organismos: la Industria con 11 pozos, el Ministerio de la Agricultura (MINAGRI) con 12 pozos y el Poder Popular, por medio del acueducto, con 28 pozos.
El área cuenta con una red de 8 pozos de observación con mediciones desde enero de 1991 hasta noviembre de 2011, pero de este período solamente en los años de 1997 al 2000, los registros de 7 de ellos tienen observaciones mensuales.
Discretización de la zona de estudio
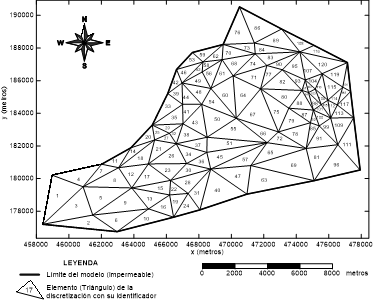
Para la creación de la malla de triángulos se utilizó la herramienta SIG AQTRIGEO. En la figura 6 se muestra la discretización del área del Sector Cuentas Claras. La malla mostrada está compuesta por 121 elementos (triángulos) y 264 nodos (vértices y centros de cada lado de los triángulos).
Grupos de infiltración y propiedades hidrogeológicas
Atendiendo a las características hidrofísicas de los distintos tipos de suelos del área en cuestión, a la asignación de la recarga por zonas mediante los polígonos de Thiessen y a la discretización del área a modelar, (Ramos 2012) definió un conjunto de 8 grupos de infiltración, además decide agrupar los triángulos en 10 grupos o zonas de propiedades hidrogeológicas atendiendo a la información aportada por la geología y la geofísica. En la figura 7 se muestra la distribución de estos grupos sobre el área del SCC.
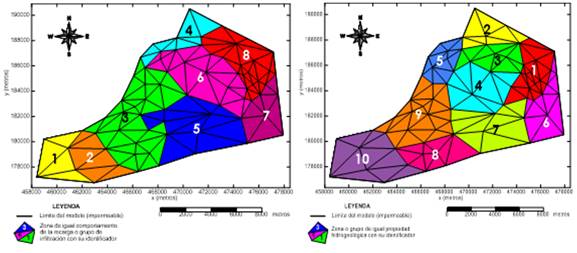
Fig. 7 Distribución de los grupos de infiltración (izquierda) y grupos de propiedades hidrogeológicas (derecha)
Estado inicial del acuífero
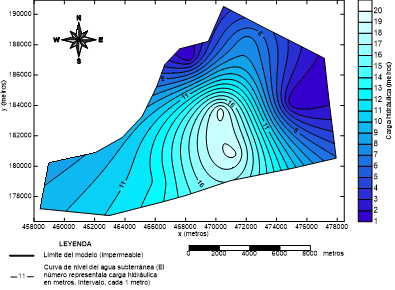
Con los datos de niveles en los pozos de observación del mes agosto del año 1998, se realiza una interpolación con la ayuda de la herramienta Surfer 13, utilizando el método de Kriging, mediante el cual se obtiene el mapa de hidroisohipsas que se muestra en la figura 8.
Calibración del modelo
Para realizar la calibración del modelo del SCC, se utiliza la herramienta META-AQÜIMPE con DE como algoritmo de optimización. En todas las ejecuciones se emplean los valores de los parámetros heurísticos NP = 10 y C r = 0.8. El intervalo donde se calibrarán las propiedades se muestra en la tabla 1.
Tabla 1 Límites del intervalo de búsqueda de los parámetros (establecido por Ramos 2012)
| Grupos de Propiedades | Intervalo de propiedades | |||
|---|---|---|---|---|
| Transmisividad (m2/d) | Coeficiente de almacenamiento | |||
| Mínimo | Máximo | Mínimo | Máximo | |
| 1-10 | 10 | 5000 | 0,001 | 0,1 |
En la tabla 2 se muestra el resultado de algunas de las 15 ejecuciones realizadas con el algoritmo DE durante el proceso de calibración. En cada ejecución se realizaron 10000 evaluaciones de la función objetivo
Tabla 2 Resultados de la calibración del modelo del SCC
| Ejecuciones | Valor de la FO |
|---|---|
| 1 | 52,50 |
| 3 | 41,74 |
| 5 | 70,11 |
| 7 | 61,80 |
| 10 | 52,03 |
| 11 | 64,00 |
| 12 | 55,81 |
| 13 | 40,65 |
| 14 | 43,75 |
| 15 | 57,75 |
| Promedio | 55,10 |
El mejor resultado de la tabla 2 se obtiene en la ejecución 13, donde se alcanza el menor valor de la FO.
El algoritmo presentó un ritmo de convergencia acelerado durante las 100 primeras generaciones (figura 9), esta característica estuvo reflejada en cada una de las ejecuciones que se realizaron y los tiempos de cómputo necesarios para realizar cada ejecución estuvieron cercanos a los 25 minutos.
DE logra disminuir considerablemente el valor de la FO en las etapas tempranas del proceso de búsqueda, sin embargo, a partir de 500 generaciones tuvo una tendencia general al estancamiento en cada ejecución, por lo que no es recomendable establecer grandes valores de evaluaciones de la función objetivo como criterio de parada de este algoritmo, se recomienda hasta 10000 evaluaciones de la función objetivo. Los valores de las propiedades calibradas pueden encontrarse en (Verdes 2018).
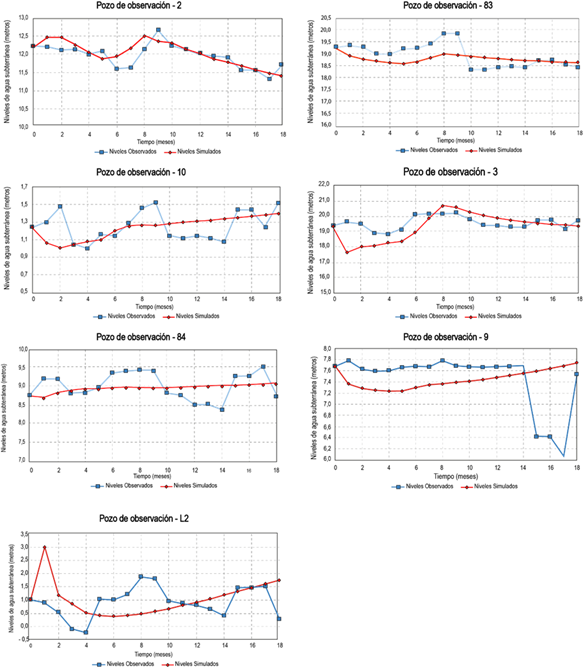
A continuación, se realiza una comparación entre los niveles simulados y observados en cada pozo de observación, en la ejecución 13 (figura 10).
Conclusiones
Mediante el empleo de la herramienta META-AQÜIMPE con el algoritmo DE acoplado para calibrar modelos de acuíferos y los parámetros heurísticos que garantizan un buen rendimiento del algoritmo, se obtienen nuevos valores para las propiedades hidrogeológicas representativas del modelo del sector Cuentas Claras, además se redujo considerablemente el tiempo de cómputo y el número de evaluaciones de la función objetivo.
El algoritmo DE presenta un ritmo de convergencia acelerado en sus primeras 100 generaciones, donde logra reducir el valor de la función objetivo en pocas evaluaciones. Esta característica resulta ser muy beneficiosa, ya que en el proceso de calibración de modelos de acuíferos se realizan gran cantidad de evaluaciones de la función objetivo y es donde más tiempo se emplea. Sin embargo, demostró que pasadas las 500 generaciones es propenso al estancamiento, por lo que no se justifica un número elevado de evaluaciones de la función objetivo como criterio de parada del algoritmo.
Se demuestra que DE con los parámetros heurísticos obtenidos se pueden calibrar propiedades hidrogeológicas empleando pocas evaluaciones. Estas propiedades garantizan un comportamiento hidrodinámico del modelo similar al observado.
