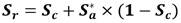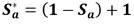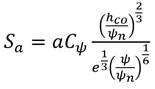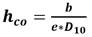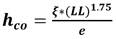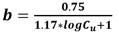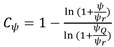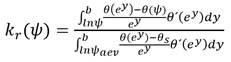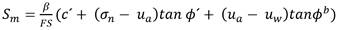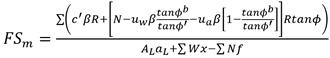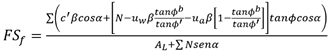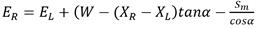Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
El deslizamiento de los taludes constituye una de las principales causas de falla de presas de tierra en el mundo. Debido a los efectos del cambio climático, los ciclos de lluvia han sufrido alteraciones, alargando los períodos secos, y modificando el régimen de lluvia en cuanto a frecuencia, duración e intensidad (Fonseca et al., 2020). Las variantes que pueden ocasionar un deslizamiento de talud son varias, sin embargo, en los últimos años, una de las más importantes e influyentes es la acción de la lluvia, causando, en su mayoría, fallas no catastróficas, pero sí costosas en su reparación, en el talud aguas debajo de las presas de tierra (Malla and Kumar, 2021)
El diseño de una presa de tierra comprende disímiles parámetros que abarcan desde el tipo de sección transversal, el nivel de agua máximo, el ancho de la corona, la pendiente de los taludes aguas arriba y aguas abajo, hasta el sistema de drenaje a utilizar. La forma en la que serán evacuadas las aguas del interior del terraplén afecta significativamente la permeabilidad y el grado de saturación del suelo, parámetros ambos fundamentales para el cálculo del factor de seguridad (FS) de los taludes al incluirse en el análisis la mecánica de suelos no saturados (Flores et al., 2019). El valor del FS expresa la magnitud en que puede reducirse la resistencia a cortante del suelo para que se produzca el deslizamiento a lo largo de la superficie más desfavorable (Armas y Horta, 1987).
Debido a la infiltración de la lluvia, pueden ocurrir varios tipos de fallas de taludes, dependiendo de su morfología, las curvas características del suelo y la resistencia al corte involucrada. Se han revelado vínculos complicados entre las circunstancias de lluvia, la presión intersticial del agua, la resistencia del suelo, las variables de seguridad y las tasas de movimiento (Lee et al., 2021). Al infiltrarse, las precipitaciones son una de las principales causas de los deslizamientos de taludes que cobran la vida de muchas personas y provocan importantes pérdidas económicas en todo el mundo. El agua de lluvia que no logra infiltrarse en el suelo se convierte en escorrentía y fluye cuesta abajo. Ambos escenarios (infiltración de lluvia y escorrentía) contribuyen a la pérdida de succión en el suelo, lo que resulta en la falla del talud.
Caracterización de los suelos no saturados
Se denomina suelo no saturado, a aquellos en los cuales los vacíos están ocupados parcialmente por agua y aire (Tristá, 2015). En el presente estudio se tuvieron en cuenta características fundamentales de los suelos parcialmente saturados, tales como la succión matricial, conductividad hidráulica y contenido volumétrico de agua. Estas características fueron introducidas al modelo a partir de las curvas representativas de los suelos.
La succión matricial se define como la presión isotrópica ejercida por el agua de los poros para absorber más agua. Esta se determina como la diferencia de presiones entre el aire y el agua de los poros (Fredlund and Rahardjo, 1993). El contenido volumétrico de agua se interpreta como el porciento de agua presente en una muestra de suelo, pudiéndose expresar en términos gravimétricos o volumétricos (Fredlund and Rahardjo, 1993). En términos del contenido de agua, es importante destacar que la capacidad de almacenamiento es función del índice de poros del suelo y del grado de saturación; de la lluvia que se precipita sobre la superficie del terreno, una parte importante se infiltra en el suelo, dando inicio al llenado de los poros vacíos entre las partículas del suelo.
Curva característica y de conductividad hidráulica de los suelos no saturados
En la presente investigación se determinó la curva característica de los suelos empleando el método de Aubertin (2003). Este método predice la función de contenido volumétrico de agua utilizando propiedades básicas del material, tales como la granulométrica de los suelos, se desarrolla considerando el tamaño, la forma de las partículas y la porosidad propias del material.
Para obtener el grado de saturación se relacionan dos componentes fundamentales del suelo, el primero tiene en cuenta las fuerzas capilares que existen a presiones intersticiales negativas relativamente pequeñas y el segundo, considera que la cantidad de agua es principalmente una función de la adhesión. El grado de saturación determinado en base a los componentes capilar y adhesivo se muestra en la ecuación 1.
(1)
Dónde S r es el grado de saturación, S c es el grado de saturación debido a las fuerzas capilares y S a * es el grado acotado de saturación debido a la adhesión (S a ), calculado según la ecuación 2.
(2)
El componente adhesivo es un valor acotado, ya que es posible que a bajas succiones el valor de 𝑆𝑎 sea mayor que 1; por lo que el valor acotado asegura que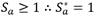, si 
y si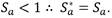 
El componente adhesivo está asociado con una película delgada de agua que cubre la superficie del grano y depende de las propiedades básicas del material, como son: la presión negativa del agua intersticial en el suelo, el tamaño de las partículas, el coeficiente de forma y la porosidad, siendo determinado por la ecuación 3.
(3)
Dónde a es el parámetro de ajuste de la curva, considerado como constante 7×10-4 para suelos cohesivos, ψ es la succión, ψ n es el término de la succión introducido para asegurar un componente adimensional, 𝑒 es la relación de vacíos del suelo y h co es la elevación capilar media (cm) determinada para suelos capilares, obtenida mediante la ecuación 4 o la ecuación 5, según los datos de los que se disponga.
(4)
(5)
Siendo D 10 (cm) el diámetro efectivo correspondiente al 10% de la curva granulométrica, LL es el Límite Líquido (%), y ξ es una constante igual a 402,2 cm2. Para obtener el parámetro asociado al coeficiente de uniformidad para suelos granulares (b), se emplea la ecuación 6.
(6)
Donde C u es el coeficiente de uniformidad (adimensional) y C ψ es el coeficiente de corrección que permite disminuir el contenido de agua para succiones altas, basado en el propuesto por Fredlund et al. (1994) obtenido mediante la ecuación 7.
(7)
Siendo ψ 0 la succión inicial, considerada igual a 10-7 cm, expresada en términos de columna de agua y ψ r la succión correspondiente al contenido de agua residual en cuyo punto un aumento en la succión no eliminará más agua del suelo, y está dado por la ecuación 8.
(8)
Este método es uno de los que se encuentra disponible para implementar en el GeoStudio (2018), paquete integral de herramientas informáticas diseñado para modelar la estabilidad de pendientes, la deformación del suelo y la transferencia de calor y masa en suelo y roca. Este es el único método disponible en el programa que depende de los parámetros de la curva granulométrica de los suelos para obtener el contenido de agua volumétrico y la succión de los mismos.
Con respecto a la curva de conductividad hidráulica, a diferencia de un suelo saturado, el cual mantiene una conductividad hidráulica constante; en un suelo no saturado, la conductividad hidráulica es variable, y depende del contenido de agua o estado de succiones que exista en el suelo (Mendoza, 2018). En términos del contenido de agua es importante destacar que la capacidad de almacenamiento es función del índice de poros del suelo y del grado de saturación (Fredlund and Rahardjo, 1993). La función de conductividad hidráulica correspondiente al modelo de Fredlund et al. (1994) se muestra en la ecuación 9.
(9)
Donde k r (ψ) es la función de conductividad hidráulica respecto a la succión, b es el límite superior de integración, considerado como ln(1 000 000), ψ es la succión del suelo, e es el número natural de Euler (2,71828), 𝑦 es una variable ficticia de integración que representa el logaritmo de la succión, θ´ es la derivada del modelo que ajusta la curva característica del suelo, θ(ψ) es la curva característica del suelo, ψ aev es el valor de entrada de aire al suelo y θ s es el contenido volumétrico de agua del suelo.
Estabilidad de taludes empleando el método de morgenstern-price
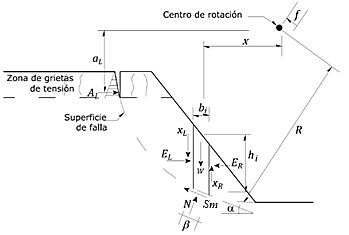
En los Métodos de Equilibrio Límite (MEL), se evalúa el talud en su estado de falla a partir del análisis de dos ecuaciones generales que rigen el FS. Los elementos de la estática, empleados para determinarlo son: la sumatoria de fuerzas horizontales y verticales, y la sumatoria de momentos. Estos requerimientos complican la solución del método convirtiéndolo en un problema indeterminado (Morgenstern and Price, 1965). La geometría, en conjunto con el criterio de falla, y asumir la dirección y magnitud de las fuerzas entre dovelas, son requerimientos para que el MEL se convierta en un problema determinado. En términos generales, el análisis de estabilidad de taludes con el MEL consiste en dividir la masa del suelo en dovelas delimitadas por la superficie de falla y la superficie del terreno, como se muestra en la figura 1.
(Fredlund and Rahardjo, 1993)Figura 1 Fuerzas actuantes en una dovela con superficie de falla circular
Donde W es el peso total de una dovela de ancho b y altura h, N es la fuerza normal total sobre la base de la dovela, 𝑆𝑚 es la fuerza cortante en la base de la dovela, 𝐸 es la fuerza horizontal normal entre dovelas (los subíndices L y R designan el lado izquierdo o derecho de la dovela), 𝑋 es la fuerza cortante entre dovelas (L y R designan el lado izquierdo o derecho de la dovela), 𝑅 es el radio de la superficie circular de falla asociada con la fuerza cortante 𝑆𝑚, 𝑓 es la distancia perpendicular de la fuerza normal desde centro de rotación, 𝑥 es la distancia horizontal del centro de cada dovela al centro de rotación, ℎ𝑖 es la distancia vertical del centro de la base de cada dovela a la superficie del terreno, 𝛼 es el ángulo entre la tangente al centro de la base de cada dovela y la horizontal (cuando el ángulo se inclina en la misma dirección de la geometría del talud, 𝛼 es positivo y viceversa), 𝐴 es la resultante de la fuerza externa que produce el agua, 𝑎 es la distancia perpendicular de la resultante de la fuerza del agua al centro de rotación o al centro de momentos y 𝛽 es la longitud de la base de la dovela.
Según Fredlund and Rahardjo (1993) la fuerza cortante que actúa en la base de cada dovela se escribe a partir de la resistencia al corte para un suelo no saturado como se muestra en la ecuación 10.
(10)
Donde σn es la tensión normal en el centro de la base de una dovela. La fuerza normal en la base de la dovela se determina por la sumatoria de fuerzas en la dirección vertical como se muestra en la ecuación 11.
(11)
Para obtener el factor de seguridad se tiene una ecuación de momento (12) y una ecuación de fuerzas (13).
(12)
(13)
Donde ω es el ángulo de la carga puntual desde la horizontal. La interacción entre dovelas puede considerarse a partir de la ecuación 14.
(14)
Asimismo, esta ecuación plantea que la fuerza cortante (X) se relaciona con la fuerza normal (E) a partir de la función planteada por Morgenstern & Price (1965), y que se muestra en la ecuación 15.
(15)
Dónde f(x) es la función que describe la forma en cómo varía la relación X/E a lo largo de la superficie de deslizamiento y λ es una constante que representa el porcentaje de la función, f(x), usada para resolver las ecuaciones del factor de seguridad.
El método planteado por Morgenstern and Price (1965) satisface las condiciones de equilibrio de fuerzas y de momentos en cada dovela y presenta una alta flexibilidad para considerar la función que describe la fuerza interdovelas.
Construcción del modelo numérico
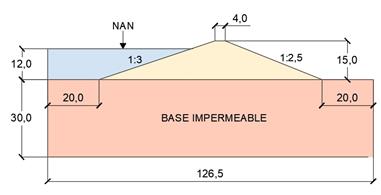
La geometría del modelo se definió a partir de un análisis de todas las presas existentes en Cuba. De las 242 presas de tierra construidas, 157 son homogéneas, de las que el 39,5% tiene hasta 15 metros de altura de cortina. La geometría del modelo numérico, a partir de las características de este tipo de presa, se muestra en la figura 2.
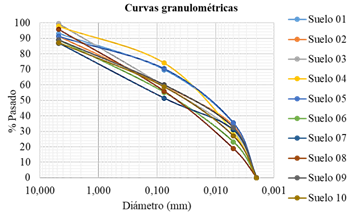
Para definir los materiales que conformarán los terraplenes de las presas de tierra se seleccionaron 10 suelos arcillosos con clasificación de arcilla de alta o baja compresibilidad (SUCS) según el Sistema Unificado de Clasificación de Suelos (SUCS). En todos los suelos se consideró una relación de anisotropía de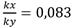 
. Las propiedades físico-mecánicas empleadas en la modelación se muestran en la tabla 1 y las curvas granulométricas de los suelos se muestran en la figura 3.
Tabla 1 Propiedades físico-mecánicas de los suelos del terraplén.
| No. Suelo | mv (kPa-1) | CVA (adim.) | LL (%) | kx (m/s) | e (adim.) | γ (kN/m3) | C´ (kPa) | Φ´ (°) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5,61E-05 | 0,421 | 57 | 1,50E-07 | 0,726 | 18,3 | 30,9 | 13,5 |
| 2 | 1,05E-04 | 0,428 | 47 | 1,10E-07 | 0,749 | 18,8 | 56,8 | 13,4 |
| 3 | 5,06E-05 | 0,406 | 38 | 6,60E-08 | 0,683 | 18,9 | 18,6 | 13,2 |
| 4 | 9,34E-05 | 0,391 | 72 | 1,50E-07 | 0,642 | 17,9 | 29,8 | 17,6 |
| 5 | 7,42E-05 | 0,439 | 60 | 8,70E-08 | 0,783 | 19,2 | 42,1 | 15,4 |
| 6 | 6,64E-05 | 0,503 | 39 | 4,70E-07 | 1,013 | 18,8 | 32 | 21,3 |
| 7 | 6,52E-05 | 0,455 | 39 | 1,70E-07 | 0,836 | 19 | 22,1 | 14,3 |
| 8 | 8,88E-05 | 0,496 | 56 | 1,20E-06 | 0,984 | 18 | 43,7 | 13,2 |
| 9 | 1,42E-04 | 0,426 | 56 | 6,00E-07 | 0,741 | 17,3 | 40,6 | 14,9 |
| 10 | 6,36E-05 | 0,425 | 57 | 1,80E-07 | 0,739 | 18,5 | 57,5 | 27,1 |
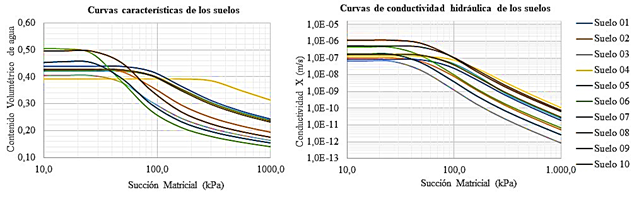
En la figura 4 se muestran las curvas características empleando el modelo de Aubertin et al. (2003) y las curvas de conductividad hidráulicas correspondientes, mediante el método de Fredlund et al. (1994).
Para la determinación de las intensidades de lluvia a emplear, se tomó como referente el estudio realizado por Barcia y León (2013), donde se exponen las curvas de intensidad-frecuencia-duración (IFD) de la lluvia para la localidad de Cienfuegos, determinadas a partir de datos pluviométricos medidos en el período 2001-2010, para una duración máxima de 24 horas, a partir de las cuales se seleccionaron las intensidades correspondientes a 5, 10, 25 y 50 años de período de retorno. Estas intensidades de lluvia fueron afectadas por el coeficiente de infiltración propuesto por Schosinsky (2007), que para las condiciones de los taludes aguas abajo de las presas de tierra en Cuba se estimó en 27%. En la tabla 2 se muestra la velocidad de infiltración de la lluvia correspondiente a la intensidad y los períodos de retorno establecidos.
Resultados de la modelación
Una vez definidas las variantes que intervienen en el proceso de modelación, se construyó un modelo numérico con el programa GeoStudio (2018). Inicialmente, se realizó la modelación del flujo de filtración estacionario, sin lluvia, para establecer la posición de la línea de corriente superior y la superficie drenante en el talud aguas abajo. Luego, se impuso la condición de infiltración de la lluvia sobre la superficie del talud aguas abajo, exceptuando la sección del mismo en la que ocurre el drenaje del flujo de filtración. Todo ello se muestra en la figura 5.
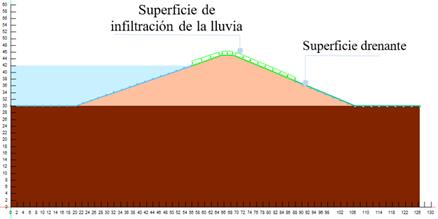
Figura 5 Modelo numérico resultante con la aplicación de la superficie de infiltración de la lluvia y la superficie drenante.
Se realiza un análisis del avance del frente de saturación correspondiente al efecto de la lluvia en la LCS de los terraplenes, para los 10 suelos estudiados en las diversas condiciones planteadas. El resultado correspondiente a los períodos de retorno de 5 años (menor) y 50 años (mayor), tomado como ejemplo el suelo 10, se muestran en la figura 6.
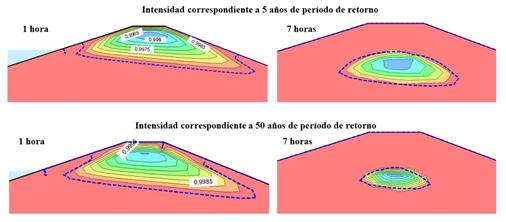
Figura 6 Avance del frente de saturación para el suelo 10, entre las horas 1 y 7 de lluvia para 5 y 50 años de período de retorno.
En la figura 6 se puede observar que el frente de filtración en la primera hora de lluvia se comporta prácticamente igual para ambos períodos de retorno. Sin embargo, una vez transcurridas siete horas, el área saturada (indicada en color naranja en la figura 6) resulta cada vez mayor. Esto ocurre debido a que los mayores períodos de retorno se asocian con las mayores intensidades de lluvia, lo que provoca que al suelo se infiltre una mayor cantidad de agua en un menor período de tiempo independientemente del tipo de suelo.
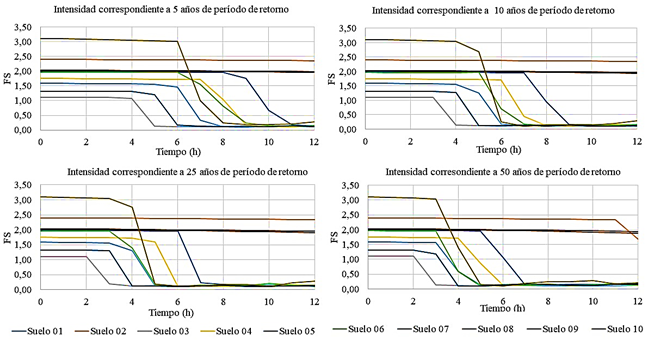
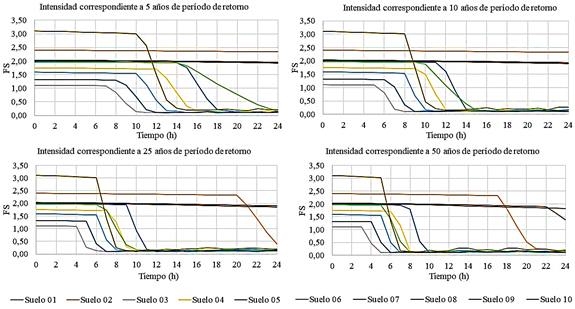
Luego, se analiza el comportamiento del FS en función del tiempo para los 10 suelos definidos y las intensidades de lluvia correspondientes a los 5, 10, 25 y 50 años de período de retorno para 12 y 24 horas. Estos resultados se muestran en las figuras 7 y 8.
Como se puede observar en las figuras 7 y 8, en la medida que los períodos de retorno son mayores, o sea, las intensidades de lluvia aumentan, el tiempo que tarda en desencadenarse la falla disminuye para todos los suelos estudiados. Se aprecia además que, en las menores intensidades de lluvia, que corresponden con los menores períodos de retorno, la falla no ocurre en todos los suelos, como es el caso de los suelos 2, 8 y 9. Sin embargo, a medida que aumenta la intensidad, se producen las fallas de forma gradual en todos los suelos. De manera general, queda demostrado que las menores intensidades de lluvia que se sostienen durante un mayor período de tiempo, son más peligrosas para la estabilidad de taludes en una presa de 15 metros de altura con las características de la estudiada en la presente investigación.
Llegados a este punto, resulta necesario analizar los parámetros del suelo que pueden provocar la divergencia en los tiempos de ocurrencia de las fallas. Para ello, se evalúa la relación entre el índice de poros y permeabilidad para todos los suelos estudiados y las intensidades y tiempos de duración de la lluvia. Los resultados correspondientes a 24 horas de duración de la lluvia se muestran en las figuras 9 y 10.
Figura 9 Relación entre el tiempo de falla y la relación de vacíos para 24 horas de duración de la lluvia.
Figura 10 Relación entre el tiempo de falla y la permeabilidad para 24 horas de duración de la lluvia.
En la figura 9 se observa que, para bajas intensidades de lluvia, la relación de vacíos y el tiempo de falla tienen una relación directamente proporcional. En la medida que la intensidad de la lluvia aumenta, la influencia de la relación de vacíos en el tiempo de ocurrencia de la falla va disminuyendo, hasta convertirse en una relación inversamente proporcional. En cuanto a la permeabilidad, (figura 10), esta sigue el mismo comportamiento respecto al tiempo de falla, que el observado en la relación de vacíos. A mayor intensidad de la lluvia, menos influencia ejerce la relación de vacíos y la permeabilidad en la ocurrencia de la falla.
Los resultados correspondientes a 12 horas de duración de la lluvia mostraron la misma tendencia en el comportamiento. La única distinción respecto a la duración de 24 horas es que, para las intensidades correspondientes a los períodos de retorno menores, la relación directamente proporcional que se establece es mucho menos manifiesta. Este comportamiento se ajusta con los resultados previos que se presentaron en la presente investigación, que relacionan una mayor rapidez en la ocurrencia de la falla para mayores intensidades de lluvia durante menores períodos de tiempo.
Conclusiones
En todos los modelos analizados se pudo observar que, para las lluvias de menor intensidad, pero larga duración (24 horas) los parámetros del suelo como índice de poros y permeabilidad son determinantes en la ocurrencia de la falla para los casos de las lluvias con menor período de retorno (5 y 10 años). Mientras que, para períodos de retornos mayores (25 y 50 años) los parámetros: índice de poros y permeabilidad se comportan de forma inversamente proporcional al tiempo de ocurrencia de la falla. Para las lluvias de menor tiempo de duración (12 horas) y mayores intensidades, se mantiene el mismo comportamiento, pero de manera mucho menos manifiesta que para la duración de 24 horas.
Se observa que, aunque los valores de los parámetros de resistencia a cortante son determinantes para el FS inicial del talud, estos no influyen en la forma ni el tiempo en el que ocurre la falla bajo el efecto de la lluvia, demostrando que la permeabilidad, el índice de poros del suelo y la intensidad de la lluvia son los que priman en el momento de ocurrencia de la falla, independientemente de los restantes parámetros físico-mecánicos del suelo.
