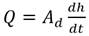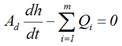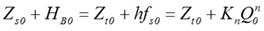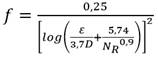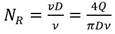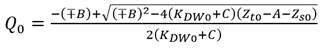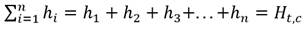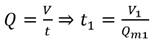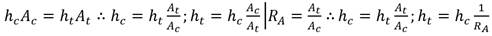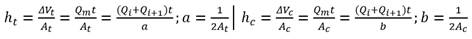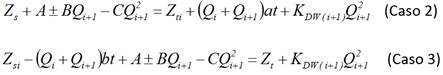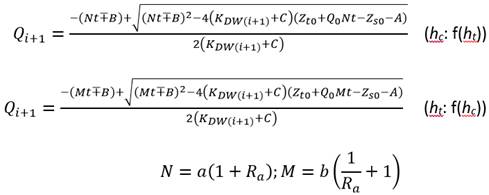Artículo de investigación

Determinación del tiempo de llenado y/o vaciado de depósitos en sistemas fuentes por bombeo

Determination of the filling and / or emptying time of tanks in pumped source systems

0000-0001-9770-022XYaset Martínez Valdés^{1  *}  , 0000-0003-4198-9962David Ernesto Marón Domínguez¹ 

¹ Centro de Investigaciones Hidráulicas (CIH), Facultad de Ingeniería Civil, Universidad Tecnológica de La Habana “José Antonio Echeverría”, Cujae.

RESUMEN

En el presente trabajo se propone una metodología de cálculo para determinar los tiempos de llenado y/o vaciado de los depósitos en los sistemas fuente por bombeo. La misma, se centra en la resolución de un modelo de cálculo discreto que tiene en cuenta las principales variables hidráulicas que caracterizan tres esquemas o casos de diseño y operación en dichos sistemas. Se presentan dos modelos de cálculo de enfoque discreto en función de la altura y el tiempo, los cuales se implementan en el sistema de cómputo numérico matlab versión r2013b para la comparación de diferentes variantes de los esquemas de diseño descritos. Ambos procedimientos analíticos se emplean en la resolución de un ejemplo práctico donde se ilustran los tres casos de operación para distintas variantes y alternativas de cálculo.

Palabras-clave: tiempo; llenado; vaciado; depósitos; bombeo

ABSTRACT

In the present work, a calculation methodology is proposed to determine the filling and / or emptying times of the tanks in the pumping source systems. It focuses on solving a discrete calculation model that takes into account the main hydraulic variables that characterize three schemes or cases of design and operation in these systems. Two discrete approach calculation models are presented as a function of height and time, which are implemented in the MATLAB version R2013b numerical computing system for the comparison of different variants of the design schemes described. Both analytical procedures are used to solve a practical example where the three cases of operation are illustrated for different variants and calculation alternatives.

Key words: time; filling; emptying; tanks; pumping

Introducción

Un sistema de abastecimiento de agua es un sistema dinámico cuyas variables cambian constantemente: consumos, nivel de los depósitos, estaciones de bombeo que arrancan y paran, etc. Cuando la variación de los principales parámetros (presión, caudal, niveles en los depósitos, etc.) sea pequeña o se produzca muy lentamente, un análisis en régimen permanente resulta adecuado. Esta representación temporal es una analogía de “n” instantáneas del sistema. La escala de tiempo en la que se producen estas variaciones es imprescindible para escoger el tipo de modelo de estudio: régimen variable o transitorio (^{Cabrera 1996}).

En el caso del estudio de la evolución de los niveles en un depósito u optimizar el régimen de bombeo a lo largo de un periodo de tiempo, será necesario utilizar modelos de simulación dinámica. Este tipo de modelo es válido solo cuando las variaciones de las variables hidráulicas en el tiempo no son bruscas. Este modelo se basa en el análisis de sucesivos estados estacionarios correspondientes a intervalos de tiempo determinados. En la transición de un intervalo a otro, varían los consumos, el estado de los elementos de regulación, el nivel de los depósitos, etc., aunque durante el intervalo se suponen constantes. Siempre que se garanticen el cumplimiento de estas condiciones, los modelos de simulación dinámica proporcionan la representación más precisa y sencilla del funcionamiento de los sistemas de distribución, pues formalmente se plasma un sistema de ecuaciones algebraicas que caracterizan el sistema (^{Hernández, Gómez y Zanzi 2016}a).

El objetivo del análisis en régimen permanente de un sistema de distribución de agua consiste en obtener los caudales circulantes por las conducciones, la carga a presión y los niveles en los depósitos, mediante la resolución de un sistema de ecuaciones de equilibrio (ecuación de conservación de la masa, o de Continuidad y ecuación de conservación de la energía) que caracteriza al sistema de abastecimiento a partir de conocer la carga piezométrica o carga de presión de un nudo al menos, las características hidráulicas de las conducciones (diámetros, rugosidades y longitud) y las características relevantes del resto de los elementos del sistema (válvulas, accesorios, bombas, etc.) (^{Hernández, Gómez y Zanzi 2016}b).

Los sistemas fuentes por bombeo están constituidos por: fuente(s) de agua, estaciones de bombeo, sistemas de tuberías de conducción, sistema de protección contra el golpe de ariete, depósitos de regulación y/o compensación, entre otros objetos de obra secundarios. Los modelos de simulación en régimen cuasi-permanentes permiten una mejor comprensión del comportamiento hidráulico de los sistemas fuentes por bombeo y sus respuestas a los diferentes condicionantes que se les van imponiendo a lo largo del tiempo, constituyendo un instrumento eficaz en su gestión.

En el presente trabajo se propone una metodología de cálculo para determinar los tiempos de llenado y/o vaciado de los depósitos en los sistemas fuente por bombeo. La misma, se centra en la resolución de un modelo de cálculo discreto que tiene en cuenta las principales variables hidráulicas que caracterizan tres esquemas de operación en los sistemas fuente por bombeo. Estos pueden ser descritos a partir de un esquema típico de diseño común: depósito de succión (sección regular uniforme) → tubería(s) de succión (válvulas, accesorios, etc. se incluyen mediante su longitud equivalente característica) → bomba(s) → tubería de impulsión (válvulas, accesorios, etc. se incluyen mediante su longitud equivalente característica) → depósito de descarga (sección regular uniforme).

El modelo de cálculo de enfoque discreto se implementa en el sistema de cómputo numérico MATLAB versión R2013b para la comparación de diferentes variantes de los esquemas descritos. El procedimiento analítico se emplea en los tres casos de operación a partir de distintas variantes y alternativas de cálculo que reflejan datos reales de las instalaciones de los esquemas descritos. Debido a que este tema no ha sido abordado con profundidad en la literatura, y debido al gran interés que presenta en el análisis y simulación de los sistemas fuente por bombeo, es que se ha decidido abordar esta temática en el presente trabajo.

Desarrollo

Los sistemas fuente por bombeo se pueden clasificar en simples y complejos a partir de su conformación topológica, desde la fuente de agua hasta el nodo o punto de entrega. Los diferentes esquemas de diseño y operación de los sistemas fuentes por bombeo estarán en función de las características de la toma de succión y descarga y si la demanda es continua (gasto constante) o variable en el tiempo (gasto variable) independiente del tiempo de servicio (^{Martínez, 2011}).

Como se apuntó anteriormente, en esta investigación se trabajará con el esquema de diseño y operación de los sistemas fuentes por bombeo de mayor presencia en la práctica (esquematizado según la dirección del flujo): Fuente de abasto (depósito de succión de sección regular uniforme) → tubería(s) de succión (válvulas, accesorios, etc. se incluyen mediante su longitud equivalente característica) → estación de bombeo (bomba(s) de iguales características hidráulicas) → conductora o tubería de impulsión (válvulas, accesorios, etc. se incluyen mediante su longitud equivalente característica) → depósito de regulación o compensación (entrada libre y forzada con cota de entrega fija) (^{Martínez 2011}).

El modelo cuasi-estático, ampliamente utilizado para la simulación en periodo extendido, viene caracterizado por las ecuaciones algebraicas definidas por las ecuaciones de conservación de energía (Ecuación de Bernoulli) y la de pérdidas de carga (Darcy-Weisbach), y al menos una condición de contorno que varíe lentamente en el tiempo (contorno dinámico del depósito).

Los depósitos ya sirvan de fuente de abasto (depósitos de succión: tanques o cisternas) o de descarga o almacenamiento (tanques de regulación o de compensación), es un clásico ejemplo de contorno dinámico que varía lentamente con el tiempo, a poco que su capacidad tenga una cierta entidad en relación con los caudales salientes y entrantes. En consecuencia, un sistema hidráulico con depósitos constituye una aplicación clara y típica de una simulación cuasi-estática. Cómo es conocido, la variación del nivel en un depósito viene dada por la ecuación diferencial ordinaria (^{Fuertes et al. 2007}):

(1)

Dónde:

Q	caudal entrante o saliente al/del depósito, (m^3/s)
Ad	sección en planta del depósito, (m^2)
h	nivel del agua en el depósito, (m)
t	tiempo de llenado o vaciado del depósito, (s)

En el supuesto de que el depósito se vaciase, el término de la derecha de la ecuación sería negativo y el caudal del miembro izquierdo de la misma pasaría a ser Qs o caudal saliente. Cuando sucede el caso contrario (llenado del depósito), ambos miembros de la ecuación son positivos y el gasto pasaría a denominarse caudal entrante, Qe.

Descripción de los casos de estudio para la determinación de los tiempos de llenado y/o vaciado de los depósitos en los sistemas fuente por bombeo

A partir del esquema típico de diseño definido, se describen los cuatro casos de estudio de mayor presencia en la práctica ingenieril, los cuales mantienen la misma tipología de diseño, variándose solamente las condiciones hidráulicas y de operación de dichas instalaciones. Para los objetivos que se pretenden exponer en este trabajo, el desarrollo de la metodología de cálculo se realiza solamente para los casos 2, 3 y 4, ya que el caso 1, al mantenerse constante el gasto de bombeo en el tiempo, este puede obtenerse mediante la ecuación de aforo volumétrico. Los cuatro casos de estudio son los siguientes:

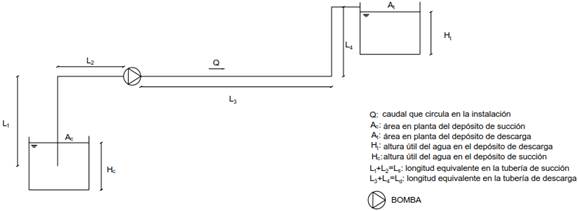
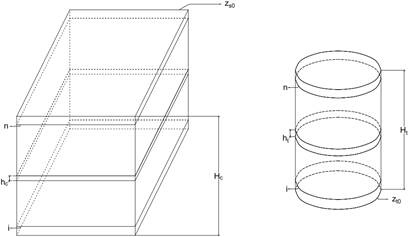
Caso 1: La entrada de agua al depósito de descarga es por la parte superior de este (entrega libre con cota fija), donde se succiona de un depósito en el cual se considera que el nivel de agua se considera fija (nivel en la succión no varía en el tiempo) (véase figura 1). En términos de operación, este es el único caso en el cual se mantiene constante el gasto de bombeo a lo largo del tiempo.

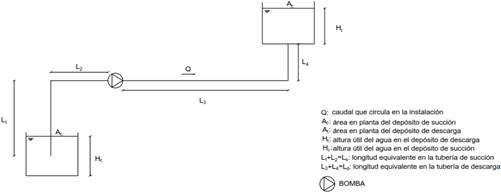
Caso 2: La entrada de agua al depósito de descarga es por la parte inferior de este (entrega forzada con cota fija) y el nivel del agua en el depósito de succión no varía en el tiempo. Este esquema de operación afecta en el gasto que entrega la bomba durante todo el intervalo de llenado del depósito de descarga (véase figura 2). Para este caso, el objetivo es calcular el tiempo de llenado del depósito de descarga, t _ll .

Figura 1 Esquema de diseño y operación de los Casos 1 y 3. 

Caso 3: La entrada de agua al depósito de descarga es por la parte superior (entrega libre con cota fija) a la vez que disminuye el nivel en el depósito de succión producto del bombeo. Este esquema de operación afecta en el gasto que entrega la bomba durante todo el intervalo de vaciado del depósito de succión (véase figura 1). Para este caso, el objetivo es calcular el tiempo de vaciado del depósito de succión, t _v .

Caso 4: La entrada de agua al depósito de descarga es por la parte inferior (entrega forzada con cota fija) a la vez que varía el nivel en el depósito de succión. Este esquema de operación implica que, a medida que se llena el depósito de descarga se vacía el de succión, lo cual repercute en el gasto que entrega la bomba, el cual se reduce en el tiempo, en este caso, por el “doble efecto” de la entrada forzada al depósito de descarga y la disminución gradual en el tiempo del nivel del agua en el depósito de succión (véase figura 2). Para este caso es evidente que el tiempo de llenado y vaciado de ambos depósitos es el mismo, por lo cual basta con solo calcular uno de ellos, t _ll o t _v .

Figura 2 Esquema de diseño y operación de los Casos 2 y 4. 

Procedimiento de cálculo para la determinación de los tiempos de llenado y/o vaciado de los depósitos en los sistemas fuente por bombeo

Como se ha comentado anteriormente, un aspecto fundamental en la simulación de sistemas fuente por bombeo en régimen cuasi-permanente, es la forma en que se efectúa la integración del balance de caudales en cada depósito, con la finalidad de calcular las fluctuaciones de los respectivos niveles de agua a lo largo del tiempo. La dinámica en los depósitos se rige por ecuaciones diferenciales ordinarias, resultantes de la aplicación de la ecuación de Continuidad a cada depósito en el sistema fuente por bombeo. En su formato más general, la caracterización del contorno depósito responde a la ecuación característica (^{Pulido, Gutiérrez and Asensio 2006}):

(2)

Dónde:

Ad	sección en planta del depósito, (m^2)
h	nivel del agua en el depósito, (m)
t	tiempo de llenado o vaciado del depósito, (s)
Q	caudal afluente o efluente al depósito, (m^3/s)
m	número de tuberías que convergen al depósito, (adim.)

Existen varias técnicas numéricas que permiten la resolución de la ecuación diferencial (2). La elección del método a emplear dependerá del tipo de problema a resolver. De hecho, las técnicas más simples están sustancialmente afectadas por el intervalo de discretización Δt utilizado (intervalo de tiempo entre dos estados de régimen permanente consecutivos), recomendándose la utilización de pequeños valores de este. Las técnicas más sofisticadas permiten, en general, obtener resultados numéricos más precisos para un mismo intervalo de discretización, con el inconveniente de la exigencia de un mayor tiempo de cálculo para cada intervalo de discretización (^{Cabrera 1996}).

Las dos técnicas de cálculo alternativas más utilizadas son la técnica explícita y el método de previsión-corrección (técnica implícita). La primera se basa en la aplicación del método de Euler para calcular la cota de la superficie libre en el depósito en el instante (t + Δt), a partir de conocer dicha cota en un instante previo t. Por su parte, el método de previsión-corrección es una técnica implícita más precisa para integrar la ecuación 2. Fue elaborado por ^{Rao y Bree (1977}) basándose en el método de Euler modificado y utilizando un esquema de previsión-corrección. Se clasifica como un método implícito, ya que en su formulación no se conoce a priori el caudal en el instante posterior Q (t + Δt). De hecho, este caudal es función de las cotas de los niveles de agua en los depósitos del sistema en el instante (t + Δt), las cuales son también previamente desconocidas (^{Cabrera 1996}).

Como puede notarse, ambas técnicas de cálculo basan sus algoritmos de solución en función de la variable tiempo. La metodología que se propone, establece un procedimiento analítico para la determinación del tiempo de llenado y/o vaciado de los depósitos en los sistemas de bombeo, bajo el principio de que los depósitos solo se llenan y/o vacían mediante la acción del bombeo. Para los casos de estudio señalados esto significa que: para el caso 2, el depósito de descarga se llena sin presencia de un caudal efluente de este; para el caso 3, el depósito de succión se vacía solamente debido a que no hay un caudal afluente a este; mientras que para el caso 4, se produce el vaciado y llenado a la vez de los depósitos de succión y descarga, respectivamente, sin existir caudales de entrada o salida hacia o desde dichos depósitos.

El procedimiento analítico para la simulación temporal de estos tres esquemas de diseño, se basa en dos métodos de resolución basados en un enfoque discreto en función de la discretización de la altura, Δh y del tiempo, Δt. La base conceptual detrás de estos dos métodos reside en el trabajo conjunto de la ecuación de conservación de energía (Ecuación de Bernoulli) y la ecuación de aforo volumétrico para el cálculo de los diferentes Δh o Δt en función del método empleado. Ambas vías de cálculo cumplen el mismo objetivo, comprometiendo el uso de una variante u otra a los resultados que se deseen obtener. Por ejemplo, si se pretende conocer el tiempo de bombeo que se requiere para llenar o vaciar un depósito una altura determinada, se debe usar el método de discretización en función de la altura. Por otro lado, con el método de discretización del tiempo, se puede calcular para un lapso dado, la altura de vaciado o llenado de un depósito. A continuación, se presentan las dos técnicas de cálculo alternativas en su modelo desarrollado y, posteriormente, se efectuará una comparación entre los resultados obtenidos.

Modelo discreto en función de la altura

El proceso de simulación consiste de los siguientes pasos:

1. Para el instante t ₀ (instante inicial de la simulación) son conocidos los siguientes datos: información reológica (deben garantizarse que no cambian en el tiempo), características hidráulicas de las bombas (polinomios representativos de las curvas características) y del sistema de tuberías (materiales, diámetros, presión nominal de diseño y rugosidades absolutas), niveles de agua en los depósitos de succión y descarga, consumos en los nudos de unión (si existiere), números de tuberías que convergen o salen de los depósitos y la ecuación del área en planta del tanque en función de la altura del tanque (si los depósitos tienen tipología prismáticas o circulares, esta expresión es una constante igual al área en planta de los depósitos)

2. Para t ₀ se determinan las condiciones de equilibrio hidráulico utilizando las ecuaciones básicas referidas en régimen permanente, lo que permite el cálculo del caudal, Q ₀ en el sistema y las cargas a presión en los nudos (si existieren). Para los depósitos, la solución anterior permite obtener los caudales de entrada y/o salida (llenado y/o vaciado). Para el instante inicial, t ₀ la secuencia de cálculo sería:

A partir de la ecuación de Bernoulli aplicada para el instante inicial se obtiene (3):

(3)

Dónde:

Z s0	cota topográfica del nivel del agua en el depósito de succión para t 0 , (m)
H B0	carga que desarrolla la bomba para el caudal entregado en el instante inicial, Q o , (m)
Z t0	cota topográfica del nivel del agua en el depósito de descarga para t 0 , (m)
hf s0	pérdidas de carga que se producen en el sistema de tuberías para Q o , (m)
K n	coeficiente característico de la conducción, (s^2/m^5).

Introduciendo en la expresión 3 el polinomio representativo de la curva característica H _B vs. Q, y calculándose las pérdidas de carga a partir de la ecuación de Darcy-Weisbach, se obtiene la expresión 4:

(4)

(5)

Dónde:

hf DW	pérdidas de carga en la conducción obtenidas por la fórmula de Darcy-Weisbach (m)
hf DW0	pérdidas de carga en la conducción obtenidas por la fórmula de Darcy-Weisbach para el instante t 0 (m)
f	coeficiente de fricción de la tubería determinado por la fórmula de Swamee-Jain, (adim.)
L eq	longitud equivalente del sistema, (m)
D	diámetro interior de la tubería, (m)
Q	caudal de circulación, (m^3/s)
K DW	coeficiente característico de la conducción, (s^2/m^5)
K DW0	coeficiente característico de la conducción para el instante t 0 , (s^2/m^5)
A	coeficiente del polinomio representativo de la curva H vs. Q que define el valor de la carga que desarrolla la bomba para caudal cero, (m)
B	coeficiente del polinomio característico de la curva H vs. Q que depende de la geometría del diseño de la bomba, (s/m^2)
C	coeficiente del polinomio específico de la curva H vs. Q que está en función de las pérdidas de carga en el interior de la bomba, (s^2/m^5).

(6)

Dónde:

f	coeficiente de fricción de la tubería, (adim.)
ε	rugosidad absoluta asociada al material de la tubería
(m); D	diámetro interior de la tubería
(m) y N R	número de Reynolds que caracteriza el flujo en la conducción, (adim.)

(7)

Dónde:

N R	número de Reynolds que caracteriza el flujo en la conducción
(adim.); v	velocidad media de circulación en la tubería
(m/s); D	diámetro interior de la tubería
(m); (	viscosidad cinemática del fluido
(m^2/s) y Q	caudal de circulación en la conducción, (m^3/s)

Introduciendo la expresión 5 en la 4, y resolviendo la ecuación de segundo orden resultante por el Teorema de Cardano-Vieta, se obtiene la siguiente expresión para el caso del instante inicial: expresión 8

(8)

El valor de K _DW0 correspondiente para t ₀ depende del valor de f ₀ , lo cual deriva en un proceso iterativo en función de f:

2.1. Suponer un valor de f ₀

2.2. Calcular K _DW0 a través de la expresión 5

2.3. Calcular Q ₀ por la ecuación 8

2.4. Calcular el valor de f ₀ a partir de Q ₀ obtenido en el paso anterior

2.5. Comparar el valor de f _0c con el valor supuesto en el primer paso, teniendo en cuenta un error relativo de parada, ξ_r ( 1%. Si esta condición no se cumple debe repetirse la rutina de cálculo hasta garantizar su consecución

3. Una vez obtenido el valor de Q ₀ se procede con un proceso de discretización en función de Δh. Los valores de Δh pueden asumirse constantes o variables a lo largo de la altura del depósito, siendo la primera opción la más adecuada para depósitos de sección regular prismática. Como se ha apuntado anteriormente, mientras más pequeños sean los valores de Δh, se podrán obtener resultados numéricos más precisos. En este paso se procede a asumir el primer valor de h, h ₁ siendo válido recordar que: H _t y/o H _c (según sea el caso) queda definido como la sumatoria de los diferentes intervalos h (h ₀ = 0 (depósito de descarga vacío o depósito de succión lleno) para el instante inicial t ₀ = 0), sean iguales o diferentes, según la siguiente expresión 9:

(9)

1. Con el valor de h ₁ se procede a calcular el volumen correspondiente a esa primera dovela atendiendo a la figura 3, como: V ₁ = A·h ₁. Es evidente que la sumatoria de los diferentes volúmenes será el volumen del depósito. El valor de h ₁ se utilizará también para calcular la nueva cota Z _t1 correspondiente a la cota topográfica del nivel del agua en el depósito de descarga para el tiempo t ₁ como: Z _t1 = Z _t0 + h ₁

2. Con estas dos variables definidas (V ₁ y Z _t1 ), se pasará a repetir el paso 2 ahora para el cálculo de Q ₁ , donde quedarán definidos en el proceso f ₁ y K _DW1

3. Con ambos valores de gastos, Q ₀ y Q ₁ se procede a determinar el caudal medio, Q _m1 que entra o sale de los depósitos en el intervalo de t ₀ a t ₁ , correspondiente a esa primera dovela

Figura 3 Esquemas de dos tipologías típicas de depósitos de sección regular. 

4. Por último, con Q _m1 y el V ₁ se calcula el t ₁ mediante la ecuación de aforo volumétrico:

(10)

Dónde:

Q	caudal de llenado o vaciado de un depósito mediante bombeo
(m^3/s); V	capacidad volumétrica de un depósito
(m^3) y t	tiempo de llenado del depósito, (s).

5. Repetir el procedimiento para nuevos valores de h en el depósito para determinar los respectivos valores de tiempo de llenado o vaciado de cada dovela diferencial, t según sea el caso. El tiempo de llenado, t _ll o de vaciado, t _v de un depósito total o parcial, se calculará a través de la siguiente sumatoria de los tiempos de llenado o vaciado de cada dovela:

(11)

Para la aplicación del método del modelo discreto en función de la altura hay que tener en cuenta varias particularidades que responden a cada caso. En este sentido los casos 2 y 3 se pueden considerar homólogos desde el punto de vista hidráulico. Atendiendo a esto, la ecuación 8 queda configurada para las n dovelas del depósito, para ambos casos, como:

(12)

Vale la pena recordar que en el caso 2 el nivel del agua en el depósito de succión se mantiene constante, Z _s , mientras que en el caso 3 esto es una condición establecida para el depósito de descarga, Z _t . En ambas ecuaciones, h _t y h _c se toman como las variaciones del nivel del agua definidas para los depósitos de descarga (Caso 2) y succión (Caso 3) respectivamente.

Tratamiento aparte amerita el Caso 4, el cual se puede tomar como el caso general de este tipo de problemas. Como se ha descrito arriba, y atendiendo a la particularidad del mismo, se deduce que existe una relación entre los volúmenes de los depósitos de aspiración, V _c y descarga, V _t , tal que: V _c = V _t , a partir de considerar que no existen aportes ni salidas de volúmenes al sistema. Observando ese principio, se derivan las siguientes formulaciones:

(13)

Dónde:

h c	variación de nivel en el depósito de succión
(m); A c	área de la sección en planta del depósito de succión
(m^2); h t	variación de nivel en el depósito de descarga
(m); A t	área de la sección en planta del depósito de descarga
(m^2) y R A	relación de áreas de los depósitos, (adim.)

Introduciendo en la ecuación 12 las relaciones descritas en la expresión 13 se obtienen las siguientes expresiones expresión 14:

(14)

Modelo discreto en función del tiempo

El procedimiento analítico está estructurado por los siguientes pasos, de los cuales, los dos primeros, son los mismos para ambos métodos de cálculo, por lo cual se comienza desde el 3er paso:

3. Una vez obtenido el valor de Q ₀ se procede con un proceso de discretización en función de Δt. Es recomendable asumir valores constantes de Δt, sobre todo si se trata de depósitos de sección regular prismática. Al igual que en el caso del modelo de solución anterior, mientras más pequeños sean los valores de Δt (discretización más fina), se podrán obtener resultados numéricos más precisos. En este paso se adopta el concepto definido a través de la ecuación 11, asumiendo que, para el instante inicial, t ₀ = 0.

4. A partir de introducir las siguientes relaciones (ecuación 15) en la expresión 4 para el cálculo del caudal en el instante t _i+1 , se obtiene la ecuación 16 para los Casos 2 y 3:

(15)

(16)

Tomando como referencia esta última ecuación, las soluciones para ambos casos para un tiempo t se determinan como: expresión 17:

(17)

Como parte del proceso de cómputo de los caudales Q _i+1 , se calcularán los respectivos coeficientes de fricción, f _i+1 y K _DW(i+1) según lo apuntado en el paso 2.

3. Una vez que se calcule un gasto, se trabajará con las relaciones definidas en la ecuación 15 en función del caso que se trate para determinar h _t o h _c para cada intervalo de tiempo, t

4. Se repetirá este proceso hasta lograr completar la altura útil del depósito que se evalúa según el caso (llenado: Caso 2 y vaciado: Caso 3) atendiendo al concepto de la ecuación 9.

A partir del significado que enuncia la expresión 13 y las relaciones a y b de la ecuación 15, se adapta la expresión 17 en función de la variable de referencia de medición, h _c o h _t , obteniéndose para el Caso 4: expresión 18

(18)

Se presenta a continuación un ejemplo de aplicación de la metodología propuesta para ambos modelos discretos, con el objeto de exponer sus posibilidades, capacidades de solución y limitaciones operativas. Se ha procurado mostrar a un ejemplo práctico sencillo, aunque suficientemente ilustrativo para garantizar una mejor comprensión del procedimiento analítico de ambas soluciones. Para la resolución del mismo se ha empleado el software MATLAB versión R2013b para las tres variantes de esquemas de operación (Casos 2, 3 y 4).

Cálculo del tiempo de llenado y/o vaciado de un depósito en un sistema fuente por bombeo

La información del sistema fuente por bombeo para los tres casos que se analizarán es la siguiente: diámetro exterior de la conductora, D = 450 mm; diámetro interior de la conductora, D _c = 396,6 mm; material de la tubería: polietileno de alta densidad (PEAD); rugosidad absoluta media del material, ε = 2,5·10^-3 mm; presión nominal de diseño, PN = 10 atm.; longitud de la tubería, L _c = 1000,00 m; cota topográfica del nivel del agua en el depósito de succión para t ₀ , Z _s0 = 15,00 m (Casos 3 y 4) y Z _s = 15,00 m (Caso 2); cota topográfica del nivel del agua en el depósito de descarga para t ₀ , Z _t0 = 58,00 m (Casos 2 y 4) y Z _t = 63,00 m (Caso 3); área de la sección en planta del depósito de succión, A _c = 1054,00 m²; área de la sección en planta del depósito de descarga; altura útil del depósito de descarga, H _t = 5,00 m (Casos 2 y Caso 4); altura útil del depósito de aspiración, H _c = 3,00 m (Caso 3); A _t = 527,00 m² y coeficientes del polinomio representativo de la curva H vs. Q de la bomba: A = 80,092 m, B = 11,384 s/m² y C = -571,588 s²/m⁵.

Para el proceso de cálculo de los coeficientes de fricción, f se utilizó un criterio de parada en base a un error relativo de 10^-6, aplicable por transitividad al cálculo de los caudales para cada intervalo de tiempo, Q _i . Se tomó como criterio para la discretización los siguientes valores: Δh = 5 mm (Casos 2 y Caso 4), Δh = 3 mm (Caso 3) y Δt = 10 s (para todos los casos). Basado en esta información, se procede a realizar los cálculos del tiempo de llenado del depósito de descarga (Caso 2), tiempo de vaciado del depósito de succión (Caso 3) y tiempo de llenado y vaciado de ambos depósitos (Caso 4), mediante los algoritmos de solución descritos para ambos modelos, implementados en el software MATLAB versión R2013b.

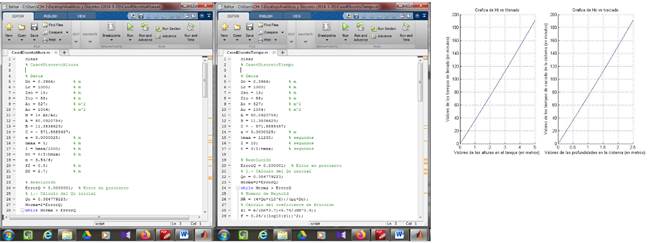
Para el Caso 2 se obtuvieron los siguientes resultados para los dos modelos de solución: Q ₀ = 0,24307 m³/s = 243,07 L/s. Como es de esperar, a medida que se fue llenando el depósito de descarga, el tiempo de llenado por dovela (Δh = h _t = 0,005 m = 5 mm) fue disminuyendo de 0,18068 min. = 10,84 s a 0,19389 min. = 11,63 s. Finalmente, el gasto final correspondiente a la altura útil del tanque (H _t = 5,00 m) fue de Q = 0,22649 m³/s = 226,49 L/s, menor al inicial, como se puede deducir. Para la variante del modelo discreto en función del tiempo, para un intervalo de Δt = 10 s, la altura del depósito que se llena varía de 4,61 mm a 4,95 mm. Para este último tramo, el depósito llega a la altura de 5,0029 m, casi tres milímetros por encima del nivel de agua establecido, situación que hubiera sido bien diferente si el intervalo de discretización fuera mayor. Este resultado ilustra las ventajas apuntadas arriba entre los dos métodos de solución. El tiempo de llenado del depósito de descarga fue de 187,05 min. Los dos procedimientos de cálculo para ambos modelos y su resultado gráfico (H _t vs. t _ll ) se muestran en la figura 4.

Para el Caso 3 se alcanzaron los siguientes resultados para ambos modelos de solución: Q ₀ = 0,22649 m³/s = 226,49 L/s. Para este caso, el tiempo de llenado por dovela (Δh = h _c = 0,003 m = 3 mm) fue disminuyendo de 0,23268 min. = 13,96 s a 0,24406 min. = 14,64 s. Cuando se alcanza la altura útil del tanque (H _c = 3,00 m), el gasto para ese instante es Q = 0,21593 m³/s = 215,93 L/s, menor al inicial como era de esperar. Para el modelo discreto en función del tiempo, para un intervalo de Δt = 10 s, la altura del depósito que se vacía varía de 2,15 mm a 2,25 mm. Para este último intervalo, el depósito se vacía hasta una altura de 3,0012 m, 1,2 mm por encima del nivel de agua establecido. Este resultado muestra nuevamente las ventajas descritas entre los dos métodos de solución y la precisión de estas en función del objetivo que se persiga. El tiempo de vaciado del depósito de succión fue de 238,23 min. Los dos procedimientos de cálculo para ambos modelos y su resultado gráfico (H _c vs. t _v ) se muestran en la figura 5.

Para el Caso 4, el gasto inicial para el instante t ₀ arrojó Q ₀ = 0,24307 m³/s = 243,07 L/s. Se resolvió el procedimiento en función de h _t (Δh = h _t = 0,005 m = 5 mm), obteniéndose una variación del tiempo de llenado de las dovelas de 0,18069 min. = 10,84 s a 0,20169 min. = 12,10 s. En el instante cuando se llena el depósito de descarga (H _t = 5,00 m) el gasto de circulación fue Q = 0,21773 m³/s = 217,73 L/s, menor al inicial, como se puede deducir. Para la variante del modelo discreto en función del tiempo, para un intervalo de Δt = 10 s, la altura del depósito que se llena varía de 4,61 mm a 5,15 mm. Para este último tramo, el nivel del agua en el depósito sobrepasa el permitido en 2,8 mm. El tiempo de llenado y vaciado de los depósitos de descarga y succión, respectivamente, fue de 190,61 min. Los dos procedimientos de cálculo para ambos modelos y sus resultados gráficos (H _t vs. t _ll y H _c vs. t _v ) se muestran en la figura 6.

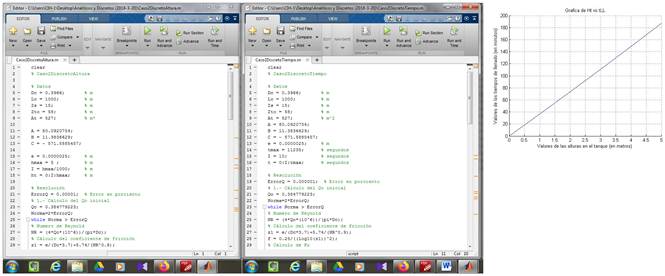
Figura 4 Código de programación del software MATLAB versión R2013b para ambos modelos de solución (altura y tiempo) y gráfica de Ht vs. tll para el Caso 2. 

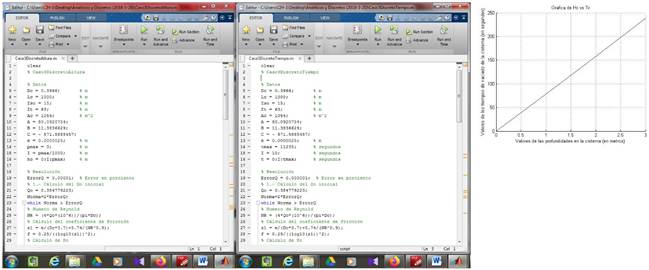
Figura 5 Código de programación del software MATLAB versión R2013b para ambos modelos de solución (altura y tiempo) y gráfica de Hc vs. tv para el Caso 3. 

Figura 6 Código de programación del software MATLAB versión R2013b para ambos modelos de solución (altura y tiempo) y gráficas de Ht vs. tll y Hc vs. tv para el Caso 4. 

Conclusiones

El tema tratado en el trabajo no cuenta con mucha divulgación en la literatura, por lo cual se considera conveniente abordarlo desde la óptica de dos modelos discretos de solución que arrojan el mismo resultado práctico, dependiendo de la respuesta que se persiga. El objetivo del trabajo se centró en la elaboración de dos algoritmos para el cálculo de los tiempos de llenado y/o vaciado de los depósitos en los sistemas fuente por bombeo, basados en dos modelos discretos en función de las variables altura y tiempo, los cuales son implementados mediante la herramienta MATLAB versión R2013b.

Las metodologías de cálculo se aplican a un ejemplo práctico para exponer las diferentes posibilidades de cada modelo de solución para los tres casos de estudio (2, 3 y 4). Se obtienen los tiempos de llenado y/o vaciado de los depósitos para el mismo esquema de operación a partir de los algoritmos implementados en la herramienta MATLAB. Estos procedimientos analíticos serán de gran utilidad en problemas ingenieriles específicos de operación, donde sea necesario tener un estimado del tiempo de llenado y/o vaciado de depósitos en un sistema. En un próximo trabajo se expondrá un método analítico con igual fin y se brindará una comparación con los modelos discretos descritos en el trabajo.

Referencias

1.  Cabrera, E. (1996). “Ingeniería Hidráulica Aplicada a los Sistemas de Distribución de Agua”, 2da Edición, Editorial Unidad Docente Mecánica de Fluidos, Universidad Politécnica de Valencia, t. 1 y 2, ISBN 978-848-94-8701-7, Valencia, España

2.  Fuertes, V. S; Pérez, R; Martínez, F. J; López, P. A. (2007). “Optimización del sistema formado por la estación de bombeo, la tubería de impulsión y el depósito de regulación”, Pimentel H., Pérez R. e Iglesias P. L.. “Abastecimento de água: o estado da arte e técnicas avançadas”, pp.: 261-274, Editorial Universidade Federal da Paraíba, ISBN 978-85-7745-078-3, Paraíba, Brasil

3.  Hernández, J; Gómez, P; Zanzi, C. (2016a). “Mecánica de los Fluidos. Problemas y soluciones”, Editorial Universidad Nacional de Educación a Distancia (UNED), ISBN 978-84-362-7109-6, Madrid, España

4.  Hernández, J; Gómez, P; Zanzi, C. (2016b). “Máquinas Hidráulicas. Problemas y soluciones”, Editorial Universidad Nacional de Educación a Distancia (UNED), ISBN 978-84-362-7004-4, Madrid, España

5.  Martínez, Y. (2011). “Metodología para el diseño hidráulico de las estaciones de bombeo para acueducto”, Tesis de doctorado, Universidad Tecnológica de La Habana “José Antonio Echeverría”, Cujae, La Habana, Cuba

6.  Pulido, I; Gutiérrez, J. C; Asensio, R. (2006). “Optimal design of pumping stations of inland intensive fishfarms”, Aquacultural Engineering, 35 (2006): 283-291, ISSN 0144-8609, Ámsterdam, Holanda

7.  Rao, H. S; Bree, D. W. (1977). “Extend Period Simulation of water systems. Part A”, Journal of the Hydraulics Division, February 1977, Volume 103, Issue 2, ISSN 0044-796X, Virginia, Estados Unidos

Recibido: 06 de Octubre de 2023; Aprobado: 08 de Diciembre de 2023

^* Autor para la correspondencia: [e-mail]

Los autores no declaran conflictos de intereses.

Yaset Martínez Valdés. Participó en el diseño de la investigación y en la elaboración de las metodologías de cálculo para la determinación del tiempo de llenado y/o vaciado de los depósitos en un sistema fuente por bombeo. Colaboró en el procesamiento de los datos del ejemplo abordado en el artículo, haciendo contribuciones en su análisis e interpretación, así como en la búsqueda de información en la literatura especializada y en la redacción final del trabajo.

David Ernesto Marón Domínguez. Realizó contribuciones en el diseño de la investigación y tuvo a su cargo la creación de los algoritmos de cálculo para el software MATLAB 2013b. Participó en el análisis de los resultados del trabajo y en la revisión y redacción del manuscrito en su versión final. Colaboró en el procesamiento de los datos del ejemplo abordado en el artículo, haciendo contribuciones en su análisis e interpretación, así como en la búsqueda de información en la literatura especializada y en la redacción final del trabajo.