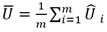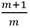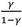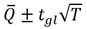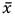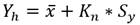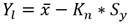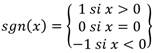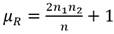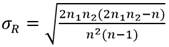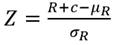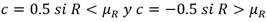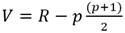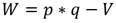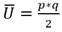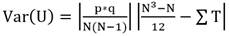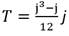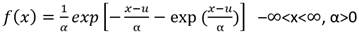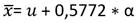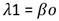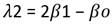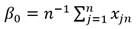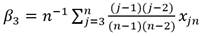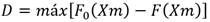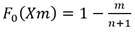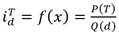Introducción
En los últimos años se ha logrado identificar un cambio en las intensidades de las lluvias, producido por un efecto del cambio climático persistente y agravante. En cuanto a esto, Thiombiano et al., (2017) explican que la temperatura del aire en la superficie en respuesta al forzamiento antropogénico, causa una atmósfera más cálida y húmeda que intensifica el ciclo hidrológico global y resulta en eventos más extremos.
La lluvia se define principalmente por dos variables: magnitud y frecuencia, lo que se conoce como régimen de precipitación. La magnitud de la lluvia se refiere a la precipitación total expresada en milímetros. Por otro lado, la frecuencia está relacionada con la ocurrencia del fenómeno, indicando cuántas veces se presenta. La duración, por su parte, se refiere al período de tiempo durante el cual se mantiene el aguacero, proporcionando información sobre la extensión temporal de la tormenta. La frecuencia en términos de probabilidad se expresa mediante el período de retorno, por lo tanto, se considera que la intensidad de la precipitación es directamente proporcional al período de retorno. Las afectaciones provocadas por este elemento hidrológico son complejas y difíciles de determinar, ya que pueden variar desde inundaciones por grandes avenidas, hasta la inefectividad de sistemas de alcantarillado de drenaje pluvial, por lo que se han tratado de predecir a través de métodos estadísticos.
Con el paso de los años, se han desactualizado los mapas de curvas IDF de la provincia Villa Clara y no se han desarrollado los estudios necesarios para la creación de nuevas curvas. A esto se suma, además la afectación en los últimos tiempos de varios eventos meteorológicos como los huracanes Sandy, Matthew e Irma. También, las obras de diseño del municipio de Caibarién se realizan actualmente con la norma cubana NC 1239:2018 Especificaciones para el diseño y construcción de alcantarillado sanitario y drenaje pluvial urbano, la cual posee unas curvas IDF generales para todo el país y junto al constante cambio climático, se genera un alto grado de incertidumbre a la hora de obtener los datos necesarios para la creación de nuevas obras hidráulicas eficientes y económicas. Teniendo como objetivo la presente investigación, elaborar las Curvas de Intensidad-Duración-Frecuencia asociadas a los eventos lluviosos convectivos en la Estación Meteorológica de Caibarién, en la provincia de Villa Clara.
Metodología para la obtención del esquema tecnológico de la estrategia
La información obtenida de la estación meteorológica de Caibarién se resume y se obtienen los valores máximos de precipitación, dando como resultados las series anuales en rangos horarios de 5, 10, 20, 40, 60, 90, 120, 150, 240, 300, 720, 1440, 2880 y 4320 minutos.
Se realizó un análisis de datos faltantes y datos outliers, utilizándose el método de la imputación múltiple para la ausencia de los datos. Se hace un análisis de la calidad de los datos para comprobar la independencia de la serie, por lo que se utiliza la prueba de Mann-Withney, que tiene la capacidad de comparar las diferencias entre dos medianas, basándose en rangos. Para la detección de tendencias y el análisis de estacionalidad de la serie de datos se formuló la prueba de Mann-Kendall, establecida como una prueba no paramétrica con una distribución estadística, con un amplio uso para detectar tendencias y variación espacial de las series hidroclimáticas.
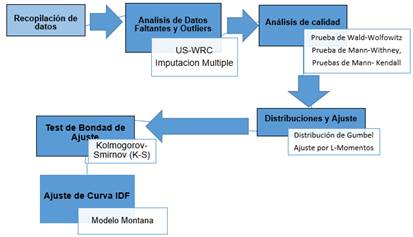
Posteriormente, se estiman los parámetros de la distribución de Gumbel utilizando el procedimiento de los L-momentos, siendo este el más sencillo, pues requiere obtener de la muestra los estimadores de tantos momentos como parámetros tenga el modelo de distribución. Se continúa con la prueba de bondad de ajuste de Kolmogorov-Smirnov por su capacidad de suponer de manera razonable, que las observaciones pudieran corresponder a la distribución específica, es fácil de calcular y usar, y no requiere agrupación de los datos para lograr finalmente ajustar las curvas IDF al modelo de Montana. El procedimiento descrito con anterioridad supone un orden lógico para el desarrollo de la investigación, expresado en la figura 1, considerándose un esquema tecnológico fomentado por varias metodologías ya existentes.
Ubicación geográfica
Caibarién se sitúa en la costa Norte de la provincia de Villa Clara, en la zona central de Cuba. Presenta un clima tropical, al igual que el resto del territorio nacional cuya frontera marítima son los mares tropicales. Las brisas del mar suavizan el clima de la ciudad, lo cual se ve reflejado en los elevados valores de humedad del aire, así como la atenuación de las oscilaciones térmicas diarias en la zona costera. El promedio anual de temperatura es de 25,4°C considerándose agosto el mes más cálido y el más frío, enero. La presión atmosférica disminuye en el verano y aumenta en el invierno, también durante el día se presentan variaciones mínimas, más frecuentes en el invierno.
La estación meteorológica Caibarién (Código 78348) se encuentra, específicamente en el municipio de Caibarién (figura 2), situado en la costa noreste de Villa Clara, localizada en la latitud 22º 29' 48.3" N y longitud 79º 28' 13.3" W con una elevación de 46.27 metros sobre el nivel medio del mar. Fue fundada, el 1ro de agosto de 1987 y se clasifica dentro de la zona rural, con una capacidad manual y automática de captación de datos meteorológicos y la disposición de varios instrumentos adecuados a la actividad meteorológica, entre los cuales se encuentra el pluviómetro y pluviógrafo.
 Fuente: INSMET
Fuente: INSMETFig. 2 Ubicación geográfica de la Estación Meteorológica Caibarién, provincia de Villa Clara, Cuba.
Recopilación de datos y procesamiento de la Información
Para la obtención de las series de intensidades máximas de la estación meteorológica de Caibarién se cuenta con un máximo de 30 años recopilados. Para ello se acudió al Instituto de Meteorología de la Provincia de Villa Clara (INSMET), donde amablemente proporcionaron las cartas pluviográficas mostradas en la figura 3 para su posterior digitalización. Como resultado, se obtuvo la información disponible de los registros de lluvias del pluviógrafo en el período de 1990 a 2019, los cuales fueron transcritos en una hoja de cálculo de Excel.
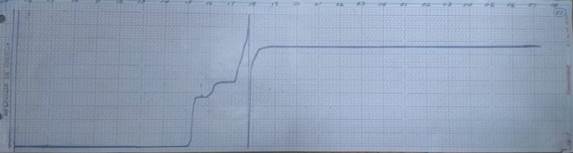
Fig. 3 Carta pluviográfica obtenida de la Estación Meteorológica Caibarién, provincia de Villa Clara, Cuba.
De toda la información recopilada se debe generar una tabla con la Serie de Máximos Anuales (SMA) definiéndose como una serie de datos de valores máximos o una instancia extrema con duración crítica para cada año, independientemente de la magnitud de los valores, determinándose el número de valores en un SMA siempre igual al número de años de registro y manteniendo una estrecha relación entre los períodos de retornos (Ec.1).
El período de retorno es el lapso de tiempo que se da entre dos aguaceros que presentan una misma magnitud específica, también tiene en cuenta el carácter aleatorio de la lluvia en el tiempo.
Método de imputación múltiple
Para realizar este proceso iterativo y tomar las decisiones más convenientes se utiliza el software SPSS en su versión 25. El procedimiento será la obtención de resultados mediante tres imputaciones aleatorias con Imputación Múltiple (mediante la técnica de regresión lineal) y se escogen los resultados de intensidades máximas más grandes obtenidas en cualquier método, siempre garantizando los siguientes aspectos:
La media de la serie no puede variar significativamente.
La varianza y covarianza deben permanecer constantes con un intervalo de error inferior al 1 %.
Los resultados obtenidos que se pretenden imputar deberán tener un orden lógico de obtención de intensidades en relación con su duración, es decir, las intensidades de 5 min son mayores que las de 10 min y estas, a su vez, mayores que las de 20 min y así consecutivamente.
El procedimiento combina distintos estimadores generados a partir de m imputaciones. Utilizando la notación, se considera una variable Q̂ y U el estimador de su varianza. Después de generar m conjuntos de datos mediante simulaciones, se tienen m estimadores de Q̂ y de U (Medina et al., 2007).
Existen dos componentes de la varianza de Q̂. La varianza de cada imputación,
Y la varianza entre las imputaciones,
Donde:
Varianza de Q̂ en cada imputación. |
|
Media de las varianzas de Q̂ en todas las imputaciones. |
|
B |
Varianza entre las imputaciones, mide cuánto varían las estimaciones Q̂ entre diferentes conjuntos de datos imputados. |
m |
Número total de conjuntos de datos imputados o el número total de imputaciones realizadas. |
Por tanto, la varianza total (T) se obtiene sumando las expresiones Ec.2 y Ec.3 corrigiendo el número finito de imputaciones por el valor 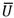 Ec.4
Ec.4
La relación 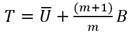 tiene relevancia en el contexto de imputación de datos y proporciona una medida de cuánta información está contenida en los datos faltantes en comparación con los datos observados. La relación
tiene relevancia en el contexto de imputación de datos y proporciona una medida de cuánta información está contenida en los datos faltantes en comparación con los datos observados. La relación 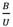 se puede expresar como
se puede expresar como 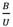 =
= 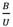 .
.
Donde:
(: es la fracción de datos que está ausente o es faltante.
El intervalo de confianza se obtiene por medio de Ec.5:
Y los grados de libertad de t se calculan como Ec.6 y Ec.7:
Datos anómalos
Para el estudio de outliers se descarta la utilización de los métodos de eliminación y remplazo por su susceptibilidad al sesgo y error humano que impide una replicación o revisión rigurosa, abogando por el método que se basa en el uso de técnicas robustas como es el caso del US-WRC recomendado por (Ng et al., 2007) y utilizado en Estados Unidos.
Este método se basa en el principio de la prueba de hipótesis con el supuesto subyacente de log Pearson. Para aplicar este método, deben calcularse los logaritmos decimales de los valores de la muestra, y se asume que esta nueva serie sigue una distribución normal. Sobre estas series transformadas, se calcula la media 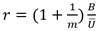 y la desviación típica S
y
, y a continuación, la prueba de datos dudosos US-WRC, presentando las siguientes ecuaciones que demuestran el umbral de datos dudosos Ec.8 y Ec.9:
y la desviación típica S
y
, y a continuación, la prueba de datos dudosos US-WRC, presentando las siguientes ecuaciones que demuestran el umbral de datos dudosos Ec.8 y Ec.9:
Donde Y h y Y l establecen el umbral de dato dudoso alto y bajo respectivamente; K n , es un valor tabulado en función del tamaño de la muestra, con un nivel de significancia del 10 % en información normalmente distribuida; S y , es la desviación estándar y s la desviación típica.
Análisis probabilístico de los resultados
Para que los resultados del estudio se adecuen a la realidad, se deben cumplir los estándares de calidad, por lo que las series de datos deberán satisfacer determinados criterios estadísticos, como los de aleatoriedad, independencia, homogeneidad y estacionalidad definidos por (OMM, 2011) y expuestas a continuación en la Tabla 1, especificándose que son pruebas del tipo paramétricas.
Tabla 1 Tipos de pruebas de calidad de datos.
| Criterios Estadísticos | Prueba recomendada | Intervalo de Confianza en % |
|---|---|---|
| Aleatoriedad | Prueba de Rachas | 95 |
| Independencia | Prueba de Mann-Withney / Wald-Wolfowitz | |
| Estacionalidad | Pruebas de Mann- Kendall |
Prueba de Mann-Kendall
La hipótesis nula (H0) plantea que una muestra de datos ordenados cronológicamente es independiente y está idénticamente distribuida. El estadístico S se define como sigue Ec.10:
Donde:
La prueba de Rachas o Wald-Wolfowitz permite verificar la hipótesis nula de que la muestra es aleatoria, es decir, si las sucesivas observaciones son independientes. Este contraste se basa en el número de rachas que presenta una muestra que proporciona un indicio de si hay o no aleatoriedad en la misma. Un número reducido de rachas es indicio de que las observaciones no se han extraído de forma aleatoria. Los elementos de la primera racha proceden de una población con una determinada característica, mientras que los de la segunda proceden de otra población. De forma idéntica, un número excesivo de rachas puede ser también indicio de no aleatoriedad de la muestra (Castillo et al., 2022).
Si la muestra es suficientemente grande y la hipótesis de aleatoriedad es cierta, la distribución muestral del número de rachas, puede aproximarse mediante una distribución normal de parámetros Ec.11 y Ec.12:
Donde n1 es el número de elementos de una clase; n2 es el número de elementos de la otra clase y n es el número total de observaciones, R es la suma de los rangos de los elementos de la primera muestra de tamaño p en la serie combinada Ec.13.
Para comprobar la independencia de la serie de datos se utiliza la prueba de Mann-Whitney, ya que dicha prueba presenta una distribución de datos libres con el objetivo principal de evaluar la diferencia entre los puntajes de una muestra pequeña medidos en dos momentos diferentes, o sea, sirve para verificar que 2 muestras aleatorias autónomas provienen de dos poblaciones iguales o de una misma población.
La prueba de Mann-Whitney toma en consideración las cantidades siguientes Ec.14 y Ec.15:
Donde V y W son calculados a partir de R, p y q. V representa el número de veces que un ejemplar de la muestra 1 sigue en rango a un ejemplar de la muestra 2; W puede calcularse también de modo análogo para la muestra 2 respecto de la muestra 1 (OMM, 2011) Ec.16.
Y cuya varianza se expresa mediante Ec.17 y Ec.18:
Donde T y j son el número de observaciones ligadas a un rango dado. La suma ΣT abarca todos los grupos de observaciones ligadas de ambas muestras de tamaño p y q.
Una vez que se finalizó el análisis estadístico, se efectúa un ajuste a las distribuciones de probabilidad, teniendo en cuenta que estas son usadas en hidrología para predecir con cierta probabilidad los valores que puede tomar una variable hidrológica.
Para ajustar los valores máximos de precipitación de 5, 10, 20, 40, 60, 90, 120, 150, 240, 300, 720, 1440, 2880 y 4320 minutos para diferentes períodos de retorno, se utiliza la distribución de Gumbel o distribución de Valor Extremo Tipo 1, siendo parte de una familia de distribuciones que nacen de una distribución generalizada de valor extremo (GEV) (Maidment et al., 1994) Ec.19.
Para k = 0 la distribución de Valor Extremo tipo 1 está dada por Ec.320:
Donde u y ( son parámetros de forma y localización, respectivamente.
Los estimadores calculados mediante el método de los momentos son asintóticamente eficientes, en particular al tratarse de distribuciones asimétricas, que son las más usuales en hidrología. Esta eficiencia permite que este método se use en muchos casos como una primera aproximación en la estimación de los parámetros, ya que permite obtener estimaciones de tal modo que los momentos teóricos de una distribución, concuerden con los momentos de la muestra calculados (Acosta Castellanos, 2018) Ec.21 y Ec.22.
Dónde: Sx = Desviación estándar de la muestra 𝑥̅ = Media aritmética de la muestra (Acosta Castellanos, 2018).
Las ecuaciones para su cálculo son Ec.23, Ec.24, Ec.25 y Ec.26:
El momento lineal de primer orden (λ1) es la media de la variable; el segundo momento (λ2) se refiere a la escala de distribución en el que se indica el grado de dispersión de los datos; el momento lineal de tercer orden (λ3) representa la asimetría; por último, el cuarto momento lineal (λ4) se refiere al apuntamiento (también llamado curtosis) que mide cuán escarpada o achatada está la distribución de los datos.
Los estimadores 𝛽 se calculan mediante las expresiones Ec.27, Ec.28 y Ec.29:
Donde n es el número de datos de cada serie; J es el número de orden de cada dato ordenado de menor a mayor; Xjn, es el dato j-ésimo de la serie de n datos.
Para lograr el desarrollo de los aspectos anteriores se pueden complementar la información con las opciones que brinda el software Hidroesta 2, planteándose el siguiente procedimiento:
En la opción distribuciones, escoger la distribución a la cual desea ajustar la SMA.
Se ingresan los datos de manera manual o en las opciones para importar la información de una hoja de excel o access una base datos existentes.
Se define el tipo de ajuste entre parámetros ordinarios y momentos lineales con un nivel de significancia que varía desde el 1 % al 20 %.
Se calcula la serie de datos en la opción calcular para determinar si el delta teórico es menor que el delta tabular y si los datos se ajustan a la distribución escogida con un nivel de significancia determinado.
Para concluir, se introduce el período de retorno en el cual se piensa trabajar y se calcula Q=f (T) para obtener el caudal calculado para dicho periodo de retorno, solo falta emitir un reporte de la información.
Para evitar el uso inadecuado de los estadísticos de prueba, se dispone de la prueba de Kolmogorov-Smirnov determinando si es o no razonable concluir que el conjunto de observaciones dado ha sido obtenido de una familia de distribuciones en particular (OMM, 2011).
Este procedimiento es un test no paramétrico que permite probar si dos muestras provienen del mismo modelo probabilístico. Supóngase que se tienen dos muestras de tamaño total N = m+n compuestas por observaciones x1, x2, x3…, xn e y1, y2, y3…, ym. El test supone que las variables x y y son mutuamente independientes, que cada x proviene de la misma población continua P1 y que las variables y provienen de otra población continua P2. La hipótesis nula es que ambas distribuciones son idénticas, es decir, son dos muestras de la misma población (García, 2022). El test se basa en calcular el estadígrafo J definido como el valor máximo de la diferencia absoluta entre dos funciones de distribución acumulada.
La prueba no precisa que las observaciones sean agrupadas y se usan en cualquier muestra de cualquier tamaño (Maity, 2018), por lo que muestra su superioridad con respecto a la prueba Chi-cuadrado (X2), su facilidad de cálculo ya que no usa una agrupación de datos, además de que el estadístico es independiente de la distribución de frecuencia esperada, solo depende del tamaño de la muestra.
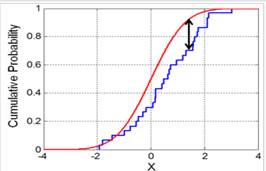
La prueba de bondad de ajuste de Kolmogorov-Smirnov (figura 6) compara el máximo valor absoluto de la diferencia D entre la función de distribución de probabilidad observada F0 (xm) y la estimada F (xm) con un valor crítico (d) que depende del número de datos y el nivel de significancia seleccionado (Zagalo et al., 2020) Ec.30.
Donde F0(Xm) es la función de distribución empírica de la muestra; F(Xm) es la función de distribución teórica de la población que se quiere contrastar y D es el estadístico definido en la expresión.
Si D < d, se acepta la hipótesis nula, es decir, se acepta la función de distribución de probabilidad. Para esta prueba, la función de distribución de probabilidad observada se calcula mediante Ec.31:
Donde m es el número de orden del dato Xm en una lista de mayor a menor y n es el número total de datos.
Ajuste de Curvas IDF
Los resultados del análisis de frecuencias se expresan generalmente en términos de las relaciones intensidad-duración-frecuencia en un lugar dado, o se exponen en forma de atlas de frecuencia de precipitación, en los que se indican las alturas acumuladas de precipitación de lluvia para distintas duraciones y períodos de retorno en la región de interés (OMM, 2011).
Sherman (1931) propuso una parametrización que en la actualidad se adopta en todo el mundo, siendo la representación matemática y gráfica del cálculo de curvas IDF. Esta formulación es una ecuación racional del tipo Ec.32:
El numerador P(T) es función del período de retorno (T) e indica el cuantil para la frecuencia acumulada (1-1/T) de una función de distribución de probabilidad de una variable aleatoria. Luego según Alfonso et al., (2019), se hicieron estudios donde el denominador que es en función del tiempo, se admite que puede expresarse como un polinomio que permite factorización, comúnmente llamado factor de escala y queda la siguiente parametrización general Ec.33:
Donde 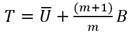 es la intensidad media de precipitación de una hora y período de retorno de T años; d es la duración e
es la intensidad media de precipitación de una hora y período de retorno de T años; d es la duración e 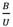 es la intensidad máxima de precipitación para una duración de T (Balbastre Soldevila, 2018).
es la intensidad máxima de precipitación para una duración de T (Balbastre Soldevila, 2018).
Curvas IDF para la estación meteorológica de caibarién
Recopilación de Datos
En colaboración con el Instituto de Meteorología de la Provincia de Villa Clara (INSMET) se obtienen las series de intensidades máximas de la estación meteorológica de Caibarién en un período de 30 años, información disponible de los registros de lluvias del pluviógrafo entre los años de 1990 a 2019, solo produciéndose ausencias de datos en los años 2004, 2012, 2017, 2018 y 2019. De la información obtenida, se logra obtener la serie de máximos anuales en rangos horarios de 5, 10, 20, 40, 60, 90, 120, 150, 240, 300 y 720 y el pluviómetro suministró la información para los rangos horarios de 1440, 2880 y 4320 sin presencia de datos faltantes. (Tabla 2).
Tabla 2 Serie de intensidades de Máximos anuales en rangos horarios de 5, 10, 20, 40, 60, 90, 120, 150, 240, 300,720,1440,2880 y 4320 minutos (muestra).
| Año | 5 min | 10 min | 20 min | 40 min | 60 min | 90 min | 120 min | 150 min | 240 min | 300 min | 720 min | 1440 min | 2880 min | 4320 min |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1990 | 2,0 | 2,0 | 1,42 | 1,17 | 0,96 | 0,67 | 0,51 | 0,40 | 0,25 | 0,20 | 0,09 | 0,04 | 0,03 | 0,02 |
| 1991 | 2,33 | 2,00 | 1,50 | 1,13 | 0,85 | 0,64 | 0,48 | 0,39 | 0,27 | 0,24 | 0,09 | 0,05 | 0,04 | 0,03 |
| 1992 | 1,67 | 1,20 | 1,00 | 0,96 | 0,71 | 0,51 | 0,40 | 0,33 | 0,21 | 0,17 | 0,09 | 0,05 | 0,03 | 0,03 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 2011 | 2,00 | 1,84 | 1,50 | 1,04 | 0,78 | 0,57 | 0,48 | 0,39 | 0,25 | 0,22 | 0,13 | 0,07 | 0,06 | 0,04 |
| 2012 | 0,09 | 0,05 | 0,04 | |||||||||||
| 2013 | 2,00 | 1,84 | 1,45 | 0,94 | 0,86 | 0,60 | 0,46 | 0,37 | 0,24 | 0,21 | 0,17 | 0,06 | 0,05 | 0,03 |
| 2014 | 2,00 | 2,00 | 1,75 | 1,24 | 0,87 | 0,67 | 0,57 | 0,46 | 0,29 | 0,23 | 0,10 | 0,05 | 0,03 | 0,02 |
| 2015 | 2,00 | 2,00 | 1,50 | 1,25 | 0,96 | 0,66 | 0,51 | 0,42 | 0,28 | 0,23 | 0,44 | 0,05 | 0,03 | 0,02 |
| 2016 | 2,00 | 1,50 | 1,25 | 0,91 | 0,76 | 0,67 | 0,58 | 0,49 | 0,33 | 0,26 | 0,13 | 0,07 | 0,04 | 0,02 |
| 2017 | 0,24 | 0,15 | 0,10 | |||||||||||
| 2018 | 0,10 | 0,10 | 0,09 | |||||||||||
| 2019 | 0,07 | 0,04 | 0,04 |
Datos faltantes
Diferentes factores que influyen en la pérdida de datos o la inexistencia de estos, en la estación pluviográfica se ven afectados los años 2004, 2012, 2017, 2018 y 2019, por lo que no se logran obtener los valores de intensidades máximas anuales de la lluvia. Para revelar las carencias provocadas por estos datos ausentes, se utiliza el método de Imputación múltiple con ayuda del software estadístico SPSS, con un máximo de 30 iteraciones obteniendo, a criterio del autor, los promedios para cada año faltante se muestran en la tabla 3.
Tabla 3 Resultados de la imputación de valores a los datos faltantes de los años 2004, 2012, 2017, 2018 y 2019 para duraciones de 5, 10, 20, 40, 60, 90, 120, 150, 240, 300 y 720 minutos.
| Tiempo | Valores Imputados 2004 | Valores Imputados 2012 | Valores Imputados 2017 | Valores Imputados 2018 | Valores Imputados 2019 |
|---|---|---|---|---|---|
| 5 min | 2,275 | 1,659 | 2,104 | 1,755 | 1,592 |
| 10 min | 1,917 | 1,486 | 1,808 | 1,538 | 1,415 |
| 20 min | 1,529 | 1,267 | 1,464 | 1,279 | 1,241 |
| 40 min | 1,163 | 0,938 | 1,101 | 0,939 | 0,882 |
| 60 min | 0,908 | 0,709 | 0,857 | 0,701 | 0,725 |
| 90 min | 0,691 | 0,522 | 0,644 | 0,505 | 0,503 |
| 120 min | 0,553 | 0,419 | 0,513 | 0,417 | 0,411 |
| 150 min | 0,454 | 0,339 | 0,419 | 0,338 | 0,332 |
| 240 min | 0,317 | 0,215 | 0,280 | 0,220 | 0,221 |
| 300 min | 0,254 | 0,173 | 0,229 | 0,179 | 0,184 |
| 720 min | 0,169 | 0,166 | 0,144 | 0,172 | 0,200 |
Datos Anómalos
La aplicación del método US-WRC (figura 7) muestra como ninguno de los datos a comprobar (línea azul) supera el límite superior (línea naranja) arrojando como resultado una ausencia total de datos anómalos en la serie de datos.
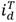
Fig. 7 Gráfica representativa del método US-WRC para una duración de 5 min. Fuente: Elaboración propia.
Calidad de datos
Los resultados de las pruebas de calidad aplicadas a las series de máximos anuales, Rachas, Mann-Whitney (M-W), Wald-Wolfowitz (W-W) y Mann-Kendall (M-K) se resumen de la forma siguiente:
Las series son aleatorias para un nivel de significancia del 5 % (Prueba de Rachas /W-W).
Las series son independientes para un nivel de significancia del 5 % (Pruebas M-W).
Las series son estacionales para un nivel de significancia del 5 % (Prueba de M-K).
Luego de realizar el estudio y comprobar que todas las series son estacionales, se investiga sobre las tendencias de dichas series, para ello se grafican los resultados observados en la figura 8 demuestran que las series datos para la elaboración de las curvas IDF de la estación meteorológica de Caibarién, son aptas para su procesamiento probabilístico, destacando que se pueden usar modelos estacionarios para su representación, sin necesidad de acudir a modelos no estacionarios.
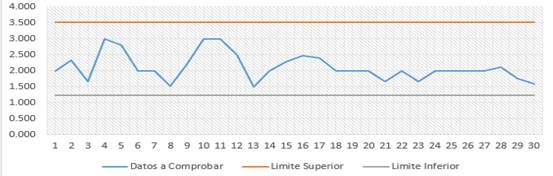
Fig. 8 Análisis de tendencia para la serie de 5 minutos cuya pendiente fue de las más elevadas de las series estudiadas.
Los resultados obtenidos de las diferentes pruebas de calidad demuestran que las series datos para la elaboración de las curvas IDF de la estación meteorológica de Caibarién, son aptas para su procesamiento probabilístico.
Distribución de probabilidad
La Tabla 4 muestra los resultados de los parámetros de posición y escala obtenidos del análisis de distribución de Gumbel (ξ=0) con ajuste por L-momentos para 5, 10, 20, 40, 60, 90, 120, 150, 240, 300, 720, 1440, 2880 y 4320 minutos.
Tabla 4 Parámetros de la distribución de probabilidad de Gumbel obtenidos para las series de 5, 10, 20, 40, 60, 90, 120, 150, 240, 300, 720, 1440, 2880 y 4320 minutos.
| Serie | Parámetro de posición | Parámetro de Escala |
|---|---|---|
| 5 min | 1,9018 | 0,4357 |
| 10 min | 1,6404 | 0,3422 |
| 20 min | 1,3449 | 0,255 |
| 40 min | 0,9833 | 0,2405 |
| 60 min | 0,7655 | 0,1884 |
| 90 min | 0,5731 | 0,15 |
| 120 min | 0,3694 | 0,1077 |
| 150 min | 0,3694 | 0,1077 |
| 240 min | 0,2416 | 0,0833 |
| 300 min | 0,1971 | 0,0676 |
| 720 min | 0,1116 | 0,055 |
| 1440 min | 0,0621 | 0,0287 |
| 2880 min | 0,0411 | 0,0196 |
| 4320 min | 0,0307 | 0,0139 |
Test de bondad de ajuste de Kolmorogov-Smirnov.
Para la obtención de la función de probabilidad de mejor ajuste se realiza el test de bondad de ajuste de Kolmorogov-Smirnov lo cual, como el delta teórico, es menor que el delta tabular los datos se ajustan a la distribución Gumbel, con un nivel de significación del 5 %. (Tabla 5)
Tabla 5 Prueba de Kolmorogov-Smirnov desarrollada en el software Hidroesta 2.
| M | X | P(X) | G(Y)Ordinario | G(Y) Mom Lineal | Delta |
|---|---|---|---|---|---|
| 1 | 1,0 | 0,0323 | 0,0031 | 0,0004 | 0,0291 |
| 2 | 1,52 | 0,0645 | 0,1329 | 0,0905 | 0,0684 |
| 3 | 1,6 | 0,0968 | 0,1745 | 0,1304 | 0,0778 |
| 4 | 1,66 | 0,129 | 0,2176 | 0,1743 | 0,0886 |
| 5 | 1,67 | 0,1613 | 0,2252 | 0,1823 | 0,064 |
| 6 | 1,67 | 0,1935 | 0,2252 | 0,1823 | 0,0317 |
| 7 | 1,75 | 0,2258 | 0,285 | 0,2465 | 0,0592 |
| 8 | 2,0 | 0,2581 | 0,4652 | 0,4501 | 0,2071 |
| 9 | 2,0 | 0,2903 | 0,4652 | 0,4501 | 0,1749 |
| 10 | 2,0 | 0,3226 | 0,4652 | 0,4501 | 0,1426 |
| 11 | 2,0 | 0,3548 | 0,4652 | 0,4501 | 0,1104 |
| 12 | 2,0 | 0,3871 | 0,4652 | 0,4501 | 0,0781 |
| 13 | 2,0 | 0,4194 | 0,4652 | 0,4501 | 0,0459 |
| 14 | 2,0 | 0,4516 | 0,4652 | 0,4501 | 0,0136 |
| 15 | 2,0 | 0,4839 | 0,4652 | 0,4501 | 0,0187 |
| 16 | 2,0 | 0,5161 | 0,4652 | 0,4501 | 0,0509 |
| 17 | 2,0 | 0,5484 | 0,4652 | 0,4501 | 0,0832 |
| 18 | 2,0 | 0,5806 | 0,4652 | 0,4501 | 0,1154 |
| 19 | 2,0 | 0,6129 | 0,4652 | 0,4501 | 0,1477 |
| 20 | 2,1 | 0,6452 | 0,5377 | 0,5331 | 0,1075 |
| 21 | 2,2 | 0,6774 | 0,6230 | 0,6039 | 0,0775 |
| 22 | 2,28 | 0,7097 | 0,6447 | 0,6541 | 0,065 |
| 23 | 2,33 | 0,7419 | 0,6751 | 0,6878 | 0,0668 |
| 24 | 2,4 | 0,7742 | 0,7110 | 0.7271 | 0,0632 |
| 25 | 2,46 | 0,8065 | 0,7401 | 0.7585 | 0,0663 |
| 26 | 2,49 | 0,8387 | 0,7559 | 0.7753 | 0,0828 |
| 27 | 2,79 | 0,871 | 0,8584 | 0.8720 | 0,0125 |
| 28 | 3,0 | 0,9032 | 0,9035 | 0.9227 | 0,0030 |
| 29 | 3,0 | 0,9355 | 0,9035 | 0.9227 | 0,032 |
| 30 | 4,67 | 0,9677 | 0,9965 | 0,9982 | 0,0288 |
Ajuste a una función paramétrica IDF
La aplicación del modelo Montana para el ajuste de las intensidades de la serie de máximos anuales de la estación meteorológica del Caibarién se resumen en la tabla 6 y los valores de k, m, θ, C y n se expresan en la tabla 7 obtenidos en el Software Matlab.
Tabla 6 Valores del modelo Montana.
| Tiempo (min) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 años | 5 | 10 | 20 | 40 | 60 | 90 | 120 | 150 | 240 | 300 | 720 | 1440 | 2880 | 4320 |
| 2,13 | 1,86 | 1,50 | 1,10 | 0,88 | 0,68 | 0,56 | 0,48 | 0,34 | 0,28 | 0,16 | 0,09 | 0,05 | 0,04 | |
| 3 años | 2,27 | 1,98 | 1,60 | 1,17 | 0,94 | 0,73 | 0,60 | 0,51 | 0,36 | 0,30 | 0,17 | 0,09 | 0,06 | 0,05 |
| 5 años | 2,46 | 2,14 | 1,73 | 1,27 | 1,02 | 0,79 | 0,65 | 0,55 | 0,39 | 0,33 | 0,19 | 0,10 | 0,07 | 0,05 |
| 10 años | 2,74 | 2,39 | 1,93 | 1,42 | 1,14 | 0,88 | 0,73 | 0,62 | 0,43 | 0,36 | 0,22 | 0,12 | 0,08 | 0,06 |
| 20 años | 3,06 | 2,66 | 2,15 | 1,58 | 1,27 | 0,98 | 0,81 | 0,69 | 0,48 | 0,41 | 0,26 | 0,14 | 0,09 | 0,07 |
| 25 años | 3,17 | 2,76 | 2,23 | 1,64 | 1,31 | 1,02 | 0,84 | 0,71 | 0,50 | 0,42 | 0,28 | 0,15 | 0,10 | 0,08 |
| 30 años | 3,26 | 2,84 | 2,29 | 1,69 | 1,35 | 1,05 | 0,86 | 0,74 | 0,52 | 0,43 | 0,29 | 0,16 | 0,10 | 0,08 |
| 50 años | 3,53 | 3,08 | 2,48 | 1,83 | 1,46 | 1,14 | 0,93 | 0,80 | 0,56 | 0,47 | 0,32 | 0,18 | 0,11 | 0,09 |
| 75 años | 3,76 | 3,28 | 2,65 | 1,95 | 1,56 | 1,21 | 1,00 | 0,85 | 0,60 | 0,50 | 0,35 | 0,19 | 0,12 | 0,10 |
| 100 años | 3,93 | 3,43 | 2,77 | 2,04 | 1,63 | 1,27 | 1,04 | 0,89 | 0,62 | 0,52 | 0,38 | 0,21 | 0,13 | 0,10 |
Tabla 7 Valores de k, m, θ, y m
| Parámetros a Estimar | Menores de 360 min | Mayores de 360 min |
|---|---|---|
| C | 20.49 | 6.57 |
| θ | 0.90 | 0.35 |
| k | 47.20 | 0.42 |
| m | 0.16 | 0.22 |
Se grafican las curvas IDF obtenidas con el modelo de Montana y para profundizar más en el comportamiento del modelo se hace necesario convertir las curvas IDF en curvas de Precipitación-Duración-Frecuencia (PDF) con lo cual se puede obtener el residuo del modelo y se puede apreciar con claridad el rango de validez del mismo. En la Figuras 9 y 10 se muestra un gráfico donde se muestra el modelo de Montana ajustado a los datos obtenidos por el modelo probabilístico de Gumbel para valores menores y mayores de 360 minutos respectivamente.
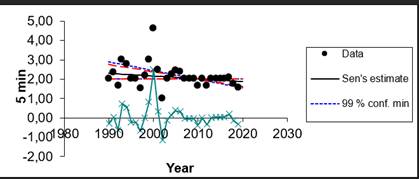
Fig. 9 Modelo de Montana ajustado a los datos obtenidos por el modelo probabilístico de Gumbel para menores de 360 minutos.
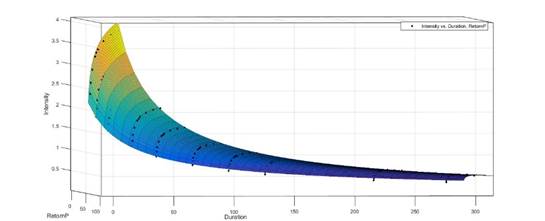
Fig. 10 Modelo de Montana ajustado a los datos obtenidos por el modelo probabilístico de Gumbel para mayores de 360 minutos.
Comparación de resultados con la NC 1239-2018
Los resultados obtenidos se sometieron a una comparación con la NC 1239-2018 para observar las diferencias por exceso entre cada una, arrojando los siguientes resultados en la Figura 11 y 12.
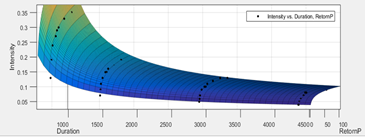
Fig. 11 Diferencia de los resultados obtenidos y la NC 1239-2018 para duraciones menores de 40 minutos.
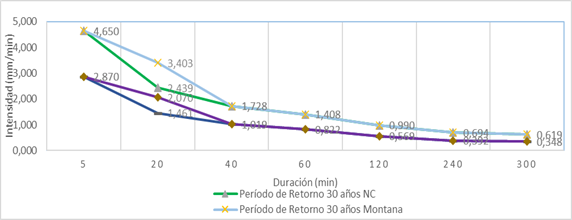
Fig. 12 Diferencia de los resultados obtenidos y la NC 1239-2018 para duraciones mayores de 40 minutos. 720, 1440,2880 y 4320
Conclusiones
Se desarrolló un análisis de formas de proceder en estudios similares a nivel nacional e internacional que permitió determinar la mejor metodología a aplicar en la realización de curvas IFD, definiendo la calidad del resultado, ya que la misma abarca un amplio conjunto de métodos analíticos y matemáticos.
Se define un diagrama de flujo de trabajo a aplicar para la elaboración en este tipo de investigación que sirve de precedente para estudios similares en la provincia.
Se aplicaron técnicas estadísticas para comprobar la bondad de ajuste y la calidad de la serie de datos, logrando satisfacer determinados criterios estadísticos como los de aleatoriedad, independencia y estacionalidad.
Los resultados de esta investigación expresan datos desarrollados a través del método de Montana que al ser comparados con la NC 1239-2018.