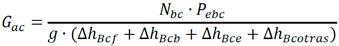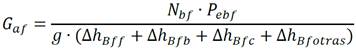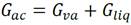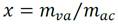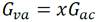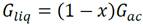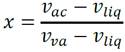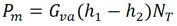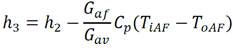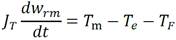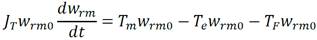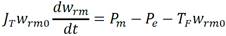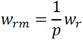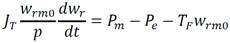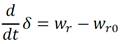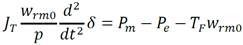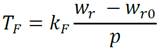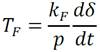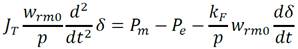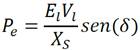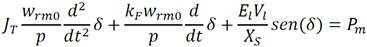Introducción
La Conversión de Energía Térmica Oceánica, OTEC (Ocean Thermal Energy Conversion, del inglés), o energía maremotérmica es una fuente renovable de energía basada en el cambio de la temperatura del mar respecto a la profundidad, este gradiente de temperatura se puede utilizar para impulsar una máquina térmica que genera trabajo útil que se convierte en electricidad. Los océanos captan el calor generado por la radiación solar por lo cual los sistemas OTEC son una fuente de energía casi ilimitada dependiente del sol. (Heredia et al. 2023).
El escritor francés Julio Verne, en su obra Veinte mil leguas de viaje submarino, publicada en 1869, fue la primera persona en hacer referencia a la obtención de energía eléctrica a partir del gradiente de temperatura de los océanos. En el año 1881 el físico francés Jacques Arsene d’Arsonval propuso esta tecnología. (Heredia et al. 2023) El 22 de noviembre de 1926 el ingeniero francés Georges Claude presentó a la Academia de Ciencias de París un modelo, a escala, que demostraba la posibilidad de aprovechar la energía maremotérmica. Este científico en el año 1930 construyó en Cuba, al norte de Matanzas, la primera central maremotérmica del mundo como se muestra en la figura 1, que funcionó 11 días, pues fue destruida por una tempestad, luego construyó otra en aguas de Río de Janeiro (1934-1935). Aunque estas centrales demostraron la viabilidad del proyecto de Claude, acabaron en fracaso a causa de los efectos del movimiento del oleaje sobre la conducción sumergida (Abreu 2021) y (Heredia et al. 2023)
 (Diario de la época, Matanzas, 1930)
(Diario de la época, Matanzas, 1930)Fig. 1 Primera planta piloto del mundo para la explotación de la energía maremotérmica en Cuba.
En la última década se han realizados varios proyectos de plantas OTEC como los proyectos propuestos por la empresa estadounidense Ocean Thermal Energy Corporation, para construir dos plantas OTEC de 5 y 10 MW en las Islas Marshall, y en la base naval de Diego García en el Océano Índico construir una planta OTEC de 13 MW para sustituir los actuales generadores diésel. De igual modo en las Bahamas se han proyectado dos plantas maremotérmicas de 5 y 10 MW que serían explotadas en modo de concesión por la compañía americana Ocean Thermal Energy Corporation. Actualmente se encuentra en operación la planta OTEC más grande del mundo situada en la costa de Kona, en Hawái, Estados Unidos, las aguas tropicales de la región presentan grandes diferencias de temperatura, existen profundidades notables en zonas cercanas a la costa donde la temperatura puede bajar hasta los 5 (C en el fondo del mar. (Heredia et al. 2023).
De las cinco formas de obtener energía de los mares, solo es posible la explotación de tres de ellas en los mares aledaños a Cuba, estas son: energía de las corrientes de marea, energía de las olas (Undimotriz) y el gradiente de energía térmica del océano, según (Lorenzo et al. 2023) y (Castellano et al. 2022). El objetivo de este trabajo es modelar matemáticamente centrales maremotérmicas de ciclo abierto o de Anderson emplazadas en la costa y conectadas al sistema eléctrico en MatLab/Simulink®. Luego, se emplea el modelo para determinar, en un escenario, la potencia producida por el generador y la entregada al sistema eléctrico. Los autores usan el esquema de Anderson por ser el adecuado para Cuba según la comparación de OTECs reportada en (Heredia et al. 2023).
Funcionamiento del esquema del sistema de ciclo abierto o ciclo de Anderson
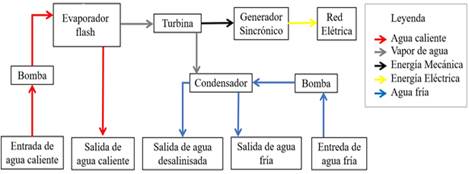
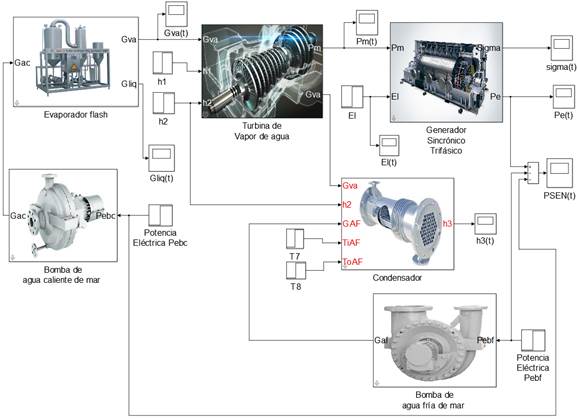
El diagrama funcional de centrales maremotérmicas de ciclo abierto o de Anderson conectadas al sistema eléctrico y emplazadas en costa, obtenido por los autores, se muestra en la figura 2. En este se observa que la bomba de agua caliente impulsa el fluido, agua caliente del mar, hacia el evaporador flash que convierte parte del agua en vapor y el agua líquida la devuelve al mar; el vapor de agua cede energía a la turbina y esta constituye la fuente motriz del generador eléctrico que aporta energía a la red eléctrica; luego que el vapor realiza trabajo en la turbina fluye al condensador intercambiando calor con el agua fría de mar bombeada por la bomba de agua fría y al condensarse esta puede emplearse para el riego y otras actividades. Ishaq y Dincer (2020) y (Heredia et al. 2023).
Modelado de centrales maremotérmicas de Anderson conectadas a la red eléctrica y emplazada en tierra o en costa.
La modelación matemática de plantas maremotérmicas de ciclo abierto o de Anderson conectadas al Sistema Electroenergético Nacional (SEN) y emplazadas en tierra, parte de aplicar las leyes de Newton a la dinámica rotacional y la Termodinámica. Los componentes principales del diagrama funcional mostrado en la figura 2 son: las bombas de agua caliente y fría de mar, el evaporador flash, la turbina y el generador eléctrico conectado al SEN.
Bomba de agua caliente de mar
El modelo matemático para la bomba de agua caliente de mar está basado en el reportado en (Gil 2017), donde los autores despejaron el flujo másico de agua caliente en función de la potencia suministrada a la bomba. Esto se corresponde con el proceso real, se suministra potencia a la bomba para lograr un flujo másico.
Donde: G ac flujo másico de agua caliente de mar en kg/s; N bc eficiencia de la bomba de agua caliente, adimensional; P ebc potencia eléctrica de la bomba de agua caliente en W; g aceleración de la gravedad en m/s2; ∆h Bcf pérdida de carga debida a los tramos rectos de tubería en m; ∆h Bcb pérdida de carga debida a la curvatura de la tubería en m; ∆h Bce pérdida de carga en el evaporador en m; y ∆h Bcotras representa otras pérdidas en m, esta variable fue adicionada por los autores para permitir a un investigador incorporar otras pérdidas posibles de una planta específica que no esté contemplada en la ecuación dada en (Gil 2017).
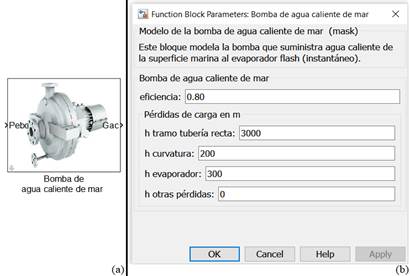
A modo de ejemplo, se tiene para la bomba SNZ/SEZ una eficiencia de 0,80 según (Gil 2017). En la figura 3 a) se muestra el bloque en MatLab/Simulink® donde se implementó la ecuación (1) y la figura 3 b) muestra la interfaz de diálogo creada para dicho bloque.
 (Fuente: el autor)
(Fuente: el autor)Figura 3 (a) Bloque que modela la bomba de agua caliente de mar, (b) ventana de entrada de parámetros.
Bomba de agua fría de mar
De modo semejante, al modelo de la bomba de agua caliente, se operó con el modelo matemático para la bomba de agua fría de mar en la expresión reportada en (Gil 2017).
Donde: G af flujo másico de agua fría de mar en kg/s; N bf eficiencia de la bomba de agua fría, adimensional; P ebf potencia eléctrica de la bomba de agua fría, en W; g aceleración de la gravedad en m/s2; ∆h Bff pérdida de carga debida a los tramos rectos de tubería de agua fría en m; ∆h Bfb pérdida de carga debida a la curvatura de la tubería de agua fría en m; ∆h Bfc pérdida de carga en el condensador en m; y ∆h Bfotras representa otras pérdidas en m, de modo similar al caso de la bomba de agua caliente, los autores adicionaron la variable ∆h Bfotras para permitir a un investigador incorporar otras pérdidas.
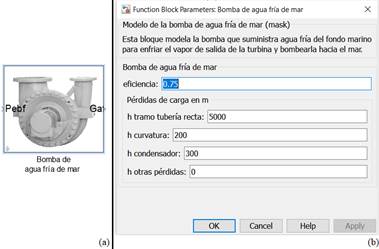
Según se reporta en (Gil 2017) una bomba para el agua fría de mar tiene una eficiencia de 0,75. En la figura 4 a) se muestra el bloque en MatLab/Simulink( donde se implementó la ecuación (2) y la figura 4 b) muestra la interfaz de diálogo creada para dicho bloque.
 (Fuente: el autor)
(Fuente: el autor)Figura 4 (a) Bloque que modela la bomba de agua fría de mar, (b) ventana de entrada de parámetros.
Evaporador flash
Es el equipo en el cual ocurre la evaporación casi instantánea de un líquido por disminución brusca de la presión según Green and Southard (2019). Este dispositivo evapora parte del agua caliente de mar en la cámara de evaporación y tiene como residuo la parte no evaporada con mayor concentración de sales denominada salmuera útil para la acuicultura según (Vera et al. 2020). El parámetro de operación del evaporador flash es la presión en la cámara de vacío, la que es inferior a la presión atmosférica. Para determinar la expresión matemática que relaciona los flujos másicos del agua caliente a la entrada del evaporador y los del vapor y de salmuera a la salida de este, se aplica un balance de masa según Green and Southard (2019), del cual se obtiene la ecuación (3).
Donde: G ac flujo másico de agua caliente de mar a la entrada del evaporador en kg/s, G va flujo másico de vapor de agua a la salida del evaporador en kg/s, G liq flujo másico de salmuera a la salida del evaporador en kg/s. Es válido mencionar que G ac es suministrado al evaporador flash por la bomba de agua caliente.
En (Green and Southard, 2019) se determina la fracción de vapor, denominada título, que se obtiene al disminuir bruscamente la presión a la masa de agua caliente mediante la expresión siguiente:
donde: x es el título, adimensional; m va masa de vapor a la salida del evaporador en kg, m ac masa de agua caliente de mar a la entrada del evaporador en kg/s. De (Green and Southard, 2019) se conoce que G ac = dm va /dt y G ac = dm ac /dt luego junto a las ecuaciones (3) y (4) se determinan los flujos másicos a la salida del evaporador en función del título y del flujo másico a la entrada del evaporador como muestran las siguientes ecuaciones: (5) y (6)
El cálculo de x, según Green and Southard (2019), se realiza mediante la siguiente expresión (7):
Donde: v ac volumen específico del agua caliente de mar a la entrada del evaporador en m3/kg; v va volumen específico del vapor a la salida del evaporador en m3/kg; v liq volumen específico del agua líquida o salmuera a la salida del evaporador en m3/kg. Los volúmenes v va y v liq son funciones de la presión en la cámara de vacío.
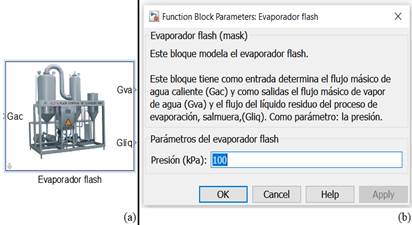
En la figura 5 a) se muestra el bloque en MatLab/Simulink( donde se implementaron las ecuaciones (5), (6) y (7) y la figura 5 b) muestra la interfaz de diálogo creada para dicho bloque.
 (Fuente: el autor)
(Fuente: el autor)Figura 5 (a) Bloque que modela el evaporador flash, (b) ventana de entrada del parámetro presión.
Turbina
La turbina de vapor funciona con la energía que posee el fluido de trabajo, energía que es cedida a los álabes de la turbina y transmitida por su eje. De esta forma la turbina obtiene la energía mecánica para mover el rotor de un generador eléctrico y que este produzca energía eléctrica. La potencia de la turbina se calcula según (Gil 2017) con la siguiente ecuación:
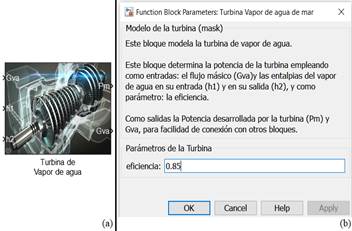
Donde: P m potencia motriz desarrollada por la turbina en W; G va flujo másico de vapor de agua en kg/s; h 1 entalpía del vapor de agua a la entrada de la turbina en J/kg; h 2 entalpía del vapor de agua a la salida de la turbina en J/kg; N T eficiencia de la turbina, adimensional. En la figura 6 a) se muestra el bloque en MatLab/Simulink( donde se implementó la ecuación (8) y la figura 6 b) muestra la interfaz de diálogo creada para dicho bloque.
 (Fuente: el autor)
(Fuente: el autor)Figura 6 (a) Bloque que modela la turbina, (b) ventana de entrada del parámetro eficiencia de la turbina.
Condensador
Un condensador, en termodinámica, es un equipo intercambiador de calor, que pretende que el fluido gaseoso, fluido caliente, que lo recorre cambie a fase líquida mediante el intercambio de calor, con otro medio, fluido enfriador (Cortés 2020). La expresión matemática que modela al condensador es dada en (Gil 2017) y se muestra en la ecuación (9).
Donde: h 3 entalpía del agua caliente a la salida del condensador en J/kg, h 2 entalpía del vapor de agua a la entrada del condensador en J/kg, G av flujo másico del vapor de agua en kg/s, G af flujo másico de agua fría de mar en kg/s, C p capacidad calorífica específica del agua de mar en J/kg(C, T iAF temperatura del agua de mar a la entrada del condensador en (C, T oAF temperatura del agua de mar a la salida del condensador en (C.
Se remarca que se empleó el símbolo h 2 para la entalpía del vapor de agua tanto a la entrada del condensador como a la salida de la turbina, debido a que el vapor que sale de la turbina es el mismo que entra al condensador, como se aprecia en el diagrama funcional mostrado en la figura 2.
En la figura 7 a) se muestra el bloque en MatLab/Simulink( donde se implementó la ecuación (9) y la figura 7 b) muestra la interfaz de diálogo creada para dicho bloque.
 (Fuente: el autor)
(Fuente: el autor)Figura 7 (a) Bloque que modela el condensador, (b) ventana de entrada del parámetro capacidad calorífica.
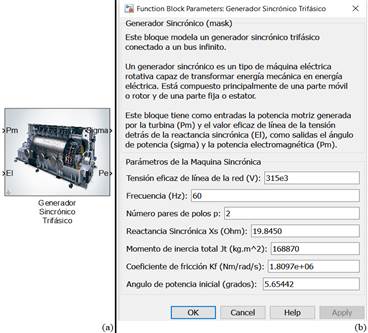
Generador Síncrono
Un generador síncrono es una máquina eléctrica rotatoria que convierte la energía mecánica en energía eléctrica. Éste se compone de: rotor o excitación y estator o armadura. El rotor es la parte móvil del generador, mientras que el estator es la parte fija según (Fitzgerald 1996). La razón por la que se llama generador síncrono es la igualdad entre la velocidad del campo sincrónico y la velocidad angular del rotor, es decir, el rotor girará a la velocidad del campo magnético sincrónico, en estado estacionario, lo cual se denomina sincronismo (Fitzgerald 1996). El generador eléctrico se supone que está conectado al SEN, el cual se considera un bus de potencia infinita, según criterio dado en (Fitzgerald 1996). Aplicando la segunda Ley de Newton al movimiento rotacional, según (Fitzgerald 1996), se tiene:
Donde: J T momento de inercia total del grupo turbina-generador eléctrico en kgm2, w rm velocidad angular del rotor del generador en rad/s, T m torque motriz desarrollado por la turbina en Nm, T e torque electromagnético del generador eléctrico en Nm, T F torque de amortiguamiento en Nm.
Para relacionar los torques con las potencias se multiplica la ecuación (10) por la velocidad sincrónica del rotor, w rm0 , bajo el supuesto de pequeñas desviaciones de w rm alrededor de w rm0 . De lo anterior se obtiene ecuación (11):
Al aplicar las expresiones siguientes: P m = T m w rm0 y P e = T e w rm0 , se obtiene la ecuación (12).
De (Fitzgerald 1996) se conoce que la velocidad instantánea del rotor en rad geométricos por segundo, w rm , se relaciona con la velocidad instantánea del rotor en rad eléctricos por segundo, w r , y el número de pares de polos del generador, p, mediante la ecuación (13).
Sustituyendo en la ecuación (12) la ecuación (13), se obtiene la ecuación (14)
En (Fitzgerald 1996) se define el ángulo de potencia δ en rad eléctricos, como la diferencia de la posición angular de los ejes de los campos magnéticos de excitación, ( r , y de armadura, ( r0 , en radianes eléctricos, o sea, δ =( r - ( r0 . Para relacionar δ con la derivada temporal de w r , se deriva la expresión δ =( r - ( r0 , se recuerda que w r = d( r /dt y se define w r0 = d( r0 /dt, velocidad del campo sincrónico en rad eléctricos por segundo, resultando la ecuación (15).
La interpretación de la ecuación (15), es que la rapidez de cambio de δ es igual a la diferencia de las velocidades angulares instantáneas del rotor y del campo sincrónico, lo cual explica el cambio de posición relativa entre los campos magnéticos de excitación y de armadura. La velocidad del campo de armadura está fijada por la frecuencia de la red eléctrica, para Cuba es 60 Hz. Al despejar w r en la ecuación (15) y al sustituir en la ecuación (14) se tiene:
El torque T F, se relaciona con w r y w r0 a través del coeficiente de fricción debido al amortiguamiento, k F , medido en Nms/rad, (Fitzgerald 1996), como ecuación (17):
Luego, sustituyendo la ecuación (15) en la ecuación (17) se obtiene la ecuación (18).
Al sustituir la ecuación (18) en la ecuación (16) se obtiene la ecuación (19).
Como primera aproximación en este trabajo se emplea para el cálculo de la potencia electromagnética la expresión dada en (Fitzgerald 1996), que se muestra a continuación:
Donde: P e potencia electromagnética en W, E l valor eficaz de la tensión de línea detrás de la reactancia sincrónica en V, V l tensión eficaz de línea de la alimentación en V, X s reactancia sincrónica en (, δ ángulo de potencia en rad eléctricos.
Al sustituir la ecuación (20) en la ecuación (19) y agrupando los términos que contienen al ángulo de potencia en el miembro izquierdo, se obtiene la expresión siguiente:
La ecuación (21) es el modelo del generador eléctrico. Esta presenta la ventaja que además de determinar la potencia eléctrica que el generador produce, obtiene el ángulo de potencia, el cual brinda información acerca de la estabilidad del generador eléctrico. En la figura 8 a) se muestra el bloque en MatLab/Simulink( donde se implementó la ecuación (21) y la figura 8 b) muestra la interfaz de diálogo creada para dicho bloque.
Descripción del modelo en MATLAB/SIMULINK
En la figura 9 se muestra el modelo en MatLab/Simulink( de centrales maremotérmicas de ciclo abierto o de Anderson, conectadas al SEN. Este modelo se ha obtenido mediante la interconexión de los modelos de cada componente según el diagrama funcional de la figura 2.
Como se observa, el modelo de la figura 9 contiene los modelos de cada componente, obtenidos en las subsecciones anteriores. Además, este incluye los bloques visualizadores para graficar señales, las diferentes variables de entrada y salidas cuyos valores brindan información de operación; bloques de entrada de valores, estos facilitan a un investigador implementar varios escenarios; y un bloque sumador para determinar la potencia que la central aporta al SEN, que es menor que la potencia entregada por el generador debido a que el funcionamiento de la planta impone consumir potencia para la alimentación de las bombas de agua fría y caliente.
En esta primera aproximación, realizada en esta investigación, se ha obtenido un modelo que permite flexibilidad a la hora de introducir parámetros y valores de variables, esto facilita a un investigador enfrentar casos de estudios de centrales maremotérmicas de ciclo abierto o de Anderson emplazadas en tierra conectadas al SEN.
Resultados de la ejecución del modelo
Se toma, a manera de caso de estudio, una central emplazada en la costa que se conecta al SEN, red eléctrica trifásica que mediante transformadores en cada fase alimenta a un poblado costero, y se cuentan con los datos para la simulación que se relacionan a continuación:
El generador sincrónico trifásico se conecta a la alimentación trifásica, esta tiene un valor de la tensión eficaz de línea de 190,53 V.
El generador es trifásico de 4 pares de polos, X s de 0,5 ( y k F de 100 Nms/rad. Se alimenta la excitación del generador de modo tal que E l es 225,17 V.
La potencia motriz desarrollada por la turbina es de 80,802 kW, para lo cual la entalpía del vapor de agua a la entrada de esta es de 2 583,9 kJ/kg y a la salida de 1 865,2 kJ/kg.
El evaporador flash opera con una presión de 10 kPa.
La bomba de agua caliente de mar tiene una eficiencia de 0,80 y mueve el fluido superando las siguientes pérdidas de carga, por tubería de tramo recto 3 000 m, por curvatura en la tubería de 200 m y en el evaporador de 300 m. La potencia que consume el motor eléctrico que mueve dicha bomba es 5,600 kW.
La potencia consumida por el motor de la bomba de agua fría es 8,000 kW.
A partir de estos datos se desea responder a las siguientes interrogantes, cuál es el valor de la potencia producida por el generador eléctrico, cuánta potencia esta central es capaz de suministrar al SEN, qué parte es la potencia eléctrica aportada al SEN de la producida por el generador, cuánto es el flujo másico de agua que entrega la bomba de agua caliente de mar y el flujo másico del vapor obtenido por el evaporador.
Para responder a las interrogantes anteriores se emplea el modelo, mostrado en la figura 9, desarrollado en esta investigación en MatLab/Simulink(; se introducen en el modelo los datos anteriores y se ajusta el tiempo de simulación a 3 segundos. Luego de simular el modelo se obtienen los gráficos, que se muestran en la figura 10, con las diferentes variables. Los valores de estas variables a estado estacionario permiten responder las interrogantes.
 (Fuente: el autor)
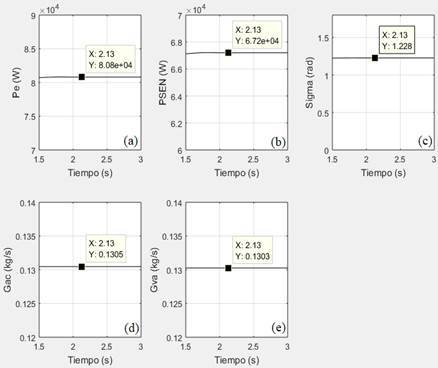
(Fuente: el autor)Figura 10 Gráficas de: (a) potencia eléctrica del generador, (b) potencia suministrada al SEN, (c) ángulo de potencia δ, (d) flujo másico de agua caliente y (e) flujo másico de vapor.
En el gráfico de la figura 10 (a) se observa que la potencia entregada por el generador eléctrico es de 80,800 kW, valor aproximadamente igual a la potencia motriz de la turbina, con un ángulo de potencia de 1,228 rad eléctrico. Esto responde la primera interrogante. De la figura 10 (b) se obtiene que la potencia que la central le entrega al sistema eléctrico es de 67,2 kW, valor menor que la potencia producida por el generador eléctrico, esta diferencia se debe a que en la operación de la planta se consumen 5,600 kW y 8,000 kW por la bomba de agua caliente y la de agua fría respectivamente. Lo anterior indica que para la operación de esta central en las condiciones dadas se necesita 13,600 kW. Esta discusión responde la segunda interrogante. La fracción que representa la potencia aportada al SEN respecto de la entregada por el generador eléctrico, es 67,2 kW entre 80,800 kW aproximadamente igual a 0,83 o el 83%, valor que se considera aceptable. El valor de esta fracción responde a la tercera interrogante. Las respuestas a las interrogantes restantes se obtienen de las gráficas (d) y (e) de la figura 10. Para las condiciones dadas el flujo másico de agua que entrega la bomba de agua caliente de mar es de 0,1305 kg/s y el flujo másico del vapor obtenido por el evaporador es de 0,1303 kg/s. Al comparar los valores de ambos flujos se nota que el evaporador, bajo las condiciones dadas, evapora casi el 100% del agua.
El valor del ángulo de potencia en estado estacionario es 1,228 rad eléctrico, o 70,36 grados eléctricos. Como este valor es menor a 90 grados eléctricos, según criterio establecido en (Fitzgerald 1996), se afirma que el generador eléctrico opera de forma estable. Si requerimientos impuestos por la curva de capacidad del generador dictan que este debe operar con un ángulo de potencia máximo de 60 grados eléctricos, una vía para reducir el valor de este ángulo a 60 grados eléctricos en estado estacionario sin modificar la potencia suministrada por la turbina y por tanto la potencia eléctrica suministrada a la red, es aumentar la excitación de modo que E l incremente su valor a 244,85 V, como puede verificarse de la ecuación 20.
Conclusiones
En esta primera aproximación se obtuvo el diagrama funcional de centrales maremotérmicas de ciclo abierto o de Anderson emplazadas en tierra y conectadas al SEN. A partir de este se determinó el modelo matemático de cada componente y luego se obtuvo el modelo matemático de dichas centrales maremotérmicas en MatLab/Simulink(. Este modelo de centrales maremotérmicas dota al diseñador de un esquema de simulación en MatLab/Simulink( flexiblemente configurable para enfrentar casos de estudios, y para el escenario analizado dicho modelo arrojó que el porciento de potencia que el sistema aporta al SEN es del 83% de la potencia total producida por el generador eléctrico.