TRABAJOS ORIGINALES

 

Teoría de colas aplicada al estudio del sistema de servicio de una farmacia

 

Queueing theory applied to the study of the service system of a pharmacy

 

 

M.Sc. Ing. Eduardo López Hung^I
 M.Sc. Lic. Lai Gen Joa Triay^II

 

^I Universidad de Ciencias Médicas de Santiago de Cuba. Profesor de Informática y Matemática Aplicada. Profesor Asistente. Investigador Agregado. E-mail: [e-mail]
^II Universidad de Oriente. Profesora Adjunta de Administración de Empresas e Investigación de Operaciones. Profesora Asistente. E-mail:  [e-mail]

 

 

---

RESUMEN

Con frecuencia las instituciones que brindan servicios deben tomar decisiones respecto al caudal de clientes que reciben, así como la capacidad de servicio con que cuentan. Sin embargo, a diario se presenta un fenómeno común y cotidiano: las colas o líneas de espera, las que se generan cuando la demanda excede a la oferta. En este contexto aparece la teoría de colas, la cual no resuelve el problema, pero ofrece información para tomar decisiones, sobre la base de la predicción de algunas características sobre la cola y el sistema de servicio. Un escenario evidente en el sector salud, donde se generan constantemente líneas de espera son las farmacias. En la Farmacia Hospitalaria Principal de Santiago de Cuba, se modeló la venta de medicamentos desde este enfoque, al no contar con otras herramientas que con su aplicación apoyaran la toma de decisiones. Por ello el objetivo del trabajo es determinar desde el enfoque de la teoría de colas, las variables y medidas de rendimiento del sistema de servicio de dicha Farmacia, para la toma de decisiones a corto y mediano plazo, en función de ofrecer un mayor y mejor servicio. Como resultado se determinó que, para el sistema de servicio actual, existe una alta probabilidad de que se generen colas, y que los clientes permanezcan en ella por más de 5 minutos; recomendando garantizar la disponibilidad de los dependientes, reducir el número de clientes en la cola, hacer más amena la estancia en ella, así como valorar y evaluar su rediseño.

Palabras claves: servicios farmacéuticos, sistema de servicios, sistema de colas, líneas de espera, teoría de colas, investigación de operaciones.

---

ABSTRACT

Often the institutions that provide services must make decisions regarding the number of clients they receive, as well as the service capacity they have. However, there is a daily and everyday phenomenon: queues or waiting lines, which are generated when demand exceeds supply. In this context, queueing theory appears, which does not solve the problem, but provides information needed to make decisions, based on the prediction of some characteristics about the queue and the service system. A clear context in the health branch, where there are constantly waiting lines are pharmacies. In the Municipal Community Pharmacy of Santiago de Cuba, the sale of medicinal products was modeled from this approach, since there are no other applied tools that support decision making. Therefore, the objective of the work is to determine from the approach of queueing theory, the variables and measures of performance of the service system of the said Pharmacy, for the decision making in the short and medium term, in function of offering a greater and better service. As a result, it was determined that, for the current service system, there is a high probability that queues will be generated, and that customers will stay in it for more than 5 minutes; recommending to guarantee the availability of dependents, reduce the number of clients in the queue, make the stay in it more enjoyable, as well as assess and evaluate its redesign.

Key words: pharmaceutical services, service systems, queueing systems, waiting lines, queueing theory, operations research.

---

 

 

INTRODUCCIÓN

Se podría aseverar con toda certeza que cualquier persona alguna vez ha formado parte de una cola o línea de espera, con la finalidad de recibir un bien o servicio.

Las colas o líneas de espera se presentan, cuando los clientes o usuarios llegan a un lugar demandando un servicio. Si la persona que ofrece el servicio no está disponible inmediatamente y el cliente decide esperar, entonces se forma una línea de espera.¹ Estas son frecuentes en la vida cotidiana, por ejemplo: para cobrar un salario o estipendio, para abordar algún medio de transporte, para entrar a algún lugar, o para comprar algún producto. Sin embargo, resulta inusitado el hecho de que algo tan común e inadvertido como son las colas, haya sido –y lo sigue siendo– objeto de estudio de las ciencias, y específicamente de una de las técnicas analíticas modernas de la investigación de operaciones: la Teoría de Colas.

La Teoría de Colas surgió a principios del siglo XX, cuando el problema de la congestión de tráfico que se presentaban en las redes telefónicas fue estudiado por primera vez desde un enfoque científico por el danés Agner Kraup Erlang. A partir de ese entonces esta teoría se ha aplicado a multitud de problemas de la vida real, como los mencionados anteriormente.^{2, 3}

El estudio de las colas es importante ya que proporciona tanto una base teórica del tipo de servicio que se puede esperar de un determinado recurso, como la forma en la cual puede ser diseñado. La teoría de colas es una colección de modelos matemáticos que describen sistemas de línea de espera. Dichos modelos sirven para encontrar un balance entre el costo del servicio y el costo asociado a la espera por ese servicio.⁴

Es válido aclarar que no concierne a esta teoría alcanzar la meta de la investigación de operaciones: la toma de decisiones óptimas. En lugar de ello brinda información sobre el comportamiento del sistema de colas, para mejorarlo en función de la satisfacción de los clientes o usuarios, y del desempeño de quienes ofrecen el servicio.⁴

Específicamente en Salud Pública, disímiles son los escenarios en los que se presentan a diario sistemas de servicios, y en los que se generan líneas de espera o colas, por ejemplo, la cola que se genera en una farmacia. No en pocos casos se ha evidenciado el alto índice de descontento de los clientes debido a la larga espera, el escaso número de personal para atender al público, o la demora de quienes ofrecen el servicio, independientemente de que existan otras razones aparentemente sin importancia para esta teoría.

En la Farmacia Hospitalaria Principal de Santiago de Cuba, existe un sistema de servicios para la venta de medicamentos que no en muy pocas ocasiones colapsa, al punto que los usuarios tienen que esperar largos períodos de tiempo en la cola, y en el peor de los casos abandonan la instalación sin adquirir el medicamento necesitado, produciendo insatisfacción. Esta situación pudiera estar condicionada por diversas causas, entre las que se destaca el hecho de ser una de las farmacias más concurridas de la ciudad, el hecho de estar al lado de uno de los hospitales más grandes de la ciudad, el escaso número de dependientes, el excesivo tiempo para atender a los clientes, entre otras. Por ello se hace necesario estudiar dicho sistema de servicio, y determinar de qué forma podría ser mejorado.

Luego el objetivo de este trabajo es: determinar e interpretar las variables y medidas de rendimiento del sistema de servicio de la Farmacia Hospitalaria Principal de Santiago de Cuba, para la toma de decisiones a corto y mediano plazo, en función de ofrecer un mayor y mejor servicio.

 

METODOLOGÍA

Para tener una primera aproximación al sistema de servicio bajo estudio, se tuvieron en cuenta las normas y procedimientos que regulan el desarrollo de las actividades diarias en cualquier farmacia del país.⁵

Se realizaron numerosas observaciones sistemáticas en dicha farmacia en el período comprendido entre septiembre de 2016 y febrero de 2017. Esta cuenta normalmente con dos dependientes para la venta de medicamentos, y se determinó que los clientes llegan como promedio a razón de 110 clientes por hora; y son atendidos como promedio a razón de 65 por hora.

Considerando todos estos elementos, se necesitó realizar un análisis que permita determinar:

·         La probabilidad de que exista una línea de espera.

·         La probabilidad de que no se genere una línea de espera.

·         La probabilidad de que un cliente permanezca en cola por más de 5 minutos.

·         Medidas de rendimiento del sistema en estado estacionario.

Se propuso utilizar la Teoría de Colas como herramienta para cumplimentar el objetivo de la investigación. Para describir el sistema de servicio a modelar, se utilizó la notación extendida de Kendall, a través de la cual se especifica: la distribución de probabilidad de los tiempos entre llegadas, la distribución de probabilidad de los tiempos de servicio, cantidad de servidores, cantidad máxima de usuarios simultáneos que se admiten en el sistema, y disciplina de la cola, respectivamente.^{4, 7}

En este caso el sistema de servicio bajo estudio se modeló como un sistema de colas del tipo: M/M/C, debido a:

·         El proceso de llegadas es un proceso markoviano de tipo Poisson–exponencial –de ahí la primera M–, es decir que las llegadas siguen una distribución de Poisson, y la duración de los intervalos entre las mismas tiene una distribución exponencial .^{6, 8, 9} En el caso estudiado las llegadas al sistema son aleatorias, con tasa media fija, y el tamaño de la fuente de entrada es infinito.

·         La segunda M designa el proceso de servicio, y describe la distribución del tiempo de servicio y, por tanto, de las salidas del sistema. Esta distribución es independiente a la distribución del tiempo entre llegadas consecutivas, pero del mismo tip^{6, 8, 9} –de ahí la segunda M–.

·         La C designa la cantidad de servidores o canales de servicio, e indica que pueden haber más de un servidor o canal de servicio.

Es importante destacar otros elementos de este modelo de cola, y que, por constituir valores por defecto, la propia notación hace que se omitan:

·         El número máximo de usuarios simultáneos que se admiten en el sistema es infinito. Este es el valor tomado por defecto para este elemento, y por ello se omitió en la notación.

·         La disciplina de la cola que se establece es que primero se le da servicio al primero que ha llegado, de forma que la cola está ordenada según el orden de llegada de los usuarios, y se especifica con las siglas FIFO (del inglés First–In, First–Out). Este es el valor tomado por defecto para este elemento, y por ello se omitió en la notación.

Teniendo en cuenta estos elementos, se definieron los siguientes parámetros:

·          (tasa de llegadas, parámetro de Poisson, o número medio de llegadas por unidad de tiempo). En este caso  clientes por hora.

·          (tasa de servicio, o número medio de clientes servidos por unidad de tiempo). En este caso  clientes por hora.

·         (cantidad de servidores o canales de servicio). En este caso .

·         El sistema es estacionario, lo cual se puede afirmar al comprobar que , es decir, que la intensidad de tráfico por canal es inferior al número de canales. Esta condición es necesaria y suficiente en este modelo para demostrar que el sistema es estacionario; estado que garantiza que la probabilidad de que haya un determinado número de usuarios en el sistema sea igual en cualquier instante.^{4, 6, 8, 9}

 

RESUTADOS Y DISCUSIÓN

Probabilidad de que exista una línea de espera

La probabilidad de que exista una línea de espera, implica que haya en el sistema como mínimo tres clientes, es decir dos recibiendo servicio –es preciso recordar que se cuenta sólo con dos dependientes–, y como mínimo un cliente en la línea de espera, es decir que debe haber más de dos clientes en la farmacia simultáneamente. Esta probabilidad se calculó excluyendo la probabilidad de que no haya clientes, o haya uno o dos; tal y como se muestra en la siguiente ecuación:

donde  es la probabilidad de que haya  clientes en el sistema, y que se determina a través de la siguiente fórmula ^{(4, 8, 9)}:

Se obtuvo la probabilidad para  indistintamente, y así calcular la probabilidad de que haya más de dos clientes simultáneamente en la farmacia.

La probabilidad de que en el sistema no haya clientes () fue:

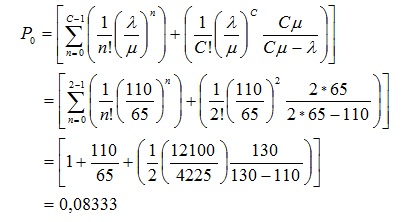
La probabilidad de que en el sistema exista un solo cliente () fue:

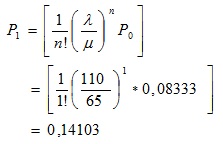
La probabilidad de que en el sistema existan solo dos clientes () fue:

Luego,

 

Interpretación:

Esto significa que existe una probabilidad considerable (aproximadamente un 66%) de que en el sistema siempre haya una cola o línea de espera, aún cuando ambos dependientes estén disponibles para prestar el servicio.

Probabilidad de que no se genere una línea de espera

La probabilidad de que no se genere una cola o línea de espera a la llegada de un nuevo cliente, se produce cuando obviamente no existen clientes en línea de espera, y al menos uno de los dependientes esté ocioso o inactivo por no haber clientes que atender. Para esta última condición deberían existir en el sistema como máximo un solo cliente, por lo que esta probabilidad se obtuvo a través de la ecuación:

Luego, teniendo en cuenta los valores hallados anteriormente,

Interpretación:

Esto indica que existe una probabilidad relativamente baja (aproximadamente un 22%) de que algún dependiente esté ocioso o inactivo, es decir, que es poco probable que no se genere alguna línea de espera a la llegada a la farmacia de un nuevo cliente.

Probabilidad de que un cliente permanezca en cola por más de 5 minutos

Para el cálculo de esta probabilidad, se debe tener en cuenta la función de distribución del tiempo de espera en la cola ,^{4, 8, 9} como se muestra a continuación:

donde las tasas de llegadas y de servicio deberán se expresaron en minutos:

 clientes por minuto.

 clientes por minuto.

Por tanto, la probabilidad de que un cliente permanezca por más de 5 minutos () en la cola se obtuvo a partir de la siguiente ecuación:

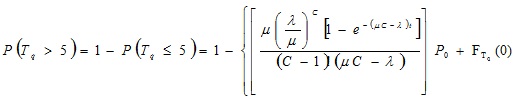
Para ello primeramente se obtuvo el valor de  a través de la ecuación:

 

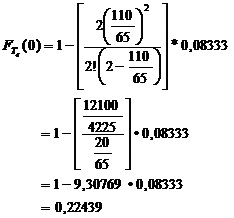
Con el valor hallado anteriormente, y habiendo calculado previamente el valor de , se obtuvo la probabilidad en cuestión, obteniendo:

Interpretación:

Esto indica que un cliente tiene una probabilidad considerable (aproximadamente de un 60%) de permanecer en la cola por más de 5 minutos.

Medidas de rendimiento del sistema en estado estacionario

Las medidas de rendimiento del sistema en estado estacionario constituyen una valiosa información sobre el sistema de servicio que se estudia, en tanto muestran por una parte el número de clientes promedio en el sistema, bien sea en espera del servicio o recibiéndolo; y por otra el tiempo promedio que estarán los clientes en la cola o en el sistema de manera general.⁴

Primeramente, se obtuvieron las medidas relativas al número medio de usuarios, y al tiempo medio en que estos están en la cola. En cuanto al número medio de usuarios en la cola, se obtuvo a través de la ecuación:

 

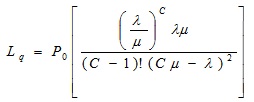
obteniendo que:

A partir de esta fórmula, y teniendo en cuenta las fórmulas de Little, se obtuvo el tiempo medio que un usuario pasa en la cola, a través de la ecuación:

obteniendo que:

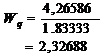
Ya con las dos medidas anteriores, se calcularon las mismas medidas de rendimiento, pero para el sistema. Se obtuvo el tiempo medio que un usuario pasa en el sistema, a través de la ecuación:

 

obteniendo que:

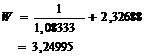
Con el valor anterior, se obtuvo el número medio de usuarios en el sistema:

obteniendo que:

Interpretación

Como promedio habrá en la línea de espera 4 clientes, y permanecerán en ella poco más de 2 minutos. En el caso del sistema de servicio bajo estudio, como promedio en cada minuto habrá aproximadamente 6 clientes, permaneciendo en el mismo poco más de 3 minutos.

Tomando en consideración los resultados obtenidos anteriormente, y en función de la toma de decisiones a corto y mediano plazo, se sugirió a la administración de la farmacia de referencia:

·         Garantizar siempre la disponibilidad de ambos dependientes para brindar el servicio con la calidad requerida, ya que existe una alta probabilidad de que siempre haya una cola.

·         Buscar alternativas para reducir el número de clientes en la cola cuando esta última experimenta por momentos un crecimiento considerable.

·         Buscar alternativas que hagan más amena la estancia en la cola, y en el sistema de manera general, ya que los clientes tienen una alta probabilidad de permanecer en la cola por más de 5 minutos.

·         Valorar el rediseño del sistema de servicio modificando su capacidad, evaluarlo a través de herramientas matemático–computacionales, y compararlas con el sistema de servicio implantado actualmente.

Constituye este un primer acercamiento al estudio del sistema de servicios que se establece en una farmacia, del que los autores no encontraron referencias de su realización en contextos similares. Dicho análisis permitió la utilización de instrumentos de la investigación de operaciones en uno de los problemas de toma de decisiones que ya se convierte en cotidiano, y que algunas veces mella el prestigio y la confianza de los clientes en las instituciones de servicios, como es el caso de la farmacia de referencia.

 

CONCLUSIONES

La mayoría de las técnicas de análisis de la investigación de operaciones tienen como objetivo principal optimizar. Sin embargo, existen algunas técnicas en esta rama como es el caso de la teoría de colas, cuyo objetivo no es la optimización. Esta teoría –por demás con un sólido basamento en la teoría de las probabilidades–, busca estudiar cómo se comporta un sistema de cola bajo ciertos parámetros, en función de la toma de decisiones.

Muchos son los contextos donde esta es aplicable, ejemplificado en este trabajo a través de un problema práctico, en este caso el sistema de servicio establecido en la Farmacia Hospitalaria Principal de Santiago de Cuba. Dicho problema se modeló a través de un sistema de servicio con llegadas de tipo Poisson – exponencial, con dos servidores, y con una disciplina FIFO; con el fin de estudiarla, y desde esta perspectiva determinar, aquellos parámetros que permitieran valorar el rendimiento del sistema de servicio actualmente en explotación, y en consecuencia la toma de decisiones a corto y mediano plazo, en función de ofrecer un mayor y mejor servicio.

Se pudo determinar a través de los parámetros calculados que, el diseño del sistema de servicio en dicha farmacia muestra que existe una alta probabilidad de que se generen colas, y que los clientes permanezcan en ella por más de 5 minutos. Por ello las recomendaciones para la toma de decisiones fueron encaminadas a garantizar la disponibilidad de los dependientes, trazar estrategias que coadyuven a reducir el número de clientes en la cola, hacer más amena la estancia en ella, así como valorar y evaluar su rediseño.

 

REFERENCIAS BIBLIOGRÁFICAS

1.      Hillier FS, Lieberman GJ. Fundamentos de Investigación de Operaciones. 9na ed. México D.F.: McGraw–Hill Interamericana; 2014.

2.      Winston WL. Investigación de Operaciones. Aplicaciones y Algoritmos. 4ta ed. Stamford: Editorial Thomson Internacional; 2004.

3.      Chase RB, Jacobs FR, Aquilano RJ. Administración de Operaciones. 12ma ed. México D.F.: McGraw–Hill Interamericana; 2009.

4.      Shortle JF, Thompson JM, Gross D, Harris CM. Fundamentals of Queueing Theory. 5th Edition. New York: John Wiley & Sons, Inc.; 2017.

5.      Manual de Normas y Procedimientos en una Farmacia Comunitaria. Ministerio de Salud Pública. (junio de 2005).

6.      Medhi J. Stochastic Models in Queueing Theory. 2nd Edition. New York: Academic Press; 2002.

7.      Haghighi AM, Mishev DP. Delayed and Network Queues. New York:  John Wiley & Sons, Inc.; 2016.

8.      Allen A. Probability, Statistics, and Queueing Theory. 2nd Edition. New York: Academic Press; 2014.

9.      Asmussen S. Applied Probability and Queues. New York: Springer–Verlag; 2003.

 

 

Recibido: 14 de enero de 2018.

Aprobado: 12 de marzo de 2018.