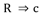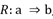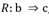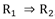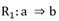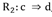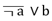Artículo original

¿Por qué emplear el análisis estadístico implicativo en los estudios de causalidad en salud?

Why Use the Implicative Statistical Analysis in Studies of Health Causality?

Dra. Nelsa María Sagaró del Campo^{1  *}  , Dra. C. Larisa Zamora Matamoros² 

¹ Universidad de Ciencias Médicas. Santiago de Cuba, Cuba.

² Universidad de Oriente. Santiago de Cuba, Cuba.

RESUMEN

El análisis estadístico implicativo es una técnica de minería de datos, surgida para resolver problemas de la didáctica de las matemáticas, se basa en la inteligencia artificial y el álgebra booleana, para modelar la casi implicación entre eventos y variables de un conjunto de datos. El objetivo de este ensayo es exponer las evidencias teóricas y prácticas que demuestran su utilidad para el estudio de la causalidad en la salud, para lo cual se realizó una revisión exhaustiva del tema en las bases de datos bibliográficas alojadas en Internet. Se presentan una serie de razones que justifican el uso de esta técnica en estudios de causalidad en medicina, en relación con el número de variables, el tamaño de la muestra, los supuestos requeridos para su aplicación y la naturaleza asimétrica de sus índices. También se identifican algunas ventajas con respecto a las técnicas estadísticas tradicionales, como la detección de eventos raros, que pasan inadvertidos a medidas como el apoyo y la confianza. Finalmente, se mencionan las investigaciones clínico-epidemiológicas donde se ha utilizado este análisis.

Palabras-clave: Análisis estadístico implicativo; cuasi-implicación; similaridad; cohesión; entropía; causalidad en medicina; técnicas estadísticas

ABSTRACT

Implicative statistical analysis is a technique of data mining, emerged to solve problems of the Didactic of mathematics, it is based on Artificial Intelligence and Boolean Algebra, to model the quasi-implication between events and variables of a data set. The objective of this essay is to expose the theoretical and practical evidences that demonstrate its utility for the study of causality in health, for which an exhaustive review of the subject was carried out in the bibliographic databases hosted on the internet. A series of reasons are presented that justify the use of this technique in causality studies in medicine, regarding the number of variables, the sample size, the assumptions required for its application and the asymmetric nature of its indices. Also some advantages are identified with respect to traditional statistical techniques such as detection of rare events, which would go unnoticed to measures such as support and trust. Finally, clinical-epidemiological investigations where this analysis has been used are mentioned.

Key words: Implicative statistical analysis; quasi-implication; similarity; cohesion; entropy; causality in medicine; statistical techniques

Introducción

La sociedad actual genera datos de manera exponencial y se requiere de herramientas, procedimientos y nuevos métodos de análisis que permitan extraer el conocimiento subyacente a dichos datos y ajustarlos a modelos comprensibles por el ser humano, que permitan predecir información futura.¹El desarrollo apreciable de las matemáticas, de las técnicas informáticas y de las ciencias básicas, permiten plantear modelos matemáticos cada vez más cercanos al comportamiento real del proceso salud-enfermedad.²

Un ejemplo de ese desarrollo es el análisis estadístico implicativo, conocido por la sigla ASI de Analyse Statistique Implicative del idioma francés donde se originó, es una herramienta de la minería de datos basada en las técnicas estadísticas multivariadas, la teoría de la cuasi-implicación, la inteligencia artificial y el álgebra booleana, para modelar la cuasi-implicación entre los sucesos y variables de un conjunto de datos. ³

Esta técnica surgió para solucionar problemas de la Didáctica de la matemática y fue creada por el francés Régis Gras,^4-6 profesor emérito de la Universidad de Nantes, Francia, quien comenzó sus trabajos en este campo en 1980, y desde entonces ha venido estudiando el fenómeno de la creación de reglas inductivas no simétricas y de la cuantificación de la probabilidad de que se presente una cierta característica b si se ha observado otra característica a en la población. El ASI contempla la estructuración de datos, interrelacionando sujetos y variables, la extracción de reglas inductivas entre las variables y, a partir de la contingencia de estas reglas, la explicación y en consecuencia una determinada previsión en distintos campos del saber.⁷

El objetivo de este trabajo es identificar los aspectos teóricos y prácticos que justifican el empleo de esta técnica en los estudios de causalidad en medicina para lo cual se llevó a cabo una exhaustiva revisión de la literatura sobre el tema en las bases de datos bibliográficas alojadas en la Internet para sintetizar y sistematizar la bibliografía encontrada.

Implicación y cuasi-implicación como antecedentes del ASI

Los hechos y fenómenos de la realidad están concatenados por las llamadas relaciones causales. Estas relaciones causales son captadas por el pensamiento humano de acuerdo a los hechos pasados y las expectativas, son expresadas en el lenguaje mediante las oraciones condicionales y formalizadas según la Lógica mediante expresiones llamadas implicaciones. Una implicación es una afirmación que conlleva a otra afirmación relacionando una causa (A) con un efecto (B), y se escribe, formalmente, según la lógica proposicional como A ⇒ B, donde A es una causa o conjunto de causas y B el efecto o conjunto de efectos esperados de esa causa.⁸

La implicación A ⇒ B puede ser expresada como “si A entonces B” y si esa proposición es verdadera se dice que “A es condición suficiente para B”, por el contrario, si la implicación B ⇒ A es verdadera, “A es condición necesaria para B”. Cuando se satisface la implicación en ambos sentidos (coimplicación), B es verdadera si y sólo si lo es A, caso que se puede denotar como A ⇔ B, y significa que A es condición necesaria y suficiente para B.

En las matemáticas el determinismo es total por lo que toda regla (teorema) no sufre de excepción; en cambio en las situaciones naturales, sociales o de las ciencias biomédicas no existe un determinismo total por lo que los teoremas del tipo “si a entonces b” no pueden establecerse a causa de las excepciones que los niegan. Es por eso que la epidemiología denomina factor de riesgo al factor que aumenta la probabilidad de que ocurra un desenlace y no a la causa de un desenlace. Esa imposibilidad (contradicción) motivó la necesidad de profundizar en los datos para encontrar reglas fiables del tipo teoremas parciales surgiendo así la teoría de la cuasi-implicación o implicación estadística a partir de la dialéctica “ejemplos-contraejemplos”.¹

En la teoría cuasi implicativa las reglas del tipo “si a entonces b” son aceptables y aplicables, mientras que el número de contraejemplos sea "admisible“, por ejemplo, se sabe que el hábito de fumar constituye un factor de riesgo para el cáncer de pulmón pero no se puede esperar de manera absoluta que “si fuma entonces padecerá cáncer de pulmón” pero, el hecho de que algunos pacientes fumadores no desarrollen el cáncer de pulmón (contraejemplo) no invalida el hecho de que el tabaquismo sea un factor de riesgo para desarrollar dicha enfermedad.

El concepto de cuasi-implicación relaja al de implicación, de modo que se trata de una regla que admite contraejemplos: "cuando un individuo presenta el rasgo a, entonces, generalmente, también presenta el rasgo b". La validez de la regla depende entonces de la probabilidad o fuerza de la cuasi-implicación, la cual se determina al comparar el número de contraejemplos presentes, con los que aparecerían bajo una ausencia de relación estadística.

Como se plantea en Gras,^1,9 el estudio de este concepto de cuasi-implicación como objeto matemático, en los campos de las Probabilidades y de la Estadística, permitió construir las herramientas teóricas en que se fundamenta el ASI, que permiten identificar una posible relación causal y formular hipótesis con fines descriptivos y, si es posible, predictivos.

Principales categorías del ASI

En el ASI la validez de la regla a ⇒b depende de la probabilidad o fuerza de la cuasi-implicación, que se determina al comparar el número de contraejemplos presentes que invalidan dicha regla con los que aparecerían bajo una ausencia de relación estadística.

El ASI consta de tres procedimientos:

1. La implicación, donde se destacan tres conceptos básicos:

   • La intensidad implicativa: medida probabilística de la validez de la regla. La decisión de aceptar o no la regla está en función del nivel de significación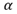elegido por el investigador y se dirá que la regla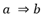es admisible para un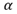dado si la cantidad de contraejemplos esperados es menor que los observados.

   • El índice de implicación: indicador de la no implicación de a sobre b. Este índice es no simétrico y no coincide con el coeficiente de correlación u otros índices simétricos que miden asociación.

   • El índice de implicación-inclusión o de implicación entrópica: versión entrópica del índice de implicación que supera la poca discriminación de este en muestras grandes. Este índice permite determinar el criterio entrópico al integrar la información a partir de la presencia de un escaso número de contraejemplos, tanto por la reglacomo por su negación

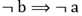
2. La cohesión, que permite estructurar el conocimiento en forma de reglas y meta reglas y superar la simple articulación de las partes de una tipología clásica, a fin de alcanzar un todo significativo al ser de carácter no lineal, asimétrico, jerárquico y dinámico. Las reglas y meta reglas que surgen se pueden presentar en tres esquemas:

   • , donde , que se interpreta como que c es consecuencia de la regla R.

   • , donde , que se interpreta como que a se dedujo de la regla R o que la regla R es consecuencia de a.

   • , donde y , que se interpreta como que se dedujo de la reglao que la regla es consecuencia de.

   • Intuitivamente, la cohesión mide el desequilibrio de las frecuencias de los eventos y a favor del primero.

3. La similaridad como medida de correspondencia o semejanza entre los objetos que van a ser agrupados. A diferencia de los métodos de clasificación usualmente empleados, en el ASI se emplea el índice de similaridad de Lerman, que es la probabilidad de que el número observado de copresencias entre dos variables sea mayor o igual que el de las copresencias esperadas por el azar.

Además de los procedimientos antes descritos, el ASI permite cuantificar el aporte de cada individuo en la formación de las estructuras que se obtienen a partir de los índices de cohesión y de similaridad, para lo cual emplea la contribución o la tipicalidad de cada sujeto. La tipicalidad es un índice porcentual que mide cómo se comporta un individuo en relación a la regla o a la clase, llamando sujeto típico a aquél que verifica todas las implicaciones (similaridades) que poseen mayor intensidad de implicación (índice de similaridad) en la formación de las reglas (clases). La contribución cuantifica el aporte de un determinado individuo en la formación de la regla o de la clase.

Razones que hacen posible el empleo del ASI en el estudio de la causalidad en salud

Hechos concretos hacen posible la utilización de esta técnica en la identificación de factores pronósticos o de riesgo. Entre ellos estas autoras han identificado los siguientes:

1. Existe la herramienta informática que permite el procesamiento automatizado para la aplicación del ASI: es un software específico designado por el acrónimo CHIC (del francés: Classification Hiérarchique Implicative et Cohésitive que significa Clasificación Jerárquica, Implicativa y Cohesitiva), el cual proporciona de forma rápida, gran cantidad de cálculos y gráficos.^10-12

2. No requiere del cumplimiento de supuestos para que sus resultados sean válidos.

3. Admite el tratamiento de variables medidas en cualquier escala, binarias, modales, frecuenciales, de intervalo y hasta difusas, sin distinción entre variables dependientes e independientes o covariables.

4. No tiene restricción en cuanto al número de variables o requisitos que deben cumplir para entrar o salir del análisis.

5. Las variables pueden ser analizadas como variables principales o suplementarias, tanto en el análisis cohesitivo como en el de similaridad.La variable suplementaria es extrínseca al estudio, no interviene directamente en las relaciones entre las variables principales, pero permite esclarecer la importancia o la superfluidad de estas categorías en la formación de las reglas o meta reglas. Generalmente se emplean variables modales como variables suplementarias. Esta posibilidad puede ser aprovechada en los estudios de causalidad en biomedicina para determinar cuánto contribuyen los casos o los controles a la formación de las relaciones entre las variables, empleando las variables que representan el desenlace como suplementarias.

6. No hay criterios restrictivos en cuanto al tamaño de muestra para la aplicación. Se puede trabajar con muestras pequeñas o extremadamente grandes. En dependencia del tamaño de muestra se seleccionará una distribución u otra a la hora de estimar los índices en el análisis. La distribución que siguen estas variables aleatorias depende del patrón asumido para seleccionar los subconjuntos, pudiendo ser la hipergeométrica (cuando la población es finita y la muestra es de tamaño fijo), binomial (población infinita y tamaño de muestra fijo) o Poisson (población infinita y tamaño de muestra aleatorio). Bodín¹³ detalla los modelos y pruebas de hipótesis para cada distribución. El trabajo con muestras grandes requiere que el investigador elija el enfoque entrópico a la hora de llevar a cabo el análisis implicativo. El cálculo del tamaño de muestra dependería del diseño empleado en el estudio, generalmente caso y control o cohorte.^14,15

7. Permite estimar la relación existente entre una variable dependiente y una o más variables independientes, así como la relación entre las propias variables independientes, es decir, muestra todas las relaciones entre las variables con diferentes intensidades de implicación. A medida que el investigador selecciona una intensidad de implicación menor aparecen nuevas variables y nuevas relaciones entre ellas.

8. Permite el trabajo con cuatro niveles de intensidad implicativa a la vez, que se modifican según el criterio del investigador y que permiten un análisis más amplio y una interpretación más completa del fenómeno de la causalidad. A medida que el investigador decide disminuir este nivel pueden aparecer nuevas relaciones y/o nuevas variables se incluyen en la trama causal.

9. Por restringirse a sucesos frecuentes desoye lo trivial, por lo que no se afectan sus resultados frente a observaciones raras o atípicas.

10. Aporta información diferente al resto de los análisis estadísticos mediante sus tres índices básicos: de similaridad, de cohesión y de implicación. Además muestra indicadores como: la frecuencia absoluta de ocurrencia de cada variable, su media y desviación estándar, la frecuencia de ocurrencia de cada pareja de variables que se pueden formar y sus coeficientes de correlación.

11. Los resultados se presentan en tres gráficos que facilitan la interpretación de los mismos: arboles de similaridad, de cohesión y el grafo implicativo que puede ser general y también en modo cono según decida el investigador. Estas autoras consideran apropiado formar dos grafos en modo cono para la identificación de factores de riesgo o pronóstico ubicando en cada cono el peor y mejor desenlace. También se muestran múltiples cuadros donde constan las frecuencias absolutas de ocurrencia de cada variable, sus medias y desviaciones estándares, las frecuencias de ocurrencias de cada par de variables que se pueden formar, así como sus coeficientes de correlación, los índices de similaridad, de cohesión implicativa y de implicación inclusión, las tipicalidades y contribuciones de los individuos.

12. Es muy atractivo al brindar índices y gráficas, creados automáticamente, donde es fácil apreciar las relaciones entre todo el conjunto de variables. Los grafos implicativos generados son similares a los diagramas causales (grafos acíclicos dirigidos o DAG de sus siglas en inglés Directed Acyclic Graphs) que permiten plantear posibles rutas de asociación entre causas y efectos, así como otras rutas alternativas que pueden ocasionar sesgos por lo que facilitan también el control de posibles sesgos.^16-19) Los DAG permiten identificar los factores que influyen sobre un desenlace pero no permiten identificar si influyen a favor o en contra de este. Sin embargo, estas autoras consideran que mediante el grafo implicativo en modo cono del ASI se puede reconocer cuando un factor es protector o de riesgo.

13. Puede servir como método gráfico para el análisis exploratorio de datos, por ejemplo, para decidir entre las variables a incluir en un modelo de regresión.

14. Este análisis no se contradice con el análisis actual, sino que lo complementa y enriquece desde una perspectiva diferente. El mismo está acorde con el paradigma de la complejidad que se propone actualmente, ya que cumple con sus principios tales como: el principio dialógico al asociar nociones contradictorias que forman parte del mismo fenómeno como los ejemplos y contraejemplos, el principio hologramático al suponer las partes en el todo y el todo en las partes y ver el todo como algo complejo, no como la simple suma de sus partes y el principio de la recursividad que rompe con la relación lineal entre causa y efecto. Por tanto resulta atrayente su empleo, teniendo en cuenta que los fenómenos biomédicos pueden ser complejos, abiertos, dinámicos, sensibles a pequeñas variaciones de sus condiciones iniciales, de sus fluctuaciones internas y/ o fluctuaciones externas que los desestabilizan.^2,20

Ventajas del ASI con respecto a las técnicas estadísticas tradicionales

Algunas diferencias del ASI con las técnicas estadísticas tradicionales constituyen ventajas que justifican su empleo y reafirman su utilidad, por ejemplo:

• Las técnicas tradicionales de asociación, como las pruebas de independencia y homogeneidad de chi cuadrado, dadas dos variables A y B, se basan en la estimación de la frecuencia de ocurrencia de “A y B” y de “no A y no B”, sin embargo, no tienen en cuenta la rareza de ocurrencia de “A y no B”, lo cual las invalidan para descubrir sucesos raros.³ El ASI encuentra sucesos raros, que pasan inadvertidos a medidas como el soporte y la confianza.

• Los coeficientes de correlación paramétricos y no paramétricos están basados en medidas lineales y simétricas. Las demás técnicas multivariadas de análisis de conglomerados, análisis factorial y análisis de correspondencias están basadas en matrices de covarianzas o de correlaciones, o las nociones simétricas de similaridad y distancia. En el ASI todos los índices son asimétricos, no lineales, en correspondencia con la complejidad de los procesos naturales como la salud-enfermedad.

• El análisis de senderos, el modelo multivariado más empleado en las ciencias sociales para probar conjuntos de supuestos causales entre variables, solo tiene en cuenta las relaciones entre variables de tipo lineal o aditiva y excluye las relaciones curvilíneas y multiplicativas (de interacción). Además requiere como supuestos la homocedasticidad de varianzas y baja multicolinealidad.²¹Estos requerimientos son superados en el ASI.

• La regresión logística binaria, la más popular y empleada de las técnicas estadísticas para el estudio de la causalidad en ciencias médicas, identifica solamente factores con fuerte asociación a un desenlace a partir de un reducido conjunto de posibles factores causales, no permite visualizar las relaciones existentes entre el conjunto completo de variables estudiadas, ya que al considerar la no existencia de multicolinealidad como supuesto básico conlleva a excluir del modelo las covariables correlacionadas. Algunos autores como Silva²² coinciden que el modelo logístico requiere de la existencia de una relación lineal entre el logit de la probabilidad del suceso de interés y las variables independientes, que algunas observaciones “raras” pudieran tener una influencia exagerada en las estimaciones de los parámetros del modelo o que otra función distinta de la logística fuese mejor para describir las observaciones a pesar de un buen ajuste del modelo a los datos. Dunkler²³ plantea que el procedimiento paso a paso hacia detrás puede excluir confusores del modelo o dejar falsos confusores, dado que la selección se realiza a través de algoritmos basados en el valor p (índice decreciente de la fiabilidad de un resultado), sin la opinión del investigador. Además, si se incluyen muchas variables, se requiere un tamaño de muestra grande, de al menos 10 sujetos por cada variable independiente para lograr estimaciones adecuadas. Como se planteó antes, todas estas dificultades son superadas por el ASI.

Investigaciones de causalidad en salud que demuestran la utilidad del ASI

Relativo a la aplicación de esta técnica para estudiar causalidad en el campo de las ciencias médicas, al explorar vía internet, los catálogos de publicaciones, sitios y las bases de datos de carácter biomédico, se encontró el estudio de La Spada²⁴de seguimiento de pacientes positivos al virus de la hepatitis C con transaminasas séricas persistentemente normales y las investigaciones previas de estas autoras conducentes a la formación de especialistas en Bioestadística de las provincias orientales Santiago de Cuba, Guantánamo y Granma. Estos últimos trabajos han validado la efectividad del ASI en la identificación de factores pronósticos o de riesgo utilizando como estándar de oro la regresión logística binaria al ser aplicada en estudios observacionales de tipo casos y controles clásicos o anidados en una cohorte. Para realizar la validación de la capacidad diagnóstica del ASI se han estimado en cada estudio realizado indicadores como: sensibilidad, especificidad, valores predictivos, razones de verosimilitud, índice de validez, odds ratio de diagnóstico, entre otros.^25-29

Los resultados obtenidos de estas investigaciones reafirman la utilidad de esta técnica en el contexto médico.

Consideraciones Finales

En el ASI se establece una cuasi-implicación entre variables, que es una relación asimétrica, donde los conjuntos de reglas obtenidas pueden conducir a hipótesis de causalidad sin restricción con respecto al número de variables y al tamaño de la muestra. Basado en el número de contraejemplos, tiene capacidad predictiva y sus resultados son extrapolables a distintos tamaños de muestras, encuentra sucesos raros, que pasarían desapercibidos a medidas como el soporte y la confianza, por restringirse a sucesos frecuentes y no se afecta por observaciones atípicas, todo lo cual constituye una ventaja inminente sobre las técnicas estadísticas clásicas empleadas para identificar posibles factores causales.

La identificación de las razones anteriores y algunas ventajas del ASI con respecto a las técnicas estadísticas tradicionales, unido a los resultados de los estudios clínico-epidemiológicos para la identificación de factores pronósticos y de riesgo llevados a cabo con el empleo de esta técnica han demostrado su validez y posibilidades de empleo en este campo.

Referencias Bibliográficas

1.  Gras R. L'Implication Statistique. Nouvelle méthode exploratoire de données, La Pensée sauvage, éditions, Francia. 1996.

2.  Betancourt Betancourt JA, Ramis Andalia RM. Apuntes sobre el enfoque de la complejidad y su aplicación en la salud. Rev Cubana Salud Pública. 2010;36(2). Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S0864-34662010000200010&lng=es&nrm=iso&tlng=es2.

3.  Valls Pla X, Gregori Huerta P. Diseño de un paquete R para el Análisis Estadístico Implicativo Trabajo Final de Master en Matemática Computacional. Universitat Jaime I, 2014. Disponible en: repositori.uji.es/xmlui/bitstream/handle/10234/107441/TFM_2013_vallsX.pdf?3.

4.  Gras R, Suzuki E, Guillet F, Spagnolo F. Statistical Implicative Analysis, Theory and Applications Springer, 2008. ISBN: 978-3-540-78982-6

5.  Gras R. Genese et developpement de l’analyse statistique implicative: retrospective Historique. Educ. Matem. Pesq., São Paulo, 2014;16(3):645-661.

6.  Gras R, Régnier JC, Lahanier-Reuter D, Marinica C, Guillet F. L'Analyse Statistique Implicative. Des Sciences dures aux Sciences Humaines et Sociales 3ème édition revue et augmentée. 2017.

7.  Orús P, Zamora L, y Gregori P. Teoría y aplicaciones del Análisis Estadístico Implicativo. Primera aproximación en lengua hispana. Universitat Jaume I, Castellón de la Plana: Innovació Digital Castelló, s.l.u. 2009.

8.  Kenneth HR. Discrete Mathematics and Its Applications. Seventh Edition McGraw-Hill, 2012:1-8.

9.  Gras R, Régnier JC, Guillet F. Analyse Statistique Implicative. Une méthode d'analyse de données pour la recherche de causalités. RNTI-E-16 2009. Disponible en: http://www.cepadues.com/livre_details.asp?l=8979.

10.  Couturier R. CHIC: Cohesive hierarchical implicative classification, Statistical Implicative Analysis, Springer, 2008.Disponible en: http://www.springer.com/us/book/978354078982610.

11.  Gras R, Couturier R, Gregori P. Un mariage arrangé entre l’implication et la confiance? VII International Conference SIA, 2015.

12.  Couturier R, Gregori P. Classification en utilisant les règles d’implication de l’ASI. Conference Paper October 2017. Disponible en: https://www.researchgate.net/publication/32477068212.

13.  Bodin A. Analyse implicative: modèles sous-jacents à l’analyse implicative et outils complémentaires. IRMAR, 1997;(32).

14.  Peralta ML. Estudios para establecer el origen o causalidad. Dermatología Rev Mex 2005;49(6).

15.  Mitchell H, Gail MH, Haneuse S. Power and Sample Size for Multivariate Logistic Modeling of Unmatched Case-Control Studies. Stat Methods Med Res. Author manuscript; Disponible en: PMC 2018 July 01.

16.  Rodrigues Cortes T, Faerstein E, Struchiner CJ. Utilização de diagramas causais em epidemiologia: um exemplo de aplicação em situação de confusão. Cad. Saúde Pública, 2016;32(8):e00103115. Disponible en: http://dx.doi.org/10.1590/0102-311X0010311516.

17.  Brewer L, Wright J, Rice G, Neas L, Teuschler L. Causal inference in cumulative risk assessment: The roles of directed acyclic graphs. Environ Int 2017;102: 30-41.

18.  Greenland S, Pearl J. Causal diagrams. Wiley Stats Ref: Statistics Reference Online,John Wiley & Sons, Ltd. 2017 DOI:10.1002/9781118445112.stat03732.pub2

19.  Werlinger F, Cáceres D. Aplicación de grafos acíclicos dirigidos en la evaluación de un set mínimo de ajuste de confusores: un complemento al modelamiento estadístico en estudios epidemiológicos observacionales. Rev. méd. Chile 2018;146(7):907-913. Disponible en: http://dx.doi.org/10.4067/s0034-98872018000700907 19.

20.  Morin E. La epistemología de la complejidad. Gazeta de Antrpología 2004;20(02) Disponible en: http://hdl.handle.net/10481/725320.

21.  Briones G. Metodología de la investigación cuantitativa en las ciencias sociales. ARFO Editores e Impresores Ltda. Bogotá Colombia, 2002.

22.  Silva Ayçaguer LC, Barroso Ultra IM. Regresión logística. Madrid: La muralla, 2000.

23.  Dunkler D, Plischke M, Leffondré K, Heinze G. Augmented backward elimination: pragmatic and purposeful way to develop statistical models. Plos One [internet] 2014;9(11):e113677. Disponible en: http://journals.plos.org/plosone/article?id=10.1371/journal.pone.011367723.

24.  La Spada E, Soresi M, Giannitrapani L, Montalto G, Spagnolo F. Hepatitis C Virus-positive patients with persistently normal serum transaminase: a long-term follow-up. Quaderni di Ricerca in Didattica (Mathematics) 2010;(20)Supplemento n.1.

25.  García Mederos Y, Zamora Matamoros L, Sagaró del Campo N. Análisis estadístico implicativo en la identificación de factores de riesgo en pacientes con cáncer de pulmón. MEDISAN. 2015;19(8). [citado 10 Ene 2018]; Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1029-30192015000800003 25.

26.  Moraga Rodríguez A, Zamora Matamoros L, Sagaró del Campo NM, Moraga Rodríguez A, Rodríguez Griñán A. Análisis estadístico implicativo para la identificación de factores pronósticos de la mortalidad por cáncer de pulmón. MEDISAN. 2016;20(3). [citado 10 Ene 2018]; Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1029-30192016000300010 26.

27.  Moraga Rodríguez A, Zamora Matamoros L, Sagaró del Campo NM, Moraga Rodríguez A, Rodríguez Griñán A. Análisis estadístico implicativo para la identificación de factores pronósticos de la mortalidad por cáncer de mama. MEDISAN. 2017;21(4): 413. [citado 10 Ene 2018]; Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1029-30192017000400003 27.

28.  Moraga Rodríguez A, Zamora Matamoros L, Sagaró del Campo NM, Moraga Rodríguez A, Rodríguez Griñán A. Análisis estadístico implicativo para la identificación de factores pronósticos de la mortalidad por cáncer de próstata. MEDISAN. 2018;22(1). [citado 10 Ene 2018]; Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1029-30192018000100007 28.

29.  Paez Candelaria Y, Sagaró del Campo NM, Zamora Matamoros L. Análisis estadístico implicativo en la determinación de factores pronósticos del estado nutricional del paciente grave al egreso. MEDISAN 2018;22(6). [citado 10 Ene 2018]; Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1029- 29.

Recibido: 12 de Febrero de 2019; Aprobado: 27 de Mayo de 2019

^*Autor para la correspondencia: e-mail: [e-mail]