Introducción
La mayoría de los problemas de investigación en las ciencias biomédicas son de naturaleza causal. El primer paso en el estudio de la causalidad es buscar la posible asociación entre las variables que se consideran causa y efecto, y solo si se encuentra asociación significativa entre ellas podrá continuar el análisis de inferencia causal.1
Dos variables se relacionan entre sí cuando el cambio de una categoría a otra (para variables cualitativas) o de un valor a otro (para variables cuantitativas), provoca una modificación en las categorías o valores de la otra variable; en caso contrario se dirán independientes.
El análisis estadístico que identifica una posible relación entre variables es una forma básica de análisis de datos y según el tipo de variable puede llamarse asociación o correlación. Suele llamarse asociación cuando se busca la relación entre variables categóricas, de manera que sus categorías puedan colocarse en tablas de contingencia, y correlación cuando se relacionan variables en escala de intervalo o de razón o incluso, en escala ordinal y en vez de analizarla por tablas de contingencia, se les asignan rangos a las categorías convirtiéndose en numéricas.
Estas relaciones entre las variables pueden ser:
Relaciones simples: entre dos o tres variables aleatorias en la cual se establece:
Relación bivariada: relación entre dos variables (X, Y) donde X y Y son medidas en cualquier escala.
Relación bivariada con influencia de una tercera variable que puede ser:
Relación transicional: cuando la variable Y, dependiente en una relación bivariada (X, Y) es la independiente respecto a otra relación bivariada (Y, Z) [X→Y→Z].
Interferencia de una o varias variables intervinientes: cuando una tercera variable (Z) provoca cambios importantes en la relación (X, Y).
Correlación parcial: correlación entre dos variables eliminando los efectos de otra variable interviniente.
Relaciones múltiples: cuando se correlacionan múltiples variables aleatorias, generalmente existe una variable aleatoria dependiente y un vector aleatorio independiente, formado por las covariables e incluye variantes como:
En una relación entre variables se examina la intensidad por el valor del estadígrafo y el sentido por su signo. Además, para conocer la significación de la relación siempre se deben realizar contrastes de hipótesis. En el caso de las variables cuantitativas se examina, además, la forma en que se relacionan, la cual puede observarse gráficamente en un plano cartesiano o puede ser expresada matemáticamente. Esta expresión es importante para explicar e incluso, predecir lo que pasará en la variable dependiente en función de los cambios en la independiente.
Existe una gran variedad de coeficientes y pruebas paramétricas y sobre todo, no paramétricas para corroborar la significación de una relación encontrada, estos se emplean en dependencia del tipo de variables y la cantidad y tipo de muestra si fuera el caso.2
Por la importancia que tiene para todo investigador el conocimiento de estas técnicas se gestó este trabajo con el objetivo de sistematizar las diferentes técnicas estadísticas para verificar la relación entre variables según su tipo.
Métodos
En este estudio se abordan solo las relaciones bivariadas clásica y con la influencia de una tercera variable. La investigación se desarrolló con una exhaustiva revisión de la literatura sobre el tema en las bases de datos bibliográficas alojadas en la Internet como Pubmed/Medline, EMBASE, SCOPUS, Web of Science, EBSCOhost y Google Académico, en el período entre enero y abril de 2019. Se emplearon en la estrategia de búsqueda como descriptores los consignados en las palabras claves del artículo, estos fueron utilizados en idiomas inglés, francés, portugués y español, combinados con los operadores lógicos. Se escogieron los artículos publicados en revistas arbitradas o repositorios de Universidades, cuyo período de publicación fuera, en lo posible, menor de 10 años y se relacionaran con la medición en salud. Se organizó el contenido por subtemas y se elaboró un material con una síntesis crítica de los aspectos más importantes, en el cual se plasmó, además, la experiencia de las autoras.
Técnicas estadísticas según tipo de variables
Se expone a continuación, información básica de los coeficientes, pruebas de hipótesis y gráficos empleados, según tipo de variables. Las fórmulas y otros detalles de los coeficientes expuestos se pueden consultar en las bibliografías citadas.
Relación entre variables cuantitativas
La relación entre dos variables cuantitativas puede medirse por la covariación, pero esta depende de las unidades de medida de las variables y no está acotada, por lo que se prefiere el uso de los coeficientes de correlación que permiten medir la fuerza y la dirección de la asociación entre ambas variables. Entre estos están:
El coeficiente de correlación producto-momento de Pearson: coeficiente paramétrico que solo puede calcularse para variables con niveles de medición intervalar o de razón.3
Los coeficientes de correlación no paramétricos Rho de Spearman y Tau de Kendal o por rangos de Kendall: estos no requieren para su empleo que la distribución muestral ajuste a una distribución conocida, por lo que los estimadores muestrales no son representativos de los parámetros poblacionales. Se emplean también para variables medidas en escala ordinal. Se calculan en base a una serie de rangos asignados por lo que no se afectan por valores atípicos y son apropiados para relaciones asimétricas, no lineales.
Los valores de estos coeficientes oscilan de (1 a 1, siendo los valores extremos los que indican la mayor correlación y el 0 la ausencia de correlación. El signo del coeficiente indica el sentido de la relación. Ante un signo positivo se dirá que la relación es directa (las variables cambian en el mismo sentido) y ante uno negativo se dirá que es inversa (a medida que aumenta una disminuye la otra).4,5
La interpretación del valor del coeficiente puede darse con mayor detalle por intervalos. Diferentes son los intervalos que han establecido algunos autores para considerar la correlación débil, moderada o fuerte, lo cual aplica igual en el caso de un valor negativo. Incluso ciertas literaturas incluyen intervalos no excluyentes como esta guía de la Universidad de Chile de Ciencias Sociales que plantea que un valor entre 0 y 0,2 indica una correlación mínima; entre 0,2 y 0,4, una correlación baja; entre 0,4 y 0,6, moderada, entre 0,6 y 0,8 buena y entre 0,8 y 1 muy buena.5
Es importante tener presente algunos aspectos en el estudio de la correlación entre variables:
La correlación no implica causalidad. La causalidad es un juicio de valor que requiere más información.
No necesariamente existirá dependencia entre ambas variables, ya que una correlación puede deberse a una covariación conjunta determinada por una tercera variable
Estos coeficientes solo miden correlación monótona y lineal. Para medir una relación curvilínea se emplea la proporción de correlación representada por el coeficiente eta.6
Tampoco son apropiados para medir concordancia, en este caso se emplea el método gráfico de Bland y Altman o el coeficiente de correlación intraclase que estima el promedio de las correlaciones entre todas las posibles ordenaciones de los pares de observaciones disponibles.7 Ambos métodos pueden interpretarse como una medida de fiabilidad.8,9
El gráfico más adecuado para apreciar la relación entre dos variables numéricas es el diagrama de dispersión. Este que consiste en plotear los pares de valores de las variables de cada unidad de observación en el plano cartesiano, formando una nube de puntos que puede adoptar diferentes formas las cuales ofrecen idea del tipo de relación (asemeja una recta cuando existe correlación lineal o una curva para una relación curvilínea) o sin forma específica que indica la independencia entre las variables.3
En el caso de darse una correlación lineal con dependencia entre las variables es posible estimar la recta que mejor describe esta relación entre ambas variables mediante la regresión lineal simple y mediante el coeficiente de determinación que evaluará el ajuste de los datos a la recta obtenida.10
Relación entre variables ordinales
Una relación entre dos variables ordinales se da cuando los cambios en el orden de las categorías de una variable influyen en el orden de las categorías de la otra variable. En este caso se emplean coeficientes no paramétricos que trabajan con rangos y se basan en el concepto de inversión y no‐inversión.11 Una relación positiva o de “no inversión” habla de un predominio de asociación entre los rangos altos de una variable con los rangos altos de la otra al igual que entre los rangos bajos de ambas variables. En cambio, una relación negativa (inversión) habla de un predominio de asociación entre los rangos altos de una variable con los bajos de la otra. Si las variables son independientes habrá tantas inversiones como no inversiones y el coeficiente valdrá cero; sin embargo, un valor de cero no implica necesariamente que sean independientes.4
Entre estos coeficientes están:
Rho de Spearman empleado para comparar dos conjuntos de rangos ordenados en una muestra o dos grupos con los rangos ordenados de varias unidades de análisis.12
Tau b de Kendall empleado para comparar dos rangos cuando se tiene un par de rangos por cada unidad de observación. Es solo aplicable en tablas de contingencia cuadradas (igual número de filas que de columnas) y si ninguna frecuencia marginal tiene valor cero en sus casillas; no llega a valer 1 si la tabla no es cuadrada.12
Tau c de Kendall que supera las dificultades del tau b.
Gamma de Goodman y Kruskal.
d de Somers. Este tiene una versión simétrica que coincide con el Tau-b de Kendall y una asimétrica, modificación del gamma, que considera a las variables como dependiente e independiente.12
El Gamma se emplea para identificar la relación entre dos variables cuando al menos una variable es ordinal. Spearman y Kendall pueden emplearse cuando ambas son ordinales o en escala intervalar.
Todos estos coeficientes arrojan resultados entre -1 y 1, excepto la versión asimétrica del d de Sommer.12 Todos se basan en los conceptos de inversión y no inversión, la diferencia entre ellos está en el tratamiento que dan a los empates (cuando los pares no son de tipo inversión ni no inversión ya que los rangos en ambas variables coinciden).
Para conocer la concordancia entre dos o más observadores es posible emplear una versión del coeficiente de Kendall y el W de concordancia de Kendall.
Relación entre una variable continua y una nominal
Las técnicas empleadas para estudiar la relación entre una variable continua y una nominal varían en dependencia de la variable cualitativa nominal y las características de las muestras en estudio.
Si la variable cualitativa es politómica se pueden emplear el coeficiente de correlación esta que no supone linealidad y cuyo cuadrado puede interpretarse, si el diseño lo permite, como la proporción de varianza de la variable cuantitativa que es explicada por la variable categórica15 o el índice f de Cohen cuyo valor mide la intensidad de la asociación.3
En cambio, si la variable es dicotómica se podrán emplear el coeficiente biserial puntual, los índices delta de Glass, g de Hedges, d de Cohen o el índice d, modificación del índice d de Cohen para el caso de una medición repetida en dos momentos para un mismo grupo.3
Estos índices son muy empleados para determinar el llamado tamaño del efecto que se produce en grupos bajo diferentes tratamientos en estudios experimentales o en el metaanálisis de investigaciones cuyo efecto cuantitativo se obtuvo por la media.13
A veces las categorías de una variable cualitativa se forman a partir del empleo en la investigación de más de una muestra, en este caso lo que se pretende es buscar diferencias entre ellas. Si las diferentes categorías de la variable politómica representan los niveles donde se mide la variable cuantitativa se debe emplear el análisis de varianza paramétrico o el no paramétrico de Kruskal Wallis. Dada una dicotomía condicionada por dos muestras independientes se pueden emplear las pruebas de comparación de media en muestras independientes t de student sin o con la aproximación de Welch, en dependencia de si existe o no homocedasticidad de varianzas, respectivamente; o sus alternativas no paramétricas, la U de Mann y Withney, las rachas de Wald Wolfowitz, entre otros. Si la dicotomía es condicionada por muestras pareadas se debe emplear la t de student para muestras pareadas o sus alternativas no paramétricas el test de los signos, el de rangos con signos de Wilcoxon, entre otros.6
El empleo de una prueba paramétrica siempre dependerá del cumplimiento de supuestos como la independencia, normalidad y homocedasticidad de las varianzas.14 El supuesto de independencia puede corroborarse mediante el test de Durbin Watson, el de normalidad a través de técnicas gráficas como el histograma, los gráficos de probabilidad normal P-P y de cuantiles normales Q-Q o con técnicas estadísticas como las pruebas de bondad del ajuste de Kolmogorov-Smirnov, Shapiro-Wilk, D’Agostino, Lilliefors, entre otros o el cálculo de los coeficientes de simetría y de curtosis, mientras que la igualdad de varianzas se verifica con los test de Levene, Barttle o C de Cochran.
Los gráficos empleados para representar esta información son los polígonos de frecuencia, donde se podrá comparar el grado de solapamiento de las distribuciones de la variable cuantitativa condicionadas por las categorías de la cualitativa y en el análisis exploratorio de los datos se emplean las gráficas de cajas y bigotes o las de barras de error múltiples con la distribución de la variable cuantitativa condicionada a la variable cualitativa (una caja o barra por cada categoría de la variable nominal).15
Relación entre variables cualitativas
Para identificar la posible relación entre dos variables cualitativas hay que observar si la distribución de las categorías de una de las variables difiere en función de las de la otra, o sea comparar las distribuciones condicionadas de una de las dos variables agrupadas en función de los valores de la otra. Si no hay relación entre las variables estas distribuciones deberían ser iguales.15
Habitualmente se colocan los datos en una tabla de contingencia o de doble entrada, donde aparecen las frecuencias observadas (frecuencias absolutas conjuntas o número de casos que presentan simultáneamente las modalidades fila y columna) y se emplean métodos directos como el análisis de los residuos de la diferencia entre valores observados y esperados o la descomposición de la tabla en tablas de 2 × 2.12
Esta relación se mide a través de los llamados coeficientes de contingencia tales como:
Coeficientes basados en la reducción de error como Lambda, Tau de Goodman y Kruskal y el coeficiente de incertidumbre de Theil.2
Coeficientes simétricos basados en chi cuadrado como:
El T de Tschuprow.
El de contingencia C de Pearson (solo para tablas cuadradas inicialmente y corregido por Pawlik superando esta dificultad).2
Si al menos una de ellas es binaria se puede emplear el coeficiente de contingencia V de Cramer.
En el caso que ambas sean dicotómicas se emplea el coeficiente Phi de Pearson.
Para las tablas de 2 × 2 existen muchísimos más coeficientes como el Q de Yule, J de Youden, de Forbes, de McConnaughy, de Michel, de Simpson, de Baroni-Urbani y Buser, de Agrell e Inverson, de Mountford, de Dice, entre otras.16
Si se quiere determinar la concordancia entre instrumentos de medida cuyo resultado es categórico se emplea el índice de Kappa de Cohen que depende del acuerdo observado, pero también de la prevalencia del carácter estudiado y de la simetría de los totales marginales.17
Para demostrar la significación de esta asociación solo se emplean pruebas no paramétricas como las siguientes:
Chi cuadrado.
G2 de razón de verosimilitud.
Para tablas de 2 × 2 puede emplease el test exacto de probabilidades de Fisher, sobre todo en muestras menores de 20 y válido para variables ordinales también si la muestra es pequeña.18 Este aumenta su potencia con la modificación propuesta por Tocher.
Si la dicotomía es producto de muestras pareadas se emplea la prueba de McNemar.18
Si se quiere controlar el efecto de una tercera variable, se analizan ambas variables dicotómicas dentro de los estratos de esa tercera, mediante la prueba de Cochrane Mantel Haenszel.
Una mención aparte merece la más empleada de estas técnicas, la chi cuadrado, llamada de independencia cuando la tabla se genera a partir de una muestra o de homogeneidad si se genera por más de una muestra y se fijan entonces esos totales marginales por fila (estudios de casos y controles) o por columna (estudios de cohortes o ensayos clínicos controlados). Esta prueba solo mide la significación de la asociación, pero no constituye una medida de intensidad de la asociación, porque en su cálculo involucra el tamaño de muestra (depende no solo de las proporciones totales sino también del gran total), tampoco permite conocer el sentido de la asociación pues al estar el estadígrafo elevado al cuadrado su valor siempre será positivo. El test no se puede emplear si en más de 20 % de las celdas de la tabla hay valores esperados menores que 5 o en una sola celda hay un valor menor que 1. Para aumentar estas frecuencias se sugiere agrupar las categorías siguiendo un sentido lógico siempre que sea posible o emplear el test de Fisher en tablas de 2 × 2. Otro aspecto a considerar en las tablas de 2 × 2 es el empleo de la corrección de Yates atenuando el efecto de usar una distribución continua para representar una distribución discreta y evitar encontrar diferencias muestrales que no existen a nivel poblacional (dificultar el rechazo de la hipótesis nula).11
La representación gráfica de la relación entre variables categóricas puede obtenerse mediante barras múltiples o barras proporcionales. En las barras se deben representar las frecuencias relativas condicionadas y no las frecuencias absolutas, pues así se elimina el efecto de la diferencia de tamaño entre los subgrupos.3
Validez de una asociación
Para que una asociación sea válida (real o verdadera) hay que tener en cuenta el efecto de dos errores que pudieran cometerse en el proceso de investigación: el azar (error aleatorio) y el sesgo (error sistemático).
La influencia del azar se puede determinar por dos vías:
Las pruebas de significación estadística, donde la significación está dada por el valor de p. Si una prueba de asociación arroja como resultado un valor de p mayor que el nivel de significación alfa prefijado, habitualmente de 5 %, no es posible asegurar que existe asociación entre las variables, aun cuando el valor del coeficiente así lo indique, porque la probabilidad de estar equivocado al señalar que existe asociación es muy alta.19
Los intervalos de confianza, como por ejemplo, al 95 % reflejan los resultados que se esperarían obtener en 95 de 100 repeticiones del mismo estudio, por lo que no excluyen la posibilidad de que exista dicha asociación y es posible que proporcionen cierta información sobre su magnitud, en especial en estudios pequeños.20
Ambas informaciones son complementarias y dependientes del tamaño de la muestra, de manera que, a menor tamaño de muestra, mayor es el valor p y más amplio el intervalo. Por otro lado, los sesgos pueden incidir en la obtención de una asociación que no existe o hacerla mayor de lo que es. Estos sesgos pueden ocurrir en cualquier fase del proceso de investigación y pueden ser de tres tipos.21
De selección: por una selección de los sujetos en estudio de manera diferencial entre grupos o de manera no representativa de la población que les da origen, por ejemplo: a) el sesgo de Berkson, que se produce en los estudio de casos y controles realizados en los hospitales, donde la probabilidad de ser incluido como caso es mayor, por lo que se producirá una sobrestimación de la asociación, b) pérdidas durante el seguimiento relacionadas con el factor de estudio o la variable de respuesta (pérdidas informativas), c) ausencia de respuesta que prevalece en relación con determinada variable, d) supervivencia selectiva que se produce cuando se seleccionan casos prevalentes en lugar de incidentes, típico en los estudios de casos y controles y e) el sesgo de autoselección por participación de voluntarios.
De medición: sucede durante la fase de obtención de información por empleo de criterios diferentes para la recolección de datos y clasificación de los grupos en estudio o cuando los métodos de medición para establecer las conclusiones se emplean de manera diferencial entre los grupos, por ejemplo en el uso de pruebas de detección de un efecto, cuya sensibilidad y especificidad varían en función de la exposición y el grado de asociación (que dependerá del número de resultados falsos positivos y negativos determinado por cada prueba).También se puede presentar el sesgo de memoria en el sujeto que no recuerda el dato o del entrevistador que influye en la respuesta.
De confusión: se produce cuando no se tiene en cuanta alguna variable responsable de la falsa asociación encontrada, que es el verdadero factor de riesgo pronóstico y es causa común del falso factor de riesgo o pronóstico y el desenlace.
El efecto del azar es imposible de controlar porque es inherente al muestreo, en cambio los sesgos se atenúan con un adecuado rigor metodológico en el estudio.
Medidas de asociación ligadas al riesgo de desarrollar un efecto frente a una exposición
La fuerza de asociación es la magnitud con que aumenta el riesgo de desarrollar un efecto cuando se presenta una exposición. A mayor fuerza de asociación es mayor la seguridad sobre la causalidad. Las tres medidas más empleadas en los estudios de causalidad en relación con este riesgo son:22,23
Riesgo relativo (RR) que es la razón entre el riesgo de los expuestos (incidencia del efecto en los expuestos) y el riesgo de los no expuestos (incidencia del efecto en los no expuestos). Es la medida que refleja mejor la probabilidad de padecer la enfermedad en función de la exposición.
Esta medida es aplicable a los estudios prospectivos, ya sean experimentales (ensayos aleatorios) u observacionales (de cohorte), donde es posible estimar la incidencia del efecto. En los estudios de casos y controles se utiliza una estimación indirecta del riesgo relativo, a través de la razón de productos cruzados o razón de momios, más conocida como odds ratio y en los transversales la medida de asociación equivalente es la razón de prevalencias para enfermedades agudas y la razón de momios de prevalencia para enfermedades crónicas.
Un RR mayor de 1 tiene significación estadística y uno mayor de 3 tiene además significación clínica, pues implica un riesgo de desarrollar el efecto tres o más veces, mayor en los sujetos expuestos, que en los no expuestos.24Silva25 plantea que para algunos autores un RR mayor que 2 es suficiente para considerar una relación fuerte.
Riesgo atribuible o diferencia de riesgos, la cual permite distinguir el efecto absoluto de la exposición y expresa la proporción de individuos expuestos que, por efecto de la exposición, desarrollarán el efecto. Consiste en restar al riesgo en expuestos, el riesgo en no expuestos. El resultado será la proporción de enfermedad que podrá disminuirse al eliminar el factor de riesgo. Se le reconocen dos limitaciones: 1) no puede estimarse en los estudios de caso y controles ya que solo puede utilizarse cuando se estima alguna medida de frecuencia como la prevalencia en un estudio transversal analítico o la incidencia en un estudio de cohorte y 2) puede subestimar la proporción de riesgo.
Fracción etiológica o porcentaje de riesgo atribuible, que permite estimar la proporción del riesgo o el efecto observado en los sujetos expuestos, que es atribuible a la exposición. Se puede estimar para los individuos expuestos denominado riesgo atribuible en expuestos y para la población denominado riesgo atribuible poblacional, a partir de la medida de asociación calculada según el tipo de estudio.
El riesgo atribuible y la fracción etiológica se consideran medidas del impacto potencial porque sirven para evaluar la efectividad de las acciones del personal de salud para atenuar o erradicar los supuestos factores de riesgo identificados tanto en los expuestos como en la población en general.15
Hace algunos años, era común emplear las tablas de 2 × 2 para organizar los datos procedentes de los estudios de causalidad, en la cual solo es posible analizar la relación entre dos variables. En sus columnas cuentan los individuos que poseen y no poseen la característica en estudio, generalmente la enfermedad o desenlace fatal y en sus filas, los expuestos y los no expuestos al supuesto factor de riesgo o pronóstico. Las medidas anteriores se pueden calcular a partir de los valores de las celdas de esta tabla. Sin embargo, en la actualidad, en correspondencia con el paradigma multicausal imperante se emplean técnicas de análisis multivariado y la medida de asociación se obtiene con la aplicación de la regresión logística binaria a partir del valor de la exponencial del coeficiente de regresión asociado a cada factor. Este análisis no solo permite fortalecer el argumento de la causalidad entre un factor de riesgo o pronóstico y un desenlace específico, además ayuda a un mejor reconocimiento y tratamiento de variables confusoras y modificadoras del efecto. En Sagaró y Zamora26 se precisan detalles de la evolución histórica de las técnicas estadísticas para el estudio de la causalidad donde se distingue el paso de las técnicas bivariadas a las multivariadas.
La asociación en el análisis estadístico implicativo
Las medidas que reflejan la relación entre variables en el análisis estadístico implicativo son:27,28,29,30,31,32
El índice de implicación: indicador de la no implicación de una variable a sobre otra variable b. Este índice es no simétrico y no coincide con el coeficiente de correlación u otros índices simétricos que miden asociación.
El índice de implicación-inclusión o de implicación entrópica: versión entrópica del índice de implicación que supera la poca discriminación de este en muestras grandes. Este índice permite determinar el criterio entrópico al integrar la información a partir de la presencia de un escaso número de contraejemplos, tanto por la regla
 como por su negación
como por su negación 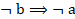 .
.
La representación gráfica de la relación se visualiza en el grafo implicativo, donde el sentido de la flecha orienta al investigador para generar hipótesis de causalidad. Este grafo es similar a los diagramas causales del tipo grafo acíclico dirigido que permiten plantear posibles rutas de asociación entre causas y efectos, así como otras rutas alternativas que pueden ocasionar sesgos por lo que facilitan también el control de posibles sesgos.33,34,35,36,37,38
Conclusiones
El conocimiento de los estadísticos a emplear para verificar una relación entre variables es esencial para llevar a cabo el proceso inicial de inferencia causal. La selección de una prueba o coeficiente dependerá del tipo de variable, además el empleo de un test paramétrico conlleva el cumplimiento de supuestos como la normalidad, independencia y homocedasticidad de varianzas. Las pruebas no paramétricas se emplean para muestras pequeñas, variables cualitativas o no cumplimiento de los supuestos. Independientemente de que se obtenga un valor alto en un coeficiente debe verificarse la significación del mismo, de lo contrario no es posible hablar de asociación y aun cuando se obtenga significación estadística esto no es siempre equivalente a una asociación en la práctica médica, esta conclusión solo puede lograrse con la lógica y experticia del investigador.
Otro aspecto en las relaciones bivariadas son las medidas específicas a emplear en estudios epidemiológicos y el control de errores potenciales desde el momento del diseño de la investigación.
Por último, se destaca que mediante el análisis estadístico implicativo es posible obtener las relaciones entre variables de manera visual, lo cual pudiera resultar muy atractivo para el investigador.














