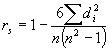Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Habanera de Ciencias Médicas
versión On-line ISSN 1729-519X
Rev haban cienc méd v.8 n.2 Ciudad de La Habana abr.-jun. 2009
Instituto Superior de Ciencias Médicas de La Habana (ISCM-H)
Facultad de Ciencias Médicas Dr. Enrique Cabrera
EL COEFICIENTE DE CORRELACION DE LOS RANGOS DE SPEARMAN
CARACTERIZACION
*Lic. Rosa María Martínez Ortega. Calle E entre 7ma. y Paseo. Edificio 15059. Apto 3. Altahabana. Boyeros. Ciudad de La Habana. Teléfono: 6446315 ó 6434172.
rosy@fcmec.sld.cu rosy@infomed.sld.cu
** Lic. Leonel C. Tuya Pendás. Avenida 83 núm.11414 entre 114 y 116. Marianao. Ciudad de La Habana. Teléfono: 2670866. leonel@fcmec.sld.cu ltp@infomed.sld.cu
*** Lic. Mercedes Martínez Ortega. Calle E entre 7ma. Y Paseo. Edificio 15059. Apto 3. Altahabana. Boyeros. Ciudad de La Habana. Teléfono: 6446315. mercedesmtnez@infomed.sld.cu
**** Lic. Alberto Pérez Abreu. Larcada núm.11904 entre Cotilla y Aldabó. Rpto. Aldabó Ciudad de La Habana. alberto@fcmec.sld.cu apabreu@infomed.sld.cu
***** ATD. Ana María Cánovas. Calle Quintana núm. 13610 entre 4ta. y 5ta. Aldabó. Apto 16. Altahabana. Ciudad de La Habana. Teléfono: 6447678
acanovas@fcmec.sld.cu anacanovas@infomed.sld.cu
*Auxiliar de Bioestadística.
*Auxiliar de Bioestadística
***Lic. en enfermería. Instructora.
****Profesor de Informática médica.
*****Auxiliar técnico de la docencia de Informática médica.
En el ámbito de las investigaciones clínico-epidemiológicas, los profesionales de la salud asiduamente se proyectan en sus investigaciones; se definen las relaciones entre las características de un fenómeno, el grado de esa relación o probar la confiabilidad de sus observaciones, planteándose como hipótesis si estas son o no la causa de una determinada entidad. En la práctica, generalmente, acontece que el investigador entre las disímiles pruebas estadísticas de las que dispone, no selecciona adecuadamente la que con mayor cientificidad le aportará una lectura fácil de dicha relaciones. Se realiza una revisión bibliográfica con el objetivo de caracterizar el método de correlación de rangos de Spearman, utilizado para valorar la asociación entre variables cuantitativas, aplicándose el método de análisis documental .Los resultados son declarados al resumir la historia del surgimiento de la teoría de la correlación y la regresión, explicación de conceptos asociados, su presentación gráfica, los rasgos esenciales del algoritmo de solución tradicional y con asesor estadístico, así como una compilación sobre escalas de interpretación de la prueba estadística. Se proyecta que el trabajo realizado sirva de bibliografía a consultar por investigadores y estudiantes de las Ciencias Médicas.
Palabras clave : Correlación, Spearman, Pearson, Correlación de Spearman, estadística, regresión, correlación lineal, coeficiente de correlación, rangos, psicología diferencial, historia
INTRODUCCION
El conocimiento humano transita de lo general a lo particular y, en este, sus relaciones, las que explican fenómenos nuevos generados por la relación entre eventos de un mismo fenómeno o fenómenos diferentes. Existen métodos en la ciencia de la Estadística que permiten medir la relación entre dos variables cuantitativas. En las investigaciones surge muy frecuentemente la necesidad de determinar la relación entre dos variables cuantitativas en un grupo de sujetos. Los objetivos suelen ser:
- Determinar si las dos variables están correlacionadas, es decir, si los valores de una variable tienden a ser más altos o más bajos para valores más altos o más bajos de la otra variable.
- Poder predecir el valor de una variable, dado un valor determinado de la otra variable.
- Valorar el nivel de concordancia entre los valores de las dos variables. 1
Generalmente, en la comunidad de estadísticos e investigadores existe una tendencia a calcular el coeficiente de correlación Pearson para determinar el grado de variación de una variable con respecto a otra en un grupo de sujetos, basados en la eficiencia de la correlación de rango de Spearman, cuando se compara con la correlación paramétrica , la de Pearson, es de cerca de 91 por ciento, es decir : ”Si existe una correlación entre X y Y en esa población el rango de Spearman necesitará 100 casos para establecer correlación al mismo nivel de significación que el rango de Pearson, logra con 91 casos.” 2 Marcados por este criterio, ponemos a disposición de la comunidad científica la elección y comparación de los dos métodos para calcular la dirección de la relación que se establece entre dos variables en estudio.
Nuestra revisión transitó en el análisis de documentos impresos y en línea, filtrando la información por grupos temáticos, asociados con historia de la regresión y la correlación; biografía de Charles Edward Spearman y Carl Pearson; términos asociados, algoritmo de solución, presentación gráfica y escalas de interpretación, en las que se establecieron los rasgos más comunes de las bibliografías consultadas, mostrando en varios ejemplos cómo el resultado final de ambos métodos no tienen diferencias significativas.
DESARROLLO
La teoría de la correlación y la regresión son muy recientes y su descubrimiento se debe al médico inglés Sir Francis Galton. Galton nació en 1822 en Birminghan en el seno de una familia acomodada. Estudió en Hospital General de Birmingham, en el King's College de Londres y en el Trinity de Cambridge. Sus trabajos se desarrollaron en torno al estudio de la herencia y la expresión matemática de los fenómenos vinculados a ella. El contexto histórico en el que vivió favoreció su interés por la herencia genética: nació el mismo año que George Mendel con el que mantenía una gran afinidad y era primo de Charles Darwin. En 1869, publicó el libro Hereditary Genius, y a través del estudio de problemas de la herencia, llegó al concepto de correlación, siendo el primero en asignar a un conjunto de variables un número que permitía obtener una medida del grado de relación existente entre ellas. Llegó a inferir que las personas excepcional-mente altas solían tener hijos de estatura menor que sus progenitores, mientras que las personas muy bajas solían tener hijos más altos que sus padres. Esta observación llevó a Galton a enunciar su "principio de la mediocridad", aplicable a las tallas de una generación respecto de las siguientes. Este fue el origen del actual análisis de la regresión. La observación de Galton es, sin dudas, cierto, pero el supuesto de la regresión de la mediocridad es totalmente falso y se considera actualmente como una de las falacias de la regresión. La justificación que se da hoy a este hecho es que los valores extremos de una distribución se deben en gran parte al azar; de ahí que los factores genéticos que producen una talla excepcional por exceso o por defecto no pasan a los hijos. Su obra Meteorographica fue el primer intento de previsión del tiempo y, por otra parte, puede ser considerado como el padre de la eugenesia. Los trabajos de Galton fueron continuados y mejorados, entre otros, por Karl Pearson.
Pearson nació en Londres en 1857 y comenzó estudiando derecho. Posteriormente, ejerció la abogacía al tiempo que simultaneaba sus actividades políticas y literarias. A los 27 años comenzó a impartir clases de matemáticas aplicadas en la Universidad de Londres. En 1901, fundó la revista Biométrica, en la que publicó una biografía monumental de Galton. A Pearson se deben aportaciones tan importantes como la distribución ji-dos o el Test de Pearson para el estudio de la bondad del ajuste de una distribución empírica a otra teórica.
Reseña Charles Edward Spearman
(Londres, 1863-1945) Psicólogo británico. Siguió estudios de psicología en Alemania y se doctoró en Leipzig. Fue profesor de mente y lógica en el University College de Londres. En un artículo, publicado en 1904, expuso su teoría bifactorial de la inteligencia, según la cual la ejecución de cualquier actividad mental depende de dos factores distintos, un factor general "g", que es la base común de la inteligencia y que, aunque varía libremente de un individuo a otro, se mantiene igual para cualquiera de ellos respecto de todas las capacidades correlacionadas, y un factor específico "s", que son las aptitudes específicas, que no sólo varían de un individuo a otro, sino también de una capacidad a otra. La noción de un factor general despertó gran interés y mucha controversia. Sperman desarrolló la técnica estadística conocida como análisis factorial, como complemento indispensable de su teoría. También aportó el coeficiente de correlación ordinal que lleva su nombre, que permite correlacionar dos variables por rangos en lugar de medir el rendimiento separado en cada una de ellas. Sus obras más importantes son The nature of intelligence and the principles of cognition (1923) y The abilities of man (1927). 3
Correlación. Conceptos asociados
Regresión: La regresión es una técnica utilizada para inferir datos a partir de otros y hallar una respuesta de lo que puede suceder Se pueden encontrar varios tipos de regresión, por ejemplo:
- Regresión lineal simple.
- Regresión múltiple ( varias variables).
- Regresión logística.
Correlación: Expresa grado de asociación entre dos variables, según el sentido de la relación de estas en términos de aumento o disminución. Se clasifican en:
Lineal o curvilínea, según la nube de puntos se condense en torno a una línea recta o a una curva.
Positiva o directa cuando al aumentar una variable aumenta la otra y viceversa.
Negativa o inversa cuando al crecer una variable, la otra decrece y viceversa.
Nula cuando no existe ninguna relación y la nube de puntos están distribuidas al azar. Se dice que no están correlacionadas.
Funcional si existe una función tal que todos los valores de la nube de puntos la satisfacen.
COEFICIENTE DE CORRELACION
Estadístico que cuantifica la correlación. Sus valores están comprendidos entre -1 y 1
COEFICIENTE DE DETERMINACION
Es el cuadrado del coeficiente de correlación.
RHO DE SPEARMAN
Nombre utilizado para designar la correlación de Spearman. 4
¿Cuándo utilizar la prueba de correlación de rangos de Spearman?
El coeficiente de correlación no debe utilizarse para comparar dos métodos que intentan medir el mismo evento, como por ejemplo dos instrumentos que miden la saturación de oxígeno en sangre. El coeficiente de correlación mide el grado de asociación entre dos cantidades, pero no mira el nivel de acuerdo o concordancia. Si los instrumentos de medida miden sistemáticamente cantidades diferentes uno del otro, la correlación puede ser 1 y su concordancia ser nula . El coeficiente de correlación de Spearman es recomendable utilizarlo cuando los datos presentan valores extremos, ya que dichos valores afectan mucho el coeficiente de correlación de Pearson, o ante distribuciones no normales. No está afectada por los cambios en las unidades de medida. 5
Coeficiente de correlación de rangos de Spearman
Como resultado de la revisión de varios autores, asumimos el siguiente concepto:
SPEARMAN (Rho de Spearman). Este coeficiente es una medida de asociación lineal que utiliza los rangos, números de orden, de cada grupo de sujetos y compara dichos rangos. Existen dos métodos para calcular el coeficiente de correlación de los rangos: uno, señalado por Spearman y otro, por Kendall. El r de Spearman llamado también rho de Spearman es más fácil de calcular que el de Kendall. 5
Fórmula
en donde d i = r xi – r yi es la diferencia entre los rangos de X e Y.
Otra variante de la fórmula expresada es: 6![]()
Algoritmo de solución : Observando el criterio de estadísticos actuales, la mayoría confluye en el siguiente algoritmo de trabajo: Los valores de los rangos se colocan según el orden numérico de los datos de la variable. Por ejemplo, si tenemos las siguientes variables:
Talla Peso
1,68 68
1,89 70
1,75 80
1,56 45
1,48 48
Al convertirlas en una escala ordinal, obtendríamos los resultados:
Talla Peso
3 3
5 4
4 5
2 1
1 2
El primer valor de talla (en este caso 1,68) se convierte en 3, porque el 1,68 es el tercer valor más pequeño de la talla. El valor en peso de 45 se convierte en 1, porque es el menor –Luego se calculan las diferencias de rangos
d i d i 2
3-3 0
5-4 1
4-5 1
2-1 1
1-2 1
--------
4
Interpretación: En la muestra observada los valores de talla y peso tienen una correlación entre fuerte y perfecta, lo que se traduce que en la medida que aumentan los valores de la talla también aumentan los del peso y viceversa.
Correlación de Pearson y Correlación de Spearman
El coeficiente de correlación de Spearman es exactamente el mismo que el coeficiente de correlación de Pearson, calculado sobre el rango de observaciones. La correlación estimada entre X e Y se halla calculando el coeficiente de correlación de Pearson para el conjunto de rangos apareados. La correlación de Spearman puede ser calculada con la fórmula de Pearson, si antes hemos transformado las puntuaciones en rangos. 8
Presentación de la correlación
Se recomienda a los investigadores realizar primero una representación gráfica de la correlación, con dos objetivos fundamentales: 7
- Que visualice el tipo de relación que se establece en las variables.
- Para corroborar el resultado matemático obtenido.
El gráfico por excelencia es el diagrama de dispersión, debido a que la posición de puntos materializa si la relación es lineal a través precisamente de una línea de fácil observación por el investigador. En el mismo, la variable independiente se coloca en el eje de las abscisas y la dependiente en el eje de las ordenadas. El valor de r se debe mostrar con dos decimales junto con el valor de la p, si el test de hipótesis se realizó para demostrar que r es estadísticamente diferente de cero. El número de observaciones debe a su vez estar indicado. (Figura 7).
La relación entre dos variables cuantitativas queda representada mediante la línea de mejor ajuste, trazada a partir de la nube de puntos. Los principales componentes elementales de una línea de ajuste y, por lo tanto, de una correlación, son la fuerza, el sentido y la forma. La fuerza mide el grado en que la línea representa la nube de puntos: si la nube es estrecha y alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos tiene una tendencia elíptica o circular, la relación es débil. El sentido mide la variación de los valores de B con respecto a A: si al crecer los valores de A lo hacen los de B, la relación es positiva; si al crecer los valores de A disminuyen los de B, la relación es negativa. La forma establece el tipo de línea que define el mejor ajuste: la línea recta, la curva monotónica o la curva no monotónica. 5
Correlación y asesor estadístico SPSS
Los asesores estadísticos de la actualidad, procesan grandes bases de datos, en un tiempo extraordinariamente breve, por lo que recomendamos la utilización de los mismos para optimizar el tiempo del que dispone el investigador para el análisis de los datos. Proponemos el Paquete Estadístico para Ciencias Sociales (SPSS).Pasos a seguir en el asesor
Crear la base de datos
- Realizar un gráfico de dispersión.
- Gráficos.
- Dispersión.
- Simple.
- Definir.
- Asignar las variables en los ejes X y Y. (Anexos 1 a 3).
- Realizar el cálculo del coeficiente de correlación.
- Analizar.
- Correlación.
- Divariada.
- Seleccionar las variables.
- Marcar Pearson y Spearman para comparar si las diferencias son significativas.
- Observar e interpretar los valores. (Anexos 4 a 6).
Interpretación de la correlación
En la interpretación de la prueba estadística correlación de Spearman, es necesario tener en cuenta el objetivo de la investigación que se define en primera instancia y la relevancia de estas relaciones en el fenómeno clínico que se estudia, no depende en nuestras conclusiones solamente de la cifra matemática obtenida, sino basarnos en experiencias científicas del tema de investigación, para evitar que interfiera la casualidad. La explicación de un coeficiente de correlación como medida de la intensidad de la relación lineal entre dos variables es puramente matemática y libre de cualquier implicación de causa-efecto. El hecho de que las dos variables tiendan a crecer o decrecer juntas no indica que la una tenga un efecto directo o indirecto sobre la otra. Ambas pueden estar influidas por otras variables de modo que se origine una fuerte relación matemática. La interpretación de rho depende principalmente de los detalles de la investigación y la experiencia propia en el tema de estudio. La experiencia previa sirve generalmente como base de comparación para determinar si un coeficiente de correlación es digno de ser mencionado.
Diversos autores expresan escalas de interpretación, que se ofrecen a continuación:
Escala 1: El coeficiente de correlación oscila entre –1 y +1, el valor 0 que indica que no existe asociación lineal entre las dos variables en estudio. 9
Escala 2:
Correlación negativa perfecta………………………….. -1
Correlación negativa fuerte moderada débil…………… -0,5
Ninguna correlación……………………………………. 0
Correlación positiva moderada Fuerte…………………. +0,5
Correlación positiva perfecta…………………………... + 1 1
Escala 3:
1) Perfecta R = 1
2) Excelente R = 0.9 < = R < 1
3) Buena R = 0.8 < = R < 0.9
4) Regular R = 0.5 < = R < 0.8
5) Mala R < 0.5 (6)
Escala 4: Rango Relación
0 – 0,25: Escasa o nula
0,26-0,50: Débil
0,51- 0,75: Entre moderada y fuerte
0,76- 1,00: Entre fuerte y perfecta 5
Consideraciones de la interpretación
A modo de conclusión, recomendamos que al interpretar la prueba de correlación de rangos de Spearman debemos tener en cuenta que:
- La interpretación del coeficiente rho de Spearman concuerda en valores próximos a 1; indican una correlación fuerte y positiva. Valores próximos a –1 indican una correlación fuerte y negativa. Valores próximos a cero indican que no hay correlación lineal. Puede que exista otro tipo de correlación, pero no lineal. Los signos positivos o negativos solo indican la dirección de la relación; un signo negativo indica que una variable aumenta a medida que la otra disminuye o viceversa, y uno positivo que una variable aumenta conforme la otra también lo haga disminuye, si la otra también lo hace.
- El personal de salud que investiga debe estar atento a correlaciones que se encuentran en los valores aproximados a +0,95 o superiores, pues en el campo biológico y en especial con datos humanos, correlaciones tan altas, son excesivamente buenas para ser ciertas. Si se obtienen valores mayores o menores que 1, los cálculos deben ser revisados pues se incurrió en un error de proceso . 5
- Una vez obtenido el coeficiente de correlación, pueden utilizarse pruebas estadísticas y la construcción de intervalos de confianza para probar su significación.
- La significancia estadística de un coeficiente debe tenerse en cuenta conjuntamente con la relevancia clínica del fenómeno que se estudia, ya que coeficientes de 0.5 a 0.7 tienden a ser significativos en muestras pequeñas. 5
- La estimación del coeficiente de determinación (r 2) nos muestra el porcentaje de la variabilidad de los datos que se explica por la asociación entre las dos variables.
Análisis de ejemplos de la utilización del coeficiente de correlación de los rangos de Spearman en la solución de problemas de salud
Actitud ante la muerte en los médicos de familia
Los coeficientes de correlación obtenidos en la comparación de estas medidas con los promedios de la sub-escala o dimensiones del instrumento (se trabaja con el coeficiente de correlación de Spearman), por lo que se anotan los rangos numéricos de las variables sociodemográficas promediadas, y no las categorías nominales. Se busca conocer si existe relación entre estas variables y las actitudes reflejadas en las diferentes sub-escalas del CAM. Como puede deducirse del examen visual, la única correlación significativa encontrada fue entre la variable Edady la sub-escala de Temor.Esta correlación es negativa, es decir, a mayor edad de los médicos, menos es el miedo a la muerte. Esto puede explicarse porque con la edad se incrementa la experiencia profesional de contacto con la muerte, lo que actúa como un mecanismo desensibilizador. 10
Caracterización de la mujer en la etapa del climaterio
Se analiza la edad de la menarquía y de la menopausia. Para ello, se aplicó como método estadístico el coeficiente de correlación de rangos de Spearman y se encontró que no existe correlación ni dependencia entre la edad de la menarquía y la edad de la menopausia (p = 0,05 con valores críticos ± 0,31975); no se halló significación estadística. La relación entre la edad de la menopausia y el número de hijos puede verse en la Figura 2, donde se aplicó también el método estadístico del coeficiente de correlación de rangos de Spearman y en el que observamos que no existe correspondencia entre la edad de la menopausia y el número de hijos; no se encontró significación estadística (p = 0,05 con valores críticos ± 0,31975). 11
Rehabilitación multifactorial e intensiva en pacientes con esclerosis múltiple
Se analizó la relación entre el tiempo de tratamiento y la puntuación final en las escalas aplicando el test de correlación por rangos múltiples de Spearman. Las diferencias resultaron estadísticamente significativas entre las puntuaciones de las evaluaciones iniciales y finales de las escalas de Kurztke y Hauser (Z: 3,17, p=0,001475 y Z: 3,29, p=0,000983, respectivamente). No se identificó correlación entre la duración total del tratamiento ni el tiempo de evolución de la enfermedad y la puntuación final alcanzada en la escala (p< 0,05).12
CONCLUSIONES
1 La utilidad de la prueba de coeficiente de correlación de rangos de Spearman en el campo de la medicina aporta una respuesta cuantificable a la relación que en momentos determinados pueda existir entre dos variables, siendo esta un punto de partida para pronósticos y predicciones en problemas prácticos de salud.
2 El coeficiente de correlación de rangos de Spearman debe utilizarse para series de datos en los que existan valores extremos, pues si calculamos la correlación de Pearson, los resultados se verán afectados.
3 La interpretación del resultado del coeficiente de correlación de Spearman se encuentra entre los valores de -1 y 1.
4 La significancia estadística de un coeficiente debe tenerse en cuenta conjuntamente con la relevancia clínica del fenómeno que se estudia.
In the environment of the investigations epidemic clinic, the professionals of the health assiduously are projected in their investigations, to define the relationships among the characteristics of a phenomenon, the grade of that relationship or to prove the dependability of their observations, thinking about as hypothesis if these they are or it doesn't cause it of a certain entity. In the practice it generally happens that the investigator among the dissimilar statistical tests of those that prepares doesn't select appropriately the one that will contribute him a reading with more exactitude, easy of these relations. Se he carries out a bibliographical revision with the objective of characterizing the method of correlation of ranges of Spearman, used to value the association among quantitative variables, being applied the method of documental analysis. The results are declared when summarizing the history of the emergence of the theory of the correlation and the regression, explanation of associate concepts, his graphic presentation, the essential features of the algorithm of traditional solution and with advisory statistical as well as a compilation on scales of interpretation of the statistical test. He/she is projected that the carried out work serves from bibliography to consult for investigators and students of the Medical sciences.
Key words : Correlation, Spearman, Pearson, Correlation of Spearman, statistic, regression, lineal correlation, correlation coefficient, ranges, differential psychology, history .
REFERENCIAS BIBLIOGRAFICAS
1. Pita Fernández S, Pértega Díaz S. Unidad de Epidemiología Clínica y Bioestadística. Utilización e Interpretación de las Técnicas de Correlación disponible. Complexo Hospitalario Juan Canalejo. A Coruña (España):Cad Aten Primaria; 1997;4: 141-144. [Actualizado: 30/03/2001].
2. Siegel Sidney. Diseño Experimental No Paramétrico. Las medidas de correlación y sus pruebas de significación. El coeficiente de correlación de rangos de Spearman. Cuba: Edición Revolucionaria. Instituto Cubano del Libro; 1972, p. 233-245.
3. Colectivo de autores. Biografía de Charles Edward Spearman. Disponible en: http://www.biografiasyvidas/Biografia de Charles Edward Spearman.htm Barcelona,España:2004.
4. Torres Delgado JA, Quesada M. Informática médica. Asociación entre dos variables. Variables cuantitativas y coeficientes de correlación. Cuba: Editorial ECIMED; 2004;(2): 260-262.
5. Santander Montes AJ, Ruiz Vaquero R. Relación entre variables cuantitativas. Cuba:[CD].Informática Médica II. Editorial ECIMED; 2004, p.1-30.
6. Colaboradores de Wikipedia. Correlación [en línea]. Wikipedia, La enciclopedia libre, 2008 [Citado 3 abr 2008]. Disponible en: http://es.wikipedia.org/w/index.php?title=Correlaci%C3%B3n&oldid=16339013
7. Colaboradores de Wikipedia. Coeficiente de correlación de Spearman [en línea]. Wikipedia, La enciclopedia libre, 2008 [Citado 30 mar 2008]. Disponible en: < http://es.wikipedia.org/w/index.php?title=Coeficiente_de_correlaci%C3%B3n_de_Spearman&oldid=16223866.
8. Pértegas Díaz S, Pita Fernández, S. Determinación del tamaño muestral para calcular la significación del coeficiente de correlación lineal de Pearson. Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Juan Canalejo. A Coruña (España):cad aten primaria 2001;2002; 9: 209-211. Disponible en: < http://www.fisterra.com/mbe/investiga/pearson/pearson.asp > . Actualizada el 18/11/2002
9. Abraira. V, Pérez de Vargas A. Métodos Multivariantes en Bioestadística. ED. Centro de Estudios Ramón Areces. España:1996. Disponible en: < http://www.hrc.es/bioest/Reglin_1.html
10. Hernández Cabrera Gisela, González García V, Machín L, Infante Pereira O.Actitud ante la muerte en los médicos de familia. Revista Cubana Med Gen Integral. 2002;18(1):22-32. Disponible en: http://scielo.sld.cu/pdf/mgi/v18n1/mgi04102.pdf
11. Lugones Botell M, Valdés Domínguez. S, Pérez Piñero J. Caracterización de la mujer en la etapa del climaterio. Rev Cubana Obstetricia Ginecología. 2001;27(1):16-21. .Disponible en: http://scielo.sld.cu/pdf/gin/v27n1/gin03101.pdf
12. Calzada Sierra DJ, Gómez Fernández L. Rehabilitación multifactorial e intensiva en pacientes con esclerosis múltiple. Revista Neurología. 2001;32(11):1022-6. Disponible en: < http://www.revneurol.com/Web/3211/k111022.pdf
ANEXOS

Fig. 1

Fig. 2

Fig. 3
Gráfico de dispersión


Fig. 4

Fig. 5
Correlaciones

Fig.6

Fig. 7