Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
El nuevo coronavirus Sars-CoV-2, causante de la enfermedad COVID-19, presenta una rápida propagación y alto porciento de mortalidad, comparado con otros coronavirus.
Cuba se encuentra afectada por la COVID-19 y ha adoptado medidas, con el fin de contrarrestar su propagación en la población. Sin embargo, como ha sucedido en otros países afectados por esta enfermedad, se ha manifestado un crecimiento aproximadamente exponencial de casos confirmados en el país; las provincias de occidente presentan mayor número de casos que las de oriente. Entre las provincias con mayor número de casos confirmados destaca La Habana. Este comportamiento es lógico debido a que en ella se concentra aproximadamente la quinta parte de la población nacional y presenta un mayor movimiento interno y externo.
La dirección del país ha llevado a cabo medidas de gran magnitud, en coordinación con el Ministerio de Salud Pública, la Defensa Civil y otras entidades. Se han realizado pronósticos de la cantidad de personas que podrán estar en centros de confinamiento, hospitalizadas o con necesidad de cuidados intensivos, así como de personal médico disponible, entre muchas otras cuestiones. Los pronósticos de la cantidad total de personas contagiadas por provincia y el o los días de mayor número de contagios se hace imprescindible en este contexto y para realizarlo se utilizan distintas modelaciones matemáticas.
Una modelación clásica aplicada a las epidemias consiste en los modelos SIR de ecuaciones diferenciales, cuyo nombre proviene de: S (población susceptible), I (población infectada) y R (población recuperada o removida del sistema). Esta modelación tiene presente una serie de factores con el fin de expresar lo mejor posible las realidades de las epidemias y ha sido utilizada con éxitos en la epidemia provocada por la COVID-19, en algunas regiones.1,2 Sin embargo, en muchas ocasiones, presenta gran complejidad en la modelación debido a los diferentes factores a tener presente, alto nivel de procesamiento para la obtención de los modelos y alta complejidad en la interpretación de las soluciones obtenidas.
Una modelación menos compleja está basada en ajuste de modelos predictivos de crecimiento poblacional del tipo logístico y exponencial. Existen diferentes modelos que describen el crecimiento de poblaciones.3 Estos pueden ser aplicados al incremento de la cantidad de personas infectadas por una enfermedad de contagio. Entre estos modelos destacan aquellos de crecimiento logístico, de Gompertz, de Weibull. Estos han sido utilizados con éxito en la epidemia de la COVID-19 para los casos de China,4,5,6 Italia,7,8,9 Corea del Sur, Costa Rica 10 y varios países.11
El objetivo de utilizar esta modelación matemática, consiste en obtener los parámetros de los modelos que mejor se ajusten a los datos reales, para utilizar estos en predicciones futuras. Para la obtención de los parámetros, se utiliza el método de los mínimos cuadrados para modelos no lineales con respecto a los parámetros (MCNL).
Es importante seleccionar el o aquellos modelos que mejor describan la situación en estudio y presenten validez para realizar pronósticos. Debido a esto se pueden formular las siguientes interrogantes: ¿cuál o cuáles de los modelos de crecimiento poblacional aplicados se ajustan mejor a los datos reales? ¿serán adecuados el o los modelos seleccionados para realizar pronósticos futuros?
El objetivo de la presente investigación es obtener predicciones para los picos de casos confirmados y cantidad total de estos para algunas provincias de Cuba y para todo el país.
Material y métodos
El estudio predictivo realizado presenta modelos de crecimiento poblacional con adecuaciones. Fueron utilizados 7 modelos entre variaciones del modelo logístico y los modelos de crecimiento Gompertz y de Weibull. En estos, la variable dependiente está representada por los casos acumulados confirmados a la COVID-19 diariamente y la independiente por el tiempo trascurrido, luego de haberse registrado los primeros casos. La cantidad de parámetros a obtener varía entre 4 y 7 en dependencia del modelo aplicado y ha sido utilizado el método de los MCNL para su obtención. El valor de la significación a priori alfa escogido es 0,05
Los modelos utilizados en la presente investigación se exponen a continuación:
M1:
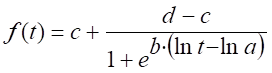. Modelo logarítmico-logístico de cuatro parámetros.12,13
M2:
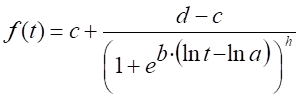. Modelo logarítmico-logístico de cinco parámetros
.(12,14)
M3:
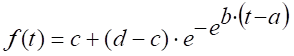. Modelo de crecimiento de Gompertz de cuatro parámetros.12,15
M4:
. Modelo de crecimiento de Weibull de cuatro parámetros.12,16
M5:
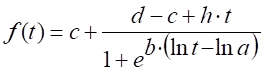. Modelo logístico de Brain and Cousens de cinco parámetros.17
M6:
. Modelo de dos fases de dosis-respuesta de siete parámetros
.(18)
M7:
, 
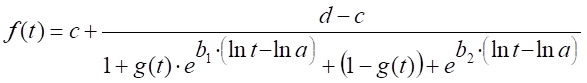. Variación del modelo logístico de cinco parámetros
.(19)
El estudio fue realizado desde mediados de marzo hasta finales de abril, en medio de la afectación de la COVID-19 en Cuba, por un grupo de profesores del Departamento de Matemáticas de la Universidad de Cienfuegos “Carlos Rafael Rodríguez”, en colaboración con el Departamento de Tecnología Educativa de este Centro.
Se estudiaron los datos reportados por Cuba referente a la cantidad de casos confirmados a la COVID-19; se comenzó el registro el 11 de marzo, fecha en la que se reportaron los primeros casos positivos de la enfermedad en el país. Los datos fueron estudiados hasta el 2 de mayo de 2020. Estos datos fueron tomados del sitio covid19cubadata.github.io, los cuales son actualizados diariamente, por colaboradores del sitio web, y compilados en un archivo de datos de extensión csv, a partir de los partes oficiales que, en conferencia de prensa, se ofrecen a todo el país.
Para el estudio, y hasta la fecha de escrito este informe de investigación (3 de mayo de 2020), se seleccionaron los 5 territorios más afectadas por la COVID-19, en función de su cantidad de habitantes. Los territorios seleccionados para el estudio fueron aquellos con tasa de infectados por cien mil habitantes mayor que 14,71, debido a que el país, en esta fecha presentaba este índice. En la tabla 1 se muestra, por provincia, la cantidad de casos confirmados y las respectivas tasas.
Tabla 1 Cantidad de casos confirmados a la COVID-19 y tasa por cada cien mil habitantes, por cada provincia y el Municipio Especial en Cuba
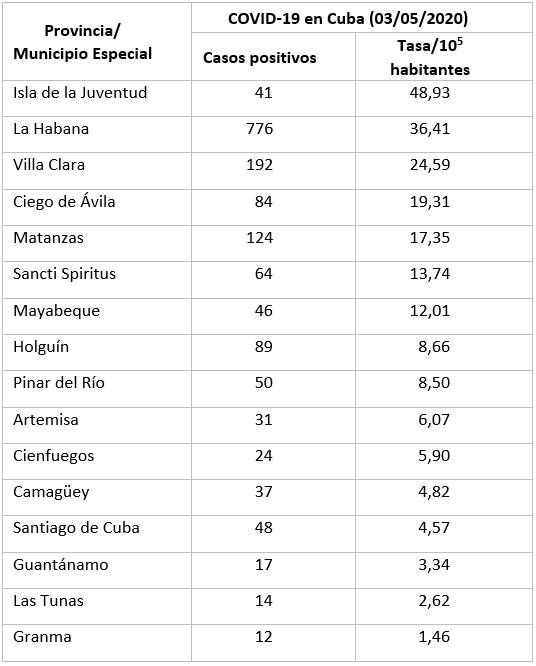
Los territorios seleccionados para el estudio fueron: Isla de la Juventud (48,93), La Habana (36,41), Villa Clara (24,59), Ciego de Ávila (19,31) y Matanzas (17,35). En la Isla de la Juventud se registraron los primeros casos el 04/04/2020; en La Habana, el 16/03/2020; en Villa Clara, el 13/03/2020; en Ciego de Ávila, el 23/03/2020 y en Matanzas, el 20/03/2020.
Las variables cuantitativas discretas, analizadas en la investigación son:
Variable independiente: Cantidad de días transcurridos desde que se confirmaron el o los primeros casos positivos a la COVID-19 por localidad y en el país.
Variable dependiente: Cantidad de casos acumulados diarios, confirmados a la COVID-19 por localidad o en el país.
Para el tratamiento de los datos y el procesamiento computacional se utilizaron scripts programados en el lenguaje de programación R 3.6.1, de procesamiento numérico.20 Los scripts pueden ser descargados desde la dirección https://clasesvirtuales.ucf.edu.cu/course/view.php?id=1147
Para el procesamiento de los modelos utilizados y la implementación del método de los MCNL se empleó la instrucción drm del paquete drc de R. Este paquete presenta herramientas para el análisis y el ajuste de modelos no lineales con respecto a sus parámetros, conocidos como modelos de dosis-respuesta, utilizados en Ciencias Médicas, Biológicas, Agropecuarias, Técnicas y Sociales. Presenta implementación de algoritmos eficientes para la obtención de los parámetros, pruebas de hipótesis para estudiar la bondad de ajuste de estos modelos y el contraste de criterios para selección del mejor o mejores modelos que se ajustan a una serie de datos. Mayor documentación puede ser encontrada en https://www.bioassay.dk.
Para el cálculo de los puntos de inflexión en los modelos M5, M6 y M7 se utilizaron métodos numéricos mediante la instrucción uniroot del paquete stat de R.
Para la selección del modelo con mejor ajuste se contrastaron varios criterios:
Coeficiente de determinación ajustado (R2), adecuado para modelos no lineales. Evalúa la efectividad que presenta la variable independiente para medir la variable dependiente.21
Criterio de información de Akaike (AIC). Expone una medida de la calidad relativa de un modelo al contrastar la bondad del ajuste con la complejidad del mismo.22
Error estándar de los residuos (RSE). Presenta una desviación media ponderada del modelo con respecto a los valores experimentales.23
Para diferentes modelos, valores del coeficiente de determinación ajustados cercanos a 1 y menores valores de AIC y de errores estándares de los residuos, ponen de manifiesto modelos con mayor adecuación.
Para verificar la bondad del ajuste, se aplicó la prueba de Neill, mediante la instrucción neill.test del paquete drc de R, adecuada para modelos no lineales con respecto a los parámetros y que utiliza técnicas de agrupamiento en caso de no contar con réplicas. 24).
Resultados
Estudio de caso de las provincias y el municipio especial Isla de la Juventud
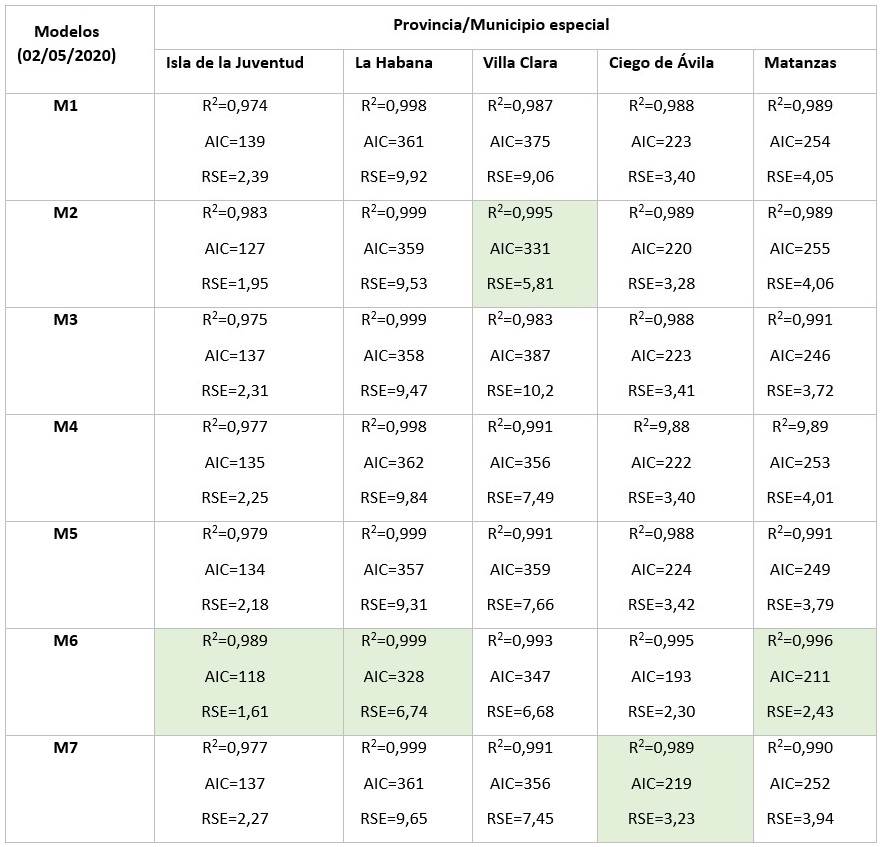
En la tabla 2 se presentan los resultados del procesamiento realizado para cada uno de los 5 territorios afectados. Se muestran los criterios de ajuste utilizados en la investigación.
Los criterios de calidad del ajuste estudiados se comportan de forma similar para cada modelo. El modelo logarítmico-logístico de cinco parámetros (M2) es seleccionado, por presentar mejores valores, en la provincia de Villa Clara, mientras que el modelo de dos fases de dosis-respuesta de siete parámetros (M6) se presenta como mejor candidato para la Isla de la Juventud, La Habana, Ciego de Ávila y Matanzas. Sin embargo, no es posible calcular predicciones, con las técnicas utilizadas en esta investigación, para el pico de la provincia Ciego de Ávila, debido a que el tiempo, al emplear el algoritmo para la búsqueda del punto de inflexión, sobrepasa la tolerancia empleada en la investigación sin haber obtenido resultado. En este caso, se selecciona el segundo modelo que proporciona los mejores índices de ajuste: M7.
La tabla 3 presenta la prueba de bondad de ajuste para cada modelo seleccionado, sus coeficientes e inferencias sobre estos y predicciones para picos de mayores contagios y cantidad total de estos, para cada uno de los territorios. Los coeficientes se nombran cuando se presentan sus valores ajustados y luego se muestran sus valores de significación al seguir el mismo orden en que se expusieron inicialmente.
Tabla 3 Coeficientes de modelos seleccionados y predicciones del día del pico de casos confirmados y total acumulado para los cinco territorios estudiados
Las pruebas de bondad de ajuste (mediante el Test de Neill), para medir la validez del ajuste, aplicadas a cada territorio con cada uno de los 7 modelos dieron valores de significación mayores de 0,05 lo que significa que ninguno de los modelos se aparta significativamente de los datos empíricos, por lo que los 7 modelos aplicados son válidos para realizar pronósticos. En la tabla 3 fueron mostrados solo los resultados correspondientes a los modelos seleccionados para cada territorio.
La figura 1 muestra la representación geométrica de los casos confirmados acumulados y los 7 modelos contrastados para la provincia de La Habana. Los modelos se ajustan de forma que se acercan entre ellos. Esto pone de manifiesto, de forma gráfica, la aproximación entre los mismos y la adecuación hacia los datos.
Fig. 1 Modelos de crecimiento poblacional ajustados a los casos confirmados acumulados en la provincia de La Habana.
Estudio de caso de Cuba
En la tabla 4 se presentan los resultados del procesamiento realizado para los casos confirmados a la COVID-19 en todo el país. Se muestran los criterios de ajuste obtenidos para cada modelo.
Los criterios de calidad del ajuste se comportan de forma similar para cada modelo. Se selecciona el modelo M6 que presenta los mejores valores.
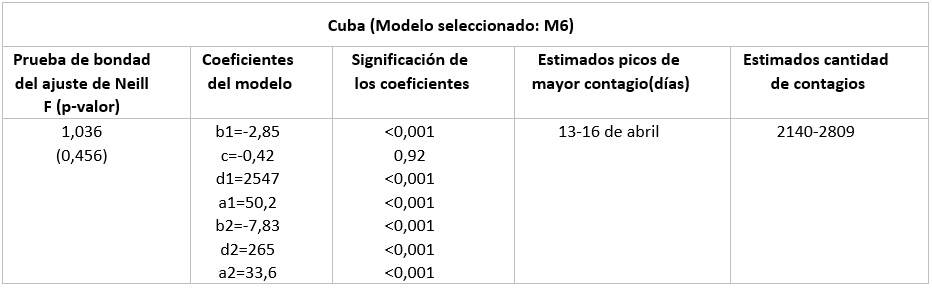
La prueba de Neill presenta niveles de significación mayores que 0,05 para cada uno de los 7 modelos aplicados a los datos de Cuba, lo cual pone de manifiesto que los modelos son adecuados para realizar pronósticos. La tabla 5 presenta los resultados de la prueba de Neill para el modelo M6, sus coeficientes ajustados y nivel de significación y predicciones para picos de mayores contagios y cantidad total de estos.
Tabla 5 Coeficientes del modelo seleccionado y predicciones del día del pico de casos confirmados y total acumulado de estos para toda Cuba
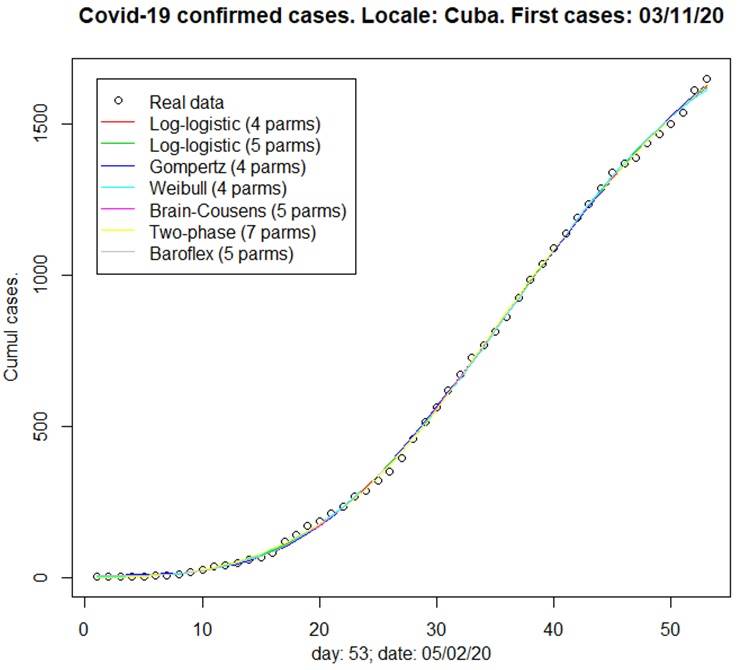
La figura 2 muestra la representación geométrica de los casos confirmados acumulados en toda Cuba y los 7 modelos contrastados. Los modelos se ajustan de forma adecuada a los datos y se aproximan entre ellos.
Discusión
En el presente estudio además de exponer predicciones para los días de mayor reporte de casos confirmados a la COVID-19 y cantidad total de estos para diferentes territorios de Cuba, se incluye a todo el país, se profundiza en la técnica utilizada para obtener dichos pronósticos. Investigaciones similares, realizadas, publicadas y revisadas por los autores han aplicado estas técnicas para obtener pronósticos sobre la epidemia provocada por la COVID-19 en otras regiones del planeta, con diferentes niveles de profundización:
Dattoli7 utiliza modelo logístico y Gompertz no aplica criterio para la selección de estos ni pruebas de significación. Jia,4 Villalobos10 y Tátrai-Várallyay11 utilizan, indistintamente, modelos logísticos, de Gompertz y Bertalanffy y un único criterio para medir el ajuste sin aplicar pruebas de significación. Prueban la adecuación de los modelos con el acertado ajuste hacia datos de epidemias ya registrados.
Yang5 contrasta modelos de crecimiento exponencial, modelos estadísticos de estimación y modelos SIR y SEIR; utiliza criterios de selección de modelos como: AIC, RSE e índice de robustez (RB); sin embargo, no presentan pruebas de significación sobre los modelos utilizados, por lo que no se conoce el nivel de confiabilidad de estos modelos, al igual que los casos anteriormente mencionados.
Batista 6 utiliza un criterio para evaluar el ajuste (R2), utiliza la prueba de significación F para probar la validez pero utiliza un único modelo: logístico.
En este estudio se utilizan 7 modelos, tres criterios para la selección del modelo de mejor ajuste y pruebas de significación, aspectos que resumen, de alguna manera, las investigaciones anteriormente mencionadas.
Los modelos utilizados en la presente investigación presentaron similares criterios sobre la calidad del ajuste y pasaron la prueba de bondad de ajuste. Esto permite su generalización para describir matemáticamente estas situaciones y pone de manifiesto la validez de cada uno para realizar pronósticos. No se puede decir basado en este estudio, que un modelo estadísticamente haya dado mejores resultados que el resto; sin embargo, se seleccionó uno de ellos para ser utilizado en cada territorio estudiado basado en los mejores valores de R2, AIC y RSE.
El modelo M6, seleccionado para la Isla de la Juventud, Matanzas y toda Cuba junto con el modelo M7 seleccionado para Ciego de Ávila, presentan el coeficiente c o c1 no significativo. Esto no invalida dichos modelos, el coeficiente c o c1 suele ser utilizado, en este contexto, como la cantidad inicial de casos al comenzar el estudio. Para el cálculo de resultados fueron tomados estos coeficientes, según los valores obtenidos al aplicar el ajuste; no obstante, debido a la función que cumplen en los modelos y que estos valores se acercan a cero, los resultados que se obtienen con estos coeficientes en cero serían muy próximos a los presentados en este estudio.
Los modelos utilizados para realizar predicciones describen correctamente los procesos de crecimientos poblacionales; aunque existen muchos factores que pueden influir en la propagación de una epidemia que en ocasiones la relación entre dos variables (dependiente e independiente) no puede expresar.
La técnica utilizada está basada en las observaciones ya existentes y la obtención a partir de ellas de los parámetros de modelos ya preestablecidos. Mientras mayor sea el número de observación, mejor aproximación se obtendrá de los mismos; sin embargo, mayor tiempo habrá transcurrido de afectación de la epidemia.
Jia4 ha realizado pronósticos satisfactorios, pasados aproximadamente 40 días luego de los primeros reportes y Villalobos 10 pasados 50 días. Los territorios analizados en esta investigación se encuentran pasados 40 días de haberse registrado los primeros casos a excepción de la Isla de la Juventud donde han transcurrido 29 días. Cuba se encuentra pasados 53 días.
Conclusiones
Los modelos de crecimiento poblacional para la obtención de pronósticos de días de mayor afectación y cantidad total de contagios, por la COVID-19 en territorios de Cuba y en todo el país, han sido probados estadísticamente y dan resultados significativos. Los mismos presentan validez y criterios de ajuste similares por lo que se puede concluir que todos los modelos utilizados en el estudio presentan adecuación para realizar pronósticos.
En la presente investigación se obtuvieron predicciones al utilizar los modelos M2, M6 y M7, luego de probar la validez del ajuste mediante prueba de bondad de ajuste y de significación sobre sus coeficientes. De esta forma se evidencia la confiabilidad en las predicciones presentadas.
