Introducción
El tema de las paradojas en la Matemática en el proceso de enseñanza - aprendizaje, ha sido tratado en varios trabajos, entre ellos (Talero, Santana, & Mora, 2015) los cuales, a partir de la interpretación gráfica del movimiento uniforme rectilíneo y la serie geométrica, aclaran la popular paradoja de Aquiles y la tortuga. En la Física, este resultado se puede usar como ejemplo en cursos elementales de cálculo y mecánica. En el trabajo de (Tasenm, 2010) se relata brevemente la historia de las Paradojas Matemáticas y los primeros matemáticos que comenzaron a estudiar este tema desde el punto de vista de la lógica matemática. (Macho, 2012) hace un recorrido por varios ejemplos concretos de paradojas de diferentes tipos, como desapariciones geométricas, anamorfosis, paradojas lógicas, del infinito, de la vaguedad, entre otras.
En (Martínez, 1999) se presenta una secuencia de razonamiento matemático basado en la resolución de una paradoja, con la intención de que dicha propuesta se utilice en los cursos de formación de profesores de matemáticas de secundaria. El autor plantea que mediante la realización de módulos formativos basados en la búsqueda de significado y de resolución de paradojas, se puede poner a los profesores en formación a hacer matemáticas con problemas elementales, idea que luego hará llegar a sus estudiantes.
Más información sobre la teoría y aplicaciones de las Paradojas Matemáticas se puede consultar en (Acharya, Basu, & Das, 2015), (Castro & Hernando, 2003) y (Chaitin, 2003).
En la actualidad, uno de los mayores problemas que enfrentan las ciencias académicas en todo el mundo es la falta de motivación de los estudiantes hacia las mismas, lo que va aparejado con el poco interés en su estudio y la no participación en las clases. El caso más grave y preocupante es el de la Matemática, un problema del cual pocas personas están ajenas. Cuba no está exenta de esta situación, y es siempre una meta lograr que en las aulas los estudiantes se motiven a estudiar algo que no les gusta, y, por tanto, muchas veces se trata de lograr primero que les guste. En este sentido, en este trabajo los autores se proponen como objetivo abordar el tema de las Paradojas Matemáticas, proponiendo las mismas como una herramienta más que les sirva de apoyo a los profesores en la misión de motivar a los estudiantes, tomando como problema fundamental, la desmotivación de los estudiantes hacia esta ciencia. Además, se proponen las paradojas como vía para generar situaciones problémicas que posibiliten el debate y la generación de ideas entre los estudiantes. Por otro lado, se presentan los resultados de los experimentos desarrollados en varios grupos de diferentes niveles de enseñanza en varias escuelas.
Desarrollo
Se presentan algunas definiciones y tipos de paradojas, que ayudarán al lector a comprender mejor. Luego se presentarán algunos ejemplos prácticos de paradojas y se verán las soluciones de algunas. Es interesante hacer notar que existen bastante tipo de paradojas, así como definiciones de éstas, por tanto, los autores no pretenden ser exhaustivos.
Tipos de paradojas
El término “paradoja” puede interpretarse como algo que a primera vista parece ser falso pero que en realidad es cierto, o que parece ser cierto pero que en rigor es falso, o sencillamente que encierra en sí mismo contradicciones. El término paradoja se origina en el latín paradoxus, que a su vez proviene del griego paradoxos ―παράδοξος―. Etimológicamente, paradoxos significa lo que parà ten doxan, “lo que va en contra de la opinión pública” (Tasenm, 2010). Según (Muñoz, 2007) las paradojas se pueden clasificar de la siguiente forma:
Según su veracidad: En el primer grupo, se pueden encontrar paradojas que solo parecen serlo (lo que afirman es realmente cierto o falso), otras se contradicen, mientras que otras dependen de su interpretación para ser o no paradójicas.
Son resultados que aparentan tal vez ser absurdos a pesar de ser demostrable su veracidad. A esta categoría pertenecen la mayor parte de las paradojas matemáticas.
Paradoja del cumpleaños: ¿cuál es la probabilidad de que dos personas en una reunión cumplan años el mismo día?
Paradoja de Galileo: a pesar de que no todos los números son números cuadrados, no hay más números que números cuadrados.
Paradoja del hotel infinito: un hotel de infinitas habitaciones puede aceptar más huéspedes, incluso si está lleno.
Son paradojas que alcanzan un resultado que se autocontradice, aplicando correctamente modos aceptados de razonamiento. Muestran fallos en un modo de razón, axioma o definición previamente aceptados. Por ejemplo, la Paradoja de Grelling-Nelson señala problemas genuinos en nuestro modo de entender las ideas de verdad y descripción. Muchos de ellos son casos específicos, o adaptaciones, de la Paradoja de Russell.
Paradoja de Russell: ¿Existe un conjunto de todos los conjuntos que no se contienen a sí mismos?
Paradoja de Curry: “Si no me equivoco, el mundo se acabará en diez días”
Paradoja del mentiroso: "Esta oración es falsa"
Paradoja de Grelling-Nelson: ¿Es la palabra "heterológico", que significa “que no describe a sí mismo”, heterológica?
Estas paradojas se basan en definiciones ambiguas, sin las cuales no alcanzan una contradicción.
Paradoja sorites: ¿En qué momento un montón deja de serlo cuando se quitan granos de arena?
Paradoja de Teseo: Cuando se han reemplazado todas las partes de un barco, ¿sigue siendo el mismo barco? (pp. 4-6)
Otro grupo importante de paradojas son las lógico - matemática. Estas son tomadas en muchos casos como el faro guía de las demás definiciones. Constituyen un grupo importante y son las que más han aportado a los fundamentos de la Matemática. Entre ellas se encuentra la paradoja de Banach-Tarski o de Hausdorff, la cual, en un lenguaje no formal, afirma que es posible fabricar un rompecabezas tridimensional de un total de ocho piezas, las cuales, combinadas de una determinada manera, formarían una esfera completa y rellena (sin agujeros) y, combinadas de otra manera, formarían dos esferas rellenas (sin agujeros) del mismo radio que la primera (Muñoz, 2007). Esta paradoja tiene un fundamento puramente matemático. Pertenece a la Topología y aunque no lo parezca, más que una paradoja, es un teorema con interesantes consecuencias en el área.
Hay otras paradojas cuyo centro está en el concepto de infinito como la de Galileo: a pesar de que no todos los números son números cuadrados, no hay más números que números cuadrados. Se refiere a los números los naturales (o enteros). Afirma que el conjunto de los números naturales (o enteros) tiene la misma cantidad de elementos que el conjunto del cuadrado de sus elementos, aunque pareciera que este último tiene menos números por ser subconjunto del anterior. También están las tres paradojas de Zenón sobre el movimiento: a) la de Aquiles y la Tortuga, la cual afirma que el primero nunca puede alcanzar a la tortuga; b) la del lanzamiento de la flecha, afirma que la flecha nunca se mueve, en cada instante siempre está en reposo; c) por último la paradoja que afirma la imposibilidad de moverse de un punto A otro punto B.
Existen muchos otros tipos de paradojas, entre ellos, Muñoz (2007) también destaca:
Paradojas sobre Lógica: A pesar de que todas las paradojas se consideran relacionadas con la lógica, hay algunas que afectan directamente a sus bases y postulados tradicionales. Las paradojas más importantes relacionadas directamente con el área de la lógica son las antinomias, como la paradoja de Russell, que muestran la inconsistencia de las matemáticas tradicionales. A pesar de ello, existen paradojas que no se contradicen y que han ayudado a avanzar en conceptos como demostración y verdad.
Paradoja del rey de Francia: ¿es cierta una afirmación sobre algo que no existe?
Paradoja del cuervo (o cuervos de Hempel): una manzana roja incrementa la probabilidad de que todos los cuervos sean negros. (p. 7)
Ejemplos de paradojas y su tratamiento metodológico
Las primeras paradojas serán sobre demostraciones falsas, las últimas serán geométricas. Se propondrá metodológicamente cómo los profesores pueden tratar este tema con los estudiantes. Comenzaremos con la demostración de que “2 = 1”, el razonamiento es el siguiente:
Comencemos por plantear que, a = b,
Multiplicando por a ambos miembros se tiene, a 2 = ab,
Restando b 2 , a 2 - b 2 = ab - b 2 ,
Factorizando, (a + b) (a - b) = b(a - b),
Simplificando a - b, a + b = b,
Haciendo a = b (la suposición inicial) se tiene, 2b = b,
Y finalmente simplificando b, se llega a, 2 = 1.
Ahora, el principal problema está en que se sabe que el resultado final es falso, pero la idea entonces es ¿dónde está el error en el procedimiento? ¿Qué se hizo mal? Al parecer nada, todos los pasos parecen correctos. En este punto es necesario motivar al estudiante a que busque dónde pudo haber fallado el procedimiento, de lo contrario estará aceptando que 2 = 1, lo cual no parece ser tan falso ahora, en particular esto implica que todos los números son iguales, y la demostración se podría dejar de estudio independiente. El error está en simplificar a - b, en el 5to paso, ya que se partió de que a = b, por tanto, a - b = 0, lo que quiere decir que se dividió por cero, lo cual no es posible y por eso se llegó al error.
Otra interesante demostración es la de que 1 es menor que 0 (1 < 0):
Comenzamos por plantear que, 0.5 < 1, lo cual es verdadero,
Aplicamos logaritmo en base 10 a ambos miembros, log 0.5 < log 1,
Dividiendo por log 0.5 ambos miembros y simplificando se tiene,
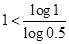 ,
,
Como log 1 = 0, sustituyendo se tiene,
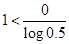 ,
,
Lo cual es equivalente a, 1 < 0.
Nuevamente se llega a las preguntas de antes, haciendo transformaciones aparentemente correctas, se llega a un resultado, que, según la intuición, debería ser falso. Estos son ejemplos donde se refleja que no solo basta con realizar pasos que parecen correctos, sino que el estudiante debe entender que, en lo cotidiano, realmente se debe verificar si realmente los pasos son correctos analizando los detalles. Todas las reglas que se han usado han sido correctas, y se partió de algo verdadero, dónde puede estar el error. Éstos son los momentos de situación problémica que se debe aprovechar para que los estudiantes participen, incluso el más atrasado sabe que hay un problema el cual entiende, que 1 no puede ser menor que 0, sin embargo, él mismo no sabe por qué sucede eso, situación que lo motiva a, por lo menos, pensar dentro de sí en buscar una solución.
Finalmente, después de una minuciosa búsqueda, se puede apreciar que el error en estos procedimientos está en la división por log 0.5, ya que es un número negativo, log 0.5 ≈ -0.301, y, por tanto, al dividir, se debe cambiar el signo de <, a >, lo cual no se hizo, pues log 0.5 oculta que el signo sea negativo. Esta situación es común en muchas paradojas, el hecho de que la solución no es complicada, sino que, está oculta y lo complicado es encontrarla.
Estas soluciones sencillas como cambiar el signo de una desigualdad, o la división por cero, no dejan de ser educativas en sí mismas, ya que le recuerda al estudiante que debe tener cuidado en sus cálculos y en los procedimientos que realice, para no cometer errores como estos. Finalmente se expondrán dos interesantes paradojas geométricas, cuyas soluciones no serán explicadas por motivos de espacio.
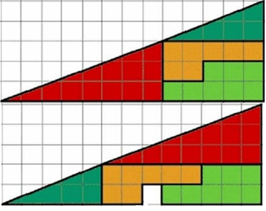
La primera paradoja se presenta más abajo en la figura 1. La primera imagen presenta un triángulo dividido en partes, en la segunda, estas partes son reordenadas en la misma ubicación del área que ocupa el triángulo original. Como resultado, se tiene que las piezas ocupan el mismo espacio, sin embargo, se puede notar que ha desaparecido un cuadradito de los que conforma el triángulo, o sea, se ha perdido área. Esto no debe pasar, ya que las mismas piezas que se cortaron, solo se reordenaron, así que deberían formar el mismo triángulo, pero no es así.
Figura 1. Primera paradoja geométrica
Fuente: (Macho, 2012)
Esta paradoja es curiosa y contradice el sentido común, es una de las que más efecto tiene en el debate de los estudiantes en las clases de Geometría. Muy similar, es la siguiente, cuya solución se basa en el mismo principio que la antes expuesta. Se puede apreciar en la figura 2.
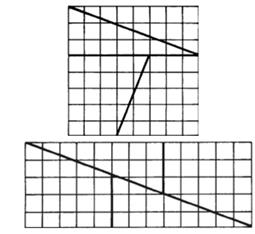
Figura 2. Segunda paradoja geométrica
Fuente: (Macho, 2012)
El primer cuadrado de la figura 2 es de 8x8 casillas, o sea, 64. Este cuadrado está cortado en 4 partes, las cuales son reordenadas, al igual que la paradoja de la figura 1, para formar el rectángulo de abajo. El problema está en que este rectángulo es de 5x13, lo que equivale a 65 casillas, una más que el cuadrado que forman las piezas originalmente, lo cual no debería pasar.
Estos son algunos ejemplos de paradojas que pueden ser tratados en clases y cuya solución el estudiante puede comprender sin conocimientos avanzados en Matemática. Existen muchas otras, como demostrar que 1 = - 1, otra de que 2 = 1, etc., las cuales, pueden cumplir el mismo objetivo de asombrar y generar debate participativo de los estudiantes en las clases. Este debate es interesante, ya que el estudiante se ve en la necesidad de pensar, pero no es un pensamiento obligado, sino que, motivado por él mismo, su creencia de que tales situaciones no se pueden dar y la necesidad de buscarles una solución. Este proceso logra que el estudiante active el cerebro, algo que con los estudios independientes y clases prácticas se desea lograr, pero que muchas veces no se alcanza.
Por ejemplo, las actividades como resolver integrales definidas o indefinidas, calcular derivadas, valores y vectores propios, hacer demostraciones teóricas, ejercicios de Geometría, entre otros, ponen al estudiante en la situación de que tiene que resolverlos porque va a ser evaluado, y tiene que adquirir esos conocimientos. Sin embargo, en una paradoja, aunque no se le oriente que la resuelva, él mismo entra en el conflicto de que algo está contradiciendo su sentido común y lo que hasta ahora conocía como verdadero, y no sabe por qué, ya ese es un motivo para que comience a intentar buscar la respuesta. Un punto interesante es que muchas veces es más difícil ver la solución de una paradoja, que resolver los ejercicios de clase.
Los autores creen que las Paradojas Matemáticas, debido a sus características, constituyen una fuente para lograr asombro, curiosidad y motivación en los estudiantes hacia las asignaturas de esta ciencia. Las mismas, abren el camino al interés por el estudio y la búsqueda de información. Si son bien utilizadas en el proceso de enseñanza - aprendizaje, se puede lograr además que los estudiantes alcancen una cultura matemática general integral.
Experimento y resultados
El experimento desarrollado en la investigación durante dos años (desde septiembre de 2017 a mayo de 2019) en Guantánamo, se aplicó a varias escuelas, como la Secundaria Básica “Celia Sánchez Manduley” en Bayate Arriba, El Salvador, la “Manuel Ascunce Domenech” del municipio Guantánamo, el IPVCE “José M. Maceo Grajales”, algunos grupos de 2do y 3er año de la carrera de Economía, Contabilidad, Informática, Industrial y Matemática de la Universidad de Guantánamo. En general, se experimentó con un total de 310 estudiantes.
El experimento consistió en, primeramente, observar la opinión y la actitud de los estudiantes en las clases, haciéndoles preguntas orales y escritas, conversando con ellos. La principal idea es hacerlo sin que ellos noten que están siendo evaluados, para que no reflejen un criterio parcial de forma intencionada a favor o en contra de las asignaturas de Matemática. Luego de saber el criterio general de los estudiantes, la segunda fase es incluir en las clases algunos temas relacionados con las Paradojas Matemáticas, en busca de motivación (esto es realizado nuevamente con discreción, como algo natural en las clases para que los resultados sean imparciales). La tercera parte y final, es comparar el criterio inicial de los estudiantes, con los obtenidos luego de hablarle sobre varias paradojas.
Como resultado, inicialmente, el 30% (93 estudiantes) del total estaban motivados, luego de los experimentos, cerca del 63.87% (198 estudiantes) mostraron más interés y motivación en las clases, lo que corresponde a las 93 iniciales más otros 105 estudiantes. El restante 36.13% de los estudiantes mostraba desinterés por diversas razones. Por otro lado, se observó que, cuando se plantean como una situación problémica, casi todos los estudiantes participan en la búsqueda de la solución para intentar resolver la situación. Aunque esta primera prueba por dos años no mostró un 100% de aprobación como se hubiese deseado, sí mostró efectividad, y deja claro que poco a poco, haciendo un trabajo continuo en el proceso de enseñanza - aprendizaje desde las primeras enseñanzas, con esta y otras herramientas, se puede lograr que los estudiantes de modo general, acepten un poco más esta ciencia.
En el caso de la medición del criterio sobre la motivación de los estudiantes, en la primera y segunda fase, los autores decidieron hacerlo de esta manera, precisamente para buscar una opinión lo más natural posible. Con métodos como una encuesta y otros que reflejen numéricamente el estado de opinión, los estudiantes se involucrarían demasiado, y entrarían otros factores a incidir en el resultado final, y precisamente, es lo que no se quiere.
Conclusiones
Las paradojas forman parte del mundo matemático y han contribuido al desarrollo de esta ciencia, son fuente de motivación y curiosidad. Este aspecto es interesante usarlo en el proceso de enseñanza - aprendizaje, con el objetivo de buscar motivación en los estudiantes.
En este trabajo, se desarrollaron algunas paradojas, para que sirvan de iniciación y base a los profesores en sus clases. Además, se mostraron los resultados de la investigación desarrollada por los autores durante dos años, donde se refleja la efectividad de incluir temas relacionados con las Paradojas Matemáticas en las clases en búsqueda de motivación y participación.
En futuras investigaciones es interesante seguir abordando otros temas relacionados con las paradojas que aparecen en cada una de las asignaturas de Matemática, y establecer estrategias de enseñanza - aprendizaje para incluir dichas paradojas de forma natural en las clases, dejando tareas, situaciones problémicas de debate, entre otros, sin que esto constituya atraso o desviación en los contenidos del programa de la asignatura, sino que, los complemente.