Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.33 no.1 La Habana ene.-abr. 2012
APLICACIONES INDUSTRIALES
Barrido de frecuencia en coordenadas de fase
Frequency scan on phase-coordinates
Dr. Ignacio Pérez AbrilI, MSc. Jandecy Cabral LeiteII
ICentro de Estudios Electroenergéticos. Universidad Central "Marta Abreu" de Las Villas. Cuba.
IIInstituto de Tecnología y Educación de la Amazonía ITEGAM. Brasil.
RESUMEN
El análisis de redes eléctricas ha transitado de modelos en componentes de secuencia a modelos en coordenadas de fase. La formulación del barrido de frecuencia en coordenadas de fase, además de facilitar la modelación más precisa de las redes desequilibradas, permite especificar inyecciones armónicas de cualquier tipo: monofásicas o trifásicas de la secuencia deseada. Por lo que puede estudiarse el efecto de las cargas no lineales de acuerdo a sus características y conexión al circuito. El presente trabajo desarrolla el modelo en coordenadas de fase de una red eléctrica, considerando la representación de bancos de transformadores monofásicos de tres o dos transformadores, así como otros tipos de asimetrías que pueden encontrarse en los sistemas eléctricos de instalaciones industriales, de edificios comerciales o de servicio. El modelo desarrollado se prueba con un ejemplo sencillo de un sistema delta a cuatro hilos que permite destacar las posibilidades del modelo.
Palabras clave: análisis de armónicos, barrido de frecuencia, coordenadas de fase.
ABSTRACT
The electric networks analysis has upgraded from the sequence components frame models to the phase- coordinates frame models. The formulation of the frequency scan method in a phase- coordinates frame, besides allowing for a more accurate modeling of unbalanced networks, allows the specification of harmonic injections of any type: single-phase or three-phase of the desired sequence. Therefore, it is possible to study the effect of the non-linear loads according to its features and connection to the circuit. This paper develops the phase-coordinates model of a distribution power system, considering the representation of three-phase transformer banks of three or two single-phase transformers, as well as other asymmetries that can be found in the electrical systems of industrial plants, commercial or service facilities. The frequency scan based on the presented model is tested with a simple example of a four-wire delta system that highlights the possibilities of the model.
Keywords: harmonic analysis, frequency scan, phase-coordinates.
INTRODUCCIÓN
El análisis de redes eléctricas desequilibradas ha transitado de la utilización de modelos en componentes de secuencia a modelos en coordenadas de fase [1-2].
Tanto en las redes eléctricas de instalaciones industriales, como en las de instalaciones comerciales o de servicio, aparecen situaciones que ameritan el uso de modelos de este tipo, como son:
a) Empleo de bancos de transformadores asimétricos, compuestos por transformadores de capacidad diferente e incluso bancos abiertos y que utilizan conexiones asimétricas (delta a cuatro hilos, etc.)
b) Empleo de alimentadores de cuatro, tres y dos hilos, trifásicos y monofásicos.
c) Empleo de cargas monofásicas conectadas entre fases o entre fase y neutro.
Estos modelos pueden emplearse para analizar el comportamiento de la red tanto a frecuencia fundamental como a otras frecuencias, y pueden ser empleados para el análisis de armónicos en este tipo de redes desequilibradas.
Dentro de las técnicas empleadas para el análisis de armónicos, el barrido de frecuencia ocupa un lugar especial por su empleo en la detección de posibles resonancias en la red, lo que la convierte en una herramienta muy empleada para el diseño de filtros de armónicos [3-4].
La formulación en coordenadas de fase de este método, además de facilitar la modelación más precisa de las redes desequilibradas, permite especificar inyecciones de armónicos de cualquier tipo: monofásicas o trifásicas de la secuencia deseada. Por lo que puede estudiarse el efecto de las cargas no lineales de acuerdo a sus características y conexión al circuito.
Diferentes publicaciones han tratado la modelación trifásica de la red [1-3, 5, 6]. No obstante, la presencia de asimetrías importantes en la red hace necesario incorporar nuevos modelos en coordenadas de fase para representar los bancos de transformadores monofásicos de tres o dos transformadores en sus distintas conexiones [7-10]. Se ha utilizado un barrido de frecuencia en coordenadas de fase para analizar sistemas en conexión estrella [11-13], no obstante, no se han analizado los sistemas delta de cuatro hilos que son muy empleados en la distribución secundaria.
El presente trabajo desarrolla el modelo en coordenadas de fase de una red eléctrica desequilibrada, considerando la representación de bancos de transformadores monofásicos de tres o dos transformadores, así como otros tipos de asimetrías que pueden encontrarse en los sistemas eléctricos de instalaciones industriales, de edificios comerciales o de servicio.
El modelo desarrollado se prueba con un ejemplo sencillo de un sistema delta a cuatro hilos que permite destacar las posibilidades del modelo en coordenadas de fase.
BARRIDO DE FRECUENCIA
El barrido de frecuencia es la técnica más sencilla y comúnmente empleada para el análisis de armónicos y presenta los mínimos requerimientos de datos [3-4]. En esencia, el barrido de frecuencia determina la respuesta de frecuencia de una red vista desde un nodo particular de la misma.
Típicamente, se inyecta una corriente de 1 pu de una frecuencia dada en el nodo de interés y se calcula la tensión que aparece en dicho nodo. Este cálculo se repite para el rango de frecuencias que se estudia utilizando un incremento determinado para los pasos de frecuencia empleados.
El proceso se basa en resolver le expresión matricial:
![]()
Donde U(f), Z(f) e I(f), son el vector de tensiones, la matriz impedancia y el vector de las inyecciones de corriente para cada frecuencia f.
En un estudio típico, solo el elemento k del vector I(f) tiene valor unitario, mientras el resto es cero. De forma que el vector U(f) resultante se correspondería con la columna k de la matriz impedancia para dicha frecuencia.
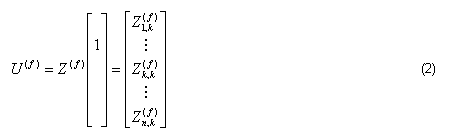
El elemento Uk(f) es la tensión de frecuencia f que se produce en el nodo k cuando se inyecta una corriente unitaria de dicha frecuencia en dicho nodo. En otras palabras, se corresponde con la impedancia equivalente de Thevenin del nodo k, Zk,k(f).
Cada elemento Um(f) con m ≠ k, representa la tensión de frecuencia f que aparece en el nodo m por una inyección en el nodo k. Es decir, se corresponde con la impedancia transferencial Zm,k(f).
Concluido el procedimiento se obtienen las características contra frecuencia de la impedancia equivalente y las impedancias transferenciales.
Este tipo de estudio es la herramienta más efectiva para detectar resonancias en el sistema y ha sido ampliamente utilizada para el diseño de filtros.
La matriz impedancia de la red para cada frecuencia se determina como la inversa de la matriz admitancia Y(f) que se construye a partir de los modelos establecidos para los diferentes elementos del sistema eléctrico [3-4].
Utilizado el modelo del sistema para secuencia positiva, negativa o cero, pueden obtenerse las características de impedancia contra frecuencia para inyecciones de las distintas secuencias, lo que permite ampliar las posibilidades del estudio y su aplicación a sistemas desequilibrados.
Sin embargo, algunos tipos de redes eléctricas de distribución, sistemas eléctricos industriales o instalaciones comerciales y de servicio, son tan desequilibrados que en este tipo de redes puede lograrse una modelación más efectiva empleando modelos en coordenadas de fase en contraposición a los tradicionales modelos en componentes de secuencia.
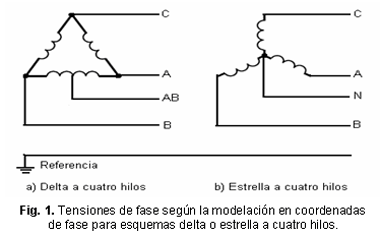
En esencia, la modelación en coordenadas de fase es capaz de determinar la tensión en todos los puntos o nodos de interés con respecto a un nodo de referencia que en general es la tierra, pero que en el caso de un sistema no aterrado, o asimétrico como el sistema delta de cuatro hilos, es un nodo ficticio de referencia. Figura 1.
El barrido de frecuencia en coordenadas de fase, a diferencia de su variante en componentes de secuencia, no puede inyectar corriente en un solo nodo (fase) de la red, ya que es preciso especificar el nodo (fase) de retorno para dicha inyección. Esta aparente dificultad es una ventaja del método, ya que permite especificar inyecciones de cualquier tipo: monofásicas o trifásicas de la secuencia deseada. Por lo que puede estudiarse el efecto de las cargas no lineales de acuerdo a sus características y su conexión al circuito.
Si ahora U(f), Z(f) e I(f), son el vector de tensiones, la matriz impedancia y el vector de las inyecciones de corriente para cada frecuencia f en coordenadas de fase. La determinación de las tensiones de fase para estímulos diversos se realiza de la siguiente manera:
Una inyección monofásica entre los nodos k y m (retorno) se representa mediante una corriente de +1 pu en el nodo k y de -1 pu en el nodo m, obteniendo el siguiente resultado.
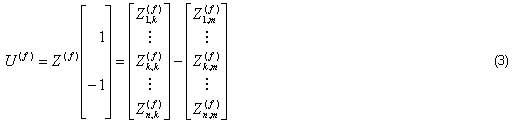
Por su parte, una inyección trifásica de secuencia positiva en los nodos k, m y t se calcularía mediante:
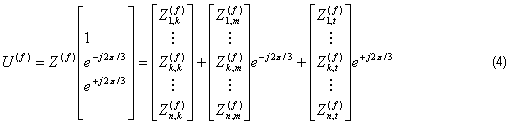
Como se ve, cualquier tipo de inyección: monofásica, bifásica o trifásica puede representarse en este tipo de modelación de la red, lo que le da una gran versatilidad al barrido de frecuencia.
Una vez obtenidas las tensiones de fase con respecto al nodo de referencia, pueden determinarse las tensiones de fase a fase mediante la diferencia entre las tensiones de fase calculadas.
IMPLEMENTACIÓN
Para implementar el barrido de frecuencia en coordenadas de fase, se ha considerado una modelación capaz de representar la red con un grado de detalle considerable. Cada fase (A, B, C), derivación central entre dos fases (AB, BC, CA) o neutro de la conexión estrella se representan por nodos independientes. Todos los nodos declarados en la lista de nodos son permanentes y nunca se eliminan, a diferencia de los neutros flotantes que se crean cuando se declara un elemento en conexión estrella, los que se eliminan en el proceso de formación del modelo.
La base del método radica en la formación de la matriz admitancia de la red para cada frecuencia, la que se compone adicionando las submatrices admitancia de los diferentes elementos que integran el sistema eléctrico: transformadores, alimentadores, máquinas y otros elementos pasivos como bancos de condensadores, etc.
TRANSFORMADORES
El modelo de los transformadores trifásicos y de los bancos de transformadores monofásicos es una de las partes más complicadas del modelo de la red, por la diversidad de conexiones y configuraciones posibles.
No obstante, este problema puede simplificarse si se representa cada transformador trifásico como un banco de tres transformadores monofásicos y se realiza el análisis por separado a cada una de las unidades monofásicas componentes de los bancos de transformadores [7-9].
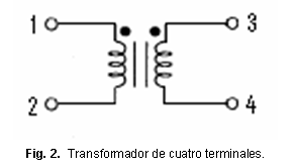
Se consideran los casos de transformador monofásico con cuatro y cinco terminales. Ver figura 2.
Si se introduce h como la relación de la frecuencia f a la nominal, la admitancia serie del transformador a la frecuencia f es:
![]()
En el cálculo de y puede considerarse el efecto pelicular añadiendo una resistencia de valor 80X en paralelo a la reactancia [3-4].
Si α y β representan las posiciones de las derivaciones por primario y secundario, la matriz admitancia del transformador monofásico con cuatro terminales es:
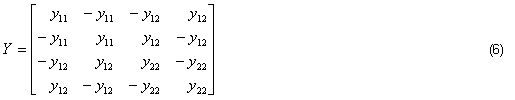
Donde:
![]()
Debe aclararse, que en caso de que el devanado primario o secundario esté conectado de fase a fase (conexión delta), la derivación correspondiente, α o β se multiplica por √3.
Los nodos 1 y 3 son siempre una fase, mientras que los nodos 2 y 4, pueden ser una segunda fase (conexión delta) o un neutro (conexión Y). En caso de que un neutro esté conectado directamente al nodo de referencia, se extraen la fila y la columna correspondientes de la matriz.
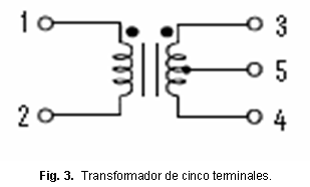
Un transformador con derivación central en el secundario tiene cinco terminales. Ver figura 3.
La matriz admitancia de este tipo de transformador es:
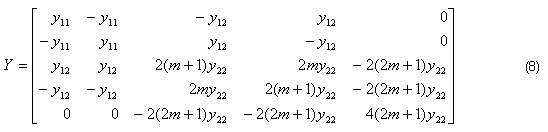
Donde m es la relación entre la impedancia del primario y del secundario del transformador [10].
En este caso, el nodo 4 siempre es una segunda fase, y el 5 es el neutro por secundario de un sistema delta a cuatro hilos. No obstante, el nodo 5 nunca puede eliminarse, pues en la modelación realizada, no está conectado al nodo de referencia, por lo que tiene que tratarse como una fase más.
La matriz admitancia del banco de transformadores se forma por la superposición de la submatriz de cada transformador que lo compone.
Una vez que se obtiene la matriz admitancia del banco, los nodos que representan el neutro de los devanados en conexión Y no aterrada, pueden eliminarse por álgebra de matrices, dado que la corriente es cero por el neutro en este caso.
En el modelo en coordenadas de fase, los desfasajes que se producen entre primario y secundario, debido a las conexiones de los transformadores, se determinan de forma natural y no tienen que especificarse, lo que si es necesario considerar en los modelos en componentes de secuencia.
ALIMENTADORES
La representación de los alimentadores se realiza por el circuito Π para líneas cortas y empleando la formulación habitualmente utilizada en programas de este tipo [3].
La autoimpedancia Zaa de un conductor a con retorno por tierra y la impedancia mutua Zab entre los conductores a y b, se calculan mediante [10]:
![]()
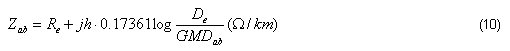
Re y De son la resistencia y la profundidad del conductor de Carson, ambos dependientes de la frecuencia, mientras que Ra y GMRa son la resistencia y el radio medio geométrico del conductor a. GMDab es la distancia media geométrica entre los conductores a y b. Existen expresiones para considerar el crecimiento de Ra por efecto pelicular [3-4].
Calculadas las impedancias serie de los conductores para la frecuencia deseada, se forma la matriz de impedancias de la línea (cable) en dependencia del número de conductores (fases) que posea.
Por ejemplo, una línea trifásica con neutro se representaría por:

Si el conductor neutro enlaza nodos que se han eliminado, la caída de tensión en dicho conductor se adiciona a la de las fases para obtener las tensiones con respecto a neutro. Esto se hace eliminando la fila y columna correspondiente mediante álgebra de matrices.
Con respecto a la susceptancia capacitiva de los cables, se utilizan los valores tabulados para distintos tipos de cables en función de su tensión y sección, que se ofrecen en [14], etc.
Siguiendo este procedimiento, se consigue una representación de la matriz admitancia del alimentador en coordenadas de fase que se describe por:

Donde Yp y Zs, son submatrices que representan la susceptancia capacitiva y la impedancia serie de la línea.
MÁQUINAS ROTATORIAS
En las máquinas sincrónicas y de inducción, el campo magnético giratorio creado por los armónicos del
estator gira a una velocidad significativamente superior a la del rotor, lo que provoca que la impedancia a frecuencias armónicas se aproxime a la impedancia de secuencia negativa de la máquina [3-4].
En el caso de las máquinas sincrónicas, se utiliza la reactancia de secuencia negativa o el promedio de las reactancias subtransitorias de eje directo y cuadrático calculadas para la frecuencia deseada.
![]()
Las máquinas de inducción se representan comúnmente por su circuito equivalente a rotor bloqueado, cuyos parámetros se actualizan a la frecuencia deseada.
En ambos casos, la dependencia de la resistencia con la frecuencia puede ser significativa debido al efecto pelicular y el incremento de las pérdidas por corrientes parásitas [3-4]:
Una vez que se dispone de la admitancia serie de la máquina y, la matriz admitancia de una máquina en conexión delta es:

CARGAS PASIVAS
Las cargas pasivas lineales tienen un efecto significativo en la respuesta de frecuencia del sistema, principalmente en la cercanía de las condiciones de resonancia.
Los modelos más generalmente empleados en la bibliografía [3-4] para este tipo de cargas son el modelo paralelo y el modelo serie.
El modelo paralelo representa la carga por una resistencia y reactancia en paralelo. Este es el modelo más amortiguador debido a la presencia de la resistencia en paralelo, por lo que su empleo conduce a los resultados más optimistas.
![]()
El modelo serie utiliza una impedancia serie para modelar la carga. Este es el modelo menos amortiguador y por lo tanto, conduce a los resultados más pesimistas desde el punto de vista de nivel de distorsión en la red.

Para la aplicación desarrollada, todas las cargas pasivas se descomponen en un conjunto de cargas monofásicas conectadas entre un par de nodos, de forma que al disponer de la admitancia y de la carga actualizada para la frecuencia f, la matriz admitancia de la misma es:

OTROS ELEMENTOS
Otros elementos pasivos, como bancos de condensadores, filtros de armónicos, etc. pueden representarse como arreglos de impedancias entre fase y neutro o entre fase y fase, lo que da la posibilidad de estudiar el efecto de asimetrías en estos elementos.
EJEMPLO
El modelo en coordenadas de fase desarrollado en este trabajo, se ha implementado en una aplicación en Matlab 7,5, capaz de realizar varios estudios básicos entre los que se encuentra el barrido de frecuencia.
Como ejemplo de prueba, se ha tomado un pequeño sistema delta a cuatro hilos de 240 V, que se suministra por un banco de transformadores estrella abierta - delta abierta.
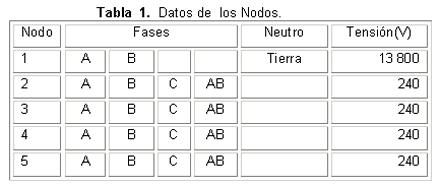
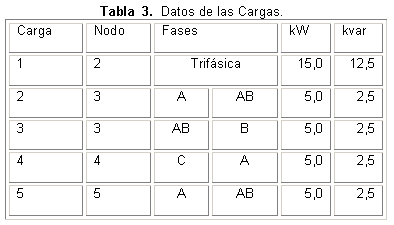
El listado de nodos y las fases disponibles en cada uno se ofrecen en la siguiente tabla 1.
El banco de transformadores de conexión estrella abierta - delta abierta se alimenta del sistema de 13,8 kV que tiene una capacidad de cortocircuito trifásico de 50 MVA y una relación X/R = 10.Tabla 2.
Con excepción de la carga trifásica en el nodo 2, el resto son cargas monofásicas conectadas según la siguiente tabla 3. Todas las cargas se han representado por el modelo serie para el barrido de frecuencia.
En el nodo 2 está conectado un banco de condensadores trifásico de 15 kvar en conexión delta.
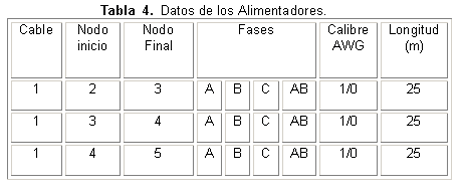
El barrido de frecuencia se realizó desde la frecuencia fundamental de 60 Hz, hasta 1 260 Hz (armónico 21) con incrementos de 1 Hz. Tabla 4.
La figura 4, muestra el comportamiento de las tensiones de línea en el nodo 2, ante una corriente trifásica de 1 pu que se inyecta en las fases A, B, C de dicho nodo.
Es interesante destacar el diferente comportamiento con la frecuencia de las tensiones entre las distintas fases del nodo 2, lo que se debe a las asimetrías estructurales de la red. Figura 5.
Como se ve en la figura 4, hay dos picos de resonancia cercanos a los armónicos 7mo y 15vo, no obstante, las tensiones Ubc y Uca son más incrementadas por la inyección del 7mo armónico, mientras que las tensiones Uab, Ua-ab y Uab-b son más afectadas por el armónico 15.
Con respecto a inyecciones monofásicas entre cada par de terminales del propio nodo 2, pueden destacarse las diferencias entre las figuras 5-7.
Una inyección entre los terminales A-B (figura 5), provoca una resonancia muy pronunciada al armónico 15 para todas las tensiones.
Sin embargo, una inyección entre los terminales C-A (figura 7), provoca una resonancia mayor de las tensiones Ubc y Uca cercana al 7mo armónico y un menor efecto a la tensión Uab para el armónico 15. Por su parte, una inyección entre B-C (figura 6), tiene un efecto semejante al de la inyección trifásica, etc.
CONCLUSIONES
El modelo desarrollado para el barrido de frecuencia es capaz de representar con exactitud las redes desequilibradas que pueden encontrarse en instalaciones industriales, de edificios comerciales y de servicio.
La formulación desarrollada, permite especificar inyecciones armónicas de cualquier tipo: monofásicas o trifásicas de la secuencia deseada. Por lo que puede estudiarse el efecto de las cargas no lineales de acuerdo a sus características y su conexión al circuito.
REFERENCIAS
1.ARRILLAGA, J.; et al., Computer Modeling of Electrical Power Systems, New York, John Wiley & Sons, 1991, ISBN 0-461-10406-X, 423p.
2. ARRILLAGA J.; WATSON, N. R., Computer Modeling of Electrical Power Systems, 2nd Edición, New York, John Wiley & Sons, 2011, ISBN 0-470-87249-0.
3. ARRILLAGA J. ; WATSON, N. R., Power Systems Harmonic, 2nd Edición, New York, John Wiley & Sons, 2003, ISBN 0-470-85129-5, p. 389.
4."Task Force on Harmonics Modeling and Simulation, Modeling and simulation of the propagation of harmonics in electric power networks part I: concepts, models, and simulation techniques". IEEE Transactions on Power Delivery. January 1996, vol.11, n.1, p 452-465, ISSN 0885-8977.
5. IRVING, M. R.; AL-OTHMAN, K., "Admittance matrix models of three-phase transformers with various neutral grounding configurations". IEEE Transactions on Power Systems, August 2003, vol.18, n.3, p.1210-1212, ISSN 0885-8950.
6. MOORTHY, S.; H., David, "A new phase-coordinate transformer model for bus analysis". EEE Transactions on Power Systems, November 2002, vol.17, n.4, p.951-956, ISSN 0885-8950.
7. CHEN, T. H.; Y., W.C., "Modeling and analysis of three-phase four-wire distribution transformers with mid-tap on the secondary side". En: International Conference on Energy Management and Power Delivery, March 998. vol.2, p. 723-727. ISBN 0-7803-4495-2.
8. CHEN, T. H.; et al., "Modeling and analysis of asymmetrical three-phase distribution transformer banks with mid-tap connected to the secondary neutral conductor ". EPRI. 2000, vol.54, p. 83-89.
9. CHEN, T. H.; W.C., "Analysis of Multi-Grounded Four-Wire Distribution Systems Considering the Neutral Grounding". IEEE Transactions on Power Delivery, October 2001, vol.16, n.4, p. 710-717, ISSN 0885-8977.
10. SHORT, T. A., "Electric power distribution handbook, CRC Press". 2004. 762 p. ISBN 0-8493-1791-6.
11. LUÍS SAINZ, M. C.; et al., "Study of Electric System Harmonic Response". IEEE Transactions on Power Delivery, April 2004, vol.19, n.2, p. 868-874, ISSN 0885-8977.
12. LUIS SAINZ, J. P.; et al., "Steinmetz Circuit Influence on the Electric System Harmonic Response". IEEE Transactions on Power Delivery. April 2005, vol.20, n.2, p. 1143-1150. ISSN 0885-8977.
13. LUIS SAINZ, J. P.; et al., "Condensador and Shunt Filter Unbalance Influence on the Electric System Harmonic Response". IEEE Transactions on Power Delivery, April 2005, vol.20, n.2, p. 1522-1531. ISSN 0885-8977.
14. ELECTRICAL TRANSMISSION AND DISTRIBUTION REFERENCE BOOK, W. E. C. 4th Edición, 1964. 832p.
Recibido: Diciembre del 2011
Aprobado: Enero del 2012
Ignacio Pérez Abril. Profesor Titular, Dr. CT. Centro de Estudios Electroenergéticos. Universidad Central "Marta Abreu" de Las Villas. Cuba. e-mail: iperez@uclv.edu.cu