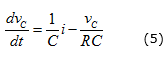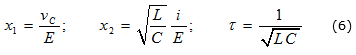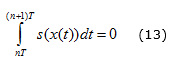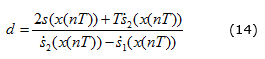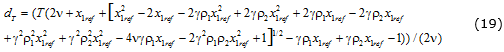APLICACIONES INDUSTRIALES

 

Dinámica de un convertidor boost con inclusión de resistencias parásitas controlado con ZAD

Dynamics of a Boost Converter with Inclusion of Internal Resistance Controlled with ZAD

Dr. Fredy Edimer Hoyos Velasco¹, Dr. Simeón Casanova Trujillo¹, Lic. Darío Del Cristo Vergara Pérez²

¹Universidad Nacional de Colombia
² Institución Educativa San Marcos, San Marcos–Sucre, Colombia

---

RESUMEN

Como dispositivos electrónicos conmutados podemos destacar los convertidores elevador (boost) y reductor (buck), cada uno con su respectiva configuración y aplicaciones en electrónica de potencia. El modelo matemático del convertidor boost se representa por sistemas de ecuaciones diferenciales suaves a tramos pero con discontinuidades en algunos puntos, generando por lo tanto comportamientos muy complejos como cuasi periodicidad y caos cuando este es controlado. El presente artículo propone un nuevo modelo para un convertidor DC-DC tipo boost, en el cual se incluyen resistencias parásitas. Luego el convertidor es controlado usando control no lineal cuasi deslizante ZAD. Simulaciones numéricas en Matlab muestran la presencia de bifurcaciones y comportamiento caótico. A través de los exponentes de Lyapunov se determina el intervalo donde hay presencia de caos. Luego se implementa la técnica de control FPIC para reducir el caos y lograr estabilizar al sistema, esto se evidencia mediante diagramas de bifurcaciones para la tensión y la corriente.

Palabras clave: bifurcación Flip, caos, control no-lineal deslizante ZAD, convertidor boost, PWMC, FPIC.

---

ABSTRACT

As power electronic devices we highlighted the boost and buck converters, each with its respective configuration and power electronics applications. The mathematical model of the boost converter is represented by systems of differential equations piecewise smooth but with discontinuities at some points, thus generating very complex behaviors as quasi-periodicity and chaos when this is controlled. This article proposes a new model for a DC-DC boost converter in which parasitic resistances are included. Then the converter is controlled using non-linear and quasi-sliding ZAD control. Numerical simulations in Matlab show the presence of bifurcations and chaotic behavior. Through Lyapunov exponents it is determines the interval where there is presence of chaos. Then the system is controlled with FPIC to reduce and stabilize chaos, this is evidenced by bifurcation diagrams for voltage and current.

Key Words: Flip bifurcation, chaos, non-linear sliding control ZAD, boost converter, PWMC, FPIC.

---

 

 

INTRODUCCIÓN

El convertidor electrónico boost es un elevador de tensión y si este es controlado en lazo cerrado mediante alguna técnica de control bien diseñada, es robusto y eficiente.

Las principales aplicaciones del convertidor boost se dan en las fuentes de potencia conmutadas y sistemas fotovoltaicos [1]. Sin embargo, la mayor dificultad que presenta este tipo de dispositivos es la estabilidad o inestabilidad del sistema frente a perturbaciones de entrada y salida. Para efectos de implementación de un convertidor, se espera que, teóricamente, el interruptor conmute sólo un número finito de veces por período [2,3]. En el 2001 se reportó por primera vez la técnica de control ZAD (Zero Average Dynamics) la cual es una técnica de control deslizante [4-7], esta consiste en definir una superficie de conmutación y obligar a que el sistema dinámico que gobierna el convertidor evolucione en promedio sobre dicha superficie, además esta técnica garantiza frecuencia fija de conmutación y bajo error de estado estacionario [8,9]. Esta se basa en un diseño donde se fija una salida auxiliar y con base en ella se define una acción de control digital que garantiza promedio cero de error en cada iteración [9-11]. De manera numérica y experimental se ha demostrado que esta técnica funciona bien con el esquema de control de pulso al lado. La superficie de conmutación que usaremos en este artículo se define como una combinación lineal del error en la tensión y el error en la corriente. Este tipo de convertidor fue estudiado sin la inclusión de resistencias parásitas en [12], donde se escogió como superficie de conmutación: ver ecuación (1):

donde: x₁(t) - x_1ref y x₂(t) - x_2ref   representan el error en la tensión y corriente, respectivamente.

De otro lado, con el fin de incluir pérdidas energéticas, en un convertidor tipo buck se han incluido resistencias internas y ha sido controlado con ZAD-FPIC, obteniendo resultados experimentales muy semejantes a los numéricos en [10]. En este artículo se presenta un nuevo modelo matemático más completo para el convertidor tipo boost, donde se incluyen resistencias internas y se espera aportar a futuras investigaciones las cuales estén enfocadas en mejorar la correlación entre resultados numéricos y experimentales para este tipo de convertidor conmutado.

Para identificar el intervalo donde hay presencia de caos se utilizó los exponentes de Lyapunov, estos son una generalización de los multiplicadores característicos, ellos miden el radio de separación de dos órbitas cercanas en el estado espacial.

El control con FPIC puede estabilizar órbitas de periodo uno y superior en sistemas inestables y/o caóticos de una manera simple y sin medición de las variables de estado contrario al control TDAS el cual es muy utilizado para estabilizar este tipo de fenómenos; la técnica FPIC obliga al sistema a que el sistema evolucione al punto fijo. En este sentido se parte del conocimiento previo del punto fijo o el valor de estado estacionario de la señal de control, bien sea de manera analítica o numérica y con base en él se diseña la estrategia de control [10].

En este artículo se presenta un nuevo modelo del convertidor boost, luego este es controlado con una técnica de control no lineal cuasideslizante ZAD, a través de exponentes de Lyapunov se determina el intervalo donde hay presencia de caos y finalmente las zonas de caos e inestabilidad se reducen con la técnica de control FPIC.

El artículo está organizado de la siguiente forma: primero se muestra el modelado matemático del convertidor boost, luego se diseña la técnica de control ZAD aplicada a este convertidor, se muestran resultados numéricos, luego se controla el caos presente en el sistema mediante la técnica de control FPIC y finalmente se presentan unas conclusiones.

MODELO MATEMÁTICO

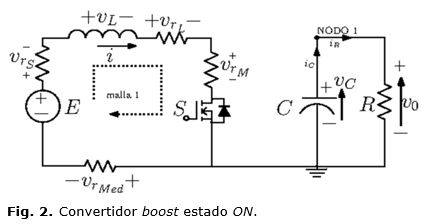
La figura 1, muestra el esquema de un convertidor boost con la inclusión de resistencias parásitas y la caída de tensión en el diodo.

Cuando el interruptor S está cerrado (estado ON) [12], la bobina L almacena energía de la fuente de tensión E, mientras que la carga (R) es alimentada por la energía almacenada en el condensador (C).

En este caso, aplicamos las leyes de Kirchhoff sumando tensiones en la primera malla y haciendo suma de corrientes en el nodo 1 de la figura 2.

Haciendo sumas de tensiones en la malla 1, el modelo queda expresado en las ecuaciones (2) y (3):

Cuando el interruptor está abierto (estado OFF) [12], la corriente sólo puede pasar a través del diodo D y alimenta al condensador C y a la carga.  En este caso, aplicamos las leyes de corrientes de Kirchhoff en la malla 2 como se muestra en la figura 3.

De esta manera, obtenemos las siguientes ecuaciones (4) y (5):

La dinámica del sistema que gobierna al convertidor boost se puede estudiar mejor si adimensionalizamos el sistema. Para lograr esto, se proponen las siguientes relaciones dadas en las ecuaciones (6) y (7).

donde:
R_eq1 = r_s + r_L + r_Med + r_M cuando u = 0

R_eq2 = r_s + r_L + r_Med cuando u = 1

Por lo tanto, el sistema queda expresado matricialmente por la ecuación (8):

Este sistema de ecuaciones puede escribirse de forma compacta como sigue en la ecuación (9):

donde:

La solución de cada topología viene dada por la ecuación (10):

 

siendo: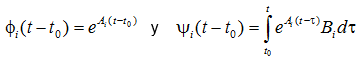

Teniendo en cuenta cada topología y calculando las exponenciales matriciales se tienen las ecuaciones (11) y (12)

donde I₂ es la matriz identidad de tamaño  2 x 2.

Modulación de anchura de pulso

La modulación por ancho de pulso PWM (Pulse-Width Modulation) es una técnica que permite variar el ciclo de trabajo de una señal con el fin de controlar la tensión de la carga, manteniendo fijo el período, o de forma equivalente la frecuencia fija. Para un modulador CPWM, en un período de tiempo  se realizan 2 conmutaciones, de tal manera que un intervalo de tiempo queda dividido en tres subintervalos, donde el primero y el último tienen la misma longitud [2].

ESTRATEGIA DE CONTROL

Técnica de control ZAD

La técnica de control ZAD (Zero Average Dynamics) nos permite calcular el ciclo de trabajo, es decir, el tiempo en el cual el interruptor está abierto o cerrado. Esta técnica consiste en lo siguiente:

1) Definir una superficie de conmutación  en la cual el sistema  evolucionará en promedio. En este trabajo escogemos la superficie dada por la relación (1)
2) Fijar un período T.
3) Imponer que s tenga media cero en cada ciclo, ecuación (13):

Cálculo del ciclo de trabajo

El ciclo de trabajo se calcula mediante la técnica ZAD, aproximando la superficie de conmutación mediante rectas a tramos. Resolviendo la integral dada en ecuación (13), igualando a cero y resolviendo para d  se tiene que el ciclo de trabajo viene dado por la ecuación (14):

En general, d es un número real entre 0 y T. Si se presenta el hecho de que  obligamos al sistema a que evolucione con la configuración u = 1; y si d > T, obligamos al sistema a que evolucione con la configuración u = 0. En cualesquiera de estos dos últimos casos, se dice que el sistema se ha saturado.

Aplicación de Poincaré

La aplicación de Poincaré del convertidor boost controlado con PWMC y técnica ZAD, viene dada por las siguientes relaciones:

1. Si d_n = Є (0,T)  queda definida como la ecuación (15):

2. Si d_n = 0 , el mapa de Poicaré corresponde a la ecuación (16)

3. Si d_n = T , el mapa de Poicaré corresponde a la ecuación (17)

Punto de equilibrio

El punto de equilibrio que se obtuvo para el sistema está dado por el siguiente vector ver  ecuación (18):

donde: 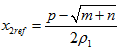siendo , con lo que se obtiene un ciclo de trabajo en estado estacionario (ecuación (19)):

Exponentes de Lyapunov

Los exponentes de Lyapunov son una herramienta matemática por medio de la cual se puede determinar la velocidad de convergencia o divergencia de dos órbitas de una ecuación diferencial, cuyas condiciones iniciales difieren infinitesimalmente una de la otra.

Definición: Sea DF(x) la matriz Jacobiana de la aplicación de Poincaré λ₁(DF(x) el i-ésimo valor propio de DF(x). El exponente de Lyapunov L_i  para cada valor propio viene dado por la ecuación (20):

 

RESULTADOS NUMÉRICOS  

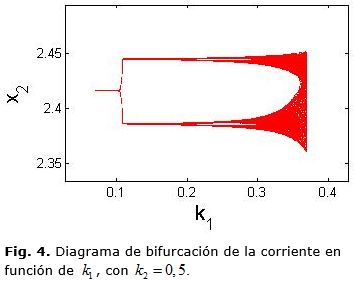
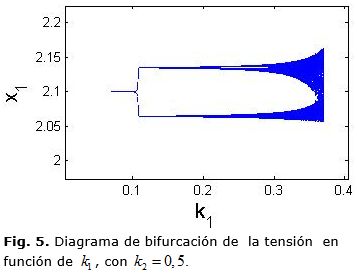
Bifurcación: Cambio cualitativo de un sistema dinámico, ocurrido al variar uno o varios de los parámetros del sistema. Al revisar los valores propios de la matriz jacobiana asociados a la aplicación de Poincaré se obtiene una bifurcación tipo Flip,  dado que uno de estos valores pasa de ser estable a inestable para un valor del parámetro K₁ ≈ 0,0097 . Este tipo de bifurcación pasa por un doblamiento de período. En las figuras 4 y 5, se ha escogido T = 0,18 s, ρ₁ = 0,2782, ρ₂ = 0,2371 y v = 0,0274 y . Como condición inicial se tomó (2.1,2.4159)^T.

Presencia de caos: Para confirmar la presencia de caos en el convertidor boost con resistencias parásitas, numéricamente y a través de la gráfica de exponentes de Lyapunov debemos ver en donde se dan exponentes positivos, ya que la presencia de estos es señal de caos en el convertidor. La figura 6, nos muestra la existencia de caos en el convertidor boost con resistencias parásitas para la variación del parámetro k₁ en el intervalo [0.09796,0.3744]. Las condiciones iniciales escogidas fueron las mismas utilizadas en los diagramas de bifurcación.

Control de caos con FPIC: Para controlar el caos que presenta el convertidor  boost cuando se le introducen resistencias parásitas con ZAD, en esta sección utilizaremos la técnica FPIC (Fixed Point Induced Control).

FPIC: Consideremos un sistema dinámico discreto descrito por un conjunto de ecuaciones (21) y (22)

donde: , suponiendo que el sistema posee un punto fijo (ecuación (22), a l calcular el jacobiano del sistema en este punto fijo se obtiene la ecuación (23):

donde:

Suponiendo que el radio espectral de J_x es menor que uno, entonces existe una señal de control (ecuación (24).

que garantiza la estabilidad del punto fijo (x*,u*) para algún .

Considerando el ciclo de trabajo del sistema como la variable a controlar, se modificó el ciclo de trabajo según la ecuación (25):

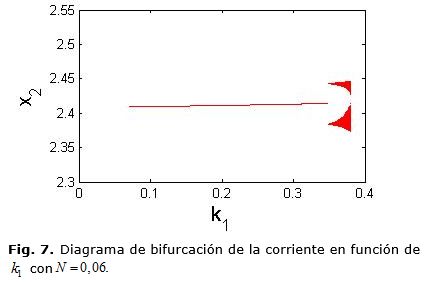
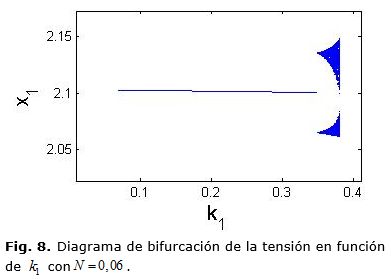
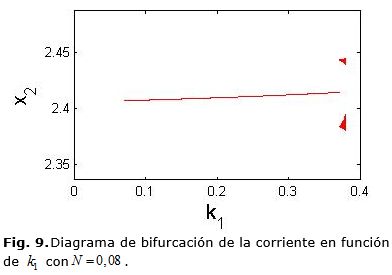
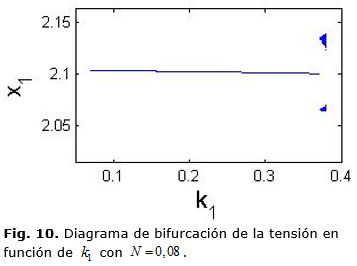
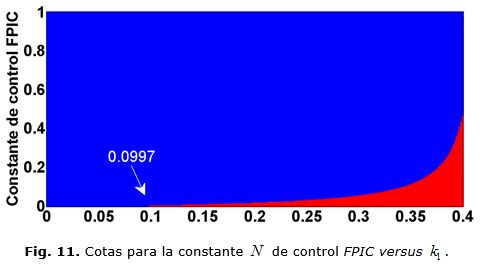
donde: d(k) es el ciclo de trabajo que se va a aplicar, d_T  el ciclo de trabajo obtenido en ecuación (14),  d_E el ciclo de trabajo en estado estacionario y N una constante arbitraria positiva del control FPIC que determina la estabilidad del sistema.  Las figuras 7 y 8,   muestran diagramas de bifurcación, donde se ve que al escoger N = 0,06, disminuye la zona en la que el sistema presenta comportamiento caótico; en las figuras 9 y 10 al escoger N = 0,08 disminuye considerablemente la zona en la que el sistema presenta comportamiento caótico y en la figura 11, se presenta un diagrama de bifurcaciones de codimensión 2 donde se muestran las cotas en las que la técnica FPIC controla el caos, la parte de color azul corresponde a la zona donde el caos se controla y la roja a la presencia de caos.

 

CONCLUSIONES

Se formuló un nuevo modelo matemático para un convertidor boost cuando se le incluyen resistencias parásitas. Se hizo un cambio de variables que permite la reducción de la dimensión del espacio de estados, facilitando el análisis de la dinámica del convertidor boost.

Luego de modelarlo, se procedió a realizar la simulación donde se obtuvieron los diagramas de bifurcaciones mostrados y se pudo contrastar, a través de los valores propios de la matriz Jacobiana, que la bifurcación que aparece es de tipo Flip.

Mediante cálculo numérico de exponentes de Lyapunov se mostró el intervalo para el parámetro  donde hay presencia de caos, luego se procedió a reducir la región de inestabilidad, utilizando la técnica de control FPIC, mostrando su eficiencia en el control de caos.

 

REFERENCIAS

1. Mohan N. Power electronics: A first course. USA:Wiley Global Education; 2011. 38-62 p. ISBN 111821434x, 9781118214343.

2. Mohan N. Advanced electric drives: analysis, control, and modeling using matlab-simulink. USA: John wiley & sons; 2014. 208 p. ISBN 9781118911136.

3. Rashid M. Power Electronics Handbook. third edition. Oxford: Butterworth-Heinemann; 2010. 249-264 p. ISBN 10: 0123820367

4. Shtessel Y, Edwards C, Fridman L, et al. Sliding mode control and observation. New york: Springer; 2014. 43-67 p. ISBN 978-0-8176-4892-3 (print) 978-0-8176-4893-0 (online)

5. Bartolini G, Fridman L, Pisano A, et al. Modern Sliding Mode Control Theory: New Perspectives and Applications. 1 ed. India: Springer-Verlag Berlin Heidelberg; 2008. ISBN 978-3-540-79015-0

6. Angulo F, Burgos J, Olivar G, et al. Two-Parameter Discontinuity-Induced Bifurcation Curves in a Zad-Strategy-Controlled DC-DC Buck Converter. IEEE Transactions on Circuits and Systems - I: Regular Papers. 2008;55(08):2392-2401. ISSN 1549-8328. DOI 10.1109/tcsi.2008.918226.

7. Deivasundari P, Uma G, Ashita S. Chaotic dynamics of a zero average dynamics controlled DC-DC Cuk converter. Power Electronics, IET. 2014;7(2):289-298. ISSN 1755-4535. DOI 10.1049/iet-pel.2012.0737.

8. Taborda J, Burbano D, Angulo F. Quantization Effects on Period Doubling Route to Caos in a Ad-Cntrolled Bck Cnverter. Mathematical Problems in Engineering. 2012;2012:19. DOI 10.1155/2012/526394. Citado 10 de abril de 2015. Disponible en: http://www.hindawi.com/journals/mpe/2012/526394/.

9. El Aroudi A, et al. Stabilizing a Two-Cell Dc-Dc Buck Converter by Fixed Point Induced Control. International Journal of Bifurcation and Chaos. 2009;19(06):2043-2057. DOI 10.1142/s0218127409023895. Citado 1 de abril de 2015. Disponible en: http://www.worldscientific.com/doi/abs/10.1142/s0218127409023895.

10. Angulo F, Burgos JE, Olivar G. Chaos stabilization with TDAS and FPIC in a buck converter controlled by lateral PWM and ZAD. In: Control & Automation. MED '07 Mediterranean Conference on. 2007. p. 1-6. DOI 10.1109/MED.2007.4433846.

11. Angulo F, Fossas E, Seara TM, et al. Bounding the Output Error in a Buck Power Converter Using Perturbation Theory. Mathematical Problems in Engineering. 2008;2008:20. DOI 10.1155/2008/732039. [Citado 10 de abril de 2015 ] Disponible en: http://www.hindawi.com/journals/mpe/2008/732039/.

12. Muñoz J, Osorio G, Angulo F. Boost converter control with ZAD for power factor correction based on FPGA. In: Power Electronics and Power Quality Applications (PEPQA), 2013 Workshop on. p. 1-5. DOI 10.1109/PEPQA.2013.6614942. [Citado 1 de mayo de 2014] Disponible en: http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6614942&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D6614942.

 

 

Recibido: mayo de2015
Aprobado: noviembre de 2015

 

 

AUTORES

Fredy Edimer Hoyos Velasco. Ingeniero Electricista, Doctor en Ingeniería Automática, Profesor Asistente, Universidad Nacional de Colombia. Sede Medellín, Medellín, Colombia. Scientific and Industrial Instrumentation Research Group School of Physics. e-mail: [e-mail]