Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.39 no.3 La Habana sep.-dic. 2018
APLICACIONES INDUSTRIALES
Determinación de los coeficientes globales de transferencia de calor comparando los métodos DTML y ε-NUT
Determination of the overall heat transfer coefficients comparing the LMTD and ε-NTU methods
Andres Adrian Sánchez Escalona1, Ever Góngora Leyva2
1Moa Nickel S.A.–"Pedro Sotto Alba". Moa, Holguín, Cuba.
2Instituto Superior Minero Metalúrgico. Moa, Holguín, Cuba.
RESUMEN
Los procesos de transferencia de energía térmica son problemas importantes a resolver en el campo de la ingeniería. En este ámbito, los intercambiadores de calor son uno de los equipos más usados en la industria. La presente investigación se realizó en un sistema de enfriadores de sulfuro de hidrógeno en explotación, con el objetivo de determinar los coeficientes globales de transferencia de calor mediante dos métodos, aplicando el procedimiento de experimentación pasiva. Con el método de la Diferencia de Temperatura Media Logarítmica (DTML) se obtuvieron valores que oscilaron entre 11,1 y 73,3 W/(m2·K) , comparados con 11,0 y 58,9 W/(m2·K) al aplicar el método de la Efectividad–Número de Unidades de Transferencia (ε-NUT). Aunque los resultados obtenidos fueron similares, para la evaluación térmica del sistema de enfriadores estudiado se recomendó emplear la aproximación de la DTML, utilizada por la mayoría de los investigadores.
Palabras clave: intercambiador de calor; sulfuro de hidrógeno; coeficiente global de transferencia de calor; DTML; ε-NUT.
ABSTRACT
Thermal energy transfer processes are important problems to be solved within the engineering field. In this respect, the heat exchangers are one of the industry most-used equipment. Current research was carried out in an online system of hydrogen sulphide gas coolers, in order to determine the overall heat transfer coefficients by two methods, applying the passive experimentation procedure. Values calculated by means of the Logarithmic Mean Temperature Difference (LMTD) method vary between 11,1 and 73,3 W/(m2·K) , as compared to 11,0 and 58,9 W/(m2·K) when applying the Effectiveness–Number of Transfer Units (ε-NTU) method. Although similar results were obtained, it was recommended to use the LMTD approach for thermal evaluation of studied coolers system, which is used by most researchers.
Key words: heat exchanger; hydrogen sulphide; overall heat transfer coefficient; LMTD; ε-NTU.
INTRODUCCIÓN
Los intercambiadores de calor están presentes en la mayoría de los sistemas térmicos complejos y constituyen el dispositivo más usado para la transferencia de calor sin combustión en los procesos industriales. Se emplean en las plantas de procesamiento químico, de generación de vapor, calefacción y acondicionamiento de aire, preparación de alimentos, refrigeración, entre otras aplicaciones. El monitoreo de sus parámetros óptimos de operación asegura la economía del proceso [1-3].
Existen diversos criterios para evaluar el funcionamiento de los intercambiadores de calor. De ellos, el comportamiento del coeficiente global de transferencia de calor en el transcurso del tiempo se considera un parámetro fiable para determinar con qué rapidez se deterioran las condiciones que favorecen el intercambio térmico [4-5]. Además, su cálculo previo es necesario para determinar el factor de incrustaciones e impacto de las deposiciones en la pérdida de eficiencia de la instalación [6-7].
Para la determinación de los coeficientes globales de transferencia de calor a partir de datos experimentales comúnmente se emplea el método de la Diferencia de Temperatura Media Logarítmica (DTML) [2-8]. El cálculo es sencillo, aunque para intercambiadores de calor multipaso (contracorriente-paralelo) se debe considerar el factor de corrección de la DTML, lo cual conlleva a una expresión extensa que involucra varios parámetros. De las referencias consultadas, sólo Gudmundsson (2011 y 2015) ha utilizado el método de la Efectividad–Número de Unidades de Transferencia (ε-NUT) para determinar experimentalmente los coeficientes globales de transferencia de calor, cuyo cálculo se sustenta en las relaciones NUT publicadas para diferentes configuraciones de intercambiadores de calor [5; 9].
Aunque se conoce que los métodos de la DTML y ε-NUT comparten parámetros comunes y conceptos que arriban a una solución similar con respecto a la capacidad térmica del equipo, pocos investigadores han realizado una comparación detallada de ambos procedimientos. La literatura clásica se limita a plantear que la aproximación de la DTML es útil cuando las temperaturas de entrada y salida de los fluidos son conocidas o se pueden determinar con facilidad, porque de lo contrario el cálculo supone un proceso iterativo de prueba y error. En estos casos, el análisis se efectúa con mayor facilidad utilizando el método de la ε-NUT, basado en el rendimiento o efectividad del intercambiador de calor durante la transferencia de una determinada cantidad de energía térmica [10-12].
Jeter (2006) presentó los fundamentos teóricos de tres métodos convencionales para analizar intercambiadores de calor con flujo cruzado, con objetivos pedagógicos. Según el autor, el enfoque de la Diferencia Media de Temperaturas (DMT) es prácticamente obsoleto. El método de la DTML se prefiere para el dimensionamiento de los intercambiadores de calor, mientras que el de la ε-NUT se selecciona para el análisis del rendimiento y trabajos de simulación [13]. Otro estudio fue realizado por Ramana y SudheerpremKumar (2015) con el propósito de calcular la efectividad en un intercambiador de calor de doble tubo y comparar los resultados de los métodos DTML y ε-NUT con los valores determinados de forma gráfica. Aunque concluyen que los resultados obtenidos son equivalentes, el método de la DTML proporcionó mejor aproximación para la disposición a contracorriente de los fluidos, ocurriendo lo contrario para la disposición en paralelo de las corrientes. La evaluación se realizó para un solo juego de datos, sin modificar ninguna de las variables independientes [14].
A pesar de que la metodología para el análisis de intercambiadores de calor con dos fluidos ha quedado establecida, en la literatura consultada no se hace referencia al estudio de intercambiadores de calor de tubos y coraza enchaquetados, donde interactúan tres fluidos. Cuando los especialistas de las plantas productoras necesitan realizar una evaluación térmica de este tipo de intercambiadores de calor, no tienen definido cual método utilizar para obtener resultados precisos.
Teniendo en cuenta lo anterior, el objetivo de esta investigación es determinar los coeficientes globales de transferencia de calor en un sistema de enfriadores de sulfuro de hidrógeno en explotación, estableciendo una comparación entre los métodos DTML y ε-NUT. Los intercambiadores de calor objeto de estudio tienen uso industrial en las plantas de producción de sulfuro de hidrógeno con alta pureza y en las unidades de recuperación de azufre a partir de la conversión del mencionado reactivo químico (proceso Claus).
MATERIALES Y MÉTODOS
Metodología
La evaluación del proceso de enfriamiento de sulfuro de hidrógeno en intercambiadores de tubos y coraza enchaquetados se efectuó mediante el análisis de los coeficientes globales de transferencia de calor, determinados a partir de datos experimentales. Para el cálculo se emplearon los métodos DTML y ε-NUT.
En intercambiadores con tres fluidos y dos vías principales de intercambio térmico se determinan dos coeficientes globales de transferencia de calor [15-16]. Uno caracteriza el intercambio de calor interno, entre el fluido que circula por los tubos y el que fluye por la coraza; mientras que el otro corresponde al intercambio externo, entre el fluido que circula por la coraza y el que fluye por la chaqueta.
Para simplificación de los cálculos se hicieron los siguientes supuestos [10; 17]:
-
Los intercambiadores de calor operan en condiciones de estado estacionario.
-
Los coeficientes globales de transferencia de calor, así como el calor específico de cada fluido, se mantienen constantes a través del intercambiador de calor.
-
Se desprecia la transferencia de calor hacia el medio ambiente.
-
Los cambios de energía potencial y cinética son despreciables.
-
La transferencia de calor por conducción longitudinal en los fluidos, y en la pared de los tubos y de la coraza, es insignificante.
-
No existen cambios de fase.
-
En un mismo turno de operación el flujo de sulfuro de hidrógeno es constante.
-
Las mediciones del flujo de agua que circula del lado de los tubos y del lado de la chaqueta se efectuaron en ramales comunes, por lo que se asume la mitad del flujo para cada intercambiador, suponiendo que las caídas de presión en los equipos son similares.
Descripción de la instalación y técnica experimental
El sistema estudiado está compuesto por cuatro intercambiadores de calor de tubos y coraza enchaquetados. Cada pareja (dos equipos en serie) fue diseñada para transferir 138 kW de calor, a través de un área de 49,2 m2 . En cada unidad el sulfuro de hidrógeno hace su recorrido del lado de la coraza, en un solo paso, mientras que el agua circula del lado de los tubos, con cuatro pasos, y también por la chaqueta de la coraza. Ver figura 1. Los intercambiadores de calor operan ocho horas en modo de enfriamiento del gas, y luego se sacan de operación para suministrarle vapor (por el lado de los tubos y por la chaqueta) durante cuatro o seis horas con el objetivo de eliminar el azufre incrustado en su interior.
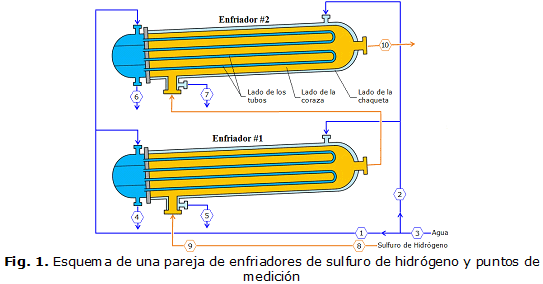
Debido al régimen de producción ininterrumpido en que se encuentra el objeto de estudio se aplicó un experimento pasivo (diseño de investigación no experimental, del tipo longitudinal, de tendencia). Este procedimiento consiste en la observación y registro de las variables de entrada y salida del proceso en el régimen normal de trabajo del objeto investigado, así como en la observación de las variaciones arbitrarias naturales de todas las variables tecnológicas sin la intervención activa del investigador en el transcurso del proceso tecnológico y sin la introducción de perturbaciones preconcebidas. Bajo estas premisas, las mediciones de los parámetros fundamentales que intervienen en el proceso de intercambio térmico se realizaron sin la manipulación de las variables, analizando los mecanismos de transferencia de calor como se manifiestan en su contexto [18].
A continuación se listan los parámetros registrados (puntos de medición según la figura 1):
-
Flujo de agua alimentado del lado de los tubos
-
Flujo de agua alimentado del lado de la chaqueta
-
Temperatura del agua a la entrada del banco de enfriadores
-
Temperatura del agua por los tubos a la salida del enfriador #1
-
Temperatura del agua por la chaqueta a la salida del enfriador #1
-
Temperatura del agua por los tubos a la salida del enfriador #2
-
Temperatura del agua por la chaqueta a la salida del enfriador #2
-
Flujo de sulfuro de hidrógeno alimentado a los enfriadores
-
Temperatura del sulfuro de hidrógeno a la entrada del enfriador #1
-
Temperatura del sulfuro de hidrógeno a la salida del enfriador #2
Los instrumentos correspondientes y sus características técnicas son:
-
Temperaturas: termopozos y termómetros bimetálicos industriales Ashcroft, con precisión de 0,1 K .
-
Flujo de agua: caudalímetro ultrasónico Proline Prosonic Flow 93T, con precisión de 6,3·10-6 m3/s .
-
Flujo de sulfuro de hidrógeno: señal de proceso que se envía a un PLC Siemens S7-400 y mediante Citect SCADA 7.10 la variable se almacena y se muestra en el ordenador del panel de control, con precisión de 10-4 kg/s .
En la experimentación se ejecutaron tres observaciones en días alternos, durante ocho horas a partir de la puesta en funcionamiento de una misma pareja de intercambiadores de calor en modo de enfriamiento. Durante cada ciclo se ejecutaron 20 mediciones de las variables tecnológicas en cada intercambiador de calor, obteniéndose un juego de datos con 120 registros. Para disminuir los errores aleatorios y accidentales de observación (de paralaje, del fenómeno físico y de reflejo) se efectuaron tres réplicas.
La temperatura del gas a la salida del enfriador #1 se determinó mediante un balance de energía, según muestra la ecuación (1) [15]. De forma análoga, la temperatura del gas a la salida del enfriador #2 se comprobó utilizando la misma ecuación.
Donde: T [K] es la temperatura; ![]() [kg/s] es el flujo másico; y Cp [J/(kg·K)] el calor específico a presión constante. Los subíndices a, b y c identifican los fluidos del lado de los tubos, de la coraza y de la chaqueta, respectivamente; mientras que 1 y 2 se refieren a las condiciones de entrada y de salida de cada corriente.
[kg/s] es el flujo másico; y Cp [J/(kg·K)] el calor específico a presión constante. Los subíndices a, b y c identifican los fluidos del lado de los tubos, de la coraza y de la chaqueta, respectivamente; mientras que 1 y 2 se refieren a las condiciones de entrada y de salida de cada corriente.
Determinación de los coeficientes globales mediante el método de la DTML
La determinación de los coeficientes globales de transferencia de calor, empleando el método de la DTML, se realiza mediante la ecuación (2). El área de transferencia de calor se conoce por catálogo, mientras que la cantidad de calor transferida durante el proceso, la diferencia de temperatura media logarítmica y su factor de corrección se calculan a partir de los datos experimentales: flujos másicos de cada corriente, así como las temperaturas de entrada y salida de los fluidos [3; 7; 14].
Donde: U [W/(m2·K)] es el coeficiente global de transferencia de calor; Q [W] representa el calor transferido; A [m2] es el área de transferencia; ΔTml [K] es la diferencia de temperatura media logarítmica; y F su factor de corrección.
Para el intercambio de calor interno (tubos-coraza) la diferencia de temperatura media logarítmica (ΔTml i) se determina a través de la ecuación (3), basada en un equipo multipaso. El calor que se transfiere (Qi) es absorbido por el agua que circula del lado de los tubos, y en su cálculo se emplea la ecuación (4), debido a que no ocurren cambios de fase [10].
En cambio, para el intercambio de calor externo (coraza-chaqueta) la diferencia de temperatura media logarítmica (ΔTml e) se calcula mediante la ecuación (5), establecida para un intercambiador de calor con flujos a contracorriente. En este caso el calor que se transfiere (Qe) es absorbido por el agua del lado de la chaqueta, y se determina según la ecuación (6) [10].
El factor de corrección de la diferencia de temperatura media logarítmica es igual a la unidad (F=1) para flujos en contracorriente o paralelo. Sin embargo, en intercambiadores de calor de tubos y coraza multipaso se determina mediante las ecuaciones (7) y (8), para cualquier número de pasos por la coraza y número par de pasos por los tubos, cuando R ≠1 [11; 19].
Donde: el parámetro S es utilizado para simplificar la ecuación de cálculo del factor de corrección; R es la relación entre las diferencias de temperatura, calculada mediante la ecuación (9); P es la efectividad de las temperaturas, según la ecuación (10); y N es el número de pasos por la coraza.
Determinación de los coeficientes globales mediante el método ε-NUT
La determinación de los coeficientes globales de transferencia de calor, empleando el método ε-NUT, se realiza mediante la ecuación (11). El área de transferencia de calor es conocida, mientras que la capacitancia térmica mínima y la relación de las capacitancias térmicas se calculan a partir de los datos experimentales. El número de unidades de transferencia se determina en función del tipo de intercambiador, la efectividad térmica y la relación de las capacitancias térmicas [9].
Donde: Cmín [J/(s·K)] es la capacitancia térmica mínima; y NUT es el número de unidades de transferencia. La capacitancia térmica de cada corriente se determina a través de la ecuación (12).
En el caso de la transferencia de calor interna (tubos-coraza) el número de unidades de transferencia (NUTi) se calcula basado en un intercambiador multipaso, según la ecuación (13) [10].
Sin embargo, para la transferencia de calor externa (coraza-chaqueta), al determinar el número de unidades de transferencia (NUTe) se considera un intercambiador a contracorriente y se utiliza la ecuación (14) [10].
Donde: ε [%] es la eficiencia térmica; y Cr la relación de las capacitancias térmicas. El subíndice i se refiere al intercambio de calor interno; mientras que e representa al externo.
La eficiencia térmica se define como la proporción entre la magnitud real de transferencia de calor y la máxima transferencia de calor posible [10-12]. Por lo tanto, para el intercambio de calor interno se determina mediante la ecuación (15), y para el externo según la ecuación (16).
La relación de las capacitancias térmicas se calcula por medio de la ecuación (17) [10-11].
Donde: Cmáx [J/(s·K)] es la capacitancia térmica máxima.
Cuando el método ε-NUT se utiliza para determinar los coeficientes globales de transferencia de calor basados en datos experimentales se deben conocer o poder estimar las temperaturas de entrada y de salida de ambos fluidos, a diferencia de cuando el método se emplea para calcular el calor transferido y las temperaturas de salida en el intercambiador (problema del Rating).
RESULTADOS Y DISCUSIÓN
Aplicación del método de la DTML
En la figura 2, se muestra el comportamiento de los coeficientes globales de transferencia de calor determinados mediante el método de la DTML. Los cálculos se realizaron para tres valores de flujo de sulfuro de hidrógeno.
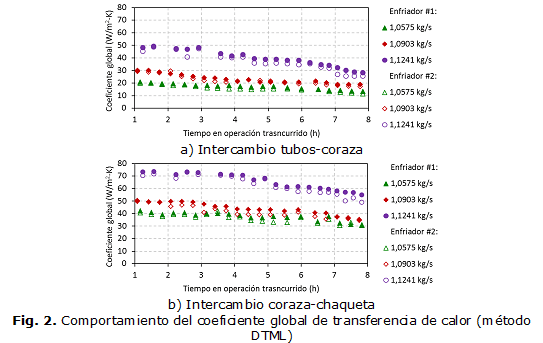
En las ocho horas que dura el ciclo de enfriamiento se observó tendencia decreciente del coeficiente global de transferencia de calor, debido fundamentalmente a un incremento de las incrustaciones de azufre dentro de los intercambiadores de calor. Con el transcurso del tiempo la acumulación de las partículas de azufre que se van separando del gas crece sobre las paredes de los tubos y de la coraza, formando capas “de aislamiento” sobre las superficies de transferencia de calor que actúan en detrimento del intercambio térmico, y provocan una disminución del coeficiente global entre 7,5 y 20,8 W/(m2·K) . Otras causas que provocan cambios del coeficiente global son las variaciones de flujo y de las propiedades termo-físicas de los fluidos, pero su incidencia es menor comparada con la influencia de las incrustaciones. Se determinó que los cambios de presión y temperatura de los fluidos, al incidir en sus propiedades termo-físicas, provocan variaciones máximas del coeficiente global de transferencia de calor equivalentes a 1,1 W/(m2·K) para el intercambio térmico tubos-coraza y 3,6 W/(m2·K) para el intercambio coraza-chaqueta.
Los valores del coeficiente global de transferencia de calor mejoran con el incremento del flujo másico de sulfuro de hidrógeno, ya que al aumentar la velocidad del gas del lado de la coraza se incrementa el coeficiente individual de transferencia por convección y decrece la resistencia térmica de las incrustaciones. Aunque la mayor transferencia de calor tiene lugar en el enfriador #1, el comportamiento del coeficiente global es similar en el enfriador #2.
Aplicación del método ε-NUT
En la figura 3, se muestra el comportamiento de los coeficientes globales de transferencia de calor determinados mediante el método ε-NUT. Al aplicar este procedimiento (para los mismos datos experimentales) se obtuvieron valores comparables con los obtenidos mediante el método de la DTML. La disminución de los coeficientes globales de transferencia de calor al finalizar los ciclos de trabajo osciló entre 6,9 y 16,7 W/(m2·K) .
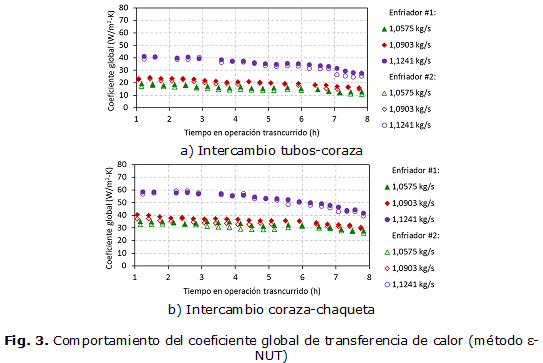
Para incrementar los coeficientes globales de transferencia de calor y, por consiguiente, mejorar el proceso de intercambio térmico en los enfriadores de sulfuro de hidrógeno, se recomienda: acortar el tiempo planificado para el ciclo de enfriamiento; desmontar el haz de tubos de cada intercambiador de calor, ejecutar limpieza y montar nuevamente; o sustituir los haces de tubos en explotación por nuevas unidades. Estas acciones contribuirán a minimizar el impacto de las incrustaciones en la pérdida de eficiencia térmica de la instalación. También se sugiere incrementar el flujo de agua alimentado a cada enfriador por encima de 1,167 kg/s , del lado de los tubos, para alcanzar el régimen turbulento (Re>4000).
Comparación de los métodos empleados
Ambos métodos revelan tendencia decreciente del coeficiente global de transferencia de calor con el transcurso del tiempo, así como mayores valores de este parámetro con el incremento del flujo másico de sulfuro de hidrógeno. Sin embargo, los valores de los coeficientes globales calculados mediante el método de la DTML son superiores a los determinados mediante el método de la ε-NUT. En la tabla 1, se muestran las variaciones calculadas durante la comparación cuantitativa de ambos procedimientos.
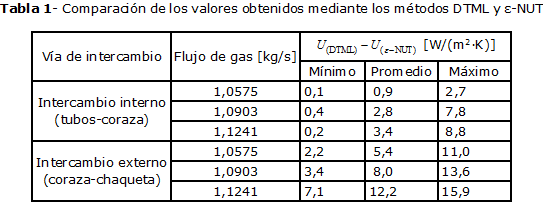
La mayoría de los autores que han evaluado la influencia de las incrustaciones en la pérdida de eficiencia de intercambiadores de calor, a partir de la determinación de los coeficientes globales, emplearon el método de la DTML [1-2; 6-8; 12]. Utilizar los coeficientes globales de transferencia de calor calculados mediante el método de la ε-NUT, inferiores a los determinados mediante la DTML, trae consigo la estimación de valores conservadores de resistencia térmica de las incrustaciones, que conllevan al sobredimensionamiento de la instalación.
En el caso de la vía externa de intercambio de calor, la determinación de los coeficientes globales prescinde del factor de corrección de la DTML, por considerarse como un intercambiador con flujos a contracorriente (F=1). Esto hace más directo y preciso el cálculo basado en el método de la DTML, según las ecuaciones (2) y (5), si se compara con las ecuaciones (11) y (14) fundamentadas en el método ε-NUT. La propagación de los errores de medición se acentúa con la última solución.
El método ε-NUT se emplea principalmente en intercambiadores de calor con flujo cruzado, ya que para esta configuración no se constató una expresión analítica que permita programar y determinar con precisión el factor de corrección de la DTML. Un requisito esencial para obtener resultados confiables mediante el método ε-NUT es seleccionar apropiadamente la función que mejor caracterice al intercambiador de calor analizado.
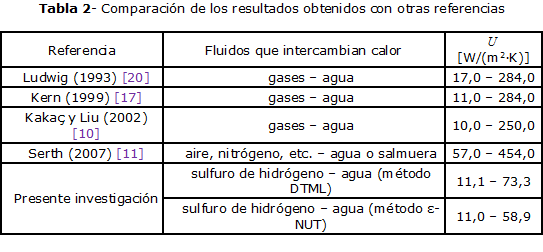
Varios autores han establecido rangos de valores preliminares del coeficiente global en intercambiadores tubulares para la transferencia de calor entre gases y agua, pero ningún estudio consultado hace referencia al intercambio térmico entre sulfuro de hidrógeno y agua. En la tabla 2, se comparan los resultados obtenidos con los publicados por otros investigadores. Estos valores se emplean durante la evaluación de intercambiadores de calor para realizar un estimado rápido del área de transferencia requerida, despejando en la ecuación (2), por lo que asumir un valor más preciso del coeficiente global de transferencia de calor mejorará la exactitud de los cálculos.
CONCLUSIONES
Tanto el método de la DTML como el de la ε-NUT se pueden emplear para la determinación de los coeficientes globales de transferencia de calor partiendo de datos experimentales. Sin embargo, el método de la DTML es el utilizado por la mayoría de los investigadores y se recomienda para realizar la evaluación térmica del sistema de enfriadores objeto de estudio.
Mediante el método de la DTML se obtuvieron valores de los coeficientes globales de transferencia de calor que oscilaron entre 11,1 y 73,3 W/(m2·K) , mientras que al aplicar el método ε-NUT los resultados fluctuaron entre 11,0 y 58,9 W/(m2·K) . Los coeficientes determinados para el intercambio térmico entre sulfuro de hidrógeno y agua permiten delimitar el rango de valores preliminares publicado por otros autores para gases y agua, en intercambiadores tubulares.
REFERENCIAS
[1].Gerami, A. y Darvishi, P. “Modeling of the deposit formation on shell and tube heat exchanger of Hasheminejad Gas Refinery Plant”. Indian Journal of Science & Reserarch. 2014, vol. 5, n. 1, p. 382-388. [Consultado el: 6 de noviembre de 2017]. Disponible en: https://www.ijsr.in/upload/ 1451074177Microsoft%20Word%20-%20paper-TALEII%20NEW-one.pdf. ISSN: 2250-0138.
[2].Lebele-Alawa, B. T. y Ohia, I. O. “Influence of fouling on heat exchanger effectiveness in a polyethylene plant”. Energy and Power. 2014, vol. 4,n. 2, p. 29-34. [Consultado el: 6 de noviembre de 2017]. Disponible en: http://article.sapub.org/10.5923.j.ep.20140402.01.html. DOI: 10.5923/j.ep.20140402.01.
[3].Igwe, J. E. y Agu, C. S. “Comparative analysis of different fluids in shell pass and two tube heat exchanger”. American Journal of Engineering Research (AJER). 2016, vol. 5, n. 8, p. 81-87. Consultado el: 6 de noviembre de 2017. Disponible en: http://www.ajer.org/papers/v5(08)/ M0508081087.pdf. ISSN: 2320-0847.
[4].Friebel, T.; Haber, R. y Schmitz, U. “Lifetime estimation of heat exchangers with consideration of on-line cleaning”. En: 18th International Conference on Process Control. Tatranská Lomnica, Eslovaquia. 2011, p. 434-439. [Consultado el: 8 de noviembre de 2017]. Disponible en: https://www.kirp.chtf.stuba.sk/pc11/ data/papers/062.pdf. ISBN: 978-80-227-3517-9.
[5].Gudmundsson, O. “Detection of fouling in heat exchangers using model comparison”. Tutores: Palsson, O. P. y Palsson, H. Tesis Doctoral. Facultad de Ingeniería Industrial, Ingeniería Mecánica y Ciencias de la Computación, Universisdad de Islandia, Reykjavik. 2015. Consultado el: 13 de noviembre de 2017. Disponible en: https://skemman.is/bitstream/1946/23909/1/Oddgeir%20-%20PhD%20thesis%20wp.pdf. ISBN: 978-9935-9243-8-4.
[6].Torres-Tamayo, E.; Retirado-Mediaceja, Y. y Góngora-Leyva, E. “Coeficientes de transferencia de calor experimental para el enfriamiento de licor en intercambiadores de placas”. Ingeniería Mecánica. 2014, Vol. 17, No. 1, p. 68-77. Consultado el: 13 de noviembre de 2017. Disponible en: http://www.ingenieriamecanica.cujae.edu.cu/index.php/revistaim/ article/view/479/835. ISSN: 1815-5944.
[7].Torres-Tamayo, E.; Díaz, E. J.; Cedeño, M. P.; Vargas, C. L.; Peralta, S. G. y Falconi, M. A. “Overall heat transfer coefficients, pressure drop and power demand in plate heat exchangers during the amonia liquor cooling process”. International Journal of Mechanics. 2016, Vol. 10, p. 342-348. Consultado el: 13 de noviembre de 2017. Disponible en: http://www.naun.org/main/NAUN/mechanics/2016/b022003-204.pdf. ISSN: 1998-4448.
[8].Jaglarz, G. y Taler, D.. “Experimental study of fouling in plate heat exchangers in district heating systems”. Journal of Power Technologies. 2015, Vol. 95, p. 42-46. Consultado el: 13 de noviembre de 2017. Disponible en: http://papers.itc.pw.edu.pl/index.php/ JPT/article/viewFile/656/648.
[9].Gudmunsson, O.; Palsson, O. P.; Palsson, H. y Jonsson, G. R. “Comparison of fouling detection between a physical method and a black box model”. En: International Conference on Heat Exchanger Fouling and Cleaning. Isla de Creta, Grecia. 2011, p. 391-398. Consultado el: 13 de noviembre de 2017. Disponible en: http://heatexchanger-fouling.com/papers/ papers2011/57_Gudmundsson_F.pdf.
[10].Kakaç, S. y Lui, H.`` Heat exchangers. Selection, rating and thermal design´´.2da ed. Nueva York: CRC Press, 2002. 491 p.33-68, 302. ISBN: 0-8493-0902-6.Disponible en: https://books.google.com.cu/books?hl=es&lr=&id=sJXpvP6xLZsC&oi=fnd&pg=PP1&dq=Heat+exchangers.+Selection,+rating+and+thermal+design&ots=MKh-YLnG6D&sig=RINXBr9By8j_6JXAWAIzQzRGZfI&redir_esc=y#v=onepage&q=Heat%20exchangers.%20Selection%2C%20rating%20and%20thermal%20design&f=false
[11].Serth, W. R. ``Process Heat Transfer Principles and Applications´´. Oxford, Reino Unido: Elseiver Ltd., 2007. 755 p.86-120. ISBN: 978-0-12-373588-1.Disponible en: https://books.google.com.cu/books?hl=es&lr=&id=phlk1tMcl9sC&oi=fnd&pg=PP1&dq=%60Process+Heat+Transfer+Principles+and+Applications&ots=96ImHLqg0I&sig=DbmyIN4TXnEzcrCghE_jJCW5lig&redir_esc=y#v=onepage&q=%60Process%20Heat%20Transfer%20Principles%20and%20Applications&f=false
[12].Ardsomang, T.; Hines, J. W. y Upadhyaya, B. R. “Heat exchanger fouling and estimation of remaining useful life”. En: Annual Conference of Prognostics and Health Management Society. Knoxville, Estados Unidos. 2013, p. 1-9. [Consultado: 7 de diciembre de 2017]. Disponible en: http://ftp.phmsociety.org/sites/ phmsociety.org/files/phm_submission/2013/phmc_13_031.pdf.
[13].Jeter, S. M. “Effectiveness and LMTD correction factor of the cross flow exchanger: a simplified and unified treatment”. En: ASEE Southeast Section Conference. Atlanta, Estados Unidos. 2013, p. 1-10. [Consultado el: 7 de diciembre de 2017]. Disponible en: http://se.asee.org/proceedings/ASEE2006/ P2006092JET.pdf.
[14].Ramana, P. V. y SudheerpremKumar, B. “Development of a practical model to find out effectiveness of heat exchanger and its comparison with standard values”. International Journal of Innovative Research and Creative Technology (IJIRCT). 2015, vol. 1, n. 5, p. 468-472. [Consultado el: 8 de diciembre de 2017]. Disponible en: http://www.ijirct.org/papers/IJIRCT1201101.pdf. ISSN: 2454-5988.
[15].Ghiwala, T. M. y Matawala, V. K. “Sizing of triple concentric pipe heat exchanger”. International Journal of Engineering Development and Research. 2014, vol. 2, n. 2, p. 1683-1692. [Consultado el: 7 de diciembre de 2017]. Disponible en: https://www.ijedr.org/ papers/IJEDR1402067.pdf. ISSN: 2321-9939.
[16].Saurabh, D.; Tamkhade, P. K. y Lele, M. M. “Design Development and Heat Transfer Analysis of a Triple Concentric Tube Heat Exchanger”. International Journal of Current Engineering and Technology. 2016, vol. 5, n. especial, p. 246-251. [Conultado el: 8 de diciembre de 2017]. Dsiponible en: http://inpressco.com/wp-content/uploads/2016/07/Paper47246-251.pdf. ISSN: 2277-4106.
[17].Kern, D. Q. Procesos de Transferencia de Calor. 31ra reimpresión. México D.F.: Compañía Editorial Continental S.A. de C.V., 1999. 980 p. 112-127, 945. ISBN: 968-26-1040-0.Disponible en: http://www.libun.edu.pe/carrito/principal.php/articulo/00094837
[18].Hernández-Sampieri, R.; Fernández-Collado, C. y Baptista-Lucio, M. P. Metodología de la Investigación. 5ta ed. México D.F.: McGraw-Hill, 2010. 613 p.149-162. ISBN: 978-607-15-0291-9.Disponible en: https://www.google.com/search?q=978-607-15-0291-9&ie=utf-8&oe=utf-8
[19].Obregon-Quinones, L. G.; Arrieta-Viana, L. F. y Valencia-Ochoa, G. E. “Thermal Design and Rating of a Shell and Tube Heat Exchanger Using a Matlab® GUI”. Indian Journal of Science and Technology. 2017, vol. 10, n. 25, p. 1-9. [Conultado el: 14 de noviemnre de 2017]. Disponible en: www.indjst.org/ index.php/indjst/article/download/.../80790. ISSN: 0974-5645. DOI: 10.17485/ijst/2017/v10i25/114038.
[20].Ludwig, E. E. Applied Process Design for Chemical and Petrochemical Plants. vol 3.
2da ed. Houston, Texas: Gulf Publishing Company, 1993. 500 p.71. ISBN: 0-87201-788-5.Disponible en: https://books.google.com.cu/books?hl=es&lr=&id=LWkyRHJiDJUC&oi=fnd&pg=PP2&dq=Applied+Process+Design+for+Chemical+and+Petrochemical+Plants&ots=upcTORyJ_M&sig=AgzFqOBjsmYauLHfrgeDVgE5Aew&redir_esc=y#v=onepage&q=Applied%20Process%20Design%20for%20Chemical%20and%20Petrochemical%20Plants&f=false
Recibido: 1/2/2018
Aprobado: 2/5/2018
Andres Adrian Sánchez Escalona, Moa Nickel S.A.–“Pedro Sotto Alba”. Moa, Holguín, Cuba. E-mail: aescalon@moanickel.com.cu













 (5)
(5) (7)
(7)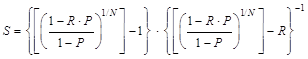 (8)
(8) (13)
(13)
