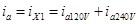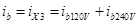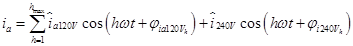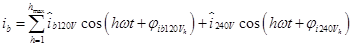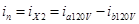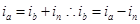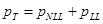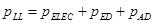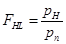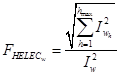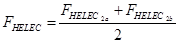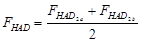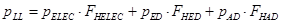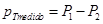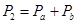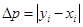Artículo de investigación

Validación experimental para la estimación de las pérdidas en transformadores monofásicos y carga no lineal

Experimental validation for the estimation of losses in single-phase transformers and non-linear load

0000-0002-0174-5309Frank Grau Merconchini^{I  *}  , 0000-0002-2672-239XOrestes Hernández Areu^II  , 0009-0008-2179-6809Eduardo López Pérez^I  , 0000-0001-8515-8998Nelson Alexey Castro Torres^I 

^I Universidad de Oriente (UO). Santiago de Cuba, Cuba

^II Universidad Tecnológica de la Habana, José Antonio Echeverría (CUJAE). La Habana, Cuba

RESUMEN

Cuando se emplean transformadores monofásicos con derivación central en las redes de distribución, para dar servicio a cargas no lineales, estos suelen estar cargados de forma desigual entre los extremos del devanado secundario, haciendo que circule una corriente por el neutro con un contenido armónico elevado y, que las corrientes que circulan por ambas mitades del devanado secundario, sean distintas en amplitud y forma de onda. Para determinar con mayor precisión la influencia de la distorsión armónica en las pérdidas, se propone un modelo a partir del empleo de factores de pérdidas de distorsión promedio. Este modelo, fue validado mediante un esquema que combina cargas lineales y no lineales, para distintos valores de cargabilidad del transformador, obteniéndose que la diferencia entre las pérdidas calculadas y las medidas en el laboratorio no exceden el 5 % en ninguna de las pruebas realizadas, arrojando un error absoluto medio de 2,04 W.

Palabras-clave: pérdidas; distorsión armónica; transformador monofásico; validación experimental

ABSTRACT

When single-phase center tapped transformers are used in distribution networks to serve non-linear loads, they are usually loaded unequally between the ends of the secondary winding, causing a current to flow through the neutral with a high harmonic content and, that the currents that circulate through both halves of the secondary winding are different in amplitude and waveform. To determine more precisely the influence of harmonic distortion on losses, a model is proposed using average distortion loss factors. This model was validated using a scheme that combines linear and non-linear loads, for different loadability values of the transformer, obtaining that the difference between the calculated losses and those measured in the laboratory does not exceed 5% in any of the tests carried out. yielding a mean absolute error of 2,04 W.

Key words: losses; harmonic distortion; single-phase transformer; experimental validation

Introducción

La calidad de la energía eléctrica, puede definirse como la ausencia de disturbios que provoquen una deformación de la onda sinusoidal pura de tensión y de corriente ^[1, ², ^3]. La existencia de estos disturbios puede generar un incremento en las pérdidas, la reducción de la vida útil del equipamiento, disparos en las protecciones, el incremento en el costo de las instalaciones por la necesidad de sobredimensionar sus elementos, e incluso puede llegar a comprometer la continuidad del servicio eléctrico. La baja calidad de la energía eléctrica, se ve reflejada en el incremento de indicadores tales como la desviación de la tensión, la desviación de la frecuencia, la asimetría y el desbalance de las tensiones y de las corrientes, así como en las deformaciones de las señales de tensión y de corriente producidas por la presencia de armónicos.

A pesar de que las cargas no lineales pueden distorsionar la forma de onda de las tensiones, su principal efecto está en la distorsión que producen sobre las señales de corriente que le demandan a la fuente de alimentación. La presencia de armónicos en las corrientes, provoca un incremento en las pérdidas de los alimentadores y los transformadores en las redes de distribución, disminuyendo su eficiencia y acortando la vida útil de los mismos ^[4, ⁵, ^6].Investigaciones desarrolladas han constatado que, las pérdidas asociadas a las componentes armónicas de las corrientes en circuitos de distribución pertenecientes a servicios exclusivos de la industria, llegan a representar entre un 20 y un 22 % de las pérdidas de transformación y que la mayor parte de los problemas técnicos que se presentan en estos circuitos, son debido a la polución armónica en los mismos y a la no existencia de medidas de control para su mitigación ^[2, ⁷, ^8].

El incremento de la presencia de las cargas no lineales y sus efectos en los elementos de los sistemas, dio lugar a que, en el año 1998, fuera aprobada en el comité de transformadores del Institute of Electrical and Electronics Engineers (IEEE) la norma ANSI/IEEE C57.110 ^[9], que provee un procedimiento para determinar la reducción de la capacidad y la corriente permisible del transformador cuando trabaja con corrientes no sinusoidales. La norma describe dos métodos. El primero está orientado a la etapa de diseño de los transformadores, para lo cual se requiere de acceso a información detallada sobre la distribución de la densidad de pérdidas dentro de los devanados. El segundo método está destinado a los usuarios (para ser empleado en la etapa de explotación), para lo cual se requiere tener acceso a los datos de las pruebas de las máquinas y, por consiguiente, puede arrojar datos menos precisos que el primer método.

Las cargas residenciales y de servicios son no lineales por naturaleza. La gran cantidad de equipos electrodomésticos (fundamentalmente los equipos electrónicos), las lámparas y luminarias con componentes electrónicos son la causa fundamental de este comportamiento. Los transformadores por su parte, se ven afectados por la circulación de corrientes con un contenido armónico elevado, las cuales provocan un incremento en las pérdidas eléctricas y adicionales y, por tanto, en la temperatura de trabajo, lo que trae consigo el deterioro del aislamiento y la reducción de la vida útil de la máquina ^[10]. En las redes de distribución secundarias (RDS), los transformadores de distribución monofásicos brindan servicio de 120 V y 240 V. Comúnmente, las cargas de 120 V son cargas puntuales, de fuerza y alumbrado, por lo que la potencia varía en el tiempo y presentan niveles de desequilibrio considerables (ver figura 1).

Fuente: Elaboración propia

Fig. 1 Transformador monofásico con derivación central y cargas con distintos niveles de tensión.  

Las corrientes en las ramas secundarias pueden ser descritas como la suma de las componentes de las corrientes que demandan las cargas de 120 V (conectadas en ambas mitades del devanado secundario X1 - X2 y X2 - X3) y 240 V (entre los extremos del devanado secundario X1 - X3), de la forma en que aparece expresado en las ecuaciones (1, 2).

(1)

(2)

El valor de las componentes de la corriente para la carga de 240 V es el mismo en ambos extremos del secundario del transformador (i _a240V = i _b240V = i _240V ). En cambio, las componentes de las corrientes para las cargas de 120 V suelen ser distintas en amplitud y niveles de distorsión. Entonces, las corrientes de fases pueden ser expandidas en su serie de Fourier de acuerdo a las (ecuaciones 3, 4).

(3)

(4)

Donde:

h	es el orden del armónico en análisis
ω	es la frecuencia angular
φ	es el ángulo de desplazamiento de fase para la corriente

La corriente por el neutro (i_n), será la resultante de la diferencia entre de las componentes de las corrientes de carga de 120 V, tal y como se presenta en la ecuación (5):

(5)

Cuando las cargas de 120 V están equilibradas, las corrientes i _a120V e i _b120V tienen igual amplitud, pero al encontrarse defasadas 180° entre sí su resultante i _n es igual a cero.Las corrientes que circulan por ambas mitades del devanado secundario resultan en la combinación de las corrientes en ambas fases del secundario del transformador, correspondiéndose con la sumatoria de los armónicos individuales que oscilan a la misma frecuencia, cumpliendo así con la ecuación (6):

(6)

De esta forma, la corriente en cada mitad del devanado secundario se ve afectada por la distorsión armónica que introduce la carga no lineal conectada a la otra mitad del devanado secundario del transformador. Entonces, la norma ANSI/IEEE C57.110 para la estimación de pérdidas en transformadores monofásicos de dos devanados en presencia de distorsión armónica no puede ser directamente empleada, aun cuando las corrientes y sus respectivos espectros de distorsión pueden ser medidos con un instrumento registrador (analizador de red) en cada fase de la carga, por lo que se requieren realizar determinadas consideraciones.

Materiales y métodos

Modelo analítico para la estimación de las pérdidas basado en factores de pérdidas armónicas

El efecto de los armónicos en transformadores está presente tanto en las pérdidas de cobre como en las pérdidas adicionales. En general, las pérdidas en los transformadores pueden ser separadasen pérdidas con carga y pérdidas en vacío ^[9, ^11]. Vea ecuación (7).

(7)

Donde:

pNLL	son las pérdidas en vacío (non load loss)
pLL	son las pérdidas con carga (load loss)

Mientras las pérdidas de vacío permanecen constantes en tanto no se experimenten valores de distorsión armónica total en las tensiones (THDv) superiores al 8% ^[9, ^12], las pérdidas con carga sí se elevan como resultado de la distorsión armónica de las corrientes. El valor de las pérdidas de vacío de cada transformador puede ser determinada mediante el ensayo de vacío en el laboratorio. Las pérdidas con carga pueden dividirse en pérdidas eléctricas (pELEC) y pérdidas adicionales totales (pADT). Pérdidas adicionales, por corrientes de Eddy o corrientes parásitas, debido al flujo electromagnético extraviado en el devanado, núcleo, abrazadera del núcleo, campo magnético, pared del tanque y otras partes estructurales del transformador.

Las pérdidas adicionales del devanado incluyen pérdidas aisladas de corrientes de Eddy en los conductores del devanado y las pérdidas debido a la circulación de corrientes entre devanados paralelos o aislados. Estas pérdidas aumentarán en proporción al cuadrado de la corriente de carga y al cuadrado de la frecuencia. En la ecuación (8), se muestra la expresión de las pérdidas con carga del transformador.

(8)

Donde:

pELECT	son las pérdidas eléctricas en los devanados
pED	son las pérdidas por corrientes parásitas en los devanados
pAD	son las pérdidas adicionales en las partes del transformador

Las pérdidas adicionales totales están compuestas por las pérdidas de Eddy o por corrientes parásitas, debido al flujo electromagnético extraviado en el devanado, núcleo, abrazadera del núcleo, campo magnético, pared del tanque y otras partes estructurales del transformador. Las pérdidas adicionales del devanado incluyen pérdidas aisladas de corrientes de Eddy en los conductores del devanado y otras pérdidas adicionales debido a la circulación de corrientes entre devanados paralelos o aislados. Esta pérdida aumentará en proporción al cuadrado de la corriente de carga y al cuadrado de la frecuencia, en cambio, no existe manera práctica de medir las mismas, por tanto, su cálculo debe realizarse mediante el método analítico que proporciona la norma ANSI/IEEE C57.110 ^[13, ¹⁴, ^15].

El cálculo de las pérdidas se realiza a partir del método analítico de la norma ANSI/IEEE C57.110, partiendo de los valores RMS de los armónicos de las corrientes en ambas mitades del devanado secundario del transformador (w = 2a y w = 2b). El factor de pérdidas armónicas (FHL) se establece como un factor de proporcionalidad aplicado a las pérdidas en condiciones de distorsión armónica y representa la relación entre las pérdidas del transformador con armónicos y estas pérdidas en condiciones nominales o que se tendrían en condiciones nominales y con corrientes sinusoidales ^[16, ¹⁷, ^18], ^21]. Por definición, el factor de pérdidas armónicas se expresa mediante la ecuación (9).

(9)

Donde:

FHL	es el factor de pérdidas armónicas
pH	son las pérdidas en presencia de armónicos
pn	son las pérdidas nominales

De esta manera, los factores de pérdidas amónicas para las pérdidas eléctricas, por corrientes de Eddy y de otras pérdidas adicionales, se pueden expresar de acuerdo a las ecuaciones (10, 11, 12), ^[2, ^19]:

Factor de pérdidas eléctricas:

(10)

Factor de pérdidas por corrientes parásitas:

(11)

Factor de pérdidas adicionales:

(12)

Dado que, en los transformadores que suministren servicio a cargas de 120 V monofásicas y de 240 V monofásicas, las corrientes que circulan por ambas mitades del devanando secundario, pueden estar desequilibradas y los factores de pérdidas eléctricas deben promediarse ^[10], quedando las ecuaciones (13, 14, 15):

(13)

(14)

(15)

Las pérdidas con carga en el transformador se determinan mediante la ecuación (16):

(16)

Validación del modelo en un transformador monofásico con derivación central

Para la validación del modelo analítico se ha diseñado un esquema a escala de laboratorio que permita corroborar los valores de pérdidas de un transformador monofásicos con cargas desequilibradas entre sus fases, combinando cargas lineales y no lineales y con distintos estados de cargabilidad. Para ello se diseñaron 5 tareas prácticas:

• Tarea 1: Caracterizar los elementos y poner a punto el esquema.

• Tarea 2: Mantener la carga lineal constante y variar la carga no lineal.

• Tarea 3: Mantener constante la carga no lineal y variar la carga lineal.

• Tarea 4: Procesamiento de las señales y las mediciones de las tareas 2 y 3.

• Tarea 5: Simulación empleando el modelo ajustado y comparación de los resultados.

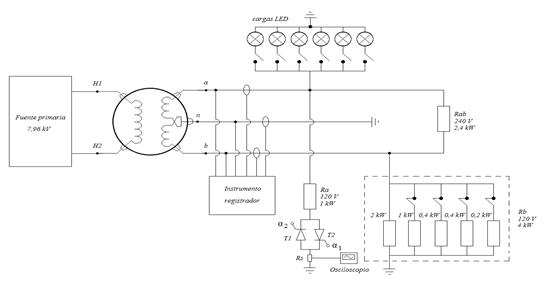
El esquema empleado para la validación experimental del modelo ajustado en un transformador monofásico con derivación central se representa en la figura 2.

Fig. 2 Esquema general para la validación del modelo. Fuente: Elaboración propia 

El listado de materiales necesarios para la implementación del esquema se presenta en la tabla 1.

Tabla 1 Listado de materiales y características. Fuente: Elaboración propia 

No.	Elementos	Cantidad
1	Transformador monofásico de 10 kVA, 7,62/0,12 -0,24 kV	1
2	Resistencia variable de 4 kW.	3
3	Analizador de red Chauvin Arnoux® CA 8331.	1
4	Lámparas LED alumbrado público de 100 W.	5
5	Proyector LED de 150 W.	1
6	Tiristores 20 A.	2
7	Unidad de control para tiristores ANATRONIC.	1
8	Osciloscopio digital RIGOL DS 1000.	1

El transformador a emplear, tiene una potencia nominal de 10 kVA, con tensión nominal 7,62/0,24 kV. En el taller de transformadores, perteneciente a la Empresa Eléctrica de Santiago de Cuba, se realizaron las pruebas de vacío y cortocircuito, con el propósito de determinar los parámetros del circuito equivalente del mismo ^[11].

Desarrollo de las tareas prácticas en el laboratorio

El esquema implementado para la validación práctica aparece detallado en la figura 3. El transformador se carga con una resistencia constante de 2,4 kW a un nivel de tensión de 240V. En la fase a se conectan cargas no lineales variables, entre ellas, 650 W de cargas de alumbrado LED y una carga no constituida por un elemento lineal variable (resistencia de 1 kW), en serie con un control de fase. El control de fase consta de dos interruptores controlados (tiristores) en conexión antiparalelo, a los cuales se les varía el ángulo de disparo en forma simétrica para incrementar o disminuir el nivel de distorsión armónica de la corriente en esta carga. El transformador se carga en la fase b con una resistencia variable de 4 kW, con cinco pasos de 2, 1, 0,4, 0,4 y 0,2 kW respectivamente. En este esquema, las potencias por fase, las corrientes en fase y neutro, así como los espectros de distorsión armónica de las corrientes que serán empleados como variables de entrada en el modelo ajustado son medidos con un analizador de redes (instrumento registrador) en el lado de baja tensión (BT). La potencia por el lado de alta tensión (AT) es medida en el banco de pruebas de transformadores, perteneciente a la Empresa Eléctrica de Santiago de Cuba.

Para la técnica operatoria con el esquema durante el experimento, se procederá de la siguiente manera:

• El contador c marcará las operaciones que se realicen en el circuito (variación del ángulo de disparo, conexión de cargas no lineales o desconexión de pasos de resistencia para variar la carga lineal).

• Entre cada operación transcurrirá un tiempo de 2 min (el analizador realizará 120 registros entre cada operación).

• Con cada operación se debe registrar la hora y la potencia en el primario (lado de AT) del transformador.

• Con cada operación se obtendrán los registros de potencia por fase (lado de BT), el espectro de distorsión armónica de las corrientes en cada fase y el neutro y los valores de THDi empleando el analizador de redes.

• Todas las mediciones se realizarán en un tiempo aproximado de 1 h y 30 min.

Una vez conectado el esquema se energiza el transformador, garantizando tensión nominal en el primario. Antes de iniciar las mediciones deben realizarse las siguientes comprobaciones iniciales:

• Comprobar que los pasos de la carga lineal de la fase a estén en 1 kW / 120 V.

• Comprobar que los pasos de la carga lineal de la fase b estén en 4 kW / 120 V.

• Comprobar que las lámparas LED estén apagadas.

• Ajustar la unidad de control de la carga no lineal con un ángulo cercano a cero, de forma tal que la carga de la fase a sea prácticamente lineal, lo cual se comprueba con el osciloscopio.

Comprobado lo anterior, el esquema está listo para iniciar las mediciones. El esquema de conexión del analizador de redes será una conexión bifásica con neutro, como se presenta en la figura 2. El instrumento será ajustado con un período de muestreo de 1 segundo para registrar armónicos pares e impares hasta el orden 25.

Fig. 3 Esquema operacional para el desarrollo de las tareas prácticas en el laboratorio. Fuente: Elaboración propia 

Para el análisis, se emplearán los datos obtenidos con el analizador de redes en valores intermedios de cada operación en el esquema, descartando los datos en los extremos del intervalo de la operación. Los resultados de las mediciones y el cálculo de las pérdidas totales del transformador serán comparados con los resultados de las simulaciones digitales empleando el modelo ajustado, utilizando el modelo presentado en la figura 4. Con cada simulación se obtendrán todas las magnitudes que caracterizan la operación del transformador en ese estado de carga. Los parámetros para la configuración de las cargas no lineales en el modelo para la simulación digital, se obtienen a partir de los espectros de distorsión armónica individual medidos con el instrumento registrador. Los parámetros para la configuración del transformador en el modelo aparecen detallados en la tabla 3.

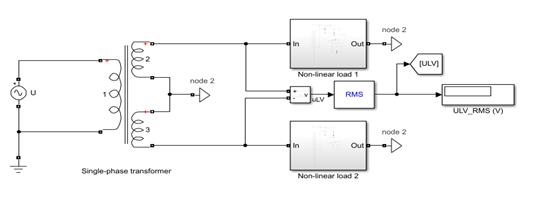
Fig. 4 Esquema para la simulación digital del transformador monofásico empleando el modelo ajustado. Fuente: Elaboración propia 

El ajuste del modelo analítico, para determinar las pérdidas del transformador mediante la simulación digital, cuenta con cuatro subsistemas ^[19, ^20], ellos son:

1. Subsistema Red de Distribución Primaria (RDP).

2. Subsistema del transformador.

3. Subsistema de la carga no lineal.

4. Subsistema para el procesamiento digital de señales, cálculo del punto de operación y presentación de los resultados.

El subsistema de la RDP se crea a partir de señales puramente sinusoidales, con nivel de tensión nominal de fase de 7,62 kV y frecuencia constante de 60 Hz. En el subsistema del transformador se emplea como parámetros para la configuración el modelo del circuito equivalente de Steinmetz del transformador en una fase ^[19]. Con este subsistema se persigue obtener las tensiones y corrientes en cada uno de los devanados del transformador para su posterior procesamiento digital. Los parámetros del circuito de Steinmetz se calculan a partir de las pruebas de vacío y cortocircuito (ver tabla 3). La carga no lineal se caracteriza a partir de las mediciones de corriente de carga, que se realizan en los alimentadores empleando el instrumento registrador. Por último, el procesamiento digital de las señales discretas, persigue determinar valores característicos de las tensiones y las corrientes en los devanados del transformador y el espectro de distorsión armónica de amplitud y de fase de las corrientes en los devanados para ser empleado en la estimación de las pérdidas de acuerdo al modelo ajustado propuesto.

Resultados y discusión

En el proceso de validación del modelo con el esquema para determinar las pérdidas de transformación se realizaron 30 operaciones, garantizando de esta manera la operación del transformador en distintos estados de carga y con diferentes valores de distorsión armónica (tareas 2 y 3 del experimento). La ejecución de las operaciones se realizó siguiendo el esquema presentado en la figura 4. En la tabla 2, se resumen los resultados de las mediciones realizadas en el laboratorio para la determinación de las pérdidas del transformador en cada estado de carga. Los valores de pérdidas de transformación medidas en el laboratorio se determinan mediante la ecuación (17).

(17)

Donde:

P1	es la potencia medida en el banco de pruebas de transformadores, por el lado de alta tensión en el transformador de 10 kVA
P2	es la potencia medida con el instrumento registrador por el lado de baja tensión, la cual se obtiene a partir de las potencias en cada una de las fases del transformador, de acuerdo con la ecuación (18), de la forma:

(18)

Tabla 2 Resultados de las pruebas en laboratorio. Fuente: Elaboración propia 

Fecha	Hora	Operación (c)	P1 (W)	Pa (W)	Pb (W)	P2 (W)	pTmedido(W)
17/05/2024	9:49	1	6684,59	1964,61	4507,53	6472,20	212,39
17/05/2024	9:50	2	7189,13	2102,38	4864,77	6967,10	222,03
17/05/2024	9:51	3	7097,92	2034,17	4852,32	6886,53	211,39
17/05/2024	9:52	4	7028,82	1963,37	4844,88	6808,22	220,60
17/05/2024	9:53	5	6897,26	1822,80	4859,68	6682,50	214,76
17/05/2024	9:54	6	6553,38	1487,13	4863,45	6350,58	202,79
17/05/2024	9:55	7	6443,51	1355,18	4886,13	6241,32	202,19
17/05/2024	9:56	8	6556,75	1448,60	4900,37	6348,80	207,95
17/05/2024	9:57	9	6631,90	1529,97	4888,77	6418,63	213,27
17/05/2024	9:58	10	6703,32	1621,67	4866,85	6488,48	214,83
17/05/2024	9:59	11	6798,10	1716,58	4874,33	6590,95	207,15
17/05/2024	10:00	12	6930,51	1846,10	4864,45	6710,62	219,90
17/05/2024	10:01	13	6987,22	1927,63	4838,78	6766,37	220,86
17/05/2024	10:02	14	6722,41	1935,95	4579,27	6515,25	207,16
17/05/2024	10:03	15	6351,72	1948,97	4202,40	6151,38	200,34
17/05/2024	10:04	16	2017,55	1841,24	1841,24	1841,24	176,31
17/05/2024	10:05	17	5216,39	1940,67	3107,78	5048,55	167,84
17/05/2024	10:06	18	5134,70	1849,02	3114,92	4963,90	170,80
17/05/2024	10:07	19	5046,16	1757,08	3121,63	4878,73	167,42
17/05/2024	10:08	20	4837,62	1624,08	3047,95	4671,97	165,65
17/05/2024	10:09	21	4925,83	1610,75	3151,82	4762,58	163,25
17/05/2024	10:10	22	4954,84	1621,25	3174,57	4795,82	159,02
17/05/2024	10:11	23	5255,06	1905,93	3177,55	5083,49	171,57
17/05/2024	10:12	24	4734,72	1392,33	3179,90	4572,28	162,43
17/05/2024	10:13	25	4911,96	1591,48	3155,25	4746,73	165,23
17/05/2024	10:14	26	5136,74	1839,68	3127,55	4967,22	169,52
17/05/2024	10:15	27	5397,46	2105,55	3119,13	5224,67	172,79
17/05/2024	10:16	28	5498,67	2207,42	3120,85	5328,27	170,40
17/05/2024	10:17	29	5610,49	2215,37	3220,60	5436,03	174,46
17/05/2024	10:18	30	5997,39	2190,37	3626,05	5816,42	180,97

En la figura 5, se presentan de forma gráfica los valores de las pérdidas obtenidas a partir de las mediciones, el THDipromedio del lado de BTy la cargabilidad del transformador en porciento, para el caso de estudio a escala de laboratorio.

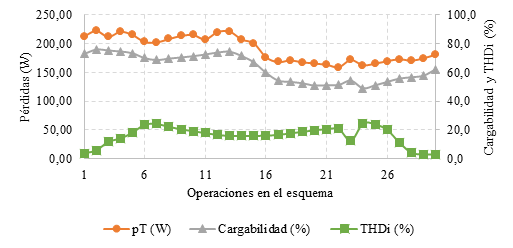
Fig. 5 Gráfico de pérdidas totales contra el valor de THDi obtenidos en las pruebas del transformador de 10kVA a escala de laboratorio. Fuente: Elaboración propia 

Como se observa en la figura 5, se incrementa la distorsión armónica en la fase b como el incremento del ángulo de disparo de los tiristores en la carga no lineal. En cambio, tanto la cargabilidad como las pérdidas en el transformador tienen una tendencia a disminuir por la consiguiente disminución del valor eficaz de la corriente de fase en esa carga. Entre las operaciones 7 y 13 se incrementa la carga en la fase a con el alumbrado LED. Aunque estas cargas son no lineales, su incorporación contribuye a que la forma de onda de la corriente de carga en esa fase se aproxime más a una sinusoide, incrementándose el valor del armónico fundamental de la corriente y, por tanto, reduciendo el valor THDi. En este intervalo, las pérdidas se incrementan, conforme aumenta el valor RMS de la corriente de carga. A partir de la operación número 16, comienza a retirarse del esquema carga lineal en la fase b, haciendo que la componente no lineal de la fase a sea mayor y su efecto más notable en las pérdidas totales. A partir de la operación 25, se varía nuevamente el ángulo de disparo de los tiristores reduciendo el valor de la distorsión armónica, incrementando el valor RMS de la corriente de carga en fase a y aumentando ligeramente la cargabilidad del transformador.

Para comparar estos resultados prácticos con los valores obtenidos en las simulaciones se han empleado los valores de distorsión armónica individual obtenidos con el analizador de redes conectado en el secundario para cada una de las operaciones realizadas. En la tabla 3, se resumen los resultados de las pérdidas con carga y las pérdidas de transformación para cada una de las simulaciones realizadas.

Tabla 3 Resultados de la simulación en Matlab con el modelo ajustado. Fuente: Elaboración propia 

Fecha	Hora	Operación (c)	pTmodelo (W)	pELEC(W)	pED(W)	pAD(W)
17/05/2024	9:49	1	207,53	111,20	19,20	9,32
17/05/2024	9:50	2	215,02	115,97	21,08	10,17
17/05/2024	9:51	3	214,76	115,10	21,75	10,11
17/05/2024	9:52	4	213,79	114,10	21,86	10,03
17/05/2024	9:53	5	212,16	112,27	22,16	9,93
17/05/2024	9:54	6	206,33	107,24	21,71	9,58
17/05/2024	9:55	7	203,79	105,14	21,39	9,46
17/05/2024	9:56	8	205,60	106,68	21,55	9,58
17/05/2024	9:57	9	206,91	107,87	21,60	9,64
17/05/2024	9:58	10	208,38	109,18	21,70	9,70
17/05/2024	9:59	11	210,65	110,96	22,03	9,86
17/05/2024	10:00	12	213,21	113,04	22,36	10,02
17/05/2024	10:01	13	214,11	113,90	22,38	10,03
17/05/2024	10:02	14	206,47	109,20	20,40	9,07
17/05/2024	10:03	15	195,82	102,47	17,77	7,78
17/05/2024	10:04	16	178,92	91,28	13,93	5,91
17/05/2024	10:05	17	167,08	82,91	11,60	4,77
17/05/2024	10:06	18	165,34	81,48	11,41	4,65
17/05/2024	10:07	19	163,61	80,06	11,21	4,54
17/05/2024	10:08	20	160,41	77,59	10,70	4,32
17/05/2024	10:09	21	161,08	77,96	10,92	4,41
17/05/2024	10:10	22	161,48	78,23	11,01	4,44
17/05/2024	10:11	23	165,94	82,75	10,64	4,76
17/05/2024	10:12	24	157,40	74,77	10,61	4,22
17/05/2024	10:13	25	161,56	78,00	11,32	4,43
17/05/2024	10:14	26	165,65	81,53	11,64	4,68
17/05/2024	10:15	27	168,65	84,95	10,99	4,91
17/05/2024	10:16	28	169,36	86,25	10,32	4,99
17/05/2024	10:17	29	171,75	88,01	10,73	5,21
17/05/2024	10:18	30	181,62	94,83	12,78	6,21

En la figura 6, se representan las pérdidas con carga del transformador de 10 kVA obtenidas mediante la simulación digital.

Fig. 6 Valores de las pérdidas con carga, distorsión armónica y cargabilidad del transformador de 10 kVA obtenidos en la simulación digital. Fuente: Elaboración propia 

A partir de las pérdidas totales obtenidas mediante la simulación empleando el modelo ajustado y las pérdidas determinadas mediante las pruebas (ver figuras 5 y 6), es posible comparar ambos resultados y determinar el valor de la diferencia absoluta de las pérdidas totales, que para este análisis se determina por la ecuación (19):

(19)

Donde:

yi	es el valor objetivo, obtenido mediante la prueba en el laboratorio (pTmedido)
xi	es el valor predicho, obtenido mediante la simulación digital (pTmodelo)

El porcentaje de diferencia para estos valores puede calcularse a partir de la diferencia absoluta de las pérdidas totales según la ecuación (20).

(20)

En la tabla 4, se resumen los resultados de este análisis para cada una de las operaciones realizadas en el esquema.

Tabla 4 Comparativa entre los valores de pérdidas totales obtenidos a partir de las mediciones con los valores resultantes de la simulación con el modelo ajustado. Fuente: Elaboración propia 

Operación (c)	pTmedido(W)	pTmodelo(W)	ΔpT(W)	ξp (%)
1	212,39	207,53	4,86	2,3
2	222,03	215,02	7,01	3,2
3	211,39	214,76	3,37	1,6
4	220,60	213,79	6,81	3,1
5	214,76	212,16	2,59	1,2
6	202,79	206,33	3,54	1,7
7	202,19	203,79	1,60	0,8
8	207,95	205,60	2,35	1,1
9	213,27	206,91	6,36	3,0
10	214,83	208,38	6,45	3,0
11	207,15	210,65	3,50	1,7
12	219,90	213,21	6,68	3,1
13	220,86	214,11	6,75	3,1
14	207,16	206,47	0,69	0,3
15	200,34	195,82	4,51	2,3
16	176,31	178,92	2,61	1,5
17	167,84	167,08	0,76	0,5
18	170,80	165,34	5,47	3,3
19	167,42	163,61	3,82	2,3
20	165,65	160,41	5,24	3,2
21	163,25	161,08	2,17	1,3
22	159,02	161,48	2,46	1,5
23	171,57	165,94	5,62	3,3
24	162,43	157,40	5,03	3,1
25	165,23	161,56	3,67	2,2
26	169,52	165,65	3,87	2,3
27	172,79	168,65	4,15	2,4
28	170,40	169,36	1,04	0,6
29	174,46	171,75	2,71	1,6
30	180,97	181,62	0,66	0,4

El mayor valor de las diferencias absolutas entre los resultados de las pérdidas (ξp) se obtiene para un THDi del 3,3 % correspondiente con la operación 23 en la cual se registró la mayor variación en la carga del transformador. Los valores de porcentaje de diferencia no exceden el 5 % en ninguno de los casos estudiados. A partir de esta comparación es posible calcular el porciento de diferencia entre estos valores de pérdidas, así como el error absoluto medio (MAE) del análisis. El MAE proporciona el valor promedio de la diferencia absoluta entre el valor de la predicción y el valor objetivo en un número n de observaciones o pruebas ^[21]. Este valor puede determinarse de acuerdo a la ecuación (21):

(21)

El valor del MAE para los valores que se muestran en la tabla 6 es de 2,04 W, el cual representa el 1,02 % de las pérdidas nominales de este transformador. Este valor de error absoluto medio refleja que existe una buena correlación entre ambos resultados.

Conclusiones

El modelo fue validado para un transformador monofásico con derivación central y para distintos estados de carga, obteniéndose que los valores de porcentaje de diferencia entre las pérdidas calculadas y las medidas en el laboratorio no exceden el 5 % en ninguna de las pruebas realizadas, arrojando un error absoluto medio de 2,04 W, reflejando que existe una buena correlación entre ambos resultados. Dado que las corrientes en las fases son distintas en su amplitud y forma de onda, el método analítico de la Norma ANSI/IEEE Std. C57.110 no puede ser directamente aplicado, por lo que es ajustado para trabajar con los factores de pérdidas promedio, a partir del procesamiento de las corrientes en los devanados obtenidas por medio de la simulación digital.

Los resultados obtenidos en este experimento son prometedores y pudieran justificar la aplicación del modelo obtenido, tanto a transformadores monofásicos, como a bancos trifásicos de transformadores monofásicos con distintos esquemas de conexión, lo cual constituye un resultado importante en nuestro país, considerando la amplia presencia de estos bancos en las redes de distribución.

Referencias

1.  Chattopadhyay, S; Mitra, M; and Sengupta, S. “Electric Power Quality,” in Electric Power Quality,. Chattopadhyay, S; Mitra, M; and Sengupta, S Eds., in PowerSystems. , Dordrecht: Springer Netherlands, 2011, p. 5-12. DOI 10.1007/978-94-007-0635-4_2. ISBN 978-94-007-0635-4. Disponible en: https://link.springer.com/chapter/10.1007/978-94-007-0635-4_21.

2.  Aziz, M. H. A; et al. “A review on harmonic mitigation method for non-linear load in electrical power system,” AIP Conf. Proc., May 2021, vol. 2339, n. 1, p. 020-022 , DOI 10.1063/5.0044251. ISSN 1551-7616. Disponible en: https://pubs.aip.org/aip/acp/article-abstract/2339/1/020022/1027837/A-review-on-harmonic-mitigation-method-for-non?redirectedFrom=fulltext2.

3.  Abbas, A. S; et al., “Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation,” Appl. Sci. Jan. 2021, vol. 11, n. 2, DOI 10.3390/app11020774. ISSN 2076-3417. Disponible en: https://www.mdpi.com/2076-3417/11/2/7743.

4.  González, J. E. C; et al. “Efectos de los armónicos de corriente en las pérdidas de transformadores de distribución monofásicos/Effects of Current harmonics on the distribution single-phase transformers losses,” Ing. Energética. Apr. 2019, vol. 40, n. 2, p. 112-127. ISSN 1815-5901. Disponible en: https://rie.cujae.edu.cu/index.php/RIE/article/view/561/6304.

5.  Gómez-Sarduy, J; et al. “Influencia de los armónicos de corriente sobre las pérdidas en los transformadores de distribución monofásicos con derivación central,”. El hombre y la máquina. 2014, n. 45, p. 33-43. ISSN 0121-0777. Disponible en: https://www.redalyc.org/pdf/478/47838946005.pdf5.

6.  El-Ela, A. A; et al. “Harmonic Mitigation by Optimal Allocation of Tuned Passive Filter in Distribution System,” Energy Power Eng. Jul. 2022, vol. 14, n. 7, DOI 10.4236/epe.2022.147016. ISSN 1947-3818. Disponible en: https://www.scirp.org/journal/paperinformation?paperid=1189806.

7.  Solanki, A. Y;Vyas, D. S. R “A Review on Power Quality Enhancement Using Custom Power Devices,”. International Research Journal of Engineering and Technology (IRJET). 2021, vol. 8, n. 2, p. 287-290. ISSN 2395-0056. Disponible en: https://www.irjet.net/archives/V8/i2/IRJET-V8I254.pdf7.

8.  Wadhawan, J; et al. “A Review on Power Quality Problems and Improvement Techniques,” Int. J. Eng. Res., 2020, vol. 8, n. 10. ISBN 978-1-5090-5682-8. Disponible en: https://ieeexplore.ieee.org/document/82448828.

9.  IEEE C57.110-2018 “IEEE Recommended Practice for Establishing Liquid-Immersed and Dry-Type Power and Distribution Transformer Capability When Supplying Non sinusoidal Load Currents,” IEEE Std C57110TM-2018 Revis. IEEE Std C57110-2008, p. 1-68, Oct. 2018, DOI 10.1109/IEEESTD.2018.8511103. Disponible en: https://www.en-standard.eu/ieee-c57-110-2018-ieee-recommended-practice-for-establishing-liquid-immersed-and-dry-type-power-and-distribution-transformer-capability-when-supplying-nonsinusoidal-load-currents-2/9.

10.  Pejovski, D; et al. “Impact of different harmonic loads on distribution transformers,” Procedia Eng., Jan. 2017, vol. 202, p. 76-87, DOI 10.1016/j.proeng.2017.09.696. ISSN 1877-7058. Disponible en: https://www.sciencedirect.com/science/article/pii/S187770581734235210.

11.  Bocanegra, S. Y; et al. “Estimación de parámetros en transformadores monofásicos empleando medidas de tensión y corriente,” Rev. UIS Ing., 2020, vol. 19, n. 4, p. 63-75, ISSN 2145-8456. Disponible en: https://revistas.uis.edu.co/index.php/revistauisingenierias/article/view/1088011.

12.  IEC 61000-2-2:2002. “Electromagnetic compatibility (EMC) - Part 2-2: Environment - Compatibility levels for low-frequency conducted disturbances and signalling in public low-voltage power supply systems” 2002 Disponible en: https://webstore.iec.ch/publication/413312.

13.  Cervantes Yanami, B. A; “Programa de cálculo para la velocidad de envejecimiento de los transformadores convencionales en el sector de distribución típico 1, Miraflores,” Trabajo para optar por el título de Ingeniero Electricista. Univ. Nac. Mayor San Marcos, 2022. Disponible en: https://cybertesis.unmsm.edu.pe/handle/20.500.12672/1776113.

14.  León-Martínez, V; et al. “Load Losses and Short-Circuit Resistances of Distribution Transformers Accordingto IEEE Standard C57.110,” Inventions, Dec. 2023, vol. 8, n. 6, DOI 10.3390/inventions8060154. ISSN 2411-5134. Disponible en: https://www.mdpi.com/2411-5134/8/6/15414.

15.  León-Martínez, V; et al. “Assessment of Load Losses Caused by Harmonic Currents in Distribution Transformers UsingtheTransformer Loss Calculator Software,” Environments, Oct. 2023, vol. 10, n. 10, DOI 10.3390/environments10100177. ISSN 2076-3298. Disponible en: https://www.mdpi.com/2076-3298/10/10/17715.

16.  Yazdani-Asrami, M; et al. “No-load loss calculation of distribution transformers supplied by non sinusoidal voltage using three-dimensional finite element analysis,” Energy. Feb. 2013, vol. 50, p. 205-219, DOI 10.1016/j.energy.2012.09.050. ISSN 1873-6785. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S036054421200729316.

17.  Arghandeh, R; Onen, A; Jung, J; Broadwater, R. P “Harmonic interactions of multiple distributed energy resources in power distribution networks,” Electr. PowerSyst. Res. Dec. 2013, vol. 105, p. 124-133, DOI 10.1016/j.epsr.2013.07.018. ISSN 1873-2046. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S037877961300199517.

18.  Maan, J. S; Singh S; Singh, A, “Impact of Harmonics on Power Transformer Losses and Capacity Using Open DSS,” Int. J. Emerg. Electr. PowerSyst. Aug. 2019, vol. 20, n. 4, DOI 10.1515/ijeeps-2018-0349. ISSN 2194-5756. Disponible en: https://www.degruyter.com/document/doi/10.1515/ijeeps-2018-0349/html?lang=en18.

19.  Grau Merconchini, F; et al. “Modelo para simular el efecto de la distorsión armónica en las pérdidas de transformadores monofásicos,”. Ingeniería Energética. Aug. 2023, vol 44, n. 2, e3206. ISSN 1815-5901. Disponible en: https://rie.cujae.edu.cu/index.php/RIE/article/view/855/91219.

20.  Khorasani, P. G; Deihimi, A. “A new modelingof Matlab transformerforaccuratesimulationofferroresonance,” 2009 Int. Conf. Power Eng. Energy Electr. Drives, pp. 529-534, Mar. 2009, doi: 10.1109/POWERENG.2009.4915249

21.  Gómez, J. M. A; et al. “Estimación del factor K en transformadores de distribución usando modelos de regresión lineal,”. TECNURA. 2016, vol. 20, n. 48, p. 29-40. ISSN 0123-921X. Disponible en: https://www.redalyc.org/pdf/2570/257046835003.pdf21.

Recibido: 25 de Mayo de 2024; Aprobado: 02 de Julio de 2024

^* Autor de la correspondencia: [e-mail]

Los autores declaran que no existe conflicto de intereses.

Frank Grau Merconchini: Participó en el diseño de la investigación, diseño del modelo, la simulación, el procesamiento de los datos y la redacción del manuscrito, la revisión crítica de su contenido y en la aprobación final.

Orestes Hernández Areu: Participó en el diseño de la investigación, diseño del modelo y la redacción del manuscrito, la revisión crítica de su contenido y en la aprobación final.

Eduardo López Pérez: Participó en el diseño del modelo y el procesamiento de los datos, la revisión crítica de su contenido y en la aprobación final.

Nelson Alexey Castro Torres: Participó en el diseño del modelo y la simulación, la revisión crítica de su contenido y en la aprobación final.