Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Electrónica, Automática y Comunicaciones
versión On-line ISSN 1815-5928
EAC vol.36 no.3 La Habana sep.-dic. 2015
ARTÍCULO ORIGINAL
Modelación matemática para el control de la postcombustión en un horno de reducción de níquel
Mathematical modeling for postcombustion control in a nickel reduction oven
Ing. Deynier Montero Góngora, I Dr. C. Mercedes Ramírez Mendoza, II MSc. Amauris Gilbert Hernández, I Ing. Sergio Campos PerdicesIII
I Instituto Superior Minero Metalúrgico de Moa (ISMMM), Holguín, Cuba
II Universidad de Oriente (ISPJAM), Santiago de Cuba, Cuba
III Empresa Comandante Ernesto Ché Guevara, Holguín, Cuba
RESUMEN
Se realizó la identificación experimental del subproceso de postcombustión de un horno de múltiples hogares, destinado a la reducción de níquel mediante el esquema carbonato-amoniacal. Se realizaron varios experimentos en diferentes puntos de operación del proceso, atendiendo al carácter no lineal del mismo y utilizando como señal de excitación una Secuencia Binaria Pseudoaleatoria de Amplitud Modulada. Se obtuvieron los modelos matemáticos aproximados de la concentración de monóxido de carbono residual, la temperatura en los hogares 4 y 6 ante cambios en el flujo de aire correspondiente a estos hogares y variaciones en el flujo de mineral como variable perturbadora del subproceso. Se realizó la validación de los modelos obtenidos Error de salida, Autorregresivo con entrada exógena; los cuales brindaron ajustes de 63 a 84 % y además se apreció un comportamiento aceptable de los residuos. Los modelos se utilizaron para el diseño de un algoritmo de control de la temperatura en los hogares 4 y 6, lo cual influye decisivamente sobre la estabilidad del perfil de temperatura del horno. Se empleó como herramienta de cálculo el programa MATLAB.
Palabras claves: Modelación matemática, postcombustión, reducción, identificación de sistemas, mineral, control
ABSTRACT
The experimental identification of the postcombustion subprocess in a multiple home furnace, destined for nickel reduction by the carbonate-ammonia was carried out. Several experiments at different operating points of the process were performed, taking into account its nonlinear nature and using a width modulated pseudo random binary sequence as excitation signal. As a result, it was obtained the approximate mathematical models of the concentration of monoxide carbon residual, the temperature in 4 and 6 households before changes in air flow corresponding to these homes and the variations in mineral flow as disturbing variable in the subprocess. The validation of the obtained models Output-Error, Auto Regressive Exogenous with input was made; which provided adjustments from 63 to 84 % and also an acceptable behavior of residues was observed. The models were used to design an algorithm for temperature control in 4 and 6 houses, which have a decisive influence on the stability of the oven temperature profile. MATLAB as tool calculation was used. Keywords: experimental identification, postcombustion, reduction, identification system, mineral, control
INTRODUCCIÓN
La automatización como proceso ha sido una de las mayores creaciones del hombre, pues a partir de sus resultados se han logrado disminuir significativamente fallas de tipo humano, así como se han mejorado los niveles de producción y sus propios niveles de vida. El control automático desempeña una función vital en el avance de la ingeniería y la ciencia, siendo una parte importante e integral de los procesos modernos. Es esencial dentro de las operaciones industriales en el control de variables como: presión, temperatura, humedad, viscosidad y flujo.
En las plantas niquelíferas en las que se utiliza la tecnología de lixiviación carbonatoamoniacal, también conocida universalmente como proceso «Caron», se emplea el horno de soleras múltiples 1, el cual se destina a la reducción selectiva de los óxidos de níquel y cobalto a sus correspondientes formas metálicas, que los hace aptos para la lixiviación carbonato-amoniacal. Esta tecnología resulta adecuada para procesar minerales serpentínicos y lateríticos, pero durante la reducción se producen pérdidas notables debido a la formación de estructuras cristalinas de espinelas de hierro, olivinos y piroxenos que atrapan al níquel y al cobalto en forma de óxidos y en menor grado en estado metálico, y a la aparición de altos contenidos de hierro metálico en el mineral reducido, lo que trae como consecuencia que disminuya la extracción de níquel y cobalto en el proceso de lixiviación 2. Estas pérdidas se incrementan cuando se viola el perfil de temperatura y/o el perfil gaseoso dentro del horno de reducción, de ahí la importancia del control de la temperatura en el mismo.
Para diseñar una estrategia de control automático que garantice las demandas existentes se debe tener en cuenta el comportamiento de la temperatura en función del flujo de aire de postcombustión en estado estacionario 3, así como disponer de un modelo matemático que describa la dinámica del proceso.4
En relación con el tema resultan interesantes los trabajos desarrollados en 5, donde se obtuvieron modelos matemáticos para los hornos de la Empresa René Ramos Latour de Nicaro que poseían características similares, sin embargo operaban bajo diferentes condiciones de explotación. También en 6 se obtuvieron modelos por la vía de la identificación experimental para los hornos de la Empresa Che Guevara (objeto de estudio), presentando el inconveniente de no disponer de las condiciones técnicas adecuadas para el proceso de reducción de mineral. De manera que los modelos presentan restricciones para las condiciones normales de operación. Se considera como principal limitación de estos trabajos que, a pesar de proponer los modelos no presentan la estrategia de control para la temperatura de los hogares.
Ante este problema, el presente trabajo tiene como objetivo la obtención de un modelo matemático mediante la aplicación de técnicas de identificación experimental, el cual se utilizará en el diseño de un algoritmo de control automático para el subproceso de postcombustión que ocurre en el horno de reducción. El control de la postcombustión está vinculado directamente con el control de la temperatura de los hogares 4 y 6, lo que es de primordial importancia para el logro de una mayor eficiencia en el funcionamiento del horno y para la disminución de la contaminación ambiental.
Breve descripción del proceso de reducción de níquel
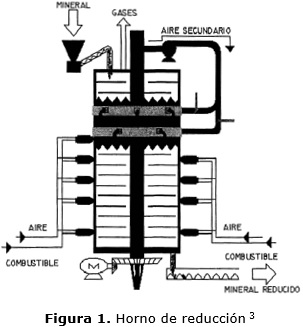
El proceso que se realiza en la planta Hornos de Reducción, debe garantizar la reducción del óxido de níquel a níquel metálico, haciéndolo apto para la lixiviación amoniacal. Para ello la planta cuenta con 24 hornos, cada uno compuesto por 17 hogares, enumerados de arriba hacia abajo desde el 0 hasta el 16; el mismo consiste en un cilindro metálico de 23,5 m de altura y 6,8 m de diámetro (figura 1).7
La mezcla de minerales antes de ser sometida al proceso de reducción, se somete a un proceso de secado y molienda en la planta de Preparación del Mineral.
Seguidamente, es homogenizada y almacenada en los silos, para posteriormente ser bombeada hacia las tolvas de los hornos. Luego, pasa a los dosificadores de pesaje automático, que son los equipos encargados de garantizar una alimentación uniforme al horno, de acuerdo a la productividad fijada. Después, el mineral es transportado al hogar 0 del horno a través del sinfín alimentador.
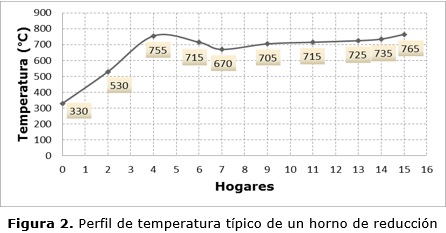
La mezcla de minerales una vez dentro del horno, es sometida a un proceso de reducción selectiva, que se logra estableciendo cierto perfil de temperatura dentro del mismo (figura 2) y una concentración determinada de gases reductores (CO+H2), para ello el horno dispone de 10 cámaras donde se desarrolla la combustión fundamental con quemadores de alta presión para quemar de forma incompleta el petróleo, las cuales además de garantizar el perfil de temperatura requerido enriquecen la atmósfera reductora. El tiempo de retención del mineral en el horno es de aproximadamente 45 minutos.
En estas condiciones es posible el desarrollo de las reacciones de reducción (1, 2, 3), que dependen de un conjunto de variables y parámetros cuya interacción en el proceso tecnológico, determina los valores de la cantidad de níquel extractable como principal indicador de calidad. 8
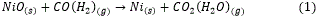
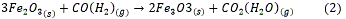
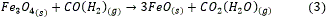
En los hogares 4 y 6 del horno se produce una postcombustión consistente en suministrar aire secundario con un doble propósito: el primero de carácter económico, pues los efectos exotérmicos de las reacciones de combustión de los agentes reductores, producen una disminución del consumo de petróleo y se aprovecha su contenido calórico.
El segundo motivo es de carácter social y económico, pues los gases que salen del horno al ponerse en contacto con las chispas que se producen frecuentemente en los electrofiltros por efecto electromagnético, pueden producir explosiones, de manera que cuando se detectan valores de la concentración de CO y H2 por encima de los límites permisibles, se les da salida a los gases directamente a la atmósfera con las consiguientes pérdidas por arrastre y contaminación ambiental asociada.
Los fenómenos físico químicos que tienen lugar en los hogares 4 y 6 son relativamente complicados, si se tienen en cuenta los fenómenos de transferencia de calor y la naturaleza de los minerales presentes. En estos hogares se han implementado con anterioridad lazos de control independientes para las temperaturas, los cuales han entrado en conflicto debido a que en ambos se manipula el flujo de aire, proveniente de un mismo conducto que se bifurca en dos ramas.
Variables del subproceso de postcombustión
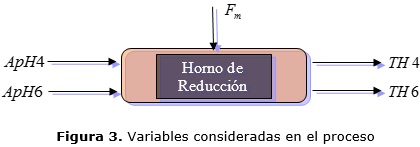
El problema de control a ser resuelto se presenta de la siguiente forma: existen dos variables de entrada y dos de salida, más una perturbación (Figura 3). Las variables a manipular son las aperturas de las válvulas reguladoras de flujo de aire a los hogares 4 y 6 (ApH4, ApH6). Las variables a controlar (controladas o de salida) son las temperaturas de los hogares 4 y 6 (TH4, TH6), mientras que la perturbación considerada es el flujo de mineral alimentado al horno (Fm).
Obtención de un modelo aproximado del proceso mediante la identificación experimental
La obtención de un modelo matemático que describa el proceso desde el punto de vista fenomenológico sería en extremo complicada, pues los procesos físico químicos involucrados conducirían a sistemas de ecuaciones diferenciales en derivadas parciales, consecuentemente no lineales y variables en el tiempo, por ello se optó por la identificación experimental para obtener modelos aproximados para diferentes puntos de operación. 9 ,10
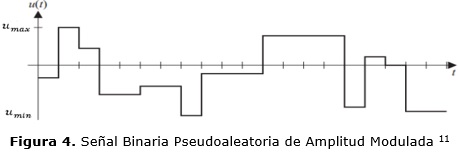
Como señal de entrada para excitar al proceso se utilizaron señales binarias pseudoaleatorias de amplitud modulada (APRBS) (Figura 4) con la intención de que los datos obtenidos puedan usarse tanto para obtener modelos lineales, como modelos no lineales que permitan diseñar y probar estrategias de control avanzado. En esta señal no solo se modula la frecuencia de excitación, como es el caso de las señales binarias pseudoaleatorias (PRBS), sino también la amplitud, y cubre un rango de frecuencias mayor que la PRBS, aunque existen más parámetros de diseño a tomar en cuenta tales como el rango y la distribución de amplitudes de la señal de entrada. 11
En este caso al diseño clásico de una PRBS siguiendo el criterio ofrecido en 12 se añadió un generador de números aleatorios para seleccionar valores de amplitud en el rango de umin a umax. Aunque la distribución de amplitudes y frecuencias de la señal de prueba resultante no está igualmente distribuida sobre el rango completo de operación, esto no representa un problema para una secuencia de prueba de suficiente longitud.
Diseño del experimento
El trabajo se desarrolló en la planta Hornos de Reducción de la empresa niquelífera Comandante Ernesto Ché Guevara de Moa. Los experimentos se realizaron en el horno 5 que cuenta con adecuadas condiciones técnicas y posee una mayor sensibilidad en la respuesta de las temperaturas de H4 y H6 ante variaciones en las aperturas de las válvulas de regulación. El horno posee 7 cámaras de combustión (6S, 8N, 8S, 10N, 10S, 12N, 12S y 15S), consta de 67 brazos en el eje central y todas las bóvedas poseen buen estado técnico.
Para los experimentos con el flujo de aire se generó primero una PRBS de quinto orden con un período de conmutación de 1 minuto escogido a partir de las curvas de reacción de TH4 y TH6. Se tomó un período de muestreo de 3 segundos. Luego se generó una secuencia de valores aleatorios con la ayuda del comando rand del MATLAB, en el rango de amplitud de la aperturas de las válvulas de H4 y H6, los cuales se añadieron a los estados de la secuencia binaria pseudoaleatoria antes generada. Esta amplitud se tomó teniendo en cuenta el intervalo típico en que trabajan dichas válvulas. Bajo estas consideraciones se obtuvo una señal modulada en amplitud y frecuencia.
Para los experimentos con el flujo de mineral se generó primero una PRBS de tercer orden, con un período de conmutación de 5 minutos procediendo de manera similar al caso anterior. Luego se generó una secuencia de valores aleatorios en el rango de amplitud en que trabaja el dispositivo de pesaje, los cuales se añadieron a los estados de la secuencia binaria pseudoaleatoria antes generada. Esta amplitud se tomó teniendo en cuenta el intervalo típico de la carga del horno.
Para el proceso de identificación, se realizó un tratamiento previo de los datos. Esto consistió en suprimir los niveles constantes y hacer que la media de los mismos fuera cero. Después se hizo el filtrado siguiendo las recomendaciones realizadas en 13. Se seleccionó un grupo de datos para estimar el modelo y otra parte para validarlo.
Para el procesamiento de los datos se utilizó la caja de herramientas de Identificación de sistemas del paquete de programas MATLAB, 14, mientras que para la recopilación de datos durante los experimentos realizados con el fin de identificar el proceso, se utilizaron los sistemas de supervisión y control (CITECT y EROS), los cuales permiten la medición de todas las variables de interés para el estudio y análisis del subproceso de postcombustión.
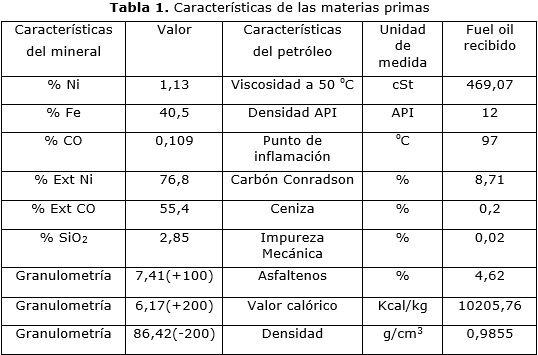
La composición química de la materia prima influye directamente en los resultados de la reducción. Atendiendo a esto se fijan las temperaturas del horno o régimen de calentamiento del mineral. La composición química del mineral y las características del petróleo suministrado a la Planta «Hornos de Reducción» durante la realización de los experimentos se muestran en la Tabla 1, siendo sus parámetros típicos durante el año.
Resultados y discusión
En la figura 5 se observa el gráfico temporal obtenido al aplicar una APRBS sobre la apertura de la válvula reguladora de flujo de aire H4 (ApH4), en el rango de 12 a 57 % con apertura constante de la válvula de H6 en 40 % y con un flujo de mineral alimentado al horno de 18,2 tn/h. En la parte superior se muestra el comportamiento de las variables de salida (TH6, TH4).
En la figura 6 se observa el gráfico temporal obtenido al variar de 20 a 68 % la apertura de la válvula reguladora de flujo de aire H6 (ApH6). El horno se encontraba operando con un flujo de mineral de 18,2 tn/h y la apertura de la válvula de H4 se mantuvo constante en 25 %. En la parte superior de la figura se muestra el comportamiento de las variables de salida (TH4, TH6), siendo evidente el comportamiento decreciente de TH4 e inversamente proporcional a TH6 debido a la interacción existente entre estas variables.
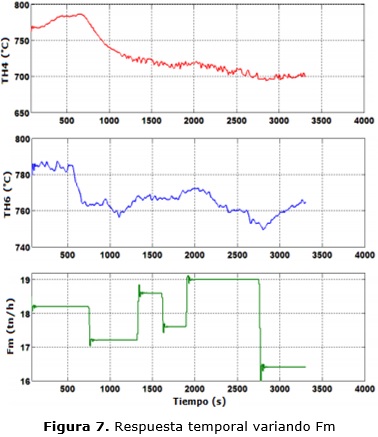
En la figura 7 se observan los resultados de las variables de entrada y salida obtenidos tras experimentar con flujos de 16 a 19 tn/h, mientras que las aperturas de las válvulas reguladoras de flujo de aire en H4 y H6 se mantuvieron constantes en 20 y 30 % respectivamente. Se determinaron modelos de una entrada y una salida en correspondencia por lo propuesto en 15, con estructuras Error de salida (OE) y Autorregresivo con entrada exógena (ARX), para diferentes órdenes, de los cuales se obtuvieron sus equivalentes continuos.
En cada caso, los modelos estimados reflejaron el comportamiento del subproceso de postcombustión de forma adecuada de acuerdo al comportamiento real observado, lo que constituye una premisa importante para el diseño de estrategias de control de elevado desempeño, donde es necesaria una fase de simulación.
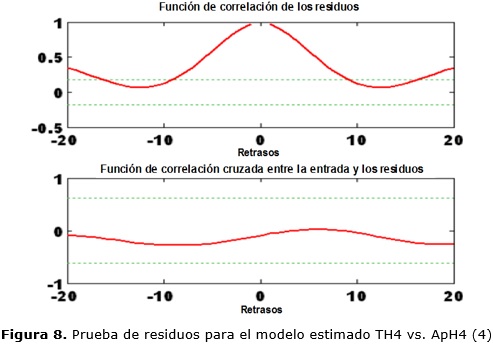
Con respecto a la validación de los modelos, se efectuaron análisis de residuos (errores de predicción) y correlación cruzada, tal como se propone en 16 y 3 respectivamente. Los resultados asociados a la variación de la apertura de la válvula respecto a la temperatura del hogar 4, se muestran en la figura 8; donde la función de correlación de los residuos se encuentra dentro de los niveles de confianza, y la función de correlación cruzada arrojó que no hay correlación entre los residuos y la entrada.
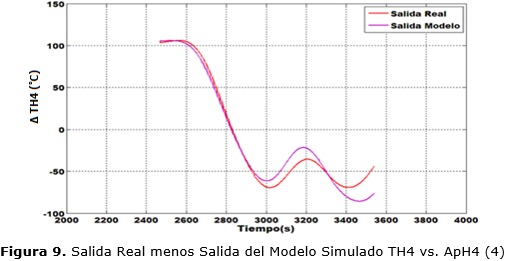
En la figura 9 se observa la comparación de la salida medida con la salida del modelo, estimada para un horizonte de predicción infinito. Para ello se tomó una parte de los datos originales que no fueron empleados para la estimación del modelo. El modelo obtenido evidencia mayor por ciento de ajuste en relación con el modelo propuesto en 6 y su comportamiento resulta representativo a la dinámica del sistema.
· Modelos obtenidos variando la apertura de la válvula del hogar 4:
OE 233 con un ajuste de 83,05 %.
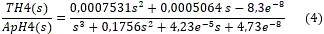
ARX 331 con un ajuste de 73,21 %.
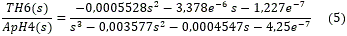
ARX 222 con un ajuste de 74,21 %.
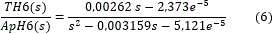
· Modelos obtenidos variando la apertura de la válvula del hogar 6:
ARX 333 con un ajuste de 63,43 %.
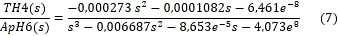
· Modelos obtenidos variando el flujo de mineral:
OE 233 con un ajuste de 84,34 %.

OE 233 con un ajuste de 80,12 %.
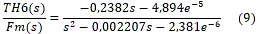
DISEÑO DE LA ESTRATEGIA DE CONTROL
Al analizar los sistemas multivariables una de las cuestiones fundamentales es determinar la mejor pareja variable controlada-variable manipulada. La principal característica que poseen estos sistemas es la interacción entre las variables, para ello se realiza un análisis utilizando el método de Matriz de Ganancia Relativa (MGR) basado en álgebra simple. 17
Primero se debe de obtener la matriz de las ganancias a estado estacionario (K) aplicando las ecuaciones (10) y (11), las cuales emplean los modelos (4, 5, 6, 7, 8, 9).
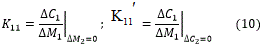
La relación entre K11 y K11' es llamada la ganancia relativa (λ11):
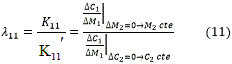
Cada una de estas ganancias se obtuvieron utilizando el comando zpk de la caja de herramientas de sistemas de control del MATLAB y se muestran en (12).
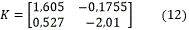
Aplicando la ecuación
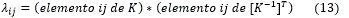
Donde la inversa de K (K-1) se calcula de la siguiente forma:
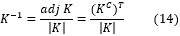
Se obtienen la matriz adjunta de K (adjK) y el determinante |K|, parámetros que son necesarios para poder calcular la matriz inversa.
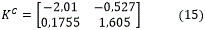
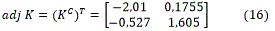
|K|=-3,13
Una vez obtenidos estos parámetros se procede a realizar el cálculo de la matriz inversa de K.
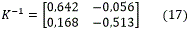
Debido a que cada uno de los elementos de la MGR se calculan partiendo de la ecuación 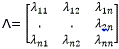 , es necesario hallar la transpuesta de la matriz inversa de K ([K-1]T).
, es necesario hallar la transpuesta de la matriz inversa de K ([K-1]T).
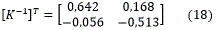
Luego de tener la transpuesta de la matriz inversa se procede a calcular la MGR (E) teniendo presente el lugar de cada uno de sus elementos.
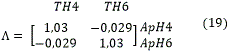
La pareja escogida es: el flujo de aire en el hogar 4 (ApH4) con la temperatura en el hogar 4 (TH4) y el flujo de aire en el hogar 6 (ApH6) con la temperatura en el hogar 6 (TH6), ya que Bristol recomienda que el emparejamiento se debe realizar de forma que las ganancias relativas correspondientes sean positivas y tan cercanas a uno como sea posible.
Como se puede apreciar λ12 y λ21 son distintas de cero, por tanto se puede decir que el sistema presenta interacción, para ello es necesario el uso de los desacopladores para disminuir dicha interacción.
Cálculo de los desacopladores
Para compensar la interacción del lazo 1 sobre el lazo 2 se introduce el desacoplador D21 y para la del lazo 2 sobre el lazo 1 se introduce el desacoplador D12.
Para calcular cada uno de estos, es necesario utilizar la ecuación I.N=|K|/ (Πi=1nKii), quedando de la siguiente manera:
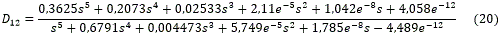
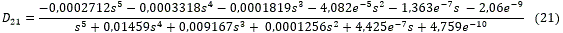
Estabilidad del sistema
Luego de haber obtenido la MGR empleando la regla de acoplamiento entre las variables y de comprobar que el sistema cumple con la regla de acoplamiento del Teorema de Niederlinski; se procede a obtener el índice de Niederlinski (I.N = 0,97 > 0), por lo cual se puede decir que el sistema no es inestable.
Parámetros de los controladores
Un método utilizado en la actualidad para el ajuste de los controladores es la herramienta PID Tuner del MATLAB, la cual fue utilizada para obtener cada uno de los parámetros de los controladores.
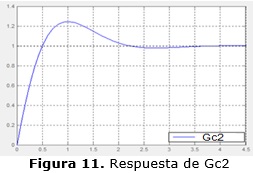
Después de realizar cada uno de los pasos y regulando el tiempo de respuesta hasta que el sistema sea estable, se obtienen los siguientes parámetros de los controladores (Gc1 y Gc2, controladores con estructura PID) con sus respectivas respuestas (figura 10 y figura 11), en las cuales se muestran cómo responden los sistemas hasta alcanzar el estado estable.
Para el primer controlador (Gc1):
Kp = 2575,597; Ti = 1685,4468
Para el segundo controlador (Gc2):
Kp =1049,4078; Ti = 2024,4964
En la figura 12 se muestra la estrategia de control multivariable para el subproceso de postcombustión.
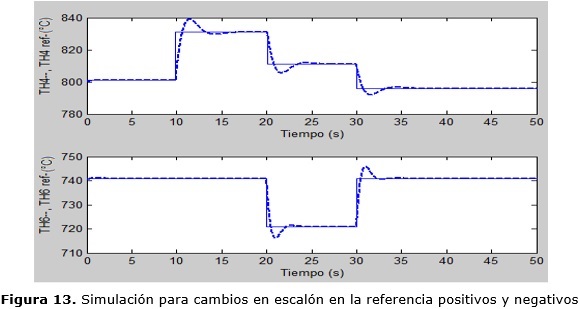
En la figura 13 se observan las respuestas de las temperaturas TH4 y TH6 cuando se producen cambios en escalón, positivos y negativos en sus respectivas referencias. Al transcurrir 10 segundos se observa que la temperatura TH4 aumenta al producirse un aumento en la referencia de 20 ºC. Pasados 10 segundos se producen dos disminuciones de 20 ºC en las referencias de TH4 y de TH6. Al cabo de 10 segundos se provocan dos cambios; un aumento en TH6 ref y una disminución en TH4 ref de 20 ºC.
Se aprecia en todos los casos un transitorio moderado, por ejemplo: ante el primer cambio en la referencia de TH4 el máximo sobrepaso fue de 10 ºC, el tiempo de pico de 1,45 segundos y el tiempo de establecimiento de 4,2 segundos; para el primer escalón en TH6 ref un máximo sobrepaso negativo de - 4 ºC, el tiempo de pico de 1 segundo y el tiempo de establecimiento de 2,1 segundo, mostrando la estabilidad del sistema.
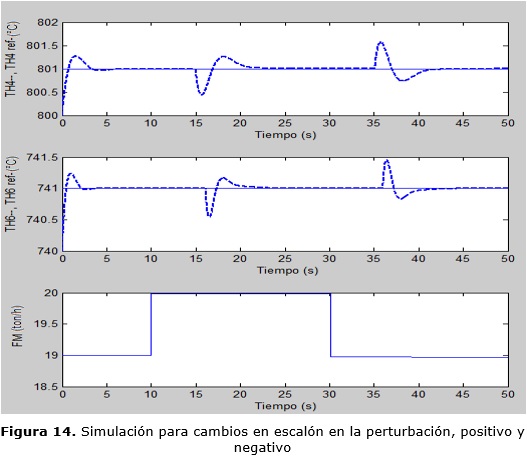
En la figura 14 se muestran las respuestas de la temperatura en los hogares 4 y 6 cuando se produce un cambio en escalón de 1 tn/h en el flujo de mineral (perturbación) al cabo de 10 segundos en ascenso y luego a los 30 segundos en descenso, las temperaturas se desvían y regresan en breve al valor deseado; lo que muestra las bondades del sistema de control diseñado.
CONCLUSIONES
Se obtuvieron modelos matemáticos lineales sobre la base de la identificación experimental aplicando como señal de excitación secuencias binarias de amplitud modulada, alcanzándose ajustes máximos del 84,34 % para la estructura Error de Salida (OE) y 74,21 % para la estructura ARX,.
En cuanto al algoritmo de control para la temperatura en los hogares 4 y 6 del horno, se diseñaron los controladores con la ayuda de la herramienta PID Tuner del MATLAB. Se comprobó mediante el método de Matriz de Ganancia Relativa la interacción entre las variables del subproceso de postcombustión. Se calcularon los desacopladores para propiciar la disminución de dicha interacción. Luego se procedió a la simulación del sistema aplicando cambios en la entrada y en la perturbación apreciándose en todo momento que el sistema sigue la referencia y mantiene su estabilidad. Los modelos obtenidos constituyen una plataforma de prueba muy valiosa para posteriores investigaciones que se pretenden acometer en el sistema objeto de estudio.
REFERENCIAS
1. CASTELLANOS, J; CASTO, R; GARCÍA, I. «Elaboración de minerales oxidados de níquel por el esquema carbonato amoniacal». Minería & Geología, 1986. 4 (2): 77-91.
2. MIRANDA, J; CHAVIANO, R; MIRANDA, J. R. «Nuevas Interpretaciones químico-mineralógicas de las menas lateríticas y serpentínicas, a través del proceso pirometalúrgico, en la tecnología carbonato-amoniacal». Revista Cubana de Química, 2002. 14 (2): 42-50.
3. RAMÍREZ, M. «Modelado del proceso de postcombustión en un horno de reducción de níquel». Revista de Metalurgia, 2002. 38 (2): 150-157.
4. CALDAS, O; JIMÉNEZ, S; MEJÍA, E; HERNÁNDEZ, J; AVILÉS, O. «Identificación paramétrica en lazo cerrado de sistema de accionamiento neumático para cilindro de doble efecto». Revista Facultad de Ingeniería UPTC. 2012. 21(33): 9-19.
5. RAMÍREZ, M. «Identificación experimental del subproceso de postcombustión en un horno de reducción de níquel». Minería & Geología, 2001.18 (2): 61-66.
6. MONTERO, D; RAMÍREZ, M. Identificación experimental del subproceso de postcombustión en un horno de reducción de níquel, ENERMOA, ISMM, Moa, Cuba. 2012. ISBN: 958-959-16-2067-5.
7. MANUAL DE OPERACIONES de la Planta Hornos de Reducción de la empresa «Comandante Ernesto Ché Guevara» de Moa. 2007.
8. TAVÍO, G. Optimización de la reducción de níquel en los hornos de reducción equipados con cámaras PRIOR. Santiago de Cuba: XVI Conferencia de Química. 1999.
9. NATH, N; CHAKRABORTIAND, N; SHEKHAR, R. «Reduction of Indian nickeliferrous ore in a fixed bed reactor with gas flowing vertically through the bed». Scandinavian Journal of Metallurgy, 1998. 27(1):14-22.
10. TORRES, G. Modelación matemática para predecir el comportamiento del extractable de níquel en los Hornos de Reducción. Tesis de Maestría. Universidad de Oriente. 1999. 80p.
11. ISERMANN, R. Identification of dynamic systems. An introduction with application. Springer Berlin Heidelberg. 2011. ISBN 978-3-540-78878-2.
12. ROFFEL, B; BETLEM, B. Process dynamics and control: modeling for control and prediction. John Wiley & Sons, New Jersey, 2006.
13. AÑEZ, G; SCARANO, M. «Modelado experimental del nivel de un tanque de agua en una planta piloto». Telematique, 2015. 14 (1):58-78.
14. LJUNG, L. System Identification Toolbox. User's Guide. New Jersey: Prentice-Hall. 2012.
15. ESTRADA, I; PEÑA, J; GUARNIZO, C. «Estimación de modelos lineales para el control predictivo de pequeñas centrales hidroeléctricas». Revista Soluciones de Postgrado EIA, 2012. (9): 63-78.
16. LJUNG, L; GUO, L. «The role of model validation for assessing the size of the unmodeled dynamics». IEEE Transactions on automatic control, 1997.42 (9): 1230-1239.
17. LIU, T. Industrial Process. Identification and Control Design. Step test and Relay experiment based methods. Springer Dordrecht Heidelberg London New York. 2012. ISBN 978-0-85729-976-5.
Recibido:10 de enero de 2015
Aprobado: 17 de mayo de 2015
Deynier Montero Góngora, Instituto Superior Minero Metalúrgico de Moa (ISMMM), Holguín, Cuba. E-mails:dmonterog@ismm.edu.cu, mramirez@uo.edu.cu , aghernandez@ismm.edu.cu, scampos@ecg.moa.minem.cu