Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Electrónica, Automática y Comunicaciones
versión On-line ISSN 1815-5928
EAC vol.39 no.1 La Habana ene.-abr. 2018
ARTÍCULO ORIGINAL
Constelaciones No-Uniformes en 1D para el estándar DTMB
Non-Uniform Constellations in 1D for DTMB standard
Ernesto Fontes Pupo, Reinier Díaz Hernández, Yoania Acosta Cintado
Instituto de Investigación y Desarrollo de Telecomunicaciones, La Habana, Cuba.
RESUMEN
El objetivo de este artículo es diseñar Constelaciones No-Uniformes en 1-Dimensión para el estándar DTMB y evaluar en cuanto mejora su desempeño con respecto a la utilización de la capacidad del canal. La utilización de dichas constelaciones ofrece una mayor eficiencia espectral, recepción a menores valores de Relación Señal a Ruido y acercar al estándar DTMB al límite teórico de Shannon. Dichas constelaciones, son diseñadas siguiendo el criterio de optimización de la capacidad del BICM. El sistema DTMB con las Constelaciones propuestas es validado mediante el análisis de las curvas BER, Capacidad y Eficiencia Espectral contra Relación Señal a Ruido, en todos los casos se compara contra el estándar original. Todas las pruebas son realizadas para las diferentes razones de código que permite el estándar, para 6 MHz de ancho de banda y siempre para un modelo de canal AWGN. En el artículo se presentan los fundamentos teóricos relacionados con la capacidad del canal y con las constelaciones Uniformes y No-Uniformes, así como se describe el algoritmo de diseño utilizado y se presentan las características de las constelaciones resultantes.
Palabras claves: 1D NUC, QAM, capacidad del BICM, capacidad del canal, límite de Shannon, DTMB.
ABSTRACT
The aim of this paper is to design 1-Dimensional Non-Uniform Constellation for DTMB standard and evaluate their performance improvements with regard to channel capacity. The use of such constellations offers a biggest spectral efficiency, reception at lower Signal to Noise Ratio and a Shannon limit gap reduction. Such constellations are designed based on the BICM optimization criterion. The DTMB system with the proposed constellations is validated by mean the analysis of BER, Capacity and Spectral Efficiency vs. Signal to Noise ratio. The results are always compared with the original standard. The simulations take into account the different available code rates of the standard, 6 MHz of bandwidth and AWGN channel model. The paper present the theoricals fundamentals of channel capacity, Uniform and Non-Uniform constellations and the description of the design algorithm. Moreover, the characteristics of the resulting constellations are shown.
Key words: 1D NUC, QAM, BICM capacity, channel capacity, Shannon limit, DTMB.
1.-INTRODUCCIÓN
En los últimos años diferentes tecnologías de codificación/decodificación de canal han sido implementadas en los estándares de Radiodifusión de Televisión Digital Terrestre (DTTB). Estas tecnologías están encaminadas a reducir la brecha con respecto al límite de Shannon de estos sistemas y todas están sujetas a un proceso continuo de optimización y cambio. Ejemplos de estas son: la codificación LDPC (Low Density Parity Check), Layer Division Multiplexing (LDM) [1], MIMO (Multiple-input-multiple-output), BICM (Bit-Interleaved Code Modulation) y NUC (Non-Uniform Constellation). Desde la primera y segunda generación de estándares de TDT, tal y como se definen en [2], hasta el estándar de nueva generación ATSC 3.0, [3], estas tecnologías han sido incorporadas progresivamente. Esto ha permitido una utilización más eficiente de la capacidad del canal, es decir, recepción a una menor Relación Señal a Ruido (SNR), mayor velocidad de transmisión y en sentido general, sistemas más robustos. [4]
Una de las nuevas tecnologías que posibilita utilizar de una manera más eficiente la capacidad del canal de transmisión, es la optimización de las comúnmente utilizadas Constelaciones Uniformes (UC). Estas optimizaciones están basadas en técnicas de conformación de señales (del inglés, constellation shaping techniques), las cuales se pueden dividir en dos grupos: conformación probabilística y conformación geométrica [4]. Las NUCs son una forma de conformación geométrica, estas pueden ser diseñadas en 1D o 2D (dos-dimensiones). En el 2012 estas fueron adoptadas por el estándar DVB-NGH (Next Generation Handheld), [5], y más recientemente por el estándar ATSC 3.0, [3].
El estándar DTMB (Digital Terrestrial/Television Multimedia Broadcasting) pertenece a la primera generación de estándares de TDT [2]. Debido a esto, de las tecnologías anteriormente mencionadas solo incluye en su cadena de codificación/decodificación de canal la codificación LDPC, tal como se puede ver en [6]. De aquí que su utilización de la capacidad del canal está lejos del límite de Shannon en comparación con los estándares de segunda y de nueva generación. El objetivo de este trabajo es evaluar para el estándar DTMB, cual es el impacto de la utilización de Constelaciones No-Uniformes en 1-Dimension, o sea cuanto mejora su desempeño respecto a los parámetros antes mencionados. Para esto, se diseñan 1D NUCs para 16 y 64-QAM y para las diferentes razones de código del estándar DTMB (0.4, 0.6, 0.8). Estas fueron diseñadas siguiendo los criterios de optimización de la capacidad del BICM descritos en [7] y [8].
Este artículo está compuesto por: Sección 1 y Sección 2 donde aparecen la introducción y los fundamentos teóricos respectivamente. En la Sección 3 se describe el diseño de las 1D NUCs y en la Sección 4 se muestra la validación de los resultados. Finalmente, en la Sección 5 se presentan las conclusiones del artículo.
2.- FUNDAMENTOS TEÓRICOS, CAPACIDAD DEL CANAL
Desde 1948 Claude E. Shannon en su trabajo “A mathematical theory of communication” definió el máximo throughput posible sobre cualquier canal de transmisión como capacidad del canal (CC) [9]. Para explicar esto, primero se verá el concepto de entropía H(sk) definido por Shannon en su teorema sobre la codificación de la fuente de datos, que establece que: H(sk) es el promedio mínimo de numero de bits por símbolos que son necesarios para codificar sk (entrada del canal de transmisión.) [9]. Para el receptor H(sk) es una medida para la incertidumbre de los símbolos transmitidos sk. Por medio de la observación del canal rk, esta incertidumbre puede ser convertida en información, aunque una parte es inevitablemente perdida debido a las características propias del canal de transmisión. Estas pérdidas están determinadas por la entropía condicional H(sk│rk). El throughput de la información es la diferencia de dichas entropías y es conocido como información mutua (MI) o transinformación entre sk y rk. [7]
I(sk, rk) = H(sk)−H(sk │rk) (1)
La MI I(sk,rk) es una medida de la información que la recepción de rk provee de sk. Evidentemente 0 ≤ I(sk,rk) ≤H(sk), el límite inferior ocurre cuando rk y sk son independientes y el superior solo ocurre para canales de transmisión ideales. [7]
2.1- LIMITE DE CAPACIDAD
En [9] se define la CC como la máxima MI I(sk,rk) entre la entrada del canal sk y la salida rk para todas las posibles distribuciones p(xl) de un alfabeto de símbolos arbitrarios X. [7]
Un sistema de comunicación real es solo posible, si el número de bits de información por cada símbolo transmitido, η=Rc·M (Rc: razón de código, M: número de bits por símbolo), no excede la capacidad del canal, es decir, η≤ CC. En otras palabras, el bitrate máximo posible para un canal de ancho de banda B en bits por segundo es CC ·B. [7]
Para canales AWGN la capacidad del canal puede ser calculada según la Ecuación 3, siendo el SNR la relación señal a ruido del sistema. CC es el límite superior del canal, el cual nuca va a ser alcanzado por sistemas de comunicación prácticos, dado que asume que un número infinito de símbolos es transmitido y que la modulación y la demodulación son ideales.
2.2- CAPACIDAD DEL BICM
En los sistemas de comunicación prácticos el número de símbolos no puede ser infinito. En esquemas de modulación QAM se define un número de símbolos L, siendo │ X │ = L (en este trabajo se asumen símbolos equiprobables), usualmente L = 2M. Teniendo esto en cuenta, se define la capacidad CS (capacidad del set de señales) la cual es una versión menos idealizada del límite de la capacidad.Agregando la restricción al sistema de que el de-mapeo se realiza solo una vez, se puede calcular la capacidad del BICM (del inglés, bit interleaver coded modulation) CB (Ecuación 4) como la MI entre los símbolos transmitidos sk y la salida del módulo de de-mapeo. En contraste con CS, el cual es determinado solo por el alfabeto de símbolos del sistema, X, la capacidad del BICM depende también de la función de mapeo (µ) de estos símbolos en la constelación. De aquí que la vía para maximizar CB es mediante la optimización del mapeo de los símbolos en la constelación. [7]
El análisis comparativo que se realiza en [7] sobre los tres límites de capacidad que se han presentado muestran que CC > CS≥ CB, esto se debe a los diferentes niveles de idealización que tienen estas tres definiciones. Además, se muestra que, a medida que el orden de las constelaciones aumenta, la diferencia de CB con respecto al límite de Shannon, CC, aumenta (Figura 1 (a), (b)). La vía para disminuir esta separación con respecto al límite de Shannon es mediante la utilización de las NUCs, optimizándose de esta manera la µ y en correspondencia el CB.

3.- 1D NUC / UC
3.1- CONSTELACIONES UNIFORMES
El mapeo de símbolos consiste en recibir cada Ts (período de símbolos) un vector ck de M bits y devolver un símbolo complejo sk∈Xque depende de la función de mapeo µ, es decir sk = µ(ck). La constelación QAM es totalmente definida por el alfabeto de símbolos │ X │ = L (L = 4, 16, 64,…) y la función de mapeo µ. Cada símbolo dentro de la constelación como anteriormente se mencionó, se asume que tiene igual probabilidad de ocurrencia P[sk]= L-1 [7]. La potencia promedio de símbolos Px =Esk[│s│2] de una constelación va a depender del sistema en particular con el que se esté trabajando. En DTMB para 16-QAM Px =40 y 42 para 64-QAM. La función de mapeo de los símbolos dentro de la constelación normalmente es del tipo Gray. Cualquier constelación en la cual los símbolos que se encuentran a la distancia mínima dmin difieren en más de un bit no cumplen con la definición de las distribuciones Gray, ver detalles en [7].
Las UC QAM se caracterizan por tener un espaciamiento uniforme entre los puntos de la constelación y una forma cuadrada de la constelación. Este tipo de constelación ha sido utilizado en diferentes estándares de comunicación debido a su simplicidad para codificar y decodificar. Sin embargo, hay una separación significativa entre la capacidad BICM CB de las UC QAM y el límite teórico de Shannon, (Figura 1) [10]. El estándar DTMB define las siguientes constelaciones: 64-QAM, 32-QAM, 16-QAM, 4-QAM y 4-QAM-NR [6]. En este trabajo solo se presentaran optimizaran para las constelaciones 64-QAM y 16-QAM.
3.2- CONSTELACIONES NO UNIFORMES EN 1DIMENSIÓN (1D-NUC)
El concepto de 1-dimensión se refiere al hecho de que una modulación QAM que se compone por 2-dimensiones (parte real (I, en fase) e imaginaria (Q, en cuadratura)) puede ser descompuesta en dos constelaciones PAM (modulación de amplitud de pulso) de 1-dimensión. Una para cada componente en fase I y en cuadratura Q, los cuales pueden ser demoduladas independientemente. Por tanto, dos demoduladores PAM son suficientes para demodular un 1D NUCs. En la práctica, estas constelaciones son descritas solamente por la parte real de cada punto y se determina su posición en el plano de dos dimensiones por simetría.
Las 1D NUCs son diseñadas obviando la condición de que en las UC la dmin tiene que ser idéntica entre todos los puntos contiguos [10]. Eliminar esta restricción define un nuevo concepto para las constelaciones QAM que es: los grados de libertad DOFs (Degrees of Freedom) de los puntos de la constelación. En estas constelaciones los DOFs están limitados en una sola dimensión [11]. Por ejemplo, una constelación 64 QAM tiene 8 DOFs en la parte real que es donde se realiza la optimización. Teniendo en cuenta la simetría con respecto al cero, las 1DNUCs de 64-QAM se diseñan solo considerando 4 grados de libertad. A medida que aumenta el orden de las NUCs aumenta la ganancia dado que aumentan los grados de libertad para la optimización.
3.3- DISEÑO DE LAS 1D-NUCs
Dado lo analizado anteriormente, el objetivo es maximizar la capacidad del BICM, CB, mediante la optimización del mapeo de los símbolos en la constelación en una dimensión (parte real). CB depende de las probabilidades de transición del canal p(rk│sk= xl) (ecuación 4) las cuales a su vez dependen del SNR(ver detalles matemáticos en [7]). Por tanto, diferentes NUCs resultarán para un canal AWGN para cada valor de SNR [4].
Según [4] mediante las curvas de BER (razón de bis erróneos) contra SNR que caracteriza cada razón de código LDPC, se puede determinar con facilidad el SNR que se tomará como criterio de diseño. Es decir, para cada razón de código se selecciona el SNR de la región de caída (el SNR donde los valores del BER disminuyen en varios órdenes) de la curva correspondiente [4]. De esta manera se logran mejores resultados con el algoritmo de optimización, independientemente de los diferentes SNR en los que se emplea cada NUC. Cuando una NUC se está utilizando por debajo del SNR para el que fue diseñada es imposible realizar una decodificación exitosa, debido a que el código corrector de errores no está seleccionado para estas condiciones. Si por el contrario el SNR es mayor, la decodificación es todavía posible, aunque la NUC no se optimizara para esos SNRs particulares. [4]
En la Figura 2 se muestran las regiones de caída de los diferentes modos del estándar DTMB obtenidos en este trabajo. En la Tabla 1 se muestran los valores de SNR para los cuales se optimizaran las constelaciones. Estos resultados se pueden validar contrastándolos con los valores obtenidos en [12], [13] y [14].
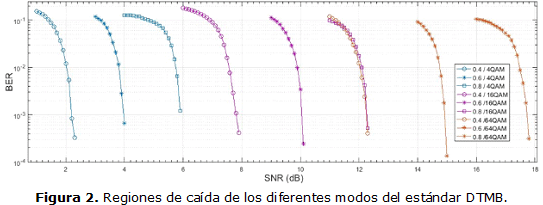

Una vez determinados los SNRs para los cuales se tienen que optimizar las NUCs se empleó el procedimiento de diseño presentado en [8].
3.3.1- 16-QAM
La modulación 16-QAM es el caso más sencillo de optimizar y con el que menos ganancias se logra. Este solo tiene 4 DOFs para las 1D NUCs y teniendo en cuenta la simetría solo se consideran 2 DOFs para la optimización. Considere una 16-QAM uniforme con mapeo de sus símbolos en {-3, -1, +1, +3} y utilizando Gray (se utilizó un mapeo Gray para todas las NUCs). Téngase en cuenta que se quiere diseñar una 1D NUCs, por esto solo se considera la dimensión real y luego cualquier optimización que se obtenga en esta dimensión por simetría se le aplica a la parte imaginaria. Evaluando esta constelación en CB para un SNR de 8 dB (caso 0.4/16-QAM, ver Tabla 1, los resultados obtenidos a continuación se aplican exactamente para los restantes SNRs) se obtiene una capacidad del BICM de 2.6782 bit/s/Hz. El objetivo es lograr para un mismo valor de SNR y una misma L=16, un mayor valor de capacidad y en consecuencia lograr una curva correspondiente de región de caída (Figura 2) con el mismo valor de BER para un SNR menor.
Para lograr esto se define el siguiente mapeo de símbolo: {-a, -1, +1, +a}, donde a representará el grado de libertad mediante el cual se optimizará. Para SNR = 8 dB podemos calcular y graficar la capacidad del BICM como una función de a y de esta manera determinar el valor de a (a≥ 1) para el cual CB es máximo, ver Figura 3. Se utilizó una resolución de 0.1 para los diferentes valores de a. Los detalles matemáticos de como evaluar CB tanto para las NUCs de 16 como de 64 QAM se pueden encontrar en [8]. Para realizar las optimizaciones se utilizó el asistente matemático MuPAD de Matlab.
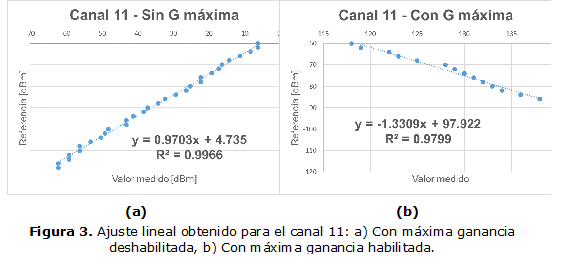
Los resultados muestran que para a = 3.7 el valor de CB alcanza el pico máximo de 2.6951 bit/s/Hz. Esto representa una ganancia de 0.0169 sobre la constelación uniforme. En el epígrafe 4 se realiza un análisis de estos resultados. La nueva constelación 1D NUC 16-QAM se muestra en la Figura 4.
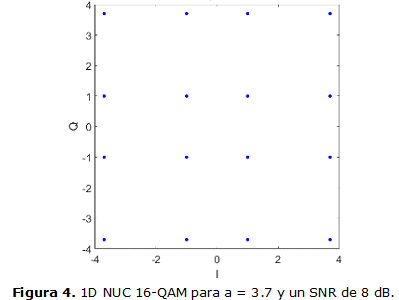
En la Figura 5 se muestra como queda la gráfica de CC contra SNR para esta nueva constelación no uniforme. Esta gráfica igualmente evidencia la ganancia con respecto a la UC.

3.3.2- 64-QAM
El mismo método utilizado para las 16-QAM se extiende para las 64-QAM y para constelaciones de mayor orden. Solo se tienen que definir más parámetros en dependencia de los DOFs sobre los cuales optimizar. Considere una 64-QAM uniforme con mapeo de sus símbolos en {-7, -5, -3, -1, 1, +3, +5, +7}. El valor de CB para un SNR de 12.4 dB (caso 0.4/64-QAM, ver Tabla 1, los resultados obtenidos a continuación se aplican exactamente para los restantes SNRs) es de 3.9022 bit/s/Hz. En este caso se define el siguiente mapeo de símbolos para la optimización: {-c, -b, -a, -1, 1, +a, +b, +c}. Con estos parámetros no es posible utilizar una gráfica como en el caso anterior para encontrar el CB máximo. Para realizar estas optimizaciones se utilizó método iterativos matemáticos tal como se realiza en [8].
Utilizando este método iterativo para el caso de 16-QAM se impone la condición de que a≥ 1 [8]. Con esto se evita que se evalúen combinaciones innecesarias. Para el caso de 64-QAM se impuso la condición de que a, b, c≥ 1 y luego se evalúan todas las posibles combinaciones de a, b, c con una resolución de 0.1. De esta manera las iteraciones convergen al CB máximo para un SNR dado.
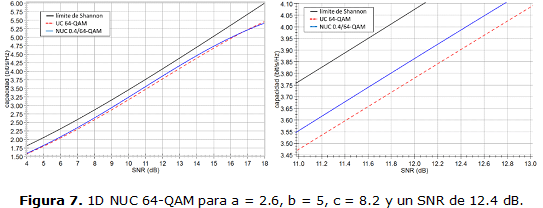
En este caso para un SNR de 12.4 dB el método arribó a CB máximo = 3.9861 bit/s/Hz para a = 2.6, b = 5, c = 8.2. Esto representa una ganancia de 0.0838 respecto a la constelación uniforme. La nueva constelación 1D NUC 64-QAM se muestra en la siguiente Figura 6.

En la Figura 7 se muestra como queda la gráfica de CC contra SNR para esta nueva constelación no uniforme. Esta gráfica igualmente evidencia la ganancia con respecto a la UC.
En la Figura 8 se muestra como queda la relación de CC contra SNR para todas las 1D NUCs diseñadas. Se puede ver como todas las curvas siguen las de las constelaciones uniformes, presentando las mayores ganancias en el rango para el que fueron diseñadas. Igualmente se puede apreciar como en todos los casos las de 64-QAM presentan mayor ganancia que las de 16-QAM, comprobándose que orden de la ganancia de las NUCs va a depender del orden de la constelación y los DOFs. En la Tabla 2 se hace un resumen de los valores de las NUCs diseñadas.


La Tabla 2 muestra como a medida que el SNR para el que las NUCs son diseñadas aumenta el resultado tiende a la UC y correspondientemente la ganancia tiende a cero.
4.- ANÁLISIS Y VALIDACIÓN DE LOS RESULTADOS.
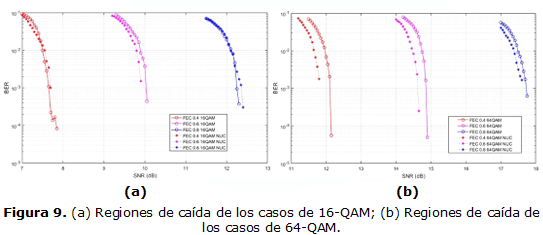
Luego de diseñadas las seis 1D NUCs se insertan en el sistema de transmisión y recepción del estándar DTMB y se evalúa en qué medida mejora este su desempeño. Primeramente se recalcularon las gráficas de las regiones de caída de BER contra SNR de los modos en los cuales se insertaron las 1D NUCs. En la Figura 9 se muestran los resultados de tanto las NUCs como las UC. El resultado esperado en todos los casos es que en los modos con NUCs siempre se obtengan resultados superiores. Los resultados en el modo con razón de código 0.8 y 16- QAM dieron mejor para el caso con UC, lo cual evidencia algún tipo de error en el sistema para este modo. En el epígrafe anterior se mostró que la NUC diseñada para este modo tenía ganancia de capacidad con respecto a la UC y comparando los resultados de las NUCs diseñadas con las obtenidas en [8], se puede validar que en todos los casos los diseños fueron correctos. Corresponde a un trabajo futuro corregir este problema en el modelo de Transmisión y Recepción de DTMB. En los demás casos los resultados se corresponden con los esperados y se demuestra la ganancia que supone utilizar las NUCs diseñadas en el sistema DTMB.
En la Figura 10 se muestra una comparación del sistema original y el propuesto en cuanto a Eficiencia Espectral y la Capacidad del sistema. Se evidencia que en el sistema con las NUCs propuestas se reduce la separación con respecto al Límite de Shannon y por tanto aumenta la Eficiencia Espectral. Esta gráfica igualmente muestra la manifestación del error antes mencionado para el caso con razón de código de 0.8 y modulación 16-QAM.

De las Figuras 9 y 10 se puede ver que la optimización de las NUCs representa una ganancia de SNR del sistema. Es decir, el SNR mínimo que se necesita para demodular correctamente cada uno de estos modos es menor. Por tanto la cobertura del servicio de TDT que se va a lograr para una misma potencia de transmisión será mayor. En la Figura 11 se representan cada una de estas ganancias de SNR con respecto al sistema con UC.
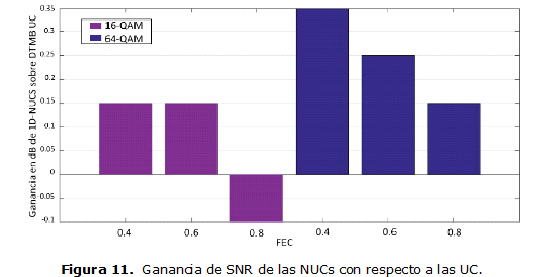
La gráfica muestra que la ganancia de SNR máxima que se logra con las NUCs es de 0.35 dB y la mínima de 0.15 dB. El caso en el que hay pérdidas es el mismo que se ha mencionado hasta ahora. La ganancia que se logró en todos los casos es pequeña. Esto se debe al orden de las constelaciones y los pocos grados de libertad que estas tienen para la optimización. No obstante si se comparan los resultados con los presentados en [15] y [4] con ATSC 3.0 (para SNRs de diseño similares), se puede comprobar que las ganancias obtenidas están en los mismos órdenes, lo cual valida los resultados obtenidos en este artículo. Para poder alcanzar ganancias mayores, para 16-QAM y 64-QAM es necesario diseñar las 2D NUCs que ofrecen mayores grados de libertad. Para los valores de SNR para los que se está diseñando, comparando de manera apreciativa con los resultados obtenidos en ATSC 3.0, para las 2D NUC 16-QAM la ganancia no sería mayor de 0.1 dB y para las 2D NUC 64-QAM la ganancia no sería mayor de 0.4 dB.
5.- CONCLUSIONES
En este artículo se presentaron Constelaciones no Uniformes en 1-Dimensión diseñadas para el estándar DTMB. Para el diseño se consideró un canal de transmisión AWGN en todos los casos. En total se propone el diseño de seis NUCs: tres para 16-QAM y tres para 64-QAM, teniendo en cuenta las tres razones de código LDPC que se utilizan en DTMB (0.4, 0.6, 0.8). La ganancia de SNR máxima que se logró fue de 0.35 dB y la mínima de 0.15. Con esta propuesta el desempeño del estándar mejora en cuanto a la Eficiencia Espectral, el SNR mínimo de recepción de los modos optimizados y finalmente se lograría un aumento de la cobertura del servicio de TDT si el estándar DTMB utilizara las NUCs propuestas.
REFERENCIAS
1. Acosta Cintado Y, Fontes Pupo E, Díaz Hernández R. Esquemas de multiservicios en DTMB, basados en técnicas de multiplexación LDM y TDM. Ingeniería Electrónica, Automática y Comunicaciones. 2017 Dec;38(3):85-99.
2. Dai L., Wang Z., Yang Z., Next-generation digital television terrestrial broadcasting systems: Key technologies and research trends. IEEE Communication Magasine. 2012; 50(6): 150–158.
3. Advanced Television Systems Committee. ATSC Standard: Physical Layer Protocol (Doc. A/322:2016). Washington, D.C.; 2016.
4. Loghin NS, Zöllner J, Mouhouche B, Ansorregui D, Kim J, Park SI. Non-uniform constellations for ATSC 3.0. IEEE Transactions on Broadcasting. 2016; 62(1): 197-203.
5. Digital Video Broadcasting. Digital Video Broadcasting (DVB): Next Generation broadcasting system to Handheld, physical layer specification (DVB-NGH), DVB Document A160.; 2012.
6. Standarization Administration of the People’s Republic of China. GB 20600-2006, Framing Structure, Channel Coding and Modulation For Digital Television Terrestrial Broadcasting System (DTMB). China; 2006.
7. Muhammad NS. Coding and modulation for spectral efficient transmission. PhD Thesis. Institute Nachrichtenübertragung, Stuttgart University, Stuttgart, Germany; 2010. Disponible en: http://elib.uni-stuttgart.de/bitstream/11682/2693/1/Dissertation_Nabil_Muhammad.pdf
8. Stott J. CM and BICM limits for rectangular constellations. BBC Research and Development WHP 257. 2012.
9. Shannon CE. A mathematical theory of communication. ACM SIGMOBILE Mobile Computing and Communications Review. 2001 Jan 1;5(1):3-55.
10. Michael L, Gómez-Barquero D. Modulation and Coding for ATSC 3.0. 2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Ghent; Belgium. 2015. p. 1-5.
11. Barrueco J, Regueiro C, Montalban J, Velez M, Angueira P, Kim HM, Park SI, Kwon S. Low complexity and high order two-dimensional non-uniform constellations for high capacity broadcasting systems. 2016 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Cagliari; Italy. 2016 pp. 1-5.
12. Standarization Administration of the People’s Republic of China. GB 20600-2006, General Specification for Digital Terrestrial Television Receiver. China; 2007.
13. Martínez Alonso A, Martínez Alonso R, Guillén Nieto G. Parámetros de calidad de recepción del estándar DTMB en 6MHz. 2014 IEEE Biennial Congress of Argentina (ARGENCON). Buenos Aires; Argentina. 2014. p. 381-386.
14. Martínez Alonso A, Martínez Alonso R, Guillén Nieto GA. Evaluación de parámetros de calidad seleccionados de Cajas Decodificadoras para el estándar DTMB. Ingeniería Electrónica, Automática y Comunicaciones. 2015 Aug;36(2):62-82.
15. Michael L, Gómez-Barquero D. Bit-interleaved coded modulation (BICM) for ATSC 3.0. IEEE Transactions on Broadcasting. 2016 Mar;62(1):181-188.
Recibido: 5/3/2017
Aceptado: 22/8/2017
Ernesto Fontes Pupo, Ing. en Telecomunicaciones y Electrónica, graduado en 2014 en la Universidad Tecnológica de La Habana (CUJAE). Desde septiembre 2014 se desempeña como investigador en el Instituto de Investigación y Desarrollo de Telecomunicaciones, LACETEL, radicado en La Habana, Cuba. Actualmente cursa la X edición de la Maestría en Sistemas Digitales. Las principales temáticas de investigación que desarrolla están relacionadas con las comunicaciones digitales y el procesamiento digital de señales en sistemas de radiodifusión. Correo electrónico: fontes@lacetel.cu













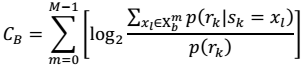 (4)
(4)
