Artículo original

Metodología y algoritmo de validación para identificar modelos de una unidad manejadora de aire.

Methodology and validation algorithm for the identification of models in an air handling unit.

0000-0002-8600-850XCarlos Alberto García Vázquez^{1  *  a}, 0000-0002-7969-4070Ana Isabel González Santos^{1  b}, 0000-0001-6382-7329Víctor Pérez Garrido^{2  c}

¹Universidad Tecnológica de La Habana José Antonio Echeverría (CUJAE), La Habana, Cuba

²Centro de Ingeniería Genética y Biotecnología (CIGB), La Habana

RESUMEN

Diferentes modelos matemáticos que describen el comportamiento de la temperatura y la humedad relativa en una unidad manejadora de aire (UMA) son obtenidos y validados a partir de datos experimentales reales. La identificación de sistemas es la metodología empleada, asumiendo la linealidad del sistema en el rango de operación de las variables de interés. El sistema se descompone en cuatro subsistemas, acorde a la dependencia de las variables temperatura y humedad relativa con las señales de control que reciben los actuadores que se usan para regular dichas variables, que son la válvula de tres vías y la válvula eléctrica. Para la estimación de parámetros se seleccionan diferentes estructuras lineales, concluyéndose la conveniencia de la estructura Box-Jenkins (BJ) para obtener modelos que relacionen las variables del sistema. La metodología utilizada es parcialmente programada, fundamentalmente las etapas de estimación de parámetros y de validación de modelos, lo que permite seleccionar con facilidad a los mejores modelos de entre un grupo de modelos candidatos para representar al sistema.

Palabras-clave: unidad manejadora de aire; identificación de sistemas; modelos lineales; estructura BJ; validación

ABSTRACT

In this work several mathematical models that describe the behavior of temperature and relative humidity in an air handling unit (AHU) are obtained and validated from real experimental data. System identification methodology is used assuming the linearity of the system within the range of operation of the key variables. System is decomposed in four subsystems according to the dependence of temperature and relative humidity variables with the control signals received by the three-way valve and the electric valve, actuators used to control the mentioned variables. Several linear structures were selected for parameter estimation, then the suitability of Box-Jenkins (BJ) structure to obtain models that relate the system variables was concluded. The methodology used is partially programmed, mainly parameters estimation and model validation steps, allowing the best models to be easily selected from a group of candidate models to represent the system.

Key words: air handling unit; system identification; linear models; BJ structure; validation

Introducción

Los sistemas de calentamiento, ventilación y acondicionamiento de aire (HVAC por sus siglas en inglés) han sido objeto de numerosos trabajos de investigación durante los últimos años. Una de las principales razones es que estos sistemas representan entre un 40 y un 50%, o más, del consumo total de energía de los edificios donde se encuentran instalados ^[1-^6], por lo que su operación eficiente resulta muy importante. También ha sido de interés el mejoramiento del confort térmico en los edificios y el diagnóstico y detección de fallos en el sistema de climatización. Una herramienta sumamente valiosa para los fines antes expuestos resulta el desarrollo de modelos matemáticos del sistema bajo estudio.

Al desarrollo exclusivo de modelos matemáticos se han dedicado trabajos como ^[7], donde se identifican modelos Box-Jenkins (BJ), autorregresivos con entradas externas (ARX), autorregresivos de media móvil con entradas externas (ARMAX) y error de salida (OE) para predecir valores futuros de temperatura y humedad en habitaciones, cuyo uso potencial sería mejorar el funcionamiento del sistema de control de clima. Para el futuro diseño de controladores con mejores prestaciones que los existentes, también en ^[8] se identifican modelos, en este caso, de función de transferencia en el dominio de Laplace. Este tipo de modelos también se hallan en [9] para trabajos de investigación relacionados con el diseño de sistemas de control, pero partiendo de ecuaciones diferenciales resultantes de aplicar las ecuaciones de balance para el proceso de clima en el edificio y la unidad manejadora de aire (UMA). En ^[10] se combina un modelo de Hammerstein con un modelo discreto en ecuaciones en diferencias, cuyos parámetros se obtienen mediante identificación de sistemas. El interés por reducir el costo computacional de estrategias como el control predictivo basado en modelo (MPC), conduce al uso en ^[11] de un modelo en el espacio de estados, obtenido mediante la aplicación de leyes físicas. En ^[5] se obtienen modelos de caja negra del sistema HVAC para diseñar estrategias de control avanzadas que reduzcan el consumo de energía. Para representar la dinámica de la UMA, se utilizan un modelo no lineal (red neuronal artificial), modelos lineales (ARX, función de trasferencia en el dominio de Laplace y modelo en el espacio de estados) y un modelo de caja gris. En las investigaciones ^[12-^14] el interés fundamental está en la simulación, que en el caso de ^[12] permite analizar la eficiencia del sistema HVAC y observar sus efectos en cuartos limpios, mientras que en ^[14] se busca predecir con exactitud el comportamiento de los componentes del sistema para permitir una mejor operación de este en función de disminuir el consumo energético. Mientras ^[12,^13] hacen uso de modelos de caja blanca, en ^[14] se usan máquinas de soporte vectorial y redes neuronales artificiales.

Respecto a las investigaciones dedicadas propiamente al control de sistemas HVAC, es común que dentro de sus objetivos se encuentren un buen seguimiento de referencias, respuestas rápidas, sobreimpulsos y tiempos de establecimiento pequeños y un menor consumo de energía, como se evidencia en ^[3, ¹⁵-^18]. El logro del confort térmico con un menor consumo de energía se busca en ^[19-^21]. Mientras que ^[2, ²²-^24] se concentran en la reducción del consumo de energía. En ^[25] el objetivo es mejorar la respuesta temporal del sistema controlado en cuanto a velocidad y estabilidad, en ^[26] se busca el rechazo a perturbaciones, seguimiento de referencias y diseño de observadores de estado, ^[4] se enfoca en el seguimiento de referencias y rechazo a perturbaciones armónicas, ^[27] en el desarrollo de un controlador no lineal que funcione correctamente en todo el rango de operación de la UMA, ^[28] en la mejora del confort térmico, ^[1] en un mejor seguimiento de trayectorias y ^[29] aborda tanto la simulación del consumo de energía como el diseño de un controlador predictivo y el diagnóstico y detección de fallos.

De las investigaciones anteriores se modela la UMA en ^[1, ³-⁵, ⁸-¹⁰, ¹³-¹⁸, ²⁰-^29] y predomina el uso de modelos basados en leyes físicas que conducen a una descripción del sistema mediante ecuaciones diferenciales que suelen llevarse al espacio de estados y que, en el caso de modelos no lineales, es común linealizarlos alrededor de uno o varios puntos de operación. Se observa que en todos los trabajos donde se utilizan modelos basados en leyes físicas no hay presencia de bancos de resistencias cuando se considera el calentamiento del aire y solo se mencionan en ^[8], donde se obtiene un modelo de caja negra.

En la industria farmacéutica, los sistemas HVAC deben garantizar el control de las partículas en suspensión, polvo y microorganismos (mediante el filtrado del aire), mantener presurizadas las áreas que deben permanecer más limpias que aquellas que les rodean, mantener determinada humedad relativa y determinada temperatura ^[30]. En las salas limpias las condiciones son auditables, por lo que deben garantizarse permanentemente, lo que hace que sea significativo el consumo de los sistemas HVAC en este tipo de industria, como se muestra en ^[6], concentrándose el mayor consumo en el enfriamiento y calentamiento ^[31]. De ahí que las estrategias de control que se diseñen para estos sistemas en este tipo de industria presenten el desafío de asegurar simultáneamente confort térmico y calidad del aire con el menor consumo de energía posible.

En el presente trabajo de investigación se estudió una UMA que climatiza varias salas limpias en un centro biotecnológico y en ella el control de la temperatura y humedad relativa del aire, lo cual involucra enfriamiento y calentamiento (mediante un banco de resistencias) del aire. El levantamiento instrumental aportó que los controladores PID fueron ajustados a prueba y error para unas condiciones diferentes a las actuales, ya que el deterioro de las enfriadoras de agua (chillers) provoca que la temperatura del agua fría supere el valor establecido por diseño, lo que lleva a la pérdida de efectividad del ajuste inicialmente propuesto, al no garantizar que todo el tiempo las variables se mantengan en los rangos establecidos, lo cual pudiera afectar la calidad del proceso desarrollado en las salas limpias. El centro produce uno de los candidatos vacunales cubanos contra la Covid-19 y puede ser inadmisible un deterioro del sistema de control de clima en las salas. Sobre la base del estudio realizado, se propone como solución la resintonía de los PID a partir de un modelo de la planta obtenido mediante identificación de sistemas, ya que, al no contarse con la licencia del software del PLC, no se puede modificar su programación para implementar otra estrategia de control. Por otra parte, con la adición de nuevas plantas de producción al centro, es necesario el diseño y ajuste de los controladores de las nuevas UMAs que las climatizarán, el cual, en la práctica, sigue haciéndose a prueba y error. Luego, el problema que se aborda va más allá de la UMA estudiada, pues las limitaciones actuales de su sistema de control probablemente se presenten en otras UMAs con tiempo de explotación y potencialmente también en las nuevas UMAs.

Por lo anterior, el objetivo del presente trabajo no es solo encontrar modelos de la UMA estudiada para la posterior resintonía de los PID, sino también mostrar que su identificación puede ser una herramienta segura, de bajo costo en tiempo y recursos y por lo tanto factible para que los proyectos de automatización de estos sistemas cumplan con todos los requerimientos antes mencionados respecto al tipo de industria donde se encuentran. Las contribuciones científicas de este trabajo son fundamentalmente de índole metodológica, ya que, aunque no hay un aporte a la metodología de la identificación de sistemas, sí se presenta una forma de llevarla a la práctica adecuada al proceso tratado. A partir de la experimentación y la simulación se sugieren las opciones de pretratamiento que ofrecen mejores resultados para este proceso. Los procedimientos seguidos se organizan e ilustran en forma de algoritmo, para su aplicación casi automática, explicándolos detalladamente. Ello pretende facilitar su sistematización y extender su aplicación práctica, carencia actual de muchos proyectos de ingeniería, como es el caso del realizado en el sistema estudiado y otros similares. Los resultados de la programación de una parte importante de estos procedimientos se muestran, permitiendo sugerir a determinada estructura, de la cual se obtienen familias de modelos, como una buena opción para representar la dinámica de los subprocesos de interés. Así se evidencia la posibilidad de obtener para ellos modelos fiables y sencillos, de forma segura, en un tiempo relativamente breve y con poco esfuerzo. Se incentiva la aplicación de esta metodología como paso previo e imprescindible al diseño de cualquier sistema de control, sea convencional o no, con el aval de los resultados de simulación del sistema controlado que se muestran también en el trabajo.

2.- Obtención y validación de modelos

La Fig. 1 muestra la metodología empleada para la obtención de modelos de caja negra, la cual se basa en las metodologías propuestas en ^[32-^34], y el algoritmo que se utilizó en la etapa de validación de dicha metodología.

Fig. 1 Metodología utilizada para la identificación de sistemas y algoritmo utilizado en la validación de modelos. 

2.1.- Estudio preliminar del proceso y selección de las variables de interés

Las UMAs son el componente fundamental de los sistemas HVAC ^[3]. Estas unidades permiten controlar variables como la temperatura, la humedad relativa y la velocidad del aire, y pueden ser de volumen de aire constante o variable. En el primer caso, la velocidad del ventilador es constante y controlan la temperatura y humedad relativa del edificio variando la temperatura y humedad relativa del aire suministrado; en el segundo caso, el flujo de aire es controlado ^[35]. Las UMAs pueden presentar diferentes configuraciones. Una de ellas es la mostrada en la Fig. 2, que se corresponde con la UMA estudiada, que climatiza varias salas limpias en el Centro de Ingeniería Genética y Biotecnología (CIGB) de La Habana. De izquierda a derecha en la imagen, la UMA consta de una sección de mezcla (en la cual el aire que retorna de los locales climatizados se mezcla con una porción de aire exterior), seguida por una sección de filtrado (prefiltro de mediana eficiencia seguido de filtro de alta eficiencia), una sección de enfriamiento (serpentín por donde circula agua enfriada a 7℃, cuyo flujo regula una válvula de tres vías), una sección de calentamiento (banco de resistencias eléctricas, regulado por un controlador de potencia trifásico con disparo por ráfagas y dos fases, al cual se le suele llamar válvula eléctrica, término que se utilizará en lo adelante) y una sección de impulsión (con un ventilador radial sin caracol tipo “plug fan”). El hecho de que las variables controladas están acopladas, que la carga es variable y que los elementos de las UMAs presentan una no-linealidad inherente, así como características variantes en el tiempo, constituyen dificultades a enfrentar para su modelado y control ^[35].

Fig. 2 Representación de la UMA P401 de la planta de producción del CIGB. 

La Fig. 3 muestra un diagrama del sistema de control actual para las variables temperatura y humedad relativa del aire en la UMA de la Fig. 2 ^[36]. Puede observarse un control en cascada en el cual los controladores PID se encuentran en el lazo interno, manipulando los flujos de corriente y agua fría que circulan por el banco de resistencias y el serpentín, respectivamente, mediante la válvula eléctrica y la válvula de tres vías. Estas variables físicas a su vez actúan sobre el proceso de clima dentro de la UMA. El proceso tiene como variables de salida la temperatura (TSu), medida en grados Celsius (ºC), y la humedad relativa (HuSu), en porcentaje (%), del aire suministrado por la UMA, las cuales constituyen la realimentación de los controladores PID. Este trabajo se centra en el lazo de control más interno. Por ello, el modelo que se obtiene para la resintonía de los PID debe tener a las anteriores variables también como salidas, siendo las señales aplicadas a las válvulas eléctrica (U_VE) y de tres vías (U_V3V), en el rango de 0-10V, las variables de entrada (los valores adquiridos para la identificación fueron los porcentajes que representan las tensiones de estas señales con respecto al máximo valor que pueden tomar). Debe aclararse que, en el diagrama, el bloque “resistencia” comprende a la válvula eléctrica y al banco de resistencias, mientras el bloque “agua fría” comprende a la válvula de tres vías y al serpentín.

Como recurso para la realización de experimentos se contó con un sistema SCADA que permite adquirir variables con intervalos de muestreo fijos a partir de un minuto o cada vez que ocurre un cambio en la variable. En el caso de los intervalos fijos, estos son de uno o varios minutos hasta varias horas. El sistema no permite otra frecuencia de muestreo aparte de las que ofrece para seleccionar, por lo que intervalos de muestreo fijos de 0.5 o de 1.5 minutos no se pueden utilizar.

Fig. 3 Sistema de control de temperatura y humedad relativa del aire actualmente implementado. 

2.2.- Diseño de experimentos, generación de señales, medición y recolección de datos

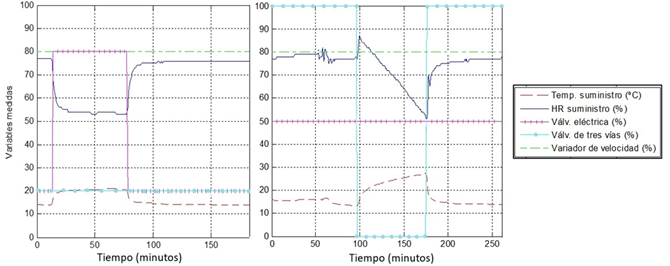
Como experimento inicial, se aplicaron entradas de tipo escalón a la válvula de tres vías y a la válvula eléctrica. Este experimento se realizó en lazo abierto, fijando las señales de control a valores constantes y variando manualmente una a la vez, como se muestra en la Fig. 4. El objetivo del experimento es obtener modelos de primer orden con retardo que relacionen cada salida con cada entrada, cuyos parámetros sirvan de base para el diseño del siguiente experimento.

Fig. 4 Experimentos aplicados con entradas de tipo escalón. 

Como se observa en la Fig. 4, se aplicaron pulsos de más de una hora de duración, los cuales se constituyen de un paso escalón en un sentido, llevando las variables de unos valores a otros, y luego un segundo paso en sentido contrario, retornándolas a los valores iniciales. Si se observa, luego del segundo paso escalón no se estabilizan exactamente en sus valores iniciales. Esto pudo deberse a la incidencia de perturbaciones, sobre todo, variaciones en la temperatura del agua fría, las cuales son comunes. En el caso del experimento en el que se varía la señal aplicada a la válvula eléctrica, se estimó para cada paso un modelo de primer orden con retardo. Los modelos observados en la Tabla 1 son el resultado de promediar ganancias, constantes de tiempo y retardos de los dos modelos estimados. En el caso de la variación de la señal aplicada a la válvula de tres vías, un mal funcionamiento de la válvula, que finalmente tuvo que ser cerrada manualmente, más la posible incidencia de perturbaciones, provocaron un comportamiento no esperado en las variables al aplicarles el primer paso escalón. De la experiencia que se tiene sobre el proceso, así como de la observación de la respuesta del sistema ante el segundo paso escalón aplicado a esta misma entrada, se concluyó que los datos producto del primer paso escalón debían ser desechados. Por lo tanto, sólo a partir de los datos del segundo paso se estimaron los modelos correspondientes a esta entrada que se muestran en la Tabla 1.

Debe mencionarse que, dado que se conoce la existencia no-linealidades en el proceso, una variante para tener una idea de la magnitud de las mismas alrededor del punto de operación de las variables, así como mejorar la aproximación de los modelos lineales, es dar los pasos escalones en las entradas a ambos lados del punto de operación. No obstante, para este proceso en específico, esto no siempre resulta práctico. En primer lugar, las variables analizadas en el aire de suministro no tienen un punto de operación, sino que transitan a lo largo de un rango de valores con el fin de mantener a las variables en el retorno dentro de su rango de operación, que sí es limitado. Por lo tanto, las señales de control normalmente recorren todos los valores que pueden tomar. Atendiendo a esto, se pudiera considerar tomar el 50% del valor de las señales de control para dar los pasos alrededor de dicho valor. No obstante, hay que considerar que la resolución de los instrumentos de medición es pobre y el proceso está sometido a perturbaciones; luego, la magnitud de los pasos debe ser tal que provoque una variación en las variables medidas lo suficientemente grande como para ser apreciada y claramente diferenciada del efecto de las perturbaciones. A la vez, no pueden ser tan grandes los pasos que saquen a las variables en el retorno de su rango de operación. Hay que tener en cuenta, además, que la temperatura del agua fría limita el efecto que pueda tener la apertura de la válvula de tres vías en las variables.

Sobre la base de lo anterior, el procedimiento utilizado para obtener datos útiles para la identificación de manera segura (sacando lo menos posible de su rango de operación a las variables en el retorno) fue fijar las señales de control de forma tal que las variables en el retorno tomaran valores cercanos a uno de sus límites de operación y que al dar los pasos en las entradas se movieran hacia el otro límite. Con esto se logró respetar los límites de operación establecidos para las variables en el retorno, así como dar pasos de una mayor amplitud para observar claramente la variación en el suministro y evitar, en la medida de lo posible, saturaciones debido a la temperatura del agua fría. Nótese que en las gráficas de la Fig. 4 los valores iniciales de las señales de control difieren, ya que los experimentos se realizaron en días y horarios distintos.

Tabla 1 Modelos de primer orden con retardo obtenidos como resultado de los experimentos con paso escalón 

	Temperaturasuministro(TSu)	Humedadrelativasuministro(HuSu)
Señala la válvula de tres vías(U_V3V)	$\frac{-0.134e^{-0.18s}}{3.5s+1}$	$\frac{0.25e^{-0.5s}}{4.43s+1}$
Señala la válvula eléctrica (U_VE)	$\frac{0.104e^{-0.1s}}{3.8s+1}$	$\frac{-0.396e^{-0.26s}}{3.4s+1}$

Para un segundo experimento, también realizado en lazo abierto, variando manualmente una entrada a la vez mientras las otras permanecen constantes, se escogió como estímulo una secuencia binaria pseudoaleatoria (PRBS). Esta selección responde a que se buscan, preferiblemente, modelos lineales y que la señal de estímulo debe ser persistentemente excitante ^[34]. Para el diseño de la PRBS, como norma general, el período de muestreo (T _s ) debe seleccionarse tal que 0,25τ ≤ T _s ≤ 0,5τ^[33], donde τ es la constante de tiempo del sistema. Dadas las constantes de tiempo previamente estimadas y las posibilidades que da el sistema SCADA para el muestreo de datos, tomar T _s = 1 min cumple con el anterior criterio para todos los subprocesos, salvo el de humedad relativa en función de la apertura de la válvula de tres vías. No obstante, en ^[34] se plantea que el período de muestreo puede tomarse menor, por lo que el criterio anterior no es tan rígido en cuanto al período mínimo. Por lo tanto, el período seleccionado sería válido para los dos experimentos con PRBS.

Para escoger el tiempo de pulso (T _p ) existe el criterio general de que 0,33τ ≤ T _p ≤ 3τ. También se recomienda que T _s se escoja de forma tal que T _p sea un múltiplo exacto de T _s ^[33]. Para cumplir con ambos criterios se escogió T _p =3T _s =3 min, lo cual pretende mejorar la estimación de la ganancia, al costo de disminuir la excitación de las altas frecuencias ^[34]. La longitud de la secuencia se calcula como, al menos, 5τ+L^[33], donde L es el retardo de tiempo del sistema. Este cálculo se corresponde aproximadamente con el tiempo de establecimiento del sistema, que resultó ser 17.26 min para la constante de tiempo más pequeña y 22.65 min para la mayor. El número de términos de la secuencia se calcula partiendo de dividir la longitud de esta entre el tiempo de muestreo. Luego se toma el menor resultado de la operación 2 ⁿ - 1 que sea mayor o igual que el cálculo anterior (n=1,2,3, ... es el número de etapas del registro de desplazamiento que genera la secuencia), que para todas las constantes de tiempo fue 31 (resultado de 2⁵ - 1), por lo que la secuencia tuvo 31 bits. Para tener más datos se aplicó dos veces consecutivas la secuencia generada, que fue utilizada para ambos experimentos, dada la similitud entre constantes de tiempo y los pequeños valores de los retardos.

Otro aspecto importante tenido en cuenta fue la amplitud de los pulsos. Para ello se debió mantener un compromiso entre dar pulsos en las entradas lo suficientemente grandes, como para observar claramente los efectos en las salidas, y que, a la vez, las desviaciones de las variables fuera del rango permitido en las salas limpias fueran muy pequeñas o no tuvieran lugar. En esto desempeñó un papel importante la experiencia ganada en los experimentos con paso escalón, así como el estudio del sistema. El conocimiento de que son mayores los retardos y constantes de tiempo de las respuestas de la temperatura y la humedad relativa en el aire de retorno de las salas, en comparación con los de estas variables en el suministro, es importante, pues la combinación de la amplitud seleccionada para los pulsos con el tiempo de duración de cada uno, puede contribuir a que las variables en las salas no se salgan de los límites, y si lo hacen, no mucho ni por mucho tiempo. Teniendo en cuenta lo anterior, se buscó además un par de valores máximo y mínimo para los pulsos tal que se cubriera el rango más usual de variación de las señales de control, al tiempo que la relación entre las variables se comportara aproximadamente lineal. Para realizar el experimento con la seguridad requerida, en la selección de la amplitud de los pulsos y sus valores máximos y mínimos, es importante, previo a la aplicación del experimento, observar los valores que en ese momento tienen las señales de control y la temperatura y humedad relativa, tanto en el suministro como en el retorno, y si es posible, el valor de la temperatura del agua fría, que, en este caso, se muestra en otro sistema SCADA.

Dado que no se dispuso de la licencia del software del controlador, no fue posible programar en este la generación de la PRBS diseñada. Por lo tanto, mediante el panel de operador se cambió el modo de operación de automático a manual, abriendo todos los lazos de control y, a través de los botones del módulo de salida del controlador, se aplicaron los estímulos con el apoyo de un reloj. A cada una de las entradas seleccionadas para la realización del experimento se le aplicó la secuencia diseñada manteniendo las demás constantes. Los valores de las variables de entrada y de salida fueron adquiridos mediante la aplicación Trend Viewer del Desigo Insight (sistema SCADA).

Debe mencionarse que no todos los datos fueron utilizados en la identificación. En el caso del experimento con la válvula de agua fría, un mal funcionamiento de esta obligó a desechar las primeras muestras. Además, en ambos experimentos se esperó a que las variables de salida se estabilizaran en uno de los dos extremos entre los cuales estuvieron variando. En la Fig. 5 se muestran los datos seleccionados para usarse en la identificación.

Fig. 5 Datos (selectos) recolectados de los experimentos. 

2.4.- Examen y análisis de los datos. Preprocesamiento

Una vez adquiridos y graficados los datos, lo primero que se comprobó fue que los estímulos en las entradas hubiesen sido aplicados tal cual se diseñaron, dada la forma en que se realizó el experimento. Siendo así, se comprobaron los niveles de excitación en las entradas con respecto a cada salida, que, para los datos de estimación (70% inicial de las muestras), fueron persistentemente excitantes y de órdenes 27, 41, 27 y 42, lo que significa que se deben estimar modelos de órdenes inferiores para las relaciones HuSu Vs U_V3V, HuSu Vs U_VE, TSu Vs U_V3V y TSu Vs U_VE respectivamente. Para este análisis, así como para los que a continuación se mencionan, se hizo uso del software MatLab® (versión 2013b).

A continuación, se inspeccionaron de forma visual las gráficas de la Fig. 5 en busca de valores anómalos (outliers), los cuales pueden originarse debido a inducción electromagnética, mal funcionamiento de los equipos de medición o errores en la transmisión de datos ^[34, ^37]. Esta es una forma empírica muy común, aunque subjetiva e inexacta, de detectar outliers basada en la experiencia ^[37], dado que las mediciones que se alejan considerablemente del rango esperado del proceso pueden considerarse potencialmente como datos anómalos ^[33].

Por otra parte, pudo apreciarse que durante el experimento en el cual se aplicó la señal de estímulo a la válvula de tres vías, la temperatura de retorno (TEx) se mantuvo todo el tiempo dentro de sus límites de operación (señalados por líneas rojas), mientras la humedad relativa de retorno (HuEx) apenas salió de los suyos. En el experimento en el cual se aplicó el estímulo a la válvula eléctrica, las gráficas, sobre todo las de temperatura, parecen indicar la incidencia de una perturbación de baja frecuencia, probablemente una disminución y posterior aumento de la temperatura del agua fría. Ello provocó que, aunque inicialmente la temperatura en el retorno se encontrara dentro de los límites, después se mantuviera ligeramente por debajo durante casi todo el experimento.

Con el objetivo de agilizar la etapa de estimación de parámetros, se hizo una estimación previa de los retardos basada en los coeficientes de correlación cruzada. El coeficiente de covarianza cruzada c _uy en el retardo i puede ser calculado según (1), donde ū y ȳ son las medias de las series u y y respectivamente y N es el número de observaciones. Suele ser más conveniente trabajar con la correlación cruzada adimensional r _uy , dada en (2) ^[33]. Al graficar estos últimos coeficientes para cada retardo, se puede tomar el valor del retardo con el mayor valor absoluto de r _uy como la cantidad de períodos de muestreo de retardo que hay entre la entrada y la salida ^[33]. Para la relación HuSu Vs U_V3V se estimó por este método que no existe retardo, mientras que para el resto de las relaciones se estimaron retardos de un período de muestreo. No obstante, como los modelos de función de transferencia de la Tabla 1 presentan retardos inferiores a la mitad de un período de muestreo, se consideraron en la estimación de parámetros ambas posibilidades, no tener retardo o de tener uno de un período de muestreo.

(1)

$r_{uy}\left(i\right)=\frac{c_{uy}\left(i\right)}{\sqrt{c_{uu}\left(0\right)c_{yy}\left(0\right)}}$ (2)

En el caso del preprocesamiento, a pesar de la incidencia de perturbaciones de baja frecuencia, no se consideró el filtrado, dejando que el modelo de perturbación de la estructura polinomial se encargara de este problema. Aunque no fueran muy notables las diferencias en cuanto a las magnitudes de las señales de entrada y salida, se aplicaron los métodos de escalamiento (normalización) dados por (3) y (4). El primero consiste en restarle a cada variable x su media $\overline{x}$ y dividir por su desviación estándar σ. El segundo resta a cada variable su valor mínimo $x_{\min }$ y divide el resultado por la diferencia entre sus valores máximo $x_{\max }$ y mínimo $x_{\min }$ Dado que, como se verá a continuación, se seleccionaron modelos con estructura de ruido flexible, no se consideró la eliminación de medias, offsets y tendencias lineales, ya que tiene menos impacto en la exactitud de este tipo de modelos. Luego, se tuvieron tres juegos de datos para estimar parámetros: aquellos sin preprocesamiento y los normalizados según (3) y según (4).

(3)

$x_{nm}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$ (4)

2.5.- Selección del tipo y estructura del modelo a identificar

Solo si no es posible desarrollar un modelo lineal con un número pequeño de parámetros se debe recurrir a otras opciones ^[33]. A pesar de conocerse que existen no-linealidades en el proceso estudiado, se diseñó un experimento con variaciones en las entradas que cubrieran un rango de variación usual para esas señales, según la experiencia sobre el funcionamiento del sistema. Asumiendo que en ese rango se comporta aproximadamente de manera lineal, así como que el flujo de aire permanece prácticamente constante, al ser controlado, se seleccionaron modelos lineales para representar al sistema. Luego, sobre la base del principio de superposición, se aplicaron los estímulos, buscando un modelo multivariable como se muestra en la Fig. 6.

Fig. 6 Representación del modelo multivariable de la UMA bajo el supuesto de un comportamiento lineal. 

La estructura de modelo lineal invariante en el tiempo (LTI) seleccionada fue la familia general de modelos de función de transferencia representados, en tiempo discreto, por (5) ^[32,^33]. Estos modelos, conocidos como modelos polinomiales ^[38], expresan la relación entre la entrada u(k), la salida y(k) y el ruido e(k), donde A, B, C, D y F son polinomios dados por (6) ^[31], k es el instante de tiempo discreto, nk es el retardo de tiempo (intervalos de muestreo) entre la entrada del proceso y la salida y q-1 es el operador de desplazamiento (q-1 y(k) = y(k-1)). Algunos casos especiales de modelos SISO (una sola entrada y una sola salida) pertenecientes a esta familia y utilizados con frecuencia son dados en la Tabla 2 ^[32].

$A\left(q^{-1}\right)y\left(k\right)=\frac{B\left(q^{-1}\right)}{F\left(q^{-1}\right)}u\left(k-n_k\right)+\frac{C\left(q^{-1}\right)}{D\left(q^{-1}\right)}e\left(k\right)$ (5)

$A\left(q^{-1}\right)=1+a_1{q}^{-1}+\cdots +a_{n_a}{q}^{-n_a}$$B\left(q^{-1}\right)=b_0+b_1{q}^{-1}+\cdots +b_{n_b}{q}^{-n_b}$$C\left(q^{-1}\right)=1+c_1{q}^{-1}+\cdots +c_{n_c}{q}^{-n_c}$$D\left(q^{-1}\right)=1+d_1{q}^{-1}+\cdots +d_{n_d}{q}^{-n_d}$$F\left(q^{-1}\right)=1+f_1{q}^{-1}+\cdots +f_{n_f}{q}^{-n_f}$ (6)

Tabla 2 Algunos modelos SISO de caja negra 

Polinomio utilizado	Nombre de la estructura de modelo
B A B	FIR ARX
A B C AC ABD ABCD B F B F C D	ARMAX ARMA ARARX ARARMAX OE (output error) BJ (Box-Jenkins)

2.6.- Estimación de parámetros del modelo

El procedimiento de estimación de parámetros que se utiliza selecciona el “mejor” modelo dentro de la estructura de modelo escogida ^[32]. En el caso de los modelos polinomiales se trata de, para determinada combinación de grados de los polinomios dados por (6), previamente seleccionada, estimar sus coeficientes de manera que la diferencia entre la salida del sistema y la del modelo sea la menor posible ^[38, ^40]. Para ello se hizo uso del método iterativo de predicción del error de identificación (PEM), implementado en la caja de herramientas de identificación (versión 8.3) de MatLab®. Se seleccionó la predicción como objetivo de la estimación, elección que determina cómo el error entre las salidas medida y predicha es pesado a frecuencias específicas durante la minimización de la predicción del error. En el caso del método de búsqueda para la estimación iterativa de parámetros, el algoritmo ofrecido por el software selecciona entre el método de los subespacios de Gauss-Newton, una versión adaptativa de este, el método de Levenberg-Marquardt y el método del gradiente descendente, de forma tal que la dirección descendente es calculada utilizando los anteriores métodos de manera sucesiva en cada iteración. Las iteraciones continúan hasta que es alcanzada una reducción suficiente del error.

Teniendo en cuenta las limitaciones en cuanto a la complejidad del modelo, dado el nivel de excitación en las entradas, y que se buscan modelos lo más sencillos posible, se establecieron como límites máximos para los órdenes de los polinomios dados por (6) los siguientes valores na = 1, nb = nc = 4, nd = 5, nf = 6 y nk = 1. Luego, se estimaron todos los modelos resultantes de las posibles combinaciones de los anteriores órdenes, partiendo del valor cero hasta los valores máximos fijados. Este proceso, que genera cientos de modelos, se programó al igual que parte de la validación, ya que representa un ahorro considerable de tiempo y esfuerzo con respecto a probar combinaciones de parámetros y validar los modelos resultantes uno a uno. Los modelos polinomiales fueron nombrados PM_nanbncndnfnk de acuerdo a la combinación de grados de los polinomios. Para la estimación de parámetros se hizo uso del 70 % de las muestras recolectadas del experimento con PRBS, dejando el restante 30 % para la validación.

2.7.- Validación del modelo

La validación de un modelo puede definirse como la justificación de que este posee, dentro de su dominio de aplicabilidad, un rango satisfactorio de exactitud, consistente con el uso que se le desea dar. Esta etapa de la identificación puede considerarse como un proceso dentro del proceso de desarrollo del modelo ^[41]. Como muestra la Fig. 1, el proceso de validación fue llevado a un algoritmo y luego parcialmente programado, ya que la etapa de estimación de parámetros arrojó un gran número de modelos, que se multiplicó al probar varios juegos de datos. El algoritmo propuesto para validar modelos devuelve un número relativamente pequeño de estos, entre los cuales se puede seleccionar una cantidad aún menor, de modo que exista una combinación y compromiso entre tener un conjunto pequeño de modelos, tal que la tarea de construir un controlador con un desempeño aceptable en lazo cerrado para todos los modelos sea más fácil de resolver y, a la vez, que el conjunto sea lo suficientemente grande como para incrementar la probabilidad de que el diseño sea exitoso en la vida real ^[42].

El primer criterio para validar tenido en cuenta fue el cálculo del ajuste (Fit), según (7), el cual expresa el porcentaje de la salida que el modelo reproduce ^[38], donde y es la salida medida, ŷ es la salida predicha (simulada) por el modelo, ȳ es la media de y y es aplicada la norma 2 a las diferencias y - ŷ y y - ȳ.

(7)

Como segundo criterio, se tuvieron en cuenta las ganancias de los modelos. Los experimentos realizados con entradas tipo escalón aportaron estimaciones previas de las ganancias con las que se pudieron comparar las nuevas ganancias. No obstante, es necesario tener en cuenta que las ganancias de los modelos que tienen como entrada la señal aplicada a la válvula de tres vías, dependen de la temperatura del agua fría, que, en el proceso real, en los últimos años no se ha mantenido constante. Por lo tanto, para los nuevos modelos, hallados a partir del diseño de un experimento con PRBS, no se tuvieron en cuenta las ganancias resultantes de los experimentos previos actuando sobre la válvula de tres vías. En su lugar, dado que se diseñó la PRBS con algunos pulsos lo suficientemente anchos como para estimar las ganancias, se compararon las de los modelos con las que se pudieron calcular directamente a partir de los datos de la Fig. 5. Para los modelos que tienen a la entrada la señal de control aplicada a la válvula eléctrica, sí podía esperarse que las nuevas ganancias fueran similares a las ya estimadas.

Una vez aceptado un grupo de modelos con un Fit superior a un mínimo establecido (80 %, aunque si son muchos modelos se puede tomar mayor) y con ganancias dentro de los márgenes definidos en cada caso, se calcularon los residuos, la autocorrelación entre ellos, para realizar la prueba de blancura, y la correlación cruzada con entradas pasadas, para realizar la prueba de independencia. Según la primera prueba, un buen modelo tiene la función de autocorrelación de los residuos dentro de un intervalo de confianza. De acuerdo a la segunda, un buen modelo tiene residuos no correlacionados con entradas pasadas. Evidencia de correlación indica que el modelo no describe cómo parte de la salida se relaciona con la entrada correspondiente ^[38]. Aunque lo ideal es que en ambas pruebas no se sobrepasen los intervalos de confianza, seleccionados de un 99 %, se estableció un límite de cuántos coeficientes podían sobrepasar dichos intervalos y que aun así no se descartara el modelo, que fue de uno para la correlación cruzada y de dos para la autocorrelación de los residuos.

A los modelos hasta este punto aceptados se les calcularon los ceros y polos, estableciendo igualmente límites para cuántos pueden aceptarse fuera del círculo de radio unitario. En el caso de los polos, dado que se conoce que el sistema es estable, no se aceptaron modelos con polos fuera del círculo, lo que implicaría inestabilidad. Para los ceros, se aceptó uno fuera, lo que es una posible indicación de que el sistema sea de fase no mínima, y ante un estímulo, puede que varíe, en un principio, en sentido contrario al cual finalmente llega a estabilizarse. No obstante, este comportamiento no se observó en los experimentos y tampoco al estimular los modelos con un paso. Por otra parte, los modelos con un cero fuera del círculo de radio unitario corresponden a relaciones entrada-salida donde previamente se habían detectado retardos, lo que hace muy probable que se deban a la presencia de tales retardos en los datos experimentales, que no fueron tenidos en cuenta en los modelos.

Los modelos seleccionados hasta este punto pasaron por un último filtro: la sencillez, expresada en la cantidad de parámetros del modelo. A la preselección de modelos hecha se le calculó el error de predicción final de Akaike (FPE según la literatura en inglés). Conforme a la teoría de Akaike, el modelo más exacto tiene el menor FPE ^[38]. De esta manera, se tuvieron más elementos para ayudar a elegir, dentro de los modelos preseleccionados, los mejores. La Fig. 7 muestra un ejemplo de los resultados arrojados por el algoritmo de validación. En la gráfica se observa la comparación de datos de la salida de los modelos seleccionados por este algoritmo y los datos experimentales obtenidos del proceso cuando a los modelos se les aplica el mismo estímulo que provocó la salida medida del proceso. La leyenda, además de permitir identificar a qué modelo se corresponde cada salida graficada, ofrece información valiosa como el ajuste de cada modelo a los datos experimentales, la ganancia, el FPE y la cantidad de parámetros de cada uno. En este ejemplo se evidencia cómo el algoritmo ha seleccionado una cantidad de modelos relativamente pequeña, sencillos y que describen bien el comportamiento del sistema de acuerdo a los criterios de validación mencionados anteriormente, lo que implica un ahorro de esfuerzo y tiempo durante la identificación del sistema.

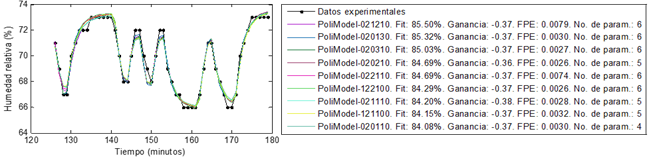
Fig 7 Ejemplo de selección de modelos para el subproceso HuSu Vs U_VE hecha por el algoritmo de validación. 

A partir de información como la mostrada en la Fig. 7, los gráficos de residuos, ceros y polos y la respuesta a un pulso, se hizo la selección, dentro de los modelos propuestos por el algoritmo de validación, de algunos para conformar el modelo multivariable de la UMA, cuyos resultados en las pruebas de validación se resumen en la Tabla 3 y las gráficas de la Fig. 9 y la Fig. 10. Puede apreciarse que uno de los modelos seleccionados no fue de una estructura específica, sino que incluyó todos los polinomios, mientras que el resto tiene estructura BJ, la mayoría, con nc = 0, lo que sugiere que esta es una estructura sencilla y exitosa a la hora de representar los subprocesos en que se descompone el proceso estudiado. También debe destacarse que, en los casos donde había modelos con algún cero fuera del círculo de radio unitario y modelos con todos los ceros dentro, se escogieron los mejores de ambos casos buscando mayores posibilidades de éxito a la hora de llevar el ajuste de los controladores a la práctica. Las letras n y nm al final de los nombres de los modelos indican si se obtuvieron con datos normalizados según (3) o según (4) respectivamente. El ajuste de los controladores y las simulaciones del sistema controlado, como prueba de validación de acuerdo al propósito de los modelos, se hicieron a partir de los modelos resaltados (sombreados) en la Tabla 3, que son los que presentan un mayor Fit. La Fig. 8 muestra la comparación de datos de estos modelos con los datos de validación de los experimentos con PRBS.

Tabla 3 Modelos seleccionados y algunos resultados en pruebas de validación 

Subproceso	Modelo	Fit	Ganancia	FPE	No. Param.	Ceros y polos
HuSu Vs U_V3V	PM_030510_nm	80.70%	-0.04	0.0065	9	Todos dentro
	PM_020520_nm	80.32%	-0.04	0.0082	9	Todos dentro
TSu Vs U_V3V	PM_010140	85.41%	-0.05	0.0094	6	Todos dentro
	PM_020130_nm	89.74%	-0.05	0.0013	6	Un cero fuera
	PM_020120_nm	89.12%	-0.05	0.0016	5	Un cero fuera
HuSu Vs U_VE	PM_110350_nm	85.07%	-0.36	0.0026	10	Todos dentro
	PM_021310_nm	85.40%	-0.36	0.0026	7	Un cero fuera
	PM_020130_nm	85.32%	-0.37	0.0030	6	Un cero fuera
TSu Vs U_VE	PM_011540_n	88.97%	0.08	0.0081	11	Todos dentro
	PM_031130	89.03%	0.08	0.0078	8	Un cero fuera

Fig. 8 Comparación de datos de los modelos seleccionados para probar un ajuste de los controladores. 

Fig. 9 Análisis de residuos. Prueba de blancura realizada a los modelos lineales obtenidos. 

Fig. 10 Análisis de residuos. Prueba de independencia realizada a los modelos lineales obtenidos. 

Tanto la Fig. 9 como la 10 son relevantes para evaluar la calidad de los modelos obtenidos. Ellas muestran los resultados del análisis de los residuos de los modelos mediante las pruebas de blancura e independencia, respectivamente. En el caso de la prueba de independencia, las gráficas de la Fig. 10 muestran que las funciones de correlación de los residuos con entradas pasadas se encuentran, en casi todos los casos, dentro del intervalo de confianza que indica que estos son estadísticamente insignificantes con una probabilidad del 99%. Solo para dos modelos ocurre que un residuo se salga, por muy poco, de su intervalo de confianza. De esta manera, en sentido general se puede afirmar que existe poca o ninguna evidencia, en la mayoría de los casos, de que las salidas de los modelos no sean adecuadamente descritas por valores pasados de sus respectivas entradas, ya que los residuos (error entre la salida predicha y la medida ^[33]) no dependen de valores pasados de las entradas. En el caso de la prueba de blancura, las gráficas de la Fig. 9 muestran que, salvo el primer juego de modelos de la Tabla 3, los demás tienen al menos un modelo en el cual no hay evidencias de autocorrelación de sus residuos y, por tanto, los residuos en un instante de tiempo no dependen (esto igualmente con una probabilidad del 99%) de los residuos en instantes anteriores.

Para las simulaciones del sistema controlado, una última y esencial prueba de validación, se utilizó, como modelo del controlador, el dado por (8), donde K _p es la ganancia proporcional, K _i es la ganancia integral (K _i = K _p /T _i , donde T _i es el tiempo de acción integral) y T _s es el período de muestreo. La selección de este modelo responde al estudio de la documentación técnica del fabricante (SIEMENS), sobre el controlador actual y otros productos, ya que para este controlador no se da un modelo matemático en dicha documentación, así como a la simulación de diferentes estructuras utilizando los parámetros actuales. La simulación se llevó a cabo en Simulink® (versión 8.2). Los resultados obtenidos con estos parámetros que mostraron un comportamiento más parecido al observado en el sistema real se correspondieron con el modelo dado en (8), el cual pertenece a un PI discreto con integración rectangular hacia atrás. De esta forma, se validaron tanto los modelos seleccionados para representar al proceso como el modelo del controlador. Para el ajuste propuesto se hizo uso de las opciones de sintonía que ofrece Simulink® a través de la interfaz de sintonía de PID y luego se realizó un ajuste fino (ver Tabla 4).

$G_{PID}\left(z\right)=K_p+K_i\frac{T_{s}z}{z-1}$ (8)

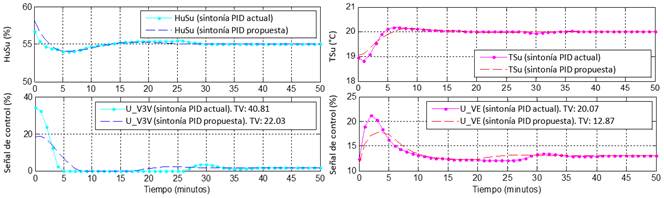
La Fig. 11 presenta un escenario de simulación en el cual se puede comparar el desempeño de los controladores con la sintonía actual y con la propuesta a la hora de llevar las variables controladas a sus referencias, lo cual es muy importante, dado que las referencias de los lazos de control PID cambian constantemente. Se puede observar como tanto para el control de temperatura como para el de humedad relativa, la respuesta del sistema controlado con la sintonía propuesta es ligeramente más estable y presenta menor sobreimpulso, aunque es un poco más lenta. Pero lo que más llama la atención de la nueva sintonía, basada en el modelo y la simulación del sistema controlado, es que el esfuerzo de control es notablemente menor, apreciable en las gráficas y en el valor del índice de desempeño TV (variación total) definido en (9) ^[43].

(9)

Para la simulación del sistema controlado, los valores iniciales de temperatura y humedad relativa fueron de 19 °C y 60 % respectivamente. En el sistema de control, mostrado en la Fig. 3, las señales de control de los controladores de temperatura por enfriamiento y por calentamiento son enviadas a las válvulas de tres vías y eléctrica respectivamente, mientras el controlador de humedad relativa establece el mínimo valor para la saturación de la salida del controlador de temperatura por enfriamiento. Se tuvieron en cuenta las interacciones entre variables, como se muestra en el modelo multivariable de la UMA de la Fig. 6, tanto para el ajuste de los controladores como para las simulaciones, cuyos resultados se muestran en la Fig. 11.

Tabla 4 Sintonía actual y propuesta para los controladores 

Controlador	Referencia	Acción	Parámetros	Sintonía actual	Sintonía propuesta
Temperatura	21 °C	Directa	Kp	5	8.438
(enfriamiento)			Ti (seg)	180	0.146
Temperatura	20 °C	Inversa	Kp	7	7.000
(calentamiento)			Ti (seg)	40	1.400
Humedad	55 %	Directa	Kp	5	3.000
relativa			Ti (seg)	180	1.000

Fig. 11 Resultados de la resintonía de los controladores PID y comparación con la sintonía actual 

Conclusiones

La dificultad del desarrollo de modelos de las UMAs basados en leyes físicas, por la naturaleza compleja de los sistemas térmicos y la gran cantidad de parámetros que presentan, que no siempre se pueden conocer, hacen atractiva la vía experimental para este propósito. Por otra parte, la aplicación de la identificación de sistemas en un caso real de la industria puede ser un proceso trabajoso y demorado. En ello pueden influir el tiempo necesario para la experimentación, las dificultades derivadas de la adquisición y calidad de los datos y lo tedioso que llegue a ser la estimación de parámetros, que involucra un proceso de prueba y error en la selección de las estructuras de modelo y sus parámetros. Este trabajo mostró la posibilidad de identificar modelos buenos (rigurosamente validados) y simples de una UMA, en un tiempo relativamente corto y con menos esfuerzo, al aplicar la metodología de la identificación tal cual se propone, además de hacerlo de manera segura. La clave para esto radicó en el estudio del proceso, las opciones de pretratamiento de los datos más adecuadas de conjunto con la selección por parte del algoritmo programado de los mejores modelos, reduciendo el trabajo humano a solo limitar la complejidad de la estructura seleccionada y el rigor o flexibilidad de las pruebas de validación propuestas.

El trabajo realizado defiende el uso de modelos lineales en la representación de los subprocesos de variación de la temperatura y la humedad relativa en la UMA estudiada, donde se concluye que la estructura BJ es una buena opción para capturar su dinámica. La última prueba de validación realizada fue una muestra de lo ventajoso de ajustar los controladores sobre la base del modelo. Para ganar en capacidad de extrapolación y que se reflejen adecuadamente las no-linealidades del proceso, se propone, en futuros estudios, realizar experimentos de identificación utilizando señales pseudoaleatorias de amplitud variable o multiniveles como estímulos, que permitan obtener tanto modelos de caja negra como modelos de caja gris. Estos últimos, a partir del uso de las leyes físicas conocidas que describen algunos de los subsistemas que componen el sistema estudiado, como, por ejemplo, el intercambio de calor en el serpentín de agua fría.

Referencias

1.  Yan X, Guo P, Zhang S, Yan X, Liu C. Static pressure set-point reset smoothing scheme based-on improved iterative learning control and variable trajectory for air-conditioning system. Journal of Process Control. 2020;91:63-71.

2.  Xiong W, Wang J. A semi-physical static model for optimizing power consumption of HVAC systems. Control Engineering Practice [Internet]. 2020 2020 mar 2020 nov 24]; 96. Available from: www.sciencedirect.com/science/article/abbs/pii/S096670661203000832.  .

3.  Shah A, Huang D, Chen Y, Kang X, Qin N. Robust Sliding Mode Control of Air Handling Unit for Energy Efficiency Enhancement. Energies. 2017;10(11):1-21.

4.  Moradi H, Vossoughi G. Multivariable control of the bifurcation and harmonic perturbations to improve the performance of air-handling units. ISA Transactions. 2016;60:119-27.

5.  Afram A, Janabi-Sharifi F. Black-box modeling of residential HVAC system and comparison of gray-box and black-box modeling methods. Energy and Buildings. 2015;94:121-49.

6.  Müller G, Sugiyama H, Stocker S. Reducing Energy Consumption in Pharmaceutical Production Processes: Framework and Case Study. J Pharm Innov. 2014;9:212-26.

7.  Mustafaraj G, Chen J, Lowryb G. Development of room temperature and relative humidity linear parametric models for an open office using BMS data. Energy and Buildings. 2010;42:348-56.

8.  Fernández E, Díaz A, Torres K. Identificación de la temperatura y la humedad relativa en una unidad manejadora de aire. Revista Cubana de Ingeniería. 2013;IV(1):15-22.

9.  Homod RZ, Sahari KSM, Almurib HAF, Nagi FH. Double cooling coil model for non-linear HVAC system using RLF method. Energy and Buildings 2011;43(9):2043-54.

10.  Zajic I, Larkowski T, Sumislawska M, Burnham KJ, Hill D. Modelling of an air handling unit: a Hammerstein-bilinear model identification approach. 21st International Conference on Systems Engineering; 16-18 ago 2011; Las Vegas, NV, USA. 2011 21st International Conference on Systems Engineering: IEEE 2011. p. 53-69.

11.  Goyal S, Barooah P. A method for model-reduction of non-linear thermal dynamics of multi-zone buildings. Energy and Buildings. 2012;47:332-40.

12.  Pacheco J, Rubio JdJ, Hernandez JA, Medina A, Lopez A, Zacarias A. Modeling of a HVAC System for Clean Rooms. IEEE LATIN AMERICA TRANSACTIONS. 2018;16(3):829-38.

13.  Schito E. Dynamic simulation of an air handling unit and validation through monitoring data. Energy Procedia. 2018;148:1206-13.

14.  Talib R, Nabil N, Choi W. Optimization-Based Data-Enabled Modeling Technique for HVAC Systems Components. Buildings [Internet]. 2020; 10(9).

15.  Moradi H, Saffar-Avval M, Bakhtiari-Nejad F. Nonlinear multivariable control and performance analysis of an air-handling unit. Energy and Buildings. 2011;43:805-13.

16.  Moradi H, Bakhtiari-Nejad F, Saffar-Avval M. Multivariable robust control of an air-handling unit: A comparison between pole-placement and H∞ controllers. Energy Conversion and Management. 2012;55:136-48.

17.  Moradi H, Setayesh H, Alasty A. PID-Fuzzy control of air handling units in the presence of uncertainty. International Journal of Thermal Sciences. 2016;109:123-35.

18.  Homod RZ, Gaeid KS, Dawood SM, Hatami A, Saharie KS. Evaluation of energy-saving potential for optimal time response of HVAC control system in smart buildings. Applied Energy. 2020;271:115-225.

19.  Homod RZ, Sahari KSM. Energy savings by smart utilization of mechanical and natural ventilation for hybrid residential building model in passive climate. Energy and Buildings. 2013;60:310-29.

20.  Homod RZ. Assessment regarding energy saving and decoupling for different AHU (air handling unit) and control strategies in the hot-humid climatic region of Iraq. Energy. 2014;74:762-74.

21.  Santoro BF, Rincón D, Silva VCd, Mendoza DF. Nonlinear model predictive control of a climatization system using rigorous nonlinear model. Computers and Chemical Engineering. 2019;125:365-79.

22.  Sun Z, Wang S, Zhu N. Model-based Optimal Control of Outdoor Air Flow Rate of an Air-Conditioning System with Primary Air-Handling Unit. Indoor Built Environ. 2011;20(6):626-37.

23.  Goyal S, Barooah P. Energy-efficient control of an air handling unit for a single-zone VAV system.52nd IEEE Conference on Decision and Control; Florence, Italy 2013. p. 4796-801.

24.  Razban A, Khatib A, Goodman D, Chen J. Modelling of air handling unit subsystem in a commercial building. Thermal Science and Engineering Progress. 2019;11:231-8.

25.  Khan MW, Choudhry MA, Zeeshan M. Adaptive fuzzy multivariable controller design based on genetic algorithm for an air handling unit. Energy. 2015;81:477-88.

26.  Setayesh H, Moradi H, Alasty A. A comparison between the minimum-order and full-order observers in robust control of the air handling units in the presence of uncertainty. Energy and Buildings. 2015;91:115-30.

27.  Schwingshackl D, Rehrl J, Horn M. LoLiMoT based MPC for air handling units in HVAC systems. Building and Environment. 2016;96:250-9.

28.  Abdo-Allah A, Iqbal T, Pope K. Modeling, Analysis, and Design of a Fuzzy Logic Controller for an AHU in the S.J. Carew Building at Memorial University. Journal of Energy [Internet]. 2018 19 nov 2020 24 nov 2020]; 2018:[1-11 pp.]. Available from: www.hindawi.com/journals/jen/2018/454038728.  .

29.  Joe J, Im P, Dong J. Empirical Modeling of Direct Expansion (DX) Cooling System for Multiple Research Use Cases. Sustainability [Internet]. 2020; 12(20). Available from: http://doi.org/10.3390/su1220873829.  .

30.  Zaki MU, Mishra DP. Overview of HVAC System: Operational Significance of HVAC Provision for Pharmaceutical Facilities. International Journal on Recent and Innovation Trends in Computing and Communication. 2015;3(3):1261-7.

31.  Galitsky C, Worrell E, Masanet E, Chang S-c. Improving Energy Efficiency in Pharmaceutical Manufacturing Operations -- Part II: HVAC, Boilers and Cogeneration2006 24 nov 2020 [cited 2020 24 nov 2020]:[8 p.]. Available from: Available from: https://escholarship.org/uc/item/91b1k118 31.  .

32.  Ljung L. System Identification. Theory for the User. 2 ed. Kailath T, editor. Upper Side River, NJ 074581999.

33.  Roffel B, Betlem B. Process Dynamics and Control. Modeling for Control and Prediction. The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England: John Wiley & Sons Ltd; 2006.

34.  Isermann R, Munchhof M. Identification of Dynamic Systems. An Introduction with Applications. Heidelberg: Springer; 2011.

35.  Ghiaus C, Chicinas A, Inard C. Grey-box identification of air-handling unit elements. Control Engineering Practice. 2007;15:421-33.

36.  Lorenzo WT. Control avanzado en sistema de HVAC de Planta II del Instituto Finlay: Instito Superior Pilitécnico José Antonio Echeverría; 2014.

37.  Yu C, Wang Q-G, Zhang D, Wang L, Huang J. System Identification in Presence of Outliers. IEEE Transactions on Cybernetics. 2016;46(5):1202-16.

38.  Ljung L. System identification toolbox™ user's guide. Natick: The MathWorks, Inc.; 2015.

39.  Forssell U, Ljung L. Identification of Unstable Systems Using Output Error and Box-Jenkins Model Structures. IEEE TRANSACTIONS ON AUTOMATIC CONTROL. 2000;45(1):137-41.

40.  Mikleš J, Fikar M. ProcessModelling, Identification, and Control. Heidelberg: Springer; 2007.

41.  Sargent RG. Verification and validation of simulation models. Journal of Simulation. 2013;7(1):12-24.

42.  Ljung L. Model Validation and Model Error Modeling. Linköping University Engineering DoE; 1999LiTH-ISY-R-2125.

43.  Yero GG, Mendoza MR, Martí LM. Un nuevo método de control PI no lineal robusto. RIELAC. 2017;XXXVIII:1-16.

Recibido: 12 de Julio de 2020; Aprobado: 30 de Abril de 2021

^*Autor para la correspondencia: [e-mail]

Ninguno de los autores manifestó la existencia de posibles conflictos de intereses que debieran ser declarados en relación con este artículo.

Carlos Alberto García Vázquez: Investigación, curación de datos, análisis formal, metodología, recursos, software, validación-verificación, visualización, redacción-borrador original y edición.

Ana Isabel González Santos: Conceptualización, metodología, recursos, administración del proyecto, supervisión, validación-verificación, visualización, redacción-revisión y edición.

Víctor Pérez Garrido: Investigación, metodología, recursos.