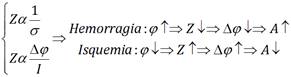1.- Introducción
Las enfermedades cerebrovasculares (ECV) ocupan uno de los primeros lugares entre las principales causas de muerte a nivel mundial. Esta enfermedad ostenta, además, el primer lugar como patología neurológica invalidante prevalente en personas mayores de 65 años [1]. De ahí que se considere como uno de los principales problemas de salud en países donde es típica una larga expectativa de vida y como consecuencia, existe una población envejecida [2, 3, 4]. El principal reto al que se enfrenta la asistencia médica, cuyo objetivo es realizar una intervención terapéutica oportuna que disminuya la mortalidad y morbilidad, es realizar un diagnóstico diferencial preciso en la fase inicial de esta (fase aguda o subaguda) [5].
Para abordar esta problemática los protocolos que se aplican en la actualidad establecen el uso de técnicas imagenológicas para confirmar el diagnóstico clínico [6, 7], y diferenciar la variante isquémica de esta enfermedad, la cual tiene mayor incidencia [8, 9], de la variante hemorrágica. Las técnicas más comunes son la Tomografía Computarizada (TC) y la Resonancia Magnética Nuclear (RMN) [10, 11]. En el caso de TC, esta tiene una gran sensibilidad para detectar la presencia de una hemorragia cerebral, pero generalmente, en las primeras horas de ocurrida una ECV isquémica, esta puede ser normal, por lo que no se puede descartar su presencia. En el caso de la RMN, aunque tiene una mayor sensibilidad que la TC para detectar precozmente la ECV isquémica [12], presenta como desventaja que requiere un mayor tiempo para realizar el estudio, además, está contraindicada en portadores de marcapasos, implantes metálicos, pacientes con claustrofobia y que padezcan de obesidad mórbida.
Para alcanzar una mayor sensibilidad en el diagnóstico precoz se pueden emplear la Tomografía Computarizada Funcional (TCF), la Imagen por Resonancia Magnética funcional (IRMf), la Tomografía Computarizada de Emisión Monofotónica (SPECT), las técnicas de neuroimágenes multimodales: la TC de perfusión, la Resonancia Magnética (RM) de difusión y perfusión, los estudios de imágenes vasculares por medio de Doppler Transcraneal, angio-TC y la angio-RM [13, 14]. Estas técnicas son costosas y no están siempre disponibles en las instituciones hospitalarias, por lo que obtener estas imágenes en las primeras 24 horas no siempre es posible, influyendo en la tasa de tratamiento que es en promedio del 4% en este lapso de tiempo [15].
Las técnicas de imágenes están bien establecidas en la clínica y contribuyen al diagnóstico, sin embargo, no son adecuadas para el monitoreo cerebral continuo, debido a su baja resolución temporal, o aplicables en algunas situaciones críticas [14]. Otros métodos, como la medición de la presión intracraneal son invasivos y por tanto, aumentan el riesgo de daño cerebral, por lo que solo se usan en situaciones muy específicas [16].
La técnica de bioimpedancia eléctrica cerebral, en la cual la información respecto a las propiedades eléctricas intrínsecas de los tejidos bilógicos es obtenida por medio de la aplicación de una corriente eléctrica en el tejido y la medición de los potenciales eléctricos en la superficie, generados por la circulación de esta, contiene potencialidades para convertirse en una variante de monitoreo de daño cerebral. En relación a esta técnica, se han empleado varias de sus modalidades para el seguimiento de lesiones cerebrales: la Bioimpedancia Eléctrica (EBI) básica [17], la Espectroscopia de Impedancia Eléctrica (EIS) [18] y la Tomografía de Impedancia Eléctrica (EIT) [19].
Se ha mostrado que el daño cerebral provocado por la ECV, isquémica o hemorrágica, usualmente es unilateral, es decir, se encuentra localizado en un solo hemisferio cerebral [9]. Se ha mostrado también que en seres humanos normales no existen diferencias significativas en cuanto a valores de impedancia eléctrica entre hemisferios suponiendo dos hemisferios cerebrales simétricos, sin embargo la ECV incrementa significativamente esas diferencias [15, 20, 21].
En el caso de lesiones unilaterales, las cuales son las consideradas en este trabajo, las asimetrías eléctricas provocadas por las ECV entre hemisferios cerebrales pueden emplearse para determinar el tipo de lesión, su tamaño y posición aproximados, lo cual es relevante en el entorno del diagnóstico diferencial precoz y el monitoreo de esta enfermedad [15]. Una buena referencia en la que fueron obtenidas evidencias de estas potencialidades es el trabajo publicado por Cohen y col. en [21], los cuales empleando un modelo numérico de cabeza 3D evaluaron el efecto producto de variaciones en la conductividad eléctrica y las dimensiones del tejido cerebral dañado en la asimetría entre hemisferios cerebrales a partir de la EBI. Sin embargo, los índices de asimetría utilizados por ellos no permiten la localización de la lesión dentro del hemisferio dañado, a menos que sean conocidos a priori los valores iniciales (normales) de tales índices para cada posición explorada, o se realice una tomografía, lo que acarrea la implementación de algoritmos de reconstrucción de imágenes que son matemáticamente dificultosos y desafiantes.
Un problema adicional en este tipo de estudio es que existe la tendencia a emplear modelos numéricos de cabeza en los cuales se trata de obtener una representación más realista del fenómeno bajo estudio incorporando más estructuras cerebrales, como en [20, 21], lo cual implica que se requiera mucha más potencia de procesamiento, siendo típico el uso de superordenadores, mayores tiempos de ejecución de los experimentos, generalmente más de 24 horas por cada corrida del modelo, todo esto aparejado a una optimización y un ajuste preciso del solucionador empleado.
En este trabajo se analizan las potencialidades y la viabilidad de la EBI para el diagnóstico diferencial y el monitoreo de la ECV mediante modelación numérica basada en el método de los elementos finitos, para lo cual se construyó un modelo hemisférico del cerebro humano de 4 capas: cuero cabelludo, cráneo, líquido cefalorraquídeo y tejido cerebral. Con tal objetivo se desarrolló un biomarcador basado en el índice de asimetría eléctrica, el cual además de permitir diferenciar las variantes isquémica y hemorrágica de la ECV, permite determinar la localización aproximada de la región dañada dentro del hemisferio dañado sin la necesidad de conocer a priori los valores iniciales para cada posición, permitiendo así un monitoreo de la lesión más confiable. Los resultados obtenidos evidencian la posibilidad de desarrollar un nuevo método complementario para el diagnóstico diferencial y el monitoreo de la ECV.
2.- Materiales y Métodos
2.1.- Solución de la Ecuación de Laplace
La implementación de la técnica de bioimpedancia en el modelo numérico emplea la inyección de una corriente eléctrica de 1 mA de forma diametral a través una pareja de electrodos posicionados en el nasion y en el inion, determinándose la diferencia de potencial eléctrico en parejas de electrodos adyacentes preestablecidas.
Para determinar esta diferencia de potencial se resolvió la ecuación de Laplace para el potencial eléctrico
A partir de
donde
En la frontera exterior del modelo se aplicó la condición de frontera de aislamiento eléctrico, es decir,
El solucionador de elementos finitos usado (FGMRES) está basado en el método de residuos mínimos generalizados flexible. Este es un solucionador iterativo para sistemas no simétricos de ecuaciones lineales el cual emplea métodos del espacio de Krylov. El mismo fue escogido debido a que es un solucionador iterativo rápido para ecuaciones lineales y además es apropiado en general para matrices no simétricas. Además genera una solución convergente minimizando la norma euclidiana de los residuos del sistema con cada ciclo iterativo. Las simulaciones fueron realizadas en una PC dotada de un procesador Intel(R) Core (TM) i3 4150 CPU @ 3.50 GHz y una memoria RAM de 16 GHz, tomando típicamente cerca de 3 min la obtención de la solución en cada una de las corridas.
2.2.- Modelo FEM de cabeza humana
La Fig. 1 muestra el modelo de elementos finitos 3D hemisférico construido y usado en las simulaciones. Un modelo similar fue usado por Towers y col. en [22] para la investigación de los requerimientos de sensibilidad de un sistema de Tomografía de Impedancia Eléctrica cerebral, obteniendo resultados realistas.

Figura 1 Modelo usado en las simulaciones de elementos finitos con 16 electrodos sobre el cuero cabelludo. El electrodo 8 está posicionado en el nasion y el electrodo 16 está posicionado en el inion.
La geometría esférica del modelo fue seleccionada debido a que el cerebro humano es aproximadamente de forma hemisférica y se sostiene por una estructura ósea que conduce pobremente la corriente eléctrica. El modelo de la cabeza tiene un radio exterior de 100 mm y comprende regiones concéntricas de tejido cerebral (σ=0.27 S/m) [23], fluido cerebroespinal (σ=1.79 S/m) [23], cráneo (σ=0.018 S/m) [24, 25], y cuero cabelludo (σ=0.19 S/m) [25]. El fluido cerebroespinal (FCE), el cráneo y el cuero cabelludo tienen espesores de 1.5 mm, 8 mm y 3 mm, respectivamente. Las dimensiones geométricas del modelo son iguales a las usadas por Towers y col. en [22], mientras que para la conductividad eléctrica de los cuatro compartimentos se usaron valores más realistas, correspondientes a los de los tejidos dentro del cuerpo vivo [26].
Igual que en [22], dieciséis electrodos de cobre de dimensiones 10 mm x 10 mm x 2 mm fueron ubicados equidistantemente alrededor del plano pseudo-ecuatorial del hemisferio sobre la superficie del cuero cabelludo y tampoco se consideró el efecto de la impedancia de contacto electrodo-piel. Para la realización de este trabajo el solucionador fue configurado con un mallado tetraédrico lo suficientemente refinado (alrededor de 1.4×106 elementos) para la obtención de la solución del potencial eléctrico con un error residual normalizado de 5×10-12, mucho menor que el de Towers y col. en [22] (1×10-8).
2.3.- Modelación del daño cerebral
En una ECV isquémica la despolarización de las neuronas causa la activación de los canales de calcio (activados por potencial eléctrico) y el lanzamiento al espacio extracelular de aminoácidos excitatorios debido a un déficit local de energía. El glutamato en particular, que en condiciones energéticas normales es absorbido pre-sinápticamente inmediatamente, o a través de los astrocitos, ahora permanece remanente en el espacio extracelular donde se acumula dramáticamente provocando el aumento del nivel de calcio intracelular. Por otro lado, la sobreactivación de los receptores de glutamato causa un aumento en las concentraciones de sodio y cloro [27]. Todos estos procesos provocan una perturbación masiva en la homeostasis iónica, acompañada de un influjo de agua pasivo y edema celular. Estas perturbaciones a nivel molecular se traducen luego en alteraciones a nivel celular, y a su vez a nivel de tejido, las cuales generan cambios en la actividad y en las propiedades eléctricas del tejido cerebral.
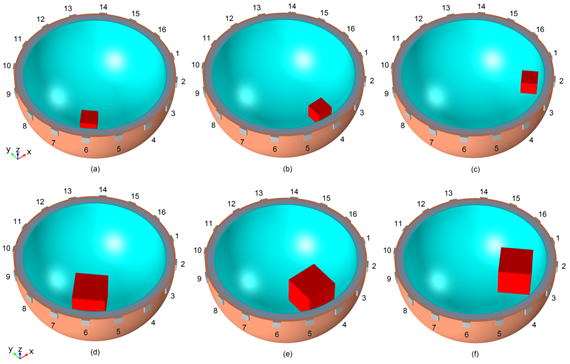
Figura 2 Lesiones localizadas en el hemisferio derecho, de tamaño 1 en las regiones frontal (a), temporal (b) y occipital (c) y de tamaño 2 en las regiones frontal (d), temporal (e) y occipital (f). Para su visualización se ha ocultado el tejido cerebral.
El experimento realizado consistió en recrear en el modelo las alteraciones en el potencial eléctrico que pueden ser registradas en el cuero cabelludo, producidas por lesiones isquémicas y hemorrágicas unilaterales de tamaños pequeño y grande representativos, e investigar estas mediante un índice de asimetría eléctrica que permita determinar la localización aproximada de la región dañada dentro del hemisferio dañado, sin la necesidad de conocer a priori los valores iniciales de este para cada posición o de realizar una tomografía de impedancia eléctrica. Con tal objetivo se modeló el daño cerebral variando la conductividad eléctrica de una región del cerebro específica y las dimensiones de dicha región. Se siguió la lógica experimental desarrollada por Cohen y col. en [21].
Igual que en [22], la lesión fue modelada como una región cúbica en el hemisferio derecho. Se consideraron lesiones localizadas en las regiones frontal (F), temporal (T) y occipital (O), de dos tamaños diferentes, tamaño 1 → 8 cm3, tamaño 2 → 64 cm3. Dichos valores corresponden a dimensiones típicas en los extremos inferior y superior de lesiones producidas por esta enfermedad, los cuales han sido determinados por métodos imagenológicos.
A la lesión hemorrágica sin tratamiento se le asignó una conductividad igual a la de la sangre (σ=0.7 S/m), valor representativo utilizado comúnmente en este tipo de investigación [15, 19, 20, 21, 29, 30, 31, 32, 33], mientras que a la lesión isquémica sin tratamiento se le asignó una conductividad igual a la de las placas de ateroma (σ=0.07 S/m), que es una de las conductividades más bajas de las placas aórticas humanas encontradas por otros autores y fue el valor utilizado por Cohen y col. en [21]. La Fig. 2 muestra las posiciones y las dimensiones de las lesiones insertadas en el volumen cerebral.
2.4.- Potenciales eléctricos e índices de asimetría hemisférica
La implementación de la técnica de bioimpedancia en el modelo comprende la inyección diametral de una corriente de 1 mA a través de los electrodos 8 y 16, Fig. 3, y la determinación de las diferencias de potencial entre pares de electrodos producto de esta excitación.
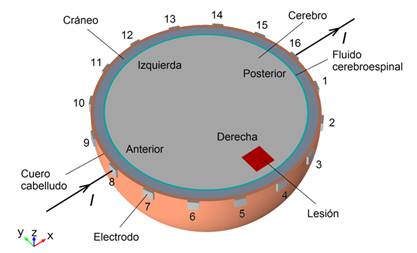
Figura 3 Inyección diametralmente en el modelo de una corriente de 1 mA a través de los electrodos 8 (nasion) y 16 (inion).
En base a los potenciales eléctricos
Donde φ es el valor absoluto o amplitud del potencial eléctrico complejo <math> <mover accent='true'><mi>φ</mi><mo>˜</mo> </mover> </math>, y los subíndices m, n, p, q denotan los electrodos involucrados.
El índice A RL fue concebido para ser evaluado cuando la lesión está localizada en el hemisferio derecho, mientras que el índice A LR , para ser evaluado cuando la lesión está localizada en el hemisferio izquierdo. En ambos casos las diferencias de potencial φ m ( φ n se determinan sobre el hemisferio derecho, mientras que las φ p ( φ q se determinan sobre el hemisferio izquierdo, debiendo ambas ser positivas, lo cual determina el sentido en que estas deben ser tomadas.
Los valores obtenidos de A RL se asociaron a las posiciones de los electrodos 1···8 y se ordenaron convenientemente como se muestra en la Tabla 1. El grupo formado fue usado para la prueba de asimetría, la cual consiste en la comparación de los índices de asimetría hemisférica obtenidos para las posiciones de los electrodos involucradas, tanto para la variante isquémica como para la hemorrágica de esta enfermedad.
Tabla 1 Índices de asimetría A RL usados para la detección del daño cerebral
| Índice de asimetría hemisférica | Subíndice del electrodo | Posición | |||
| ARL | m | n | p | q | |
|
|
1 | 16 | 15 | 16 | 1 |
|
|
2 | 1 | 14 | 15 | 2 |
|
|
3 | 2 | 13 | 14 | 3 |
|
|
4 | 3 | 12 | 13 | 4 |
|
|
5 | 4 | 11 | 12 | 5 |
|
|
6 | 5 | 10 | 11 | 6 |
|
|
7 | 6 | 9 | 10 | 7 |
|
|
8 | 7 | 8 | 9 | 8 |
3.- Resultados
La Fig. 4 muestra la distribución del potencial eléctrico y de la densidad de corriente para el modelo en su variante de un sujeto sano y para un sujeto con una ECV hemorrágica.
Las Figs. 4(a) y 4(b) muestran la distribución de las líneas equipotenciales del potencial eléctrico y el campo vectorial de densidad de corriente en un modelo sano (a) y un modelo hemorrágico (b), respectivamente. Las Figs. 4(c) y 4(d) muestran la distribución de las isolíneas de densidad de corriente y de la densidad de corriente en escala logarítmica en los modelos antes mencionados.
En el modelo de un sujeto sano, Fig. 4(a), las líneas equipotenciales son simétricas con relación al plano sagital medio y producen gradientes de potencial similares alrededor de las parejas de electrodos simétricas con relación al plano sagital medio de la cabeza, es decir, 7-9, 6-10, 5-11, 4-12, 3-13, 2-14 y 1-15, pero esta simetría se pierde en las parejas frontales del modelo hemorrágico, Fig. 4(b) .
La lesión hemorrágica crea un gradiente de potencial diferente en las cercanías del electrodo 6 en comparación con el control sano y con su contraparte en el hemisferio izquierdo (las cercanías del electrodo 10). Sin embargo, el gradiente de potencial en las cercanías de las parejas de electrodos más distantes de la lesión permanece simétrico.
En el modelo del sujeto sano, Fig. 4(c), las isolíneas de la densidad de corriente son simétricas con relación al plano sagital medio y producen gradientes de la densidad de corriente similares alrededor de las parejas de electrodos simétricas con relación al plano sagital medio de la cabeza, es decir, 7-9, 6-10, 5-11, 4-12, 3-13, 2-14 y 1-15, pero al igual que en el caso del potencial eléctrico esta simetría se pierde en las parejas frontales del modelo hemorrágico, Fig. 4(d).
La lesión hemorrágica crea un gradiente de densidad de corriente diferente en las cercanías del electrodo 6 en comparación con el control sano y con su contraparte en el hemisferio izquierdo (las cercanías del electrodo 10). Sin embargo, el gradiente de densidad de corriente en las cercanías de las parejas de electrodos más distantes de la lesión permanece simétrico. Se puede notar en la Fig. 4 que en ambos casos, en el modelo numérico de cabeza de un sujeto sano, Fig. 4(c), y en el modelo de un sujeto con hemorragia, Fig. 4(d), las mayores densidades de corrientes se generan en el entorno de los electrodos 8 y 16, a través de los cuales se hace circular la corriente por el modelo, mientras que las menores densidades de corriente se generan en las cercanías de los electrodos laterales centrales. Esto es una consecuencia del principio físico según el cual la corriente circula con mayor facilidad por el camino que le ofrece la menor resistencia.
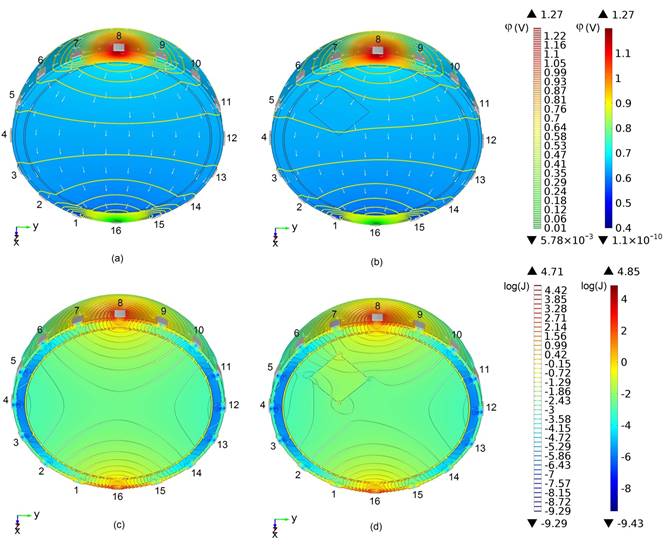
Figura 4 Distribución del potencial eléctrico y de la densidad de corriente en el modelo de un sujeto sano [(a) y (c), respectivamente] y de un sujeto con una ECV hemorrágica frontal de tamaño 2 [(b) y (d), respectivamente].
Los resultados presentados hasta aquí están en plena concordancia con los resultados reportados por Seoane y col. en [17], según los cuales las patologías neurológicas modifican la composición dieléctrica de la cabeza, produciendo cambios que pueden ser detectados por la EBI. Están en concordancia también con los resultados reportados por Cohen y col. en [21], donde las simulaciones usando un modelo numérico de cabeza humana realista revelaron que la conductividad eléctrica y el tamaño del tejido dañado tienen un efecto sobre la asimetría del potencial eléctrico superficial. Asimismo, concuerdan con los resultados reportados por Atefi y col. en [20], los cuales usando un modelo numérico de cabeza realista observaron que una hemorragia intracraneal esférica de 25.3 cm3, localizada en el lóbulo frontal izquierdo del cerebro, cerca del electrodo F7, afectó la distribución del potencial eléctrico superficial en esa región: las líneas equipotenciales del modelo sano eran simétricas con relación al plano sagital medio y producían gradientes de potencial alrededor de las parejas de electrodos ubicadas simétricamente con relación a dicho plano (F7-F8, C3-C4 y P7-P8), pero esa simetría se perdía en la pareja frontal (F7-F8) del modelo con el tejido dañado.
La Fig. 5 muestra los valores del índice de asimetría hemisférica en las posiciones 1…8, de acuerdo con la Tabla 1, para una hemorragia cerebral de tamaño 1, Fig. 5(a), (b) y (c), localizadas en las regiones frontal, temporal y occipital, respectivamente, (ver Fig. 2), y para lesiones de tamaño 2, Fig. 5(d), (e) y (f) , localizadas en las mismas regiones.
Como se puede apreciar, en el caso de lesiones frontales y temporales el índice de asimetría alcanza un valor máximo en las cercanías del electrodo más cercano a la lesión, mientras que en el caso de lesiones occipitales el índice de asimetría alcanza un valor máximo en las cercanías del electrodo adyacente a la lesión que se encuentra más alejado del sumidero de corriente, es decir, del electrodo 16.
Se puede notar que para las tres localizaciones de la lesión hemorrágica el índice de asimetría es positivo en el entorno de la misma, lo cual está en concordancia con lo reportado por Cohen y col. en [21] usando un modelo numérico de cabeza 3D realista y por Jieshi y col. en [28], usando un modelo numérico de cabeza 2D y un modelo físico de cabeza 3D realista. El índice de asimetría para las lesiones de tamaño 2 es mayor que para una lesión de tamaño 1 (aproximadamente 2.9 veces para las lesiones frontales y occipitales y aproximadamente 4.0 veces para las lesiones temporales).

Figura 5 Índices de asimetría hemisférica obtenidos de las simulaciones del potencial eléctrico para el modelo de cabeza humana de un sujeto con una lesión cerebrovascular hemorrágica de tamaño 1 [(a), (b) y (c)] o de tamaño 2 [(d), (e) y (f)], localizada en la región frontal [(a) y (d)], temporal [(b) y (e)] u occipital [(c) y (f)].
La Fig. 6 muestra los valores del índice de asimetría hemisférica en las posiciones 1…8, de acuerdo con la Tabla 1, para una isquemia cerebral de tamaño 1, Fig. 5(a), (b) y (c), localizadas en las regiones frontal, temporal y occipital, respectivamente, (ver Fig. 2), y para lesiones de tamaño 2, Fig. 5(d), (e) y (f), localizadas en las mismas regiones.
Como se puede apreciar, al igual que para las lesiones hemorrágicas, en el caso de lesiones isquémicas frontales y temporales el índice de asimetría alcanza un valor mínimo en las cercanías del electrodo más cercano a la lesión, mientras que en el caso de lesiones isquémicas occipitales el índice de asimetría alcanza un valor mínimo en las cercanías del electrodo adyacente a la lesión que se encuentra más alejado del sumidero de corriente. Se puede notar que para las tres localizaciones de la lesión isquémica el índice de asimetría es negativo en el entorno de la misma, lo cual está en concordancia con lo reportado por Cohen y col. en [21], usando un modelo numérico de cabeza 3D realista.
Para las tres localizaciones de la lesión isquémica el índice de asimetría es negativo en el entorno de la misma y su valor absoluto es mayor que para una lesión de tamaño 1 (aproximadamente 2.8 veces para las lesiones frontales y occipitales y aproximadamente 3.9 veces para las lesiones temporales).
El valor asignado a la conductividad de la lesión isquémica en las simulaciones anteriores (0.07 S/m) constituye un valor extremo que pudiera alcanzarse después de las 4-5 horas del inicio del ictus según se infiere de los resultados de Van Harreveld y col. en [34]. En la Fig. 7 (a) se muestran los índices de asimetría hemisférica obtenidos de las simulaciones del potencial eléctrico para el modelo de cabeza humana de un sujeto con una lesión cerebrovascular isquémica de tamaño 1 con una conductividad eléctrica de 0.13 S/m, localizada en la región temporal, valor que pudiera alcanzarse alrededor de los 6 min del inicio del ictus, considerando un valor inicial de la conductividad igual a la del tejido cerebral normal (0.27 S/m). Comparando los resultados mostrados en la Fig. 7 (a) con los de la Fig. 6 (b) se puede ver que los índices de asimetría disminuyen aproximadamente en la misma proporción en que aumenta la conductividad de la lesión.
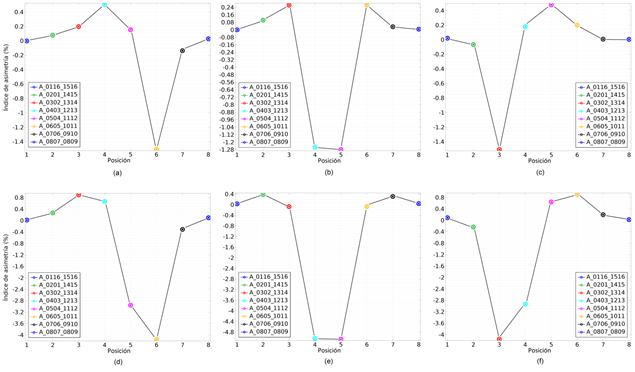
Figura 6 Índices de asimetría hemisférica obtenidos de las simulaciones del potencial eléctrico para el modelo de cabeza humana de un sujeto con una lesión cerebrovascular isquémica de tamaño 1 [(a), (b) y (c)] o de tamaño 2 [(d), (e) y (f)], localizada en la región frontal [(a) y (d)], temporal [(b) y (e)] u occipital [(c) y (f)].
En la Fig. 7(b) se muestran los índices de asimetría hemisférica obtenidos de las simulaciones del potencial eléctrico para el modelo de cabeza humana de un sujeto con una lesión cerebrovascular hemorrágica de tamaño 1, localizada en la región temporal frente al electrodo 4, adyacente a una lesión cerebrovascular isquémica de tamaño 1 con una conductividad eléctrica de 0.07 S/m, localizada en la región temporal-frontal frente a los electrodos 5 y 6. Como se puede ver, en un caso como este, poco probable pero posible, el índice de asimetría definido permite diferenciar la región hemorrágica de la isquémica. Sin embargo, si las lesiones hemorrágica e isquémica estuvieran alineadas radialmente, cabe la posibilidad de que sus efectos sobre el índice de asimetría se anulen y en ese caso no podrían ser detectadas.
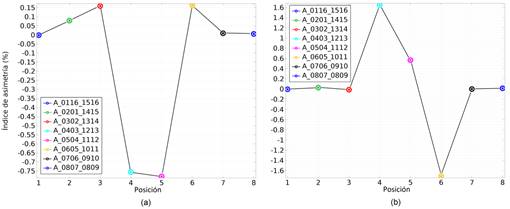
Figura 7 Índices de asimetría hemisférica obtenidos de las simulaciones del potencial eléctrico para el modelo de cabeza humana de un sujeto con: (a) - una lesión cerebrovascular isquémica de tamaño 1 con una conductividad eléctrica de 0.13 S/m, localizada en la región temporal; (b) - una lesión cerebrovascular hemorrágica de tamaño 1, localizada en la región temporal frente al electrodo 4, adyacente a una lesión cerebrovascular isquémica de tamaño 1 con una conductividad eléctrica de 0.07 S/m, localizada en la región temporal-frontal frente a los electrodos 5 y 6.
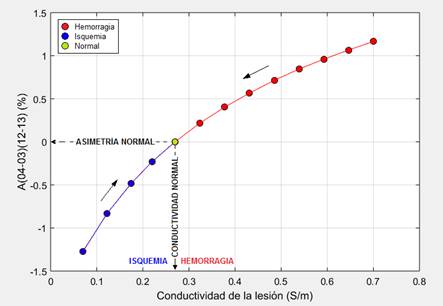
Figura 8 Índice de asimetría contra conductividad eléctrica de la región dañada para una lesión cerebral temporal de tamaño 1.
En este trabajo se simuló el proceso de rehabilitación variando gradualmente la conductividad de la región dañada. En la Fig. 8 se muestra el índice de asimetría A(04(03)(12(13) contra la conductividad eléctrica de la región dañada para una lesión cerebral temporal de tamaño 1. La parte izquierda de la curva (en azul) muestra la tendencia que se espera ver durante el proceso de rehabilitación en el caso de un daño cerebral isquémico, mientras que la parte derecha de la curva (en rojo) muestra la tendencia que se espera ver durante el proceso de rehabilitación en el caso de un daño cerebral hemorrágico. En el caso de una cabeza con una asimetría eléctrica nativa las curvas como la mostrada en la Fig. 8 estarían desplazadas hacia arriba o hacia abajo con relación al origen de coordenadas en dependencia del signo y el valor de la asimetría inicial, como se infiere de los resultados mostrados en [21].
Las tendencias observadas durante el experimento en el índice de asimetría en el entorno de la lesión (positivo o negativo y/o aumentando o disminuyendo) pudieran ser uno de los intereses principales para el monitoreo de las ECV durante el proceso de rehabilitación.
La relación obtenida en este estudio entre el tipo de daño cerebral y el índice de asimetría se puede expresar de forma resumida como se muestra en la Fig. 9, donde Z representa la impedancia,
4.- Discusión
En este trabajo se analiza la viabilidad de usar los marcos de medición de la EIT en una manera más directa, sin el paso de reconstrucción de la imagen, matemáticamente dificultoso y desafiante. En escenarios que no requieren de una imagen inmediata, tales como la clasificación de la ECV, puede ser suficiente admitir o descartar definitivamente una hemorragia. La información relacionada con la presencia o la ausencia de una perturbación como esa en la región de interés está codificada en el marco de medición de la EIT, por tanto, está en los índices de asimetría definidos. La base para esto es el conocimiento a priori de que existe una diferencia notable en la conductividad entre el tejido dañado y el normal.
El modelo computacional usado fue un modelo FEM hemisférico de la cabeza y el cerebro humanos. La cabeza es una estructura anatómicamente compleja, pero para los propósitos de la EIT, y por tanto también de la EBI, se pueden hacer simplificaciones enfocándose en los tejidos que tienen un efecto significativo sobre la conducción de la corriente eléctrica. Típicamente las simulaciones de EIT usan un modelo de cuatro capas, como aquí, el cual incluye al cerebro como la capa más interna, a la capa de fluido cerebroespinal eléctricamente conductiva, inmediatamente externa a este, al altamente resistivo cráneo, y al moderadamente resistivo cuero cabelludo [33]. Un modelo computacional simplificado como este facilita el desarrollo de un modelo físico equivalente, lo cual está fuera del alcance de este trabajo, permitiendo la comparación entre los resultados computacionales y los resultados del modelo físico. Además, el modelo usado fue “computacionalmente ligero”, lo que permitió el desarrollo rápido de varios modelos de prueba. Naturalmente, existen modelos más complejos, los cuales pueden ser relevantes en dependencia de lo que se investiga. Por ejemplo, en la literatura se han reportado modelos físicos de cabeza que modelan las diferencias de conductividad a través del cráneo [35, 36].
Bagshaw y col. [25] presentaron un algoritmo de reconstrucción de imágenes validado para la EIT de la función del cerebro humano, el cual usa el método de los elementos finitos para incorporar geometría y conductividades realistas en el modelo directo. La intención del trabajo fue responder tres cuestiones: (1)- ¿cuál es la ventaja de usar una geometría realista de la cabeza, (2)- ¿cuál es la ventaja de usar una geometría de la cabeza formada por cascarones esféricos de diferentes conductividades?, (3)- ¿Cuánta diferencia provoca lo anterior en las imágenes reconstruidas a partir de datos recopilados en voluntarios humanos? Concluyeron que el uso de una geometría realista en el problema directo conduce a una ligera mejoría en la calidad de la imagen y en la exactitud de la localización, siendo la mejoría en la calidad de la imagen más significativa que los efectos en la exactitud de la localización o en la resolución. Del análisis de los datos de los experimentos con voluntarios humanos sugirieron que los beneficios más significativos de usar un modelo directo más exacto serían evidentes al intentar obtener imágenes funcionales del cerebro humano. Por consiguiente, se puede esperar que los resultados presentados aquí, basados en los valores de los índices de asimetría definidos y no en la imagen de la lesión, no sean afectados significativamente por el uso de un modelo de cabeza hemisférico formado por cuatro capas de conductividad.
En las simulaciones de EIT típicamente las lesiones cerebrovasculares son modeladas como esferas, cubos, o cilindros dentro de la capa del cerebro [15, 19, 20, 21, 22, 25, 28, 29, 30, 31, 32, 33], lo cual es una simplificación; las hemorragias intracerebrales, por ejemplo, pueden ser más elipsoidales [30]. En [22], Towers y col. modelaron las lesiones en el modelo numérico como cubos. En [31], McDermott y col. modelaron las lesiones en el modelo numérico como esferas, mientras que en el modelo físico las modelaron como cubos de un volumen equivalente, localizados en las mismas posiciones, lo que hicieron con el objetivo de validar experimentalmente la técnica. En [28], Jieshi Ma y col. modelaron las lesiones como discos en el modelo numérico 2D, mientras que en el modelo físico las modelaron como cilindros con el área de la base igual al área de los discos del modelo numérico. Por consiguiente, se puede inferir que al nivel actual de desarrollo de la EIT y de la EBI, al modelar las lesiones cerebrovasculares como objetos de diferente forma, como las mencionadas anteriormente, se pueden esperar resultados similares influenciados solo por el volumen de la lesión, independientemente de su forma.
Un amplio espectro de lesiones es posible en la ECV. En Fiebach y col., por ejemplo, el volumen hemorrágico en la ECV aguda fue reportado en el rango desde 1 cm3 hasta 101.5 cm3, donde un volumen mediano de 10 cm3 y medio de 17 cm3 es típico [37], mientras que Payabvash y col. reportaron una lesión isquémica promedio de 39.5 ± 84.9 cm3[38]. En pacientes con ECV una hemorragia de 30 cm3 es un tamaño umbral asociado con malos desenlaces, mientras que 60 cm3 es un umbral para una mortalidad significativa [33]. Por eso, y teniendo en cuenta además que el problema de la sensibilidad del potencial eléctrico con respecto a pequeñas perturbaciones de amplitud en la conductividad (caso de lesiones pequeñas y profundas) ha sido bastante estudiado y está fuera del alcance de este trabajo, se han seleccionado aquí volúmenes de 8 cm3 y de 64 cm3 como representativos de lesiones pequeñas y grandes, localizadas en las cercanías de la superficie del cerebro.
Por ejemplo, Boverman y col. [39] evaluaron la posibilidad de un sistema físico de EIT con 32 electrodos de Ag/AgCl de detectar una microhemorragia en las cercanías del centro de la cabeza. Para ello simularon las corrientes usadas típicamente por el sistema y le agregaron a las partes real e imaginaria de los potenciales medidos un gran número de componentes de ruido Gaussiano independientes, generadas aleatoriamente, distribuidas idénticamente, con varianzas derivadas de experimentos usando cargas resistivo-capacitivas constantes en el tiempo conocidas. Además del ruido aleatorio simularon también una variación sistemática de las impedancias de contacto electrodo-piel con propiedades estadísticas derivadas del estudio en un sujeto humano. La idea era que si se pueden estimar las variaciones en el tiempo de tales impedancias, también se pueden compensar estas. Dado el conocimiento de las propiedades eléctricas, de la geometría del cerebro, de las corrientes aplicadas y de las varianzas del ruido, fueron capaces de generar una simulación de Monte Carlo detallada del desempeño del sistema en la detección de una microhemorragia de volumen y posición conocidos, mostrando la posibilidad potencial de la EIT de detectar microhemorragias superficiales y profundas con un volumen de hasta 5 cm3
Una técnica de monitoreo ideal tendría que penetrar las capas protectoras que rodean al tejido cerebral incluyendo el pelo, el cuero cabelludo, el cráneo y el fluido cerebroespinal, aunque preservando el subyacente tejido cerebral a estudiar. Para el monitoreo funcional sería deseable un rango de resoluciones temporales para diferenciar entre la actividad neuronal, en la escala de tiempo de los subsegundos, y el flujo sanguíneo cerebral, en la escala de tiempo de los suprasegundos. Por supuesto que también serían deseables una alta sensibilidad para detectar lesiones profundas y una alta resolución espacial.
Existe una larga lista de técnicas que actualmente están en uso en las clínicas o bajo investigación para el monitoreo y la obtención de imágenes de la función cerebral en las escalas de tiempo desde los subsegundos hasta los suprasegundos. Estas incluyen la IRMf, la SPECT, el ultrasonido, la EEG, la Magnetoencefalografía (MEG), la Tomografía Óptica Difusa (DOT) de la Espectroscopia del Infrarrojo Cercano funcional (fNIRS), la Señal Óptica Relacionada con Eventos (EROS) y la EIT. En la Tabla 2 se muestran para su comparación algunas de las características más relevantes de tales técnicas [40, 41, 42]. Comparada con las otras técnicas, la EIT tiene la ventaja de su alta resolución temporal, portabilidad, no invasividad y bajo costo (incluyendo los costos de operación), costo que se reduciría aún más si esta es usada para el monitoreo sin el paso de reconstrucción de la imagen (EBI en lugar de EIT). Por otro lado, la principal desventaja de la EIT es su relativa baja resolución espacial y su baja sensibilidad de profundidad en comparación con técnicas como la fMRI y la SPECT.
Típicamente los sistemas de EIT usan arreglos de 8, 16, 32 o 64 electrodos en un anillo o anillos y los varios cientos de mediciones de impedancia a partir de diferentes combinaciones de electrodos, necesarios para producir una única imagen, son recolectados y reconstruidos varias veces por segundo [33, 41, 42, 43, 44]. La configuración de los electrodos, su número, el protocolo de medición, la magnitud de la corriente y la frecuencia son dependientes de la aplicación particular [33]. El uso del método de cuatro electrodos para medir la impedancia, en el cual una corriente constante es aplicada a dos electrodos y la diferencia de potencial resultante es registrada en los otros dos minimiza el error debido a la impedancia de contacto electrodo-piel. La selección de un arreglo anular de 16 electrodos en este trabajo se ha hecho meramente con el objetivo de ilustrar la aplicación de los índices de asimetría propuestos para la clasificación y el monitoreo de la lesión cerebrovascular.
Al considerar las características eléctricas del contacto del electrodo con la piel, además de la impedancia de contacto electrodo-piel se debe tener en cuenta la impedancia de contacto de la superficie de los electrodos, la cual caracteriza al material de los electrodos y permite una vía externa para la corriente que normalmente circularía dentro del cuerpo [45]. Esta impedancia puede ser reducida eficientemente por la geometría de los electrodos o por su separación [46]. La sensibilidad y la resolución del sistema de EIT se pueden aumentar usando un arreglo de electrodos más denso, pero hasta cierto límite, ya que al disminuir la distancia entre los electrodos de medición entraría menos corriente en el cerebro debido al efecto de la impedancia de contacto de la superficie de los electrodos, y por consiguiente disminuiría la sensibilidad.
Tabla 2 Características relevantes de las técnicas de imágenes funcionales [40-42]
| Técnica de imagen funcional | Características | |||
|---|---|---|---|---|
| Resolución espacial | Resolución temporal | Sensibilidad de profundidad | Portabilidad | |
| fMRI | Hasta 0.1-1.5 mm | 100 ms en el mejor caso; típicamente unos 2 s | - | No |
| SPECT | Hasta 1 mm | Por encima de 1 s | - | No |
| Ultrasonido | Hasta 2 cm | Por encima de 1 s | Hasta 16 cm | Sí |
| DOT/fNIRS | 1-2 cm | En el orden de 10 ms | Hasta 1-2 cm | Sí |
| EROS | Hasta 1-5 mm | Desde 1 ms hasta 100 ms | Hasta 3-5 cm | Sí |
| EEG | Hasta 1-2 cm | Desde 1 ms hasta 100 ms | Hasta 4-5 cm | Sí |
| MEG | Hasta 3 mm | Desde 4 ms hasta 100 ms | Hasta 1-2 cm | No |
| EIT | Hasta 7-8 mm | Hasta 2 ms | Hasta 5-6 cm | Sí |
En las simulaciones numéricas de EIT típicamente se usan electrodos de cobre con un diámetro de alrededor de 10 mm [30], de forma circular o cuadrada y se desprecia la impedancia de contacto electrodo-piel [19, 20, 21, 22, 25, 28, 29, 30, 31, 32, 33], como aquí, o se le asigna a esta un valor constante en el tiempo, como en [15], a menos que se persiga investigar la sensibilidad del potencial eléctrico con respecto a pequeñas perturbaciones de amplitud en la conductividad, como en [39] o en [46], donde se usó el denominado Modelo de Electrodos Completo (CEM), el cual incorpora con precisión en el problema directo de la EIT el tamaño de los electrodos, la forma de estos y la impedancia de contacto efectiva.
A la temperatura de 36 ℃, la razón de la conductividad de la plata a la del cobre es tan cercana a la unidad (≈1.06) que, al sustituir un material por el otro en las simulaciones numéricas de EIT, el efecto sobre la distribución de la corriente dentro de la cabeza es prácticamente despreciable, y como las propiedades eléctricas del cobre casi siempre se tienen a mano, esto puede explicar por qué típicamente en las simulaciones se usan electrodos de cobre en lugar de electrodos de plata.
Para facilitar su aplicación, los electrodos reales de EIT son a veces incorporados en un cinturón o arnés, pero también son aplicados directamente. Típicamente se usan electrodos no polarizables de Ag/AgCl, del tipo ECG [42]. La impedancia de contacto electrodo-piel crea una acumulación de cargas cuando el electrodo porta corriente, lo que resulta en una polarización del electrodo y en potenciales de polarización que disminuyen con la distancia. Usando electrodos no portadores de corriente como pares de medición, se reduce la contribución de los potenciales de polarización a las mediciones del potencial [42]. Cuando se estimula a frecuencias en el rango de los kHz, como lo hacen la mayoría de los sistemas, la polarización de los electrodos es un efecto menos significante [45].
Las lesiones cerebrovasculares unilaterales a menudo generan síntomas en otras partes del cuerpo [47], lo que pudiera utilizarse para determinar cuál es el hemisferio cerebral dañado. Se han propuesto también mediciones efectivas de EBI cerebral para determinar cuál fue el hemisferio dañado por una lesión cerebrovascular unilateral [48]. De esta manera, en este trabajo se presupone que se conoce a priori cuál es el hemisferio dañado. Otros autores han procedido de la misma manera, por ejemplo Cohen y col. en [21] y Jieshi Ma y col. en [28].
Las simulaciones numéricas de este trabajo demostraron que el índice de asimetría definido fue sensible en el 100 % de los casos considerados para determinar el tipo de lesión y la localización aproximada de la misma, tomando como referencia el hemisferio sano. Además, en el caso de las lesiones de tamaño 1 se obtuvo mayor sensibilidad en las regiones frontal y occipital (aproximadamente 1.2 veces), mientras que en el caso de las lesiones de tamaño 2, con un volumen 8 veces mayor, se alcanzó mayor sensibilidad en la región temporal (también aproximadamente 1.2 veces), tanto para las lesiones isquémicas como para las hemorrágicas.
Al evaluar la sensibilidad para lesiones de diferente tamaño localizadas en una misma región, el mayor valor se obtuvo para lesiones temporales (aproximadamente 4 veces al multiplicar el volumen de la lesión por 8). Usando un modelo numérico de cabeza humana más realista, Cohen y col. en [21] reportaron también un aumento del índice de asimetría hemisférica definido por ellos, al aumentar el volumen de la lesión, el cual fue de aproximadamente entre 1.05 y 4 veces, según el tipo de lesión y su localización al multiplicar el volumen por 8.
Para ambos tipos de lesión, hemorrágica e isquémica, los resultados mostraron que en el caso de lesiones frontales y temporales el índice de asimetría alcanzó su valor máximo en las cercanías del electrodo más cercano a la lesión, mientras que en el caso de lesiones occipitales el índice de asimetría alcanzó su valor máximo en las cercanías del electrodo adyacente a la lesión que se encuentra más alejado del sumidero de corriente, es decir, del electrodo 0(16). En la Fig. 10 se muestran los resultados de un estudio más detallado de la dependencia de la posición correspondiente al valor máximo del índice de asimetría con la posición de la lesión, para lo cual se consideraron 15 posiciones de una lesión de tamaño 1 comprendidas entre el electrodo 0(16) y el electrodo 8, con un desplazamiento angular de 11.25 º, localizadas espacialmente a la misma distancia radial que las lesiones de tamaño 1 mostradas en la Fig. 2. El espacio comprendido entre los electrodos 0(16) y 8 se dividió en tres partes que representan convencionalmente las regiones frontal, temporal y occipital.
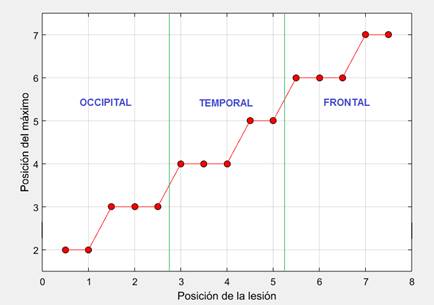
Figura 10 Posición correspondiente al máximo del índice de asimetría contra posición de una lesión de tamaño 1.
Como se puede ver, en el caso de una lesión en la región occipital, el máximo valor del índice de asimetría se correspondió con la posición 2 para lesiones en las posiciones 0.5 y 1, mientras que se correspondió con la posición 3 para lesiones en las posiciones 1.5, 2 y 2.5. En el caso de una lesión en la región temporal, el máximo valor del índice de asimetría se correspondió con la posición 4 para lesiones en las posiciones 3, 3.5 y 4, mientras que se correspondió con la posición 5 para lesiones en las posiciones 4.5 y 5. Finalmente, en el caso de una lesión en la región frontal, el máximo valor del índice de asimetría se correspondió con la posición 6 para lesiones en las posiciones 5.5, 6 y 6.5, mientras que se correspondió con la posición 7 para lesiones en las posiciones 7 y 7.5. Así, si el máximo del índice de asimetría se corresponde, por ejemplo, con la posición 3, esto significa que la lesión puede encontrarse en cualquier lugar entre las posiciones 1.5 y 2.5 de los electrodos. Para el caso de lesiones de tamaño 2 se obtuvieron resultados similares. Por tanto, en todos los casos el biomarcador desarrollado permitió localizar aproximadamente la región dañada dentro del hemisferio dañado.
En este trabajo se encontraron niveles altos de asimetría eléctrica en el hemisferio que contenía la lesión con relación al hemisferio sano. Esto se debe a que la conductividad de una lesión hemorrágica sin tratamiento (típicamente unos 0.7 S/m) es más alta que la del tejido cerebral circundante y la del hemisferio contrario (0.27 S/m), mientras que la conductividad de una lesión isquémica sin tratamiento (típicamente entre unos 0.13 S/m y 0.07 S/m, dependiendo del tiempo transcurrido desde el inicio del ictus) es más baja que la del tejido cerebral circundante y la del hemisferio contrario, lo que ha sido reportado por otros autores [21, 22, 26, 28, 29, 30, 31, 32, 33, 49].
De la ecuación 5 para el índice de asimetría hemisférica A RL se infiere que, en el caso de una lesión isquémica localizada en el hemisferio derecho, la diferencia de potencial φ m ( φ n de la pareja de electrodos del hemisferio derecho relacionada con la posición de la lesión, es mayor que la diferencia de potencial φ p ( φ q de la pareja de electrodos contraparte en el hemisferio izquierdo, por esto el índice de asimetría correspondiente a la posición de una lesión isquémica es negativo.
Por el contrario, en el caso de una lesión hemorrágica localizada en el hemisferio derecho, la diferencia de potencial φ m ( φ n de la pareja de electrodos del hemisferio derecho relacionada con la posición de la lesión, es menor que la diferencia de potencial φ p ( φ q de la pareja de electrodos contraparte en el hemisferio izquierdo, por esto el índice de asimetría correspondiente a la posición de una lesión hemorrágica es positivo.
Las investigaciones desarrolladas sobre las ECV han definido dos fases fundamentales teniendo en cuenta la progresión del daño cerebral. La primera es la fase aguda, donde se debe realizar un diagnóstico diferencial rápido y oportuno para mejorar el pronóstico de supervivencia y evitar la morbilidad, y una segunda fase, relacionada con la rehabilitación, la cual generalmente, abarca un largo periodo de tiempo, en la cual se producen cambios en las propiedades dieléctricas de la lesión [21, 50, 51] en su evolución hacia el estado normal.
La fase aguda comprende las primeras horas de transcurrida la enfermedad. En ella no se tiene el conocimiento a priori de la asimetría eléctrica hemisférica del tejido cerebral sano del paciente, ni se conoce cuál es el hemisferio cerebral afectado. En la mayoría de los casos las lesiones producidas son locales [9], aunque puede ser una ECV generalizada con lesiones en ambos hemisferios. En cualquier caso, será necesario emplear otras técnicas y métodos, incluyendo las variables obtenidas en el examen clínico del paciente, o aplicar un procedimiento de EBI como el propuesto por Atefi y col. en [48] para determinar cuál es el hemisferio sano, y así poder usar este como referencia.
En la segunda fase, durante el periodo de rehabilitación, se producen cambios significativos en la magnitud y tendencia del índice de asimetría debido a la evolución de la lesión, como se muestra en la Fig. 8. Además se tiene mucha más información relacionada con la ECV, incluidos los estudios por medio de imágenes médicas los cuales pueden ser utilizados como “Gold Standard” para determinar la localización exacta de la lesión. En esta fase se presentan otros retos asociados con el monitoreo, y es el caso del edema cerebral secundario a la hemorragia, lo cual es una complicación frecuente en la variante hemorrágica de esta enfermedad. El edema cerebral afecta de forma evidente al tejido cerebral sano circundante y este a su vez afecta la magnitud de la asimetría eléctrica. En la actualidad se trabaja en posibles maneras para abordar esta problemática, empleando los parámetros bioeléctricos que pueden ser obtenidos a través de EBI, los cuales son sensibles a los cambios en la distribución de líquido en los tejidos [52, 53].
En esta investigación se asumió que en el caso de la variante hemorrágica de ECV la conductividad del tejido dañado (σ = 0.7 S/m) es mucho mayor que la del tejido cerebral sano (σ = 0.27 S/m) debido al incremento en la cantidad de sangre en el espacio subdural o subcranoideo, mientras que en el caso de la variante isquémica de la enfermedad la conductividad eléctrica del tejido dañado (σ = 0.07(0.13 S/m) es mucho menor que la del tejido cerebral sano debido a la coagulación de la sangre. Resultados obtenidos en investigaciones previas soportan estas suposiciones [15, 17, 20. 21].
Los resultados obtenidos son coherentes con los reportados por otros investigadores en estudios experimentales y teóricos a partir de simulaciones numéricas. En tal sentido, se destacan los resultados experimentales preliminares obtenidos por Seoane y col. en [54] en 4 pacientes con lesión hemorrágica y 6 con lesión isquémica, los cuales mostraron que las mediciones de bioimpedancia eléctrica en los hemisferios derecho e izquierdo son significativamente diferentes en los casos agudos de ictus unilateral dentro de las primeras 24 horas de transcurrido el ataque. Las hemorragias estaban localizadas centralmente en dos pacientes (una en el putamen derecho y una en el lóbulo occipital medio derecho) y lateralmente en los otros dos (una en el opérculo izquierdo y una en la parte lateral del lóbulo occipital derecho). Las seis lesiones isquémicas eran de varios tamaños y localizaciones. Tres eran lesiones grandes en el territorio alimentado por la arteria posterior izquierda. Dos eran infartos en la región alimentada por la arteria media derecha. Un paciente tenía infartos pequeños en el núcleo caudado izquierdo y en el putamen, no visibles en el escaneo inicial de TC.
Se destacan también los resultados obtenidos por Atefi y col. en [20] a partir de simulaciones numéricas de los potenciales eléctricos en modelos de cabeza humana 3D realistas y a partir de experimentos en humanos (10 sanos y 6 con hemorragias intracraneales de volumen entre 6 y 53 cm3), quienes reportaron que la diferencia entre las diferencias de potencial izquierda-derecha de los pacientes con hemorragia intracraneal y los controles sanos fue estadísticamente significativa con un nivel de significancia de un 5% usando una prueba t de Welch de dos muestras. En el caso de las simulaciones, la diferencia de potencial entre los modelos dañado y sano fue cero dondequiera sobre la superficie de la cabeza, excepto en la vecindad de la lesión, donde esta varió hasta un 5% para una hemorragia intracraneal esférica de 25.3 cm3, localizada en el lóbulo frontal izquierdo del cerebro, cerca de la superficie de la cabeza. La comparación de estos resultados y los obtenidos por Cohen y col. en [21] con los obtenidos en este trabajo demuestra que se puede llegar a conclusiones similares usando un modelo numérico de cabeza mucho más sencillo.
Los resultados presentados aquí forman parte de una investigación en curso, por lo que están basados en suposiciones iniciales. Al aplicar la técnica de bioimpedancia en la cabeza, existen varios factores que afectan el flujo de la corriente inyectada. Las conductividades del cuero cabelludo (σ = 0.19 S/m) y del fluido cerebroespinal (σ = 1.79 S/m) son mayores que la conductividad del cráneo (σ = 0.018 S/m), el cual se encuentra entre esas dos capas, por lo que se crea un efecto de derivación o shunt. Este efecto es amplificado por la naturaleza anisótropa de los tejidos del cuero cabelludo y del cráneo, y hace más difícil identificar los cambios en las propiedades eléctricas de dichos tejidos.
Varios estudios han investigado el porcentaje de corriente aplicada que entra en el cerebro, mostrando que en promedio es un 15% en el caso de conejos anestesiados [55] y un 36% en el caso de cerdos vivos [56]. En humanos un estudio realizó mediciones en un modelo de cabeza físico realista con y sin el cráneo [57] y mostró que las variaciones de impedancia dentro del cerebro eran atenuadas en un factor de 8.2, 5.5 y 5.6 para los compartimientos coronales anterior, central y posterior (12.2%, 18.2% y 17.9% de penetración), respectivamente. En resumen, el cráneo es la razón por la cual la EIT y la EBI del cerebro son tan difíciles. A pesar de eso, la impedancia medida sobre el cuero cabelludo es influenciada por la distribución de la conductividad en el cerebro y por la redistribución de los espacios ocupados por la sangre y el fluido cerebroespinal en la cavidad craneal [45]. Otros factores fisiológicos, tales como la actividad de las neuronas en el cerebro, pueden afectar también la impedancia medida, lo que se debe a la sensibilidad de las técnicas de bioimpedancia cerebral a las variaciones de la conductividad en el objeto de medición.
La actividad funcional del cerebro, que tiene lugar en la escala de tiempo de los suprasegundos, es generalmente de una naturaleza fisiológica, por ejemplo, variaciones en el flujo/volumen sanguíneo, hinchazón de las células, o la actividad metabólica, y es denominada respuesta hemodinámica [58]. Esta actividad ocurre típicamente 5 s después que se aplica un estímulo nervioso y provoca cambios relativamente grandes en la impedancia cerebral, es decir, desde el orden del 1 % hasta el orden del 10 % [59, 60], siendo este el caso de las lesiones cerebrovasculares.
La actividad neuronal es debida a la señalización de las neuronas y a las transmisiones sinápticas asociadas (eléctrica y química). La transmisión sináptica química más rápida tiene lugar durante aproximadamente 1-5 ms, y es más lenta que la transmisión sináptica eléctrica, que dura alrededor de una fracción de ms, al nivel de una sola sinapsis [61]. La señalización neuronal total en respuesta a un estímulo dado es la transmisión a través de billones de fisuras sinápticas presentes en el cerebro y su efecto acumulado es una respuesta evocada, la cual es desarrollada durante unas pocas decenas de ms. En los humanos toma 50 ms transmitir la información desde la retina hasta la corteza visual cerebral, mientras que la conciencia del estímulo se desarrolla 500 ms después que este se inicia en la corteza [62]. Por otro lado, un solo pulso suministrado a la piel puede evocar un impulso potencial en la corteza cerebral en 20 ms [62]. Para la investigación de la conciencia se ha sugerido como significante una duración mínima de tiempo de 250 ms [63]. La actividad neuronal provoca cambios relativamente pequeños en la impedancia cerebral [40] y como además tiene lugar en una escala de tiempo mucho menor que la de la respuesta hemodinámica, es posible descartar sus efectos al estudiar esta última.
En [64], Murrieta-Lee y col. usaron un sistema de EIT a 9.6 kHz con un anillo de 16 electrodos para monitorear en sujetos humanos áreas del cerebro activadas en respuesta a la presentación de estímulos sensorios. Las imágenes reconstruidas producidas por este experimento mostraron cambios en la conductividad relacionados con áreas de la corteza visual en respuesta a la estimulación visual repetitiva. Los autores concluyeron que los rápidos cambios observados en la conductividad fueron debidos a cambios funcionales que ocurrieron en la juntura sináptica de las neuronas visuales dentro de la corteza visual, demostrando la capacidad de la EIT para monitorear la actividad funcional dentro del cerebro en la escala de tiempo de los subsegundos, debida a la actividad sináptica.
Uno de los retos importantes a resolver por la EIT y por la EBI, es lograr que los electrodos no se corran respecto a sus posiciones ideales y hagan un contacto aceptable con una baja capacidad C C con el cuero cabelludo en presencia de un cabello espeso. Los electrodos estándar de ECG no son apropiados para el uso sobre el cabello debido a que ellos se ponen sobre la cima en lugar de penetrar a través del pelo. Estudios usando electrodos de ECG han tenido que afeitar la cabeza de los participantes para obtener una buena calidad de señal [65], por lo que no son prácticos. Por tanto, el desarrollo de un arreglo de electrodos que logre un contacto adecuado en presencia de un cabello espeso aumentaría grandemente la accesibilidad de la EIT y de la EBI. Un arreglo de electrodos para EIT o EBI debe ser rápido de montar, ser confortable, tener electrodos con una baja capacidad de contacto, ser robusto ante el movimiento y el ruido, y ser fácil de limpiar y/o esterilizar entre usos.
En [66], Avery desarrolló un casco con electrodos de acero inoxidable 316 de 10 mm de diámetro, controlado por servomotores. Este caso reduce C C mediante el desgaste del cuero cabelludo a través de la acción de servomotores que también sirven para mantener constante la presión de los electrodos contra el cuero cabelludo. El autor encontró que la mayor reducción en C C se logró después de una rotación de cada electrodo contra el cuero cabelludo. En [67], Liu y col. desarrollaron un arreglo de electrodos de BeCu de contacto por muelle recubiertos con nanopartículas de Pt, logrando una reducción significativa de C C a frecuencias por debajo de 100 Hz. A la frecuencia de 10 kHz, los electrodos alcanzaron una impedancia de contacto de cerca de 225 (, contra los 300 ( obtenida usando los electrodos estándar de Ag/AgCl. Estos resultados sugieren que el recubrimiento de los electrodos de Ag/AgCl con nanopartículas de Pt pudiera reducir mucho más su impedancia de contacto con la piel.
Se debe señalar que, para aplicar en la práctica el método presentado aquí, se debe garantizar la distribución simétrica de los electrodos a ambos lados de la cabeza, ya que la distribución asimétrica de los mismos puede conducir a la detección de una asimetría no nativa no relacionada con la lesión cerebrovascular. Esto no fue un problema en el presente estudio, ya que, en el modelo numérico, los electrodos fueron posicionados simétricamente con relación al plano sagital medio. Para garantizar la distribución simétrica de los electrodos sobre la cabeza, se debe medir con precisión la posición de cada electrodo en los sujetos humanos antes de colocarlos en la posición correcta [28]. Algunos autores han empleado el sistema digitalizador Polhemus FASTRAK para posicionar los electrodos con precisión [68].
Otro reto a resolver por la EIT y la EBI son las interferencias del movimiento de la cabeza, las cuales se originan principalmente a partir del movimiento del cuerpo de los pacientes y de los procedimientos de enfermería realizados por el personal médico. Tales movimientos conducirán a variaciones en los potenciales eléctricos medidos, lo que afectará a la reconstrucción de la imagen, en el caso de la EIT, y a los índices de asimetría determinados, en el caso del método de EBI presentado aquí. En Zhang y col. emplearon un método de preprocesamiento de datos basado en la descomposición wavelet con el objetivo de inhibir las interferencias del movimiento de la cabeza en los datos de impedancia. El sistema usado requería de la fijación de un arreglo anular de 16 electrodos en la cabeza de los sujetos. Adoptaron el protocolo de excitación opuesta y excitación adyacente. Los experimentos en dos humanos demostraron que el método suprimió efectivamente el movimiento de la cabeza en las señales, reduciendo así los artefactos correspondientes en las imágenes obtenidas. Este método es prometedor, por lo que debería probarse en un mayor número de sujetos.
Los índices de asimetría hemisférica definidos en esta investigación son más generales que el índice de asimetría hemisférica AI usado por Cohen y col. en [21], asociado a los electrodos de EEG del sistema internacional 10-20, ya que en ese caso los potenciales φ n y φ q en las ecuaciones (5) y (6) tienen un valor fijo igual al potencial del electrodo central Cz. Esto le otorga relevancia al biomarcador desarrollado aquí, el cual no está asociado a ningún arreglo de electrodos particular y, a diferencia del biomarcador usado en [21], permite localizar aproximadamente la región dañada dentro del hemisferio dañado sin la necesidad de que sean conocidos a priori los valores iniciales (normales) del biomarcador para cada posición explorada, permitiendo así un monitoreo de la lesión más confiable.
Como se dijo más arriba, el método de EBI cerebral presentado aquí presupone que se conoce a priori que la lesión cerebrovascular a clasificar y/o monitorear es unilateral y que se sabe cuál es el hemisferio cerebral dañado, lo que pudiera determinarse a partir de los síntomas generados en otras partes del cuerpo del paciente, o a partir de mediciones de bioimpedancia eléctrica como las propuestas en [48]. De ser eso así, el método presentado tendría la ventaja de no necesitar de las técnicas imagenológicas estándares para obtener esa información preliminar. Sin embargo, incluso si fuera necesario recurrir a tales técnicas para obtener dicha información, lo cual de paso permitiría clasificar la ECV a partir de las imágenes obtenidas, se tendría aun la ventaja de contar con una técnica apropiada para las aplicaciones de monitoreo prolongado debido a su seguridad, su alta resolución temporal, pequeño tamaño y bajo costo. Los resultados obtenidos en este trabajo evidencian la posibilidad de desarrollar un nuevo método complementario para el diagnóstico diferencial y el monitoreo de la ECV basado en la técnica de bioimpedancia eléctrica cerebral.
5.- Conclusiones y trabajo futuro
En el presente trabajo se analizaron las potencialidades y la viabilidad de la técnica de bioimpedancia cerebral como método complementario para el diagnóstico diferencial de la ECV mediante modelación numérica en un modelo hemisférico de la cabeza humana empleando el método de los elementos finitos. Se desarrolló un biomarcador, basado en índices de asimetría eléctrica, capaz de diferenciar las variantes isquémica y hemorrágica de esta enfermedad. El daño cerebral fue modelado a través de variaciones en la propiedad eléctrica conductividad del tejido cerebral, así como las dimensiones de la lesión.
Los resultados obtenidos a partir de las simulaciones muestran un valor positivo para el índice de asimetría hemisférica en el entorno de una lesión hemorrágica y un valor negativo en el caso de una lesión isquémica, lo cual está relacionado con la mayor conductividad del tejido hemorrágico y la menor conductividad del tejido isquémico en comparación con la conductividad del tejido cerebral normal. El índice de asimetría fue capaz de diferenciar el 100 % de las lesiones isquémicas y hemorrágicas de 8 cm3 y 64 cm3 consideradas, localizadas en las regiones frontal, temporal y occipital.
Para lesiones de tamaño 1, el biomarcador mostró mayor sensibilidad en las regiones frontal y occipital (aproximadamente 1.2 veces), mientras que en el caso de las lesiones de tamaño 2, con un volumen 8 veces mayor, este mostró mayor sensibilidad en la región temporal (también aproximadamente 1.2 veces), tanto para las lesiones isquémicas como para las hemorrágicas. Para lesiones de diferente tamaño localizadas en una misma región, fue mayor para las lesiones en la región temporal (aproximadamente 4 veces al multiplicar el volumen de la lesión por 8).
En un trabajo futuro, el método presentado aquí será investigado usando un modelo numérico de cabeza más realista y diferentes arreglos de electrodos, así como un modelo físico equivalente.