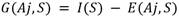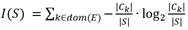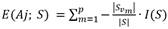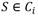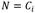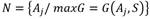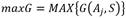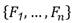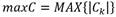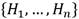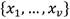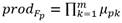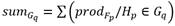Introducción
En los sistemas industriales actuales es una necesidad aumentar la productividad, la eficiencia, la calidad de los productos y satisfacer, las cada vez más rigurosas, regulaciones de seguridad y medioambientales. Para contribuir con esos propósitos a los sistemas industriales le son incorporadas capacidades de monitoreo de sus estados que permiten el desarrollo de sistemas de diagnóstico de fallos. Estos sistemas tienen como objetivo detectar, identificar y localizar de manera temprana los fallos que se produzcan para tratar de evitar un comportamiento no adecuado del proceso [1].
A pesar de los grandes avances en la tecnología, el diagnóstico de fallos sigue constituyendo un reto; razón por la cual actualmente sigue siendo un tema ampliamente investigado [2, 3, 4, 5, 6, 7]. Las técnicas para el diagnóstico de fallos se pueden dividir en dos grandes grupos: basadas en modelos y basadas en datos [7,8]. No obstante, en algunos trabajos, como por ejemplo [9], también mencionan el enfoque del análisis de señales como otro grupo. Hay que destacar que los métodos basados en modelos y análisis de señales tienen entre sus desventajas que requieren del conocimiento previo de las respuestas del sistema ante los fallos, así como la obtención de un modelo preciso del proceso. Además, generalmente estos se diseñan para un sistema en específico, lo que dificulta realizar modificaciones para la incorporación de aquellos fallos que posteriormente se deseen diagnosticar. Sin embargo, el acercamiento basado en datos consiste en aprovechar, con el uso de técnicas estadísticas o las de aprendizaje de máquina, los datos históricos adquiridos de los sistemas bajo estudio. Estos algoritmos extraen de las muestras, la información redundante que se encuentran en las variables, lo que les ha permitido convertirse en la alternativa más adecuada para enfrentarse a procesos de alta complejidad [10].
Los métodos basados en datos permiten el desarrollo de tareas como la clasificación y la regresión [11]. Varias técnicas se han desarrollado para hacerle frente a las tareas de clasificación usando el enfoque de minería de datos: redes neuronales, árboles de decisión, máquinas de soporte de vectores, entre otras. El empleo de árboles de decisión suele ser recomendado para cuando se desea lograr un buen entendimiento del proceso de clasificación [12].
Los árboles de decisión empleados en el diagnóstico de fallo no son lo mismo que los árboles de fallo. El análisis de árboles de fallo es una técnica probabilística en la cual se usan puertas lógicas booleanas para estimar el riesgo de un “evento superior” en el sistema basado en la probabilidad de sus “causas raíces” [13]. Algunos trabajos que demuestran la aplicación de esta técnica son [14, 15, 16, 17]. En este trabajo nos enfocaremos específicamente en los árboles de decisión y el empleo de la lógica difusa aplicados al diagnóstico de fallos.
El análisis a partir de clasificadores basados en árboles de decisión tiene un amplio uso en el diagnóstico de fallos [18]. Entre las principales ventajas de esta técnica destacan la facilidad para su comprensión; velocidades de aprendizaje y clasificación satisfactorias; robustez ante datos discretos, binarios y continuos y robustez en la interpretación de valores faltantes [19]. En [20] se presenta un resumen de los avances obtenidos relacionados a esta técnica, incluyendo desde los algoritmos de inducción y los criterios de división hasta sus combinaciones con otras técnicas de clasificación.
Aunque los árboles de decisión tienen su origen en el siglo pasado todavía siguen demostrando su aplicabilidad, tal y como se demuestra en [21, 22, 23, 24, 25]. Los mismos han demostrado su eficacia en el diagnóstico de fallos de engranajes en sistemas rotatorios a partir del análisis de características de los datos como la desviación estándar, máximo, mínimo y varianza de una señal vibratoria medida con un acelerómetro [26]. Otras investigaciones también han probado la efectividad de la incorporación de la lógica difusa [27, 28, 29]. En [8] se añade a una técnica de diagnóstico no destructivo para las aspas de motores en aeronaves. Aquí, el análisis de componentes principales para la reducción de la dimensionalidad de los datos derivaba en pérdida de información. Pero este problema logró solucionarse con la representación difusa de los datos, lo que demostró un aumento en la precisión de la clasificación del sistema de diagnóstico. En [30] demuestran la efectividad de dos mejoras del algoritmo ID3 en la inducción de árboles de decisión para su aplicación en el diagnóstico de fallos de circuitos analógicos. La primera consiste en la introducción de lo que denominan “índice de validez de grupo en la ganancia de información” como criterio de división. La segunda mejora trata de considerar las tasas de fallas en la construcción del árbol, lo que permite tener en cuenta tanto la capacidad de partición (o división) de cada atributo como la prioridad de aislamiento de las fallas con mayores tasas. Para el diagnóstico de fallos de circuitos analógicos, en [11] presentan los denominados árboles de decisión difusos de Fisher de múltiples valores. En este caso, la teoría difusa se aplica durante la etapa de discretización de las variables monitoreadas. Lo anterior permite resolver el problema de no contar con límites definidos para la discretización, así como el de la desviación que pudiese ocurrir en las variables. En [31] se propone un método para el diagnóstico de fallos en termoeléctricas basado en árboles de decisión por ser la que mejores resultados aportó en cuanto a precisión al ser comparada con otras técnicas como red neuronal, algoritmo bayesiano y máquina de soporte de vectores.
Debido a que los árboles de decisión se ubican dentro de los denominados métodos supervisados estos necesitan el empleo de un conjunto de datos de entrenamiento. Investigaciones como la de [32] van dedicadas a cómo mejorar el conjunto de datos de entrenamiento para obtener un árbol más preciso. Por otra parte, trabajos como el de [33], proponen algoritmos para perfeccionar la etapa de discretización difusa. Sin embargo, todo ello implica un requisito indispensable: contar con una base de datos de entrenamiento íntegra, que además del funcionamiento normal, contenga conjuntos de datos representativos de los fallos que se pretenden diagnosticar. Aunque es cierto que el “Internet de las Cosas” (IoT por sus siglas en inglés) ha potenciado la cuarta revolución industrial como una fuente de datos sin precedentes para su posterior análisis [34], no siempre se puede garantizar la confiabilidad de todo ese volumen de datos. Luego, contar con una base de datos de entrenamiento íntegra, que además del funcionamiento normal, contenga conjuntos de datos representativos de los fallos que se pretenden diagnosticar, no constituye un requisito fácil de cumplir. Además, también debe tenerse la clasificación de cada observación en el estado de operación del proceso que le corresponda, pues esta información es la que el algoritmo procesa para llevar a cabo la tarea de inducción del árbol de decisión. Lo anterior constituye una seria desventaja por las dificultades en obtener una base de datos de entrenamiento adecuada. En la literatura científica se presentan algunos métodos no supervisados, como el de [35], que eliminan la etapa de clasificar. Sin embargo, persiste la dificultad de que, si se desea incorporar un nuevo fallo en el diagnóstico, habrá que esperar a obtener una cantidad suficiente de datos del mismo que permita volver a realizar el procedimiento.
El “Lenguaje de marcado de modelo predictivo” (PMML por sus siglas en inglés) es un lenguaje basado en “Lenguaje de Marcas Extensibles” (XML por sus siglas en inglés) que se ha convertido en el estándar de facto para representar no solo modelos predictivos y descriptivos, sino que también preprocesamiento y post-procesamiento de datos. Además, permite el intercambio de modelos entre diferentes herramientas y ambientes de desarrollo, evadiendo incompatibilidades y problemas de software propietarios. El estándar PMML ha sido utilizado para intercambiar modelos en sistemas ciber-físicos los cuales son una de las tecnologías primarias en la industria 4.0 [36,37].
El objetivo y principal contribución de este trabajo es presentar una metodología que no necesita una base de datos de entrenamiento para la construcción del árbol de decisión difuso, sustituyendo la misma por una tabla de síntomas de fallos construida a partir del criterio de los expertos. Esta tabla conformará el núcleo de conocimiento con el que se llevará a cabo la inducción del árbol de fallos basado en el algoritmo ID3. De esta manera, en caso de que se desee hacer una modificación del diagnosticador, basta con realizar una nueva entrevista a los expertos para que definan las nuevas características del proceso y/o de los fallos que se diagnostican o se quieran empezar a diagnosticar. La otra contribución del trabajo lo constituye el aprovechar también el conocimiento de los expertos para llevar a cabo la etapa de discretización difusa lo que permite contemplar todo el universo de discurso de las variables que los propios expertos determinen como necesarias para el diagnóstico de los fallos. Ha de resaltarse que la incorporación de dicho conocimiento se facilitará gracias al manejo de la incertidumbre con la lógica difusa. En el trabajo se presenta también un esquema general de desarrollo de modelos de diagnóstico que utiliza el lenguaje PMML para el intercambio de modelos de inteligencia artificial. El mismo les da soporte a los árboles de decisión entre dos aplicaciones informáticas con las tareas de configuración y monitoreo en línea de procesos respectivamente.
El resto del trabajo está organizado de la siguiente manera, en la sección 2 se presentan los fundamentos teóricos que soportan la presente investigación. En la sección 3 se presenta y analiza la metodología propuesta para el diseño del sistema de diagnóstico de fallos. La aplicación de la metodología propuesta a una planta de tratamiento de agua de la industria biofarmacéutica y la discusión de los resultados obtenidos se desarrolla en la sección 4. Finalmente se presentan las conclusiones y recomendaciones para trabajos futuros.
Materiales y métodos
Discretización difusa de las variables
La lógica difusa se basa en la descripción del universo de discurso de cada variable a partir de la definición de conjuntos difusos. Estos conjuntos estarán representados por una función de pertenencia µ que puede ser de diferentes tipos: triangular, trapezoidal, gaussiana, exponencial, entre otras. Esta selección dependerá de la aplicación en la que se emplee, la percepción del concepto representado y el nivel de detalle requerido. En [14] se ofrecen un resumen con varias definiciones básicas relacionadas a este tema.
Se le denomina discretización de datos al proceso que tiene como objetivo dividir algunas características continuas en un pequeño número de intervalos, que logren mantener una adecuada coherencia de clase [38]. Este tipo de discretización, conocido como discretización clásica, tiene como característica que los diferentes intervalos que se formen serán excluyentes. Sin embargo, este rasgo introduce una dificultad en la extracción del conocimiento si los expertos entrevistados no tienen el mismo criterio en cuanto a los valores que definirán los intervalos e, incluso, un mismo experto pudiera tener dudas al determinar con precisión el valor que separará un intervalo de otro. El proceso de discretización es imprescindible realizarlo cuando se utilizan herramientas para la inducción del árbol como el algoritmo ID3 que sólo trabaja con atributos nominales o discretos.
Para resolver la desventaja mencionada anteriormente en el proceso de discretización se combina este proceso con la lógica difusa con el objetivo de emular mejor el pensamiento y conocimiento de los expertos. Los valores numéricos adquiridos del proceso serán llevados a categorías difusas. De esta forma, los límites entre categorías podrán quedar solapados, como expresión de la incertidumbre que puede manifestarse al definirlos. Además, permitirá que los expertos puedan asignarle a cada valor en el universo de discurso, un valor de pertinencia acorde a su criterio, para cada una de las categorías definidas de las variables bajo análisis.
Tabla de síntomas de fallos
Una herramienta que permite hacer uso del conocimiento de los expertos para definir la relación entre las distintas variables que caracterizan los fallos del proceso, es la denominada tabla o matriz de síntomas de fallos. Esta se basa en agrupar, en forma de tabla, todos los síntomas que deriven en cada uno de los estados de operación del proceso. Algunas características a destacar son que: la tabla no puede quedar vacía; debe recoger al menos un síntoma por variable para cada fallo que se desee diagnosticar y la unión de todos los síntomas plasma todas las categorías de todas las variables que han sido definidas. De esta manera, toda la información que se necesita para el diagnóstico será tomada del conocimiento de los expertos y no será necesario contar con una base de datos de entrenamiento.
Árboles de decisión
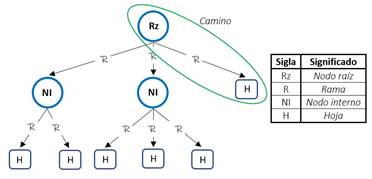
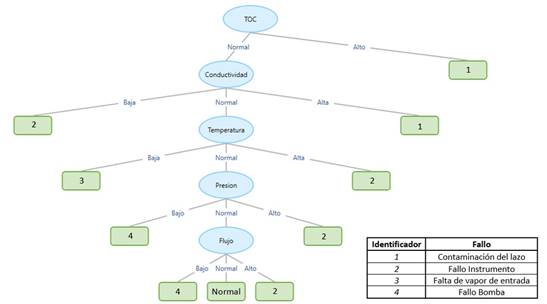
Un árbol de decisión es un clasificador expresado como una partición recursiva del espacio muestral. El árbol está compuesto por nodos: un nodo raíz, que es al cual no le llega ninguna arista o rama, mientras que al resto de estos les llega una sola rama entrante. Los nodos que tienen varias ramas de salida se llaman nodos internos o de encuesta y los nodos que no tienen ramas de salida se llaman hojas o nodos de decisión [12]. A la unión entre un nodo y el siguiente se le denomina rama y a cada conjunto de nodos y ramas desde el nodo raíz hasta cada una de las hojas se le llama camino. La Fig. 1 presenta un ejemplo de un árbol de decisión para ilustrar su estructura:
Inducción del árbol de decisión
La inducción del árbol de decisión consiste en el desarrollo de un conjunto de reglas de clasificación que permita determinar la clase (estado de operación de proceso) a la que pertenecen una serie de objetos (variables) dados sus atributos (valores sensados de las variables u observaciones) [39].
Existen diferentes algoritmos para llevar a cabo esta tarea, algunos de ellos son ID3, C4.5 y CART [12]. En nuestro caso se seleccionó al ID3 por simplicidad y lo bien que representa la relación real que existe entre las variables y los estados de operación del proceso (clases), lo que facilita la comprensión del árbol de decisión resultante [39]. Este algoritmo usa como criterio de división del conjunto de entrenamiento (tabla de síntomas de fallo) a la ganancia de información y como criterio de parada que todos los síntomas pertenezcan al mismo estado de operación o que la máxima ganancia de información no sea mayor que 0.
El procedimiento de inducción del árbol de decisión con el algoritmo ID3 según [39] es el siguiente: sea 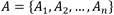 un conjunto de n variables donde a cada variable A
i
le corresponde un conjunto
un conjunto de n variables donde a cada variable A
i
le corresponde un conjunto 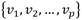 de categorías. Sea
de categorías. Sea 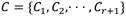 un conjunto de r + 1 estados de operación de los cuales r estados serán fallos y el restante es la operación normal del sistema. Cada estado de operación estará caracterizado por uno o varios síntomas y cada síntoma del conjunto de entrenamiento S estará definido por una combinación única de categorías por cada una de las n variables del sistema. Sea T una prueba o evaluación realizada sobre el conjunto de los síntomas S con posibles salidas
un conjunto de r + 1 estados de operación de los cuales r estados serán fallos y el restante es la operación normal del sistema. Cada estado de operación estará caracterizado por uno o varios síntomas y cada síntoma del conjunto de entrenamiento S estará definido por una combinación única de categorías por cada una de las n variables del sistema. Sea T una prueba o evaluación realizada sobre el conjunto de los síntomas S con posibles salidas 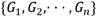 , una salida por cada variable del sistema. Si se define T como el criterio de división del conjunto de entrenamiento, en este caso la ganancia de información, entonces se obtendrá como resultado la variable Ai que maximiza dicha ganancia de información. Luego, Ai se tomará como el nodo raíz del árbol actual y el conjunto S se dividirá en p subconjuntos, uno por cada categoría asociada a Ai. Cabe puntualizarse que una vez una variable sea seleccionada como raíz de un árbol, ya no se podrá volver a tener en cuenta en las siguientes pruebas que se realicen. Entonces, si cada uno de los p subconjuntos de S puede ser sustituido por un árbol de decisión, se logrará un árbol de decisión para todo S. O sea, por cada Sj se generará un sub-árbol de decisión y la unión de todos estos sub-árboles darán lugar al árbol de decisión final. T se continuará realizando recursivamente hasta que se cumplan cualquiera de las condiciones de parada del algoritmo ID3 mencionadas anteriormente.
, una salida por cada variable del sistema. Si se define T como el criterio de división del conjunto de entrenamiento, en este caso la ganancia de información, entonces se obtendrá como resultado la variable Ai que maximiza dicha ganancia de información. Luego, Ai se tomará como el nodo raíz del árbol actual y el conjunto S se dividirá en p subconjuntos, uno por cada categoría asociada a Ai. Cabe puntualizarse que una vez una variable sea seleccionada como raíz de un árbol, ya no se podrá volver a tener en cuenta en las siguientes pruebas que se realicen. Entonces, si cada uno de los p subconjuntos de S puede ser sustituido por un árbol de decisión, se logrará un árbol de decisión para todo S. O sea, por cada Sj se generará un sub-árbol de decisión y la unión de todos estos sub-árboles darán lugar al árbol de decisión final. T se continuará realizando recursivamente hasta que se cumplan cualquiera de las condiciones de parada del algoritmo ID3 mencionadas anteriormente.
El criterio de división a emplear en la inducción del árbol de decisión es el de la ganancia de información [12]:
Donde: I(S) es la información necesaria para que el árbol pueda clasificar una clase cualquiera en S:
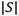 : Cantidad de síntomas de fallo en S.
: Cantidad de síntomas de fallo en S.
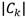 : Cantidad de síntomas de fallo en S que pertenecen al k-ésimo estado de operación.
: Cantidad de síntomas de fallo en S que pertenecen al k-ésimo estado de operación.
Y E(Aj, S es la información esperada que se necesita para que Aj sea la raíz del árbol:
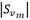 : Cantidad de síntomas de fallo en S donde Aj toma el valor vm.
: Cantidad de síntomas de fallo en S donde Aj toma el valor vm.
Los pasos antes descritos se resumen en Algoritmo 1.
Algoritmo 1. Pseudocódigo para la inducción del árbol de decisión propuesta [N DT_Induction (S)]
N DT_Induction (S);
Input: S (Tabla de síntomas de fallos);
Output: N (Nodo del árbol de decisión);
Inferencia del árbol de decisión
La inferencia en un árbol de decisión clásico define el proceso con el cual, dado una observación de los atributos del sistema, se llega a una clasificación a partir del árbol de decisión ya inducido. Este procedimiento comienza evaluando la variable ubicada en el nodo raíz, la rama que resulte de esta operación dará lugar al nuevo nodo a evaluar y así sucesivamente hasta llegar a un nodo hoja, la clase correspondiente a este último nodo será la clasificación resultante de este procedimiento.
De lo anterior resalta que la forma clásica de inferencia realiza las pruebas a los nodos para un solo camino del árbol; sin embargo, al hacer uso de la lógica difusa, se le deben realizar algunas modificaciones a ese método. De acuerdo al algoritmo planteado en [40] el valor de cada atributo será evaluado en el nodo correspondiente para determinar el valor de pertenencia a cada una de las categorías, de forma tal que todos los caminos del árbol de decisión intervengan en la clasificación; correspondiendo el resultado final a la clase que posea la hoja con mayor valor de pertenencia.
Para todo árbol de decisión inducido se pueden definir:
Teniendo en cuenta las definiciones anteriores y siguiendo lo planteado en [39], la inferencia difusa de un árbol de decisión puede llevarse a cabo en cuatro pasos. Primero, se evalúa la muestra correspondiente x i de la observación en cada categoría difusa A ij para obtener el valor de pertenencia μ ij . Luego, por cada uno de los n caminos del árbol, se multiplican los valores de pertenencia y se le asigna el resultado a la hoja H p de dicho camino. Posteriormente se suman los valores de las hojas correspondientes al estado de operación O q . Por último, se toma como clasificación final al estado de operación que mayor sumatoria obtuvo. Este procedimiento se puede resumir tal y como se muestra en el Algoritmo 2.
Algoritmo 2. Pseudocódigo para la inducción del árbol de decisión propuesta [OE DT_Inference (Obs)]
OE DT_Inference (Obs);
Input: Obs: observación;
Output: OE: estado de operación resultante;
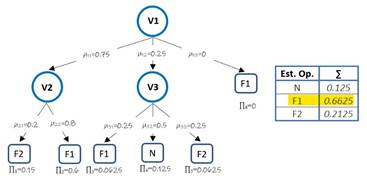
Suponiendo que se tiene un proceso en el que se miden tres variables (V1; V2; V3) y se definen tres estados de operación: el estado normal (N) y dos fallos (F1; F2); al llevar a cabo el método anterior se obtiene lo presentado en la Fig. 2, donde la clasificación final resultó ser el fallo F1 con un 66.25 % de certeza.
Este procedimiento, a diferencia del de inducción del árbol de decisión que solo se aplica una vez se realiza repetidamente cada una determinada cantidad de muestras de las variables medidas.
Estructura del esquema de monitoreo
En este trabajo se propone un esquema de desarrollo en el que el árbol de decisión (técnica de monitoreo) es configurado en una aplicación fuera de línea. Luego, la configuración resultante es exportada en un fichero con formato PMML el cual será utilizado por una segunda aplicación. Dicha aplicación (aplicación en línea) es la que realiza el monitoreo en línea del proceso, a partir de la obtención de los valores de las variables directamente del sistema de supervisión, control y adquisición de datos (SCADA por sus siglas en inglés) mediante el protocolo OPC (Open Platform Communication). Una representación del esquema empleado se presenta en la Fig. 3.
La información generada por la aplicación que realiza la configuración del proceso de monitoreo consiste en: la identificación de las variables del SCADA que serán utilizadas para el monitoreo y los fallos que se desean diagnosticar, las transformaciones realizadas a las variables seleccionadas y la definición y diseño de los modelos utilizados para realizar la tarea de diagnóstico. El formato PMML permite darles persistencia a los procedimientos anteriores, por lo que se utilizará como soporte para transmitir la información del modelo configurado a la aplicación que realiza las tareas de monitoreo en línea.
Metodología propuesta
A continuación, se presentarán la metodología propuesta en este trabajo:
Entrevista a los expertos: Como hemos estado mencionando desde el inicio, una etapa fundamental para el diseño del diagnosticador consiste en la entrevista a los expertos. El objetivo fundamental de este proceso consiste en obtener la base de conocimiento con la cual se construirá el árbol de decisión.
Configuración del esquema de diagnóstico: En esta etapa se lleva a cabo la tarea de configuración fuera de línea del algoritmo seleccionado para el diagnóstico. Esta va a permitir realizar ajustes del esquema desarrollado antes de su puesta en funcionamiento en línea.
Uso en línea del esquema de diagnóstico:
Importar del fichero PMML: Para usar el modelo seleccionado se carga en la aplicación en línea el fichero en formato PMML con la información del árbol de decisión configurado fuera de línea para su uso en el sistema.
Comunicar la aplicación con el sistema SCADA: Haciendo uso del protocolo OPC, se realiza la conexión de la aplicación con el sistema SCADA. El objetivo de este paso es enlazar las variables que se emplearán en el diagnóstico con sus muestras correspondientes en el sistema de monitoreo.
Realizar la inferencia del árbol de decisión: Finalmente, solo queda hacer uso del árbol de decisión para clasificar el conjunto de muestras que se va obteniendo de las variables del sistema. Para cada uno de esos conjuntos (u observaciones) se tendrá el estado de operación del sistema en ese momento, ya sea estado normal o un determinado fallo.
Resultados
La metodología propuesta fue aplicada a un proceso real, específicamente en la planta de tratamiento de agua para inyección de la industria farmacéutica Citostáticos perteneciente a la empresa AICA, ubicada en la provincia La Habana, Cuba.
El proceso consiste en un sistema para guardar y distribuir agua purificada para inyección; garantizando un suministro constante y fiable dentro del sistema de recirculación en sí, así como en todos los puntos de uso. El mismo posee varios modos de operación, pero para la tarea de diagnóstico se estará trabajando específicamente en el modo de producción principal. El sistema cuenta con una bomba de carga de presión que alimenta el circuito de recirculación con el agua del depósito para que pueda tomarse de los puntos de uso. En la línea de retorno del circuito de recirculación se monitorizan el flujo, la presión, la conductividad, TOC y la temperatura (variables a utilizar en el diagnóstico de fallos). Los datos operativos del proceso se recogen en la Tabla 1.
Tabla 1 Datos operativos del proceso bajo estudio
| Variables | Unidad de Med. | Valor |
|---|---|---|
| Flujo en la línea de retorno | m
|
4 |
| Presión en la línea de retorno | bar | aprox. 1.4 |
| Temperatura de trabajo |
|
18 |
| TOC | ppb | < 80 |
| Conductividad a 25ºC | μS/cm | < 1.3 |
Prueba de diagnóstico real
Entrevista con los expertos.
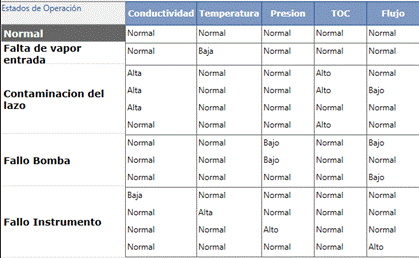
Según los expertos del sistema los fallos que más suelen afectar el proceso son: Fallo instrumento, Contaminación del lazo, Falta de vapor de entrada y Fallo de la bomba. En la Tabla 2 se recogen algunas de sus características.
Tabla 2 Características de los fallos a diagnosticar
| Fallos a diagnosticar | Características |
|---|---|
| Fallo instrumento | Indica que los instrumentos de medición empleados están arrojando valores fuera del rango lógico del canal analógico. |
| Contaminación del lazo | El agua purificada tiene que cumplir con ciertas normas de calidad, una de ellas es que el valor de TOC no puede sobrepasar cierto límite, pues cuando ello ocurre significa que el agua está contaminada y, por tanto, ya no es adecuada para su uso. Similarmente ocurre con la variable conductividad. |
| Falta de vapor de entrada | Significa que no está llegando al sistema el vapor industrial que viene de la línea de la caldera y que se requiere en el intercambiador de calor (calentador). |
| Fallo de la bomba | Ocurre cuando la bomba encargada de mantener la recirculación del agua en el lazo falla y no mantiene el flujo (ni la presión) establecido. |
Por otro lado, las variables asociadas a estos fallos, como se mencionó anteriormente, son las que se encuentran en la línea de retorno del circuito de recirculación: flujo, presión, conductividad, TOC y temperatura. La discretización difusa de las mismas en funciones de pertenencia de tipo trapezoidal aparece en la Tabla 3.
Tabla 3 Discretización difusa de las variables para el diagnóstico
| Variables | Categorías difusas | Parámetros (a; b; c; d) |
|---|---|---|
| Flujo en la línea de retorno (m
|
Bajo | (( ∞; ( ∞; 1; 1.2) |
| Normal | (1; 1.2; 4; 5) | |
| Alto | (4; 5; ∞; ∞) | |
| Presión en la línea de retorno (bar) | Baja | (( ∞; ( ∞; 1; 1.1) |
| Normal | (1; 1.1; 2.3; 2.5) | |
| Alta | (2.3; 2.5; ∞; ∞) | |
| Temperatura de trabajo (
|
Baja | (( ∞; ( ∞; 10; 15) |
| Normal | (10; 15; 20; 25) | |
| Alta | (20; 25; ∞; ∞) | |
| TOC (ppb) | Normal | (( ∞; ( ∞; 50; 80) |
| Alto | (50; 80; ∞; ∞) | |
| Conductividad a 25ºC (μS/cm) | Baja | (( ∞; ( ∞; 0.3; 0.4) |
| Normal | (0.3; 0.4; 0.97; 1.3) | |
| Alta | (0.97; 1.3; ∞; ∞) |
El último paso de la entrevista fue la conformación de la base de conocimiento (tabla de síntomas de fallos) que se muestra en la Fig. 4.
Inducción del árbol de decisión.
El procedimiento de inducción del árbol de decisión arrojó el resultado mostrado en la Fig. 5, de donde se aprecia que para este proceso todas las variables definidas por los expertos fueron necesarias en el diagnóstico. Resulta interesante hacer un paréntesis en este caso y mencionar que, si bien la tabla de síntomas de fallos constituye una base de reglas con la que se pudiera realizar el diagnóstico directamente, o sea, sin la necesidad de pasar por el trabajo de confeccionar el árbol de fallos; es fácil darse cuenta de la gran ventaja que constituye la representación gráfica, pues como se observa en la Fig. 5, cualquier trabajador de la planta de tratamiento puede comprender de forma rápida y sencilla los distintos comportamientos de las variables que llevan a los fallos definidos, sin la necesidad de tener contacto con expertos cada vez que se requiera de esta información.
Inferencia del árbol de fallos.
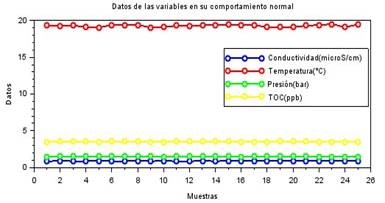
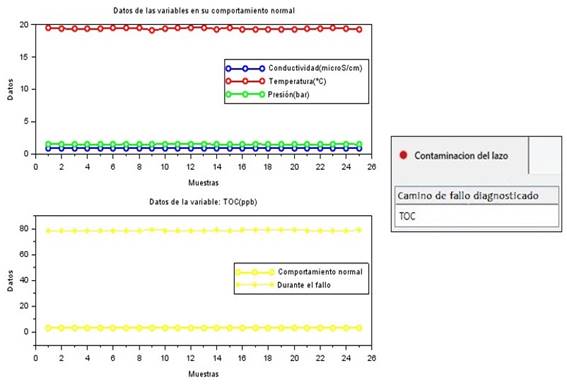
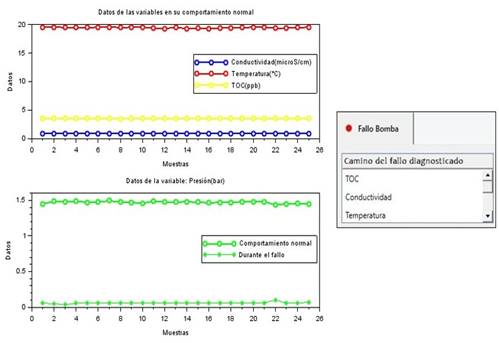
Algunos de los resultados del diagnóstico de los fallos en la planta se observan en las Fig. 6-8, a la izquierda se encuentra una gráfica con una muestra de los datos de las variables que llevaron al fallo diagnosticado y a la derecha una parte de la vista de la aplicación empleada para esta tarea. La Tabla 4 resume una descripción de lo que ocurre en estas figuras.
Tabla 4 Resumen de los aspectos observados en las figuras 6, 7, 8.
| Estado de Operación | Notas |
|---|---|
| Normal | Los datos se encuentran dentro de la categoría Normal para cada una de las variables. |
| Contaminación del lazo | Los datos del TOC están muy por encima del valor esperado, por lo que corresponden a la categoría Alto. (Ver cuarto síntoma del fallo en la Fig. 4). |
| Fallo de la bomba | Si bien los datos de TOC, Conductividad y Temperatura entran en la categoría Normal; los de la Presión son menores a 1.1 𝑏𝑎𝑟, lo que hace que pertenezcan a la categoría Baja. (Ver segundo síntoma del fallo en la Fig. 4). |
Conclusiones
Con la presente investigación se obtuvo una nueva metodología para el diagnóstico de fallos basado en árboles de decisión y lógica difusa. Dicha metodología demuestra:
las facilidades de la lógica difusa aplicada a la etapa de discretización de las variables; por cuanto es capaz de simular mejor el pensamiento de los expertos y, permitir con ello, hacer frente a los problemas relacionados a la incertidumbre que surge cuando se definen rangos de las variables.
las capacidades que brinda el uso de tablas de síntomas de fallos. Debido a que los expertos cuentan con grandes conocimientos relacionados a la tarea de diagnóstico, pero muchas veces no saben representarlos adecuadamente. Unido al hecho de que da la posibilidad de no necesitar una gran base de datos que sea cien por ciento accesible e íntegra para el entrenamiento del árbol de decisión.
las potencialidades del estándar PMML. El cual permite el intercambio de modelos de inteligencia artificial que, a su vez, posibilita el desarrollo de un esquema de monitoreo de dos etapas: configuración y monitoreo en línea.
la sencillez de comprensión de los árboles de decisión para tareas de diagnóstico. En vez de expresar el conocimiento de los expertos mediante una base de reglas, se opta por hacer una representación gráfica de un árbol de decisión, a fin de aprovechar las ventajas de esta técnica en cuanto a la facilidad de compresión que les ofrece a los trabajadores que tengan que utilizar la herramienta. Además, con el ejemplo de simulación se demostró que a veces esta técnica contribuye a disminuir los costos del diagnóstico, al no incluir aquellas variables que realmente no sean necesarias para la realización de esta tarea.