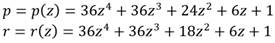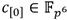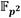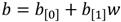Introducción
Los emparejamientos bilineales sobre curvas elípticas se han erigido como una potente herramienta que permite construir diversos protocolos de seguridad para brindar vías de solución a varios problemas existentes en la criptografía. Entre los ejemplos más notables se deben mencionar el protocolo tripartito de acuerdo de claves con una sola ronda de mensajes propuesto en [1] y el protocolo de acuerdo de claves basado en identidad sin interacción entre las partes presentado en [2]. Igualmente se han dado a conocer esquemas de cifrado basado en identidad [3, 4, 5], esquemas de firma digital de pequeña longitud [6], así como esquemas de cifrado basado en atributos [7] y esquemas de cifrado homomórfico [8]. Sin embargo, el proceso de cálculo de un emparejamiento bilineal constituye una tarea compleja con un costo en cuanto a tiempo de ejecución que supera al de las operaciones involucradas en criptosistemas convencionales como RSA1 y ECC2. Por ejemplo, para una curva elíptica definida sobre un campo finito de 256 bits, se ha reportado que calcular una multiplicación escalar (operación principal en ECC) resulta hasta 30 veces más rápido que efectuar el cálculo de un emparejamiento bilineal [9, 10]. Esto ha motivado el curso de numerosas investigaciones enfocadas en desarrollar formulaciones algorítmicas y evaluar estrategias de implementación que permitan obtener soluciones eficientes para el cálculo de emparejamientos bilineales. Especial atención han tenido las implementaciones para sistemas empotrados donde generalmente los recursos de procesamiento son limitados en comparación con los de una computadora de propósito general.
En la literatura se han propuesto varias implementaciones sobre sistemas empotrados de soluciones enfocadas en el cálculo de emparejamientos bilineales o de sus principales operaciones aritméticas. Algunas de estas soluciones han sido desarrolladas en software [11, 12, 13, 14, 15], y otras basadas en diseños hardware [16, 17, 18, 19, 20, 21]. En el despliegue de las soluciones software ha predominado el empleo de procesadores ARM debido a su popularidad en el campo de los sistemas empotrados. En este caso, los mejores resultados de rendimiento en cuanto a tiempo de ejecución se han obtenido a partir de la optimización de operaciones en lenguaje ensamblador [11], el empleo de instrucciones SIMD [12, 13, 14] y de estrategias de procesamiento multinúcleo [15].
Las soluciones basadas en hardware exhiben dos tipos de implementaciones: rígidas [17, 18, 21] y flexibles [16, 19, 22, 23]. Las primeras persiguen obtener buenos resultados de tiempo al optimizar las implementaciones para un tipo de emparejamiento y conjunto de parámetros específicos. En cambio, las soluciones flexibles, ofrecen cierto nivel de aceleración, pero manteniendo facilidades para implementar diferentes tipos de emparejamientos, así como modificar los parámetros asociados a la curva elíptica y a las operaciones aritméticas subyacentes. Esto constituye una ventaja importante cuando se requiere actualizar una primitiva criptográfica para satisfacer nuevos requisitos de seguridad.
Una alternativa para la obtención de implementaciones basadas en hardware con cierto grado de flexibilidad consiste en emplear estrategias de diseño híbrido hardware/software. De esta forma, se implementan en hardware aquellas operaciones básicas que sean exigentes en cuanto a tiempo, mientras que las operaciones de alto nivel y el control del flujo de procesamiento se llevan a cabo en un procesador de propósito general. Este enfoque ha sido explorado en [20] mediante la interconexión de un procesador ARM Cortex-M0+ encargado de ejecutar la parte software y un coprocesador implementado en un ASIC para la aritmética de campo finito que es acelerada mediante hardware. La arquitectura de este coprocesador se basa en el empleo de estructuras de pipeline internas que permiten simultanear las operaciones básicas de multiplicación y acumulación a medida que se procesan las palabras (de 32 bits) de los operandos. Con esto, los autores de [20] alcanzan un nivel de aceleración de la aritmética de campo que demuestra la pertinencia del enfoque de diseño híbrido al obtener un rendimiento seis veces superior en el cálculo de un emparejamiento respecto a una solución puramente software desarrollada sobre el propio procesador ARM Cortex-M0+.
Teniendo en cuenta lo anterior, en este trabajo se propone explotar en mayor medida la paralelización de operaciones mediante hardware extendiendo el alcance de las estructuras de pipeline. En este caso se trata no sólo de simultanear las operaciones de palabra internas a una operación de campo finito, sino que, a partir de identificar el alto grado de paralelismo presente en el cálculo de un emparejamiento, se propone además estructurar el diseño de un pipeline externo que permita solapar la ejecución de varias operaciones de campo. Igualmente se pretende explorar el empleo de un ancho de palabra de 64 bits, lo cual se traduce en una reducción del número de operaciones básicas que se requieren efectuar a nivel de palabra para completar una operación de campo finito. Estas ideas han dado origen a la implementación del coprocesador que se describe a lo largo del presente trabajo, cuyo propósito radica en desarrollar una solución híbrida hardware/software para el cálculo de emparejamientos bilineales que logre mejorar el rendimiento de soluciones equivalentes reportadas en el estado del arte.
El contenido expuesto en el resto del documento ha sido estructurado de la siguiente forma: La Sección 2 presenta una breve introducción al emparejamiento Ate óptimo sobre curvas de Barreto-Naehrig. En la Sección 3 y la Sección 4 se discuten los aspectos relacionados con la aritmética de curva y la aritmética de campo requeridas en el cálculo de un emparejamiento, enfatizando las oportunidades de paralelismo existentes en cada caso. La Sección 5 aborda el proceso de implementación del coprocesador propuesto en este trabajo, mientras que en la Sección 6 se analiza el impacto del mismo en el rendimiento de un emparejamiento. Finalmente en la Sección 7 se brindan las consideraciones finales.
Emparejamiento ate-óptimo
La mayoría de las implementaciones prácticas enfocadas en el cálculo eficiente de emparejamientos bilineales están basadas en el emparejamiento Ate-óptimo [24]. En particular, la variante definida sobre curvas de Barreto-Naehrig [25] constituye una de las más extendidas en la literatura por ser de las alternativas más eficientes para satisfacer originalmente un nivel de seguridad de 128 bits [26].
Las curvas de Barreto-Naehrig conforman una de las familias de curvas elípticas conocidas como curvas amigables [27] para el cálculo de emparejamientos bilineales. En este caso se trata de curvas descritas mediante la expresión 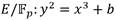 que poseen orden primo r y grado de incrustación k = 12, donde la característica p del campo finito subyacente y el orden de la curva r son parametrizados mediante los siguientes polinomios (1):
que poseen orden primo r y grado de incrustación k = 12, donde la característica p del campo finito subyacente y el orden de la curva r son parametrizados mediante los siguientes polinomios (1):
El parámetro z Є ℤ debe seleccionarse de manera que p = p(z) y r = r(z) sean números primos con el tamaño adecuado para satisfacer el nivel de seguridad deseado. Al mismo tiempo, es determinante seleccionar un valor de z que garantice que el primo p resultante conduzca a la construcción de la extensión 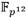 con propiedades favorables para realizar operaciones aritméticas de forma eficiente [28]. En este trabajo se emplea el valor z = -408000000000000116 propuesto en [29] como la mejor opción para proporcionar una fortaleza de 128 bits de seguridad equivalente a partir de generar valores de p y r de 254 bits.
con propiedades favorables para realizar operaciones aritméticas de forma eficiente [28]. En este trabajo se emplea el valor z = -408000000000000116 propuesto en [29] como la mejor opción para proporcionar una fortaleza de 128 bits de seguridad equivalente a partir de generar valores de p y r de 254 bits.
Por otra parte, una de las propiedades más útiles de las curvas de Barreto-Naehrig radica en la existencia de una curva 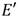 isomórfica con E que permite trasladar gran parte de las operaciones involucradas en el cálculo del emparejamiento desde
isomórfica con E que permite trasladar gran parte de las operaciones involucradas en el cálculo del emparejamiento desde 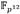 hacia la extensión de menor grado
hacia la extensión de menor grado 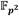 . La ecuación de
. La ecuación de 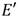 es
es 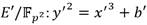 , con
, con 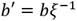 o
o 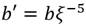 donde ξ es un no residuo cuadrático y no residuo cúbico en
donde ξ es un no residuo cuadrático y no residuo cúbico en 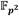 . Sea
. Sea 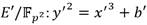 , el mapa
, el mapa 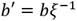 que transforma puntos de
que transforma puntos de 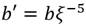 (
(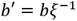 ) en puntos de E(
) en puntos de E(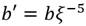 ) es
) es 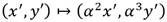 [30]. De esta forma, sean E y
[30]. De esta forma, sean E y 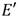 una curva de Barreto-Naehrig y su curva isomórfica sobre
una curva de Barreto-Naehrig y su curva isomórfica sobre 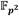 respectivamente y téngase
respectivamente y téngase 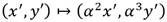 ,
, 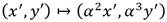 junto al operador de Frobenius
junto al operador de Frobenius 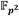 , el emparejamiento Ate-óptimo en curvas de Barreto-Naehrig (AteOpt-BN) [24] se puede expresar como:
, el emparejamiento Ate-óptimo en curvas de Barreto-Naehrig (AteOpt-BN) [24] se puede expresar como:
Para materializar el cálculo de la ecuación (2) se emplea el Algoritmo 1, el cual se basa en las contribuciones realizadas por Miller en [31, 32]. El bucle comprendido entre las líneas 2 y 9 se encarga de calcular el valor 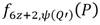 . En tanto, la secuencia que se extiende desde el paso 10 hasta el paso 14 corresponde al ajuste que se aplica sobre el valor
. En tanto, la secuencia que se extiende desde el paso 10 hasta el paso 14 corresponde al ajuste que se aplica sobre el valor 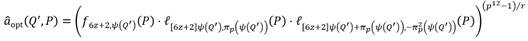 para garantizar que el resultado final satisfaga las propiedades no degenerativa y de bilinealidad de un emparejamiento. No es difícil verificar que al término del bucle de Miller, junto con
para garantizar que el resultado final satisfaga las propiedades no degenerativa y de bilinealidad de un emparejamiento. No es difícil verificar que al término del bucle de Miller, junto con 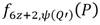 , se obtiene el punto
, se obtiene el punto 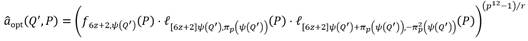 . Esto permite comprobar que las líneas involucradas en las multiplicaciones del tipo
. Esto permite comprobar que las líneas involucradas en las multiplicaciones del tipo 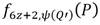 de los pasos 11 y 14 en efecto corresponden a las líneas
de los pasos 11 y 14 en efecto corresponden a las líneas 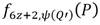 y
y 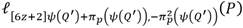 respectivamente.
respectivamente.
Vale destacar que la variable f donde se va acumulando el resultado, así como las líneas secantes y tangentes que se evalúan durante la ejecución del algoritmo, son elementos de 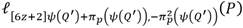 . No obstante, en el caso particular de las líneas, los elementos de
. No obstante, en el caso particular de las líneas, los elementos de  resultantes poseen la mitad de sus coeficientes con valor cero. Esto permite efectuar las operaciones del tipo f · l, (P) mediante un caso especial de multiplicación denominada multiplicación dispersa que resulta más eficiente que una multiplicación genérica en
resultantes poseen la mitad de sus coeficientes con valor cero. Esto permite efectuar las operaciones del tipo f · l, (P) mediante un caso especial de multiplicación denominada multiplicación dispersa que resulta más eficiente que una multiplicación genérica en 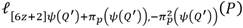 .
.
Exponenciación final
El paso 15 del Algoritmo 1 se conoce como etapa de exponenciación final. Para acelerar el cálculo de esta etapa se ha adoptado el método propuesto en [33], el cual se basa en descomponer en factores el exponente  en una parte denominada exponente fácil y otra conocida como exponente difícil (3):
en una parte denominada exponente fácil y otra conocida como exponente difícil (3):
El cálculo de 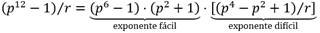 se divide a su vez en
se divide a su vez en 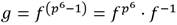 y
y 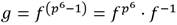 . Dado que
. Dado que 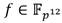 se representa como un binomio con coeficientes en
se representa como un binomio con coeficientes en 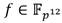 , el término
, el término 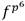 se obtiene como el conjugado
se obtiene como el conjugado 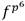 de f. Las restantes operaciones involucradas en el cálculo de la parte fácil de la exponenciación final incluyen una inversa y dos multiplicaciones en
de f. Las restantes operaciones involucradas en el cálculo de la parte fácil de la exponenciación final incluyen una inversa y dos multiplicaciones en 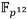 , así como una exponenciación a la potencia p2, la cual se realiza a un costo relativamente bajo mediante el operador de Frobenius. Es importante destacar que el elemento
, así como una exponenciación a la potencia p2, la cual se realiza a un costo relativamente bajo mediante el operador de Frobenius. Es importante destacar que el elemento 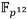 resultante de elevar f al exponente (p
6
- 1) es un elemento unitario [34]. Los elementos de este tipo forman un subgrupo de
resultante de elevar f al exponente (p
6
- 1) es un elemento unitario [34]. Los elementos de este tipo forman un subgrupo de 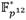 , por lo que cualquier operación subsiguiente que se realice sobre g resulta en otro elemento unitario. Esto resulta favorable para la implementación de la parte difícil de la etapa de exponenciación final ya que, en primer lugar, permite sustituir en lo adelante las operaciones de inversa por conjugaciones. O sea, para todo elemento unitario
, por lo que cualquier operación subsiguiente que se realice sobre g resulta en otro elemento unitario. Esto resulta favorable para la implementación de la parte difícil de la etapa de exponenciación final ya que, en primer lugar, permite sustituir en lo adelante las operaciones de inversa por conjugaciones. O sea, para todo elemento unitario 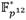 se cumple que
se cumple que 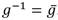 . Por otra parte, determinar el cuadrado de elementos unitarios resulta más eficiente que una operación de cuadrado genérica en
. Por otra parte, determinar el cuadrado de elementos unitarios resulta más eficiente que una operación de cuadrado genérica en 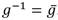 .
.
Para calcular la parte difícil 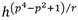 se representa el exponente en base p como
se representa el exponente en base p como 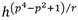 . Los coeficientes Хi se expresan en función del parámetro z de Barreto-Naehrig de la siguiente forma:
. Los coeficientes Хi se expresan en función del parámetro z de Barreto-Naehrig de la siguiente forma:
A partir de la ecuación (4) se tiene que 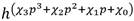 se convierte en (5):
se convierte en (5):
En la ecuación (5) primero se calculan los términos h
z
, 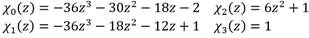 y
y 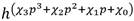 . Seguidamente, las operaciones de exponenciación a las potencias p, p2 y p3 se calculan mediante el operador de Frobenius. Las fracciones involucradas en los términos y1 y del y3 al y6 representan inversas de campo que, como se ha mencionado, son sustituidas por conjugadas gracias a las propiedades de los elementos unitarios. Finalmente, la expresión
. Seguidamente, las operaciones de exponenciación a las potencias p, p2 y p3 se calculan mediante el operador de Frobenius. Las fracciones involucradas en los términos y1 y del y3 al y6 representan inversas de campo que, como se ha mencionado, son sustituidas por conjugadas gracias a las propiedades de los elementos unitarios. Finalmente, la expresión 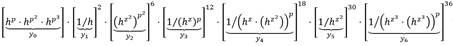 se evalúa de manera eficiente mediante una cadena de suma vectorial de longitud mínima [35].
se evalúa de manera eficiente mediante una cadena de suma vectorial de longitud mínima [35].
Aritmética de curvas
Como se aprecia en el Algoritmo 1 las operaciones internas al bucle de Miller involucran la evaluación de líneas y el cálculo de puntos sobre la curva isomórfica 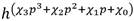 . Emplear el sistema de coordenadas adecuado para representar los puntos de curva es crucial para obtener buenos resultados de rendimiento. En general, la representación de puntos en coordenadas proyectivas conduce a implementaciones de la aritmética de curva con un menor costo computacional en comparación al que se obtiene mediante el empleo de la representación tradicional en coordenadas afines [36].
. Emplear el sistema de coordenadas adecuado para representar los puntos de curva es crucial para obtener buenos resultados de rendimiento. En general, la representación de puntos en coordenadas proyectivas conduce a implementaciones de la aritmética de curva con un menor costo computacional en comparación al que se obtiene mediante el empleo de la representación tradicional en coordenadas afines [36].
Un punto 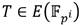 en coordenadas proyectivas se representa como
en coordenadas proyectivas se representa como 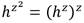 con
con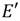 . El mapa
. El mapa 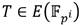 permite trasladar un punto en coordenadas proyectivas a su representación en coordenadas afines (x
T
, y
T
) 𝑥 𝑇 , 𝑦 𝑇 . Diferentes valores para los parámetros 𝑐 y 𝑑 determinan sistemas de coordenadas proyectivas diferentes. Por ejemplo, los valores c = d = 1 definen el sistema de proyectivas estándares [37], mientras que el empleo de c = 2 y d = 3 conduce a las proyectivas Jacobianas [38]. Estas últimas son precisamente las que han sido seleccionadas en el presente trabajo debido a que en el contexto del emparejamiento AteOpt-BN conducen a formulaciones para la aritmética de puntos con un costo ligeramente menor que las que se obtienen en base a las coordenadas proyectivas estándares.
permite trasladar un punto en coordenadas proyectivas a su representación en coordenadas afines (x
T
, y
T
) 𝑥 𝑇 , 𝑦 𝑇 . Diferentes valores para los parámetros 𝑐 y 𝑑 determinan sistemas de coordenadas proyectivas diferentes. Por ejemplo, los valores c = d = 1 definen el sistema de proyectivas estándares [37], mientras que el empleo de c = 2 y d = 3 conduce a las proyectivas Jacobianas [38]. Estas últimas son precisamente las que han sido seleccionadas en el presente trabajo debido a que en el contexto del emparejamiento AteOpt-BN conducen a formulaciones para la aritmética de puntos con un costo ligeramente menor que las que se obtienen en base a las coordenadas proyectivas estándares.
Suma de puntos y línea secante
Sea E una curva de Barreto-Naehrig y 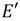 su curva isomórfica junto con el mapa ψ definido en la Sección 2. Téngase
su curva isomórfica junto con el mapa ψ definido en la Sección 2. Téngase 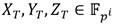 y
y 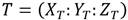 . Asumiendo que
. Asumiendo que 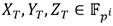 en coordenadas Jacobianas representa cualquier valor intermedio del punto
en coordenadas Jacobianas representa cualquier valor intermedio del punto 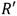 en el Algoritmo 1, la ecuación (10) permite calcular las coordenadas
en el Algoritmo 1, la ecuación (10) permite calcular las coordenadas 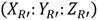 del punto
del punto 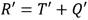 , mientas que la ecuación (7) corresponde al cálculo y evaluación de la línea secante
, mientas que la ecuación (7) corresponde al cálculo y evaluación de la línea secante 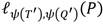 .
.
Se puede apreciar que las ecuaciones (6) y (7) comparten varios términos. Esto permite seguir las recomendaciones de [39] para combinar en un solo procedimiento (Algoritmo 2) los procesos de cálculo de líneas secantes y suma de puntos. Todas las operaciones se realizan en 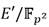 excepto las cuatro multiplicaciones de los pasos del 8 al 11 que corresponden a elementos de
excepto las cuatro multiplicaciones de los pasos del 8 al 11 que corresponden a elementos de 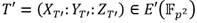 .
.
Doblado de puntos y línea tangente
Partiendo de las mismas premisas del apartado 3.1 es posible definir las ecuaciones (8) y (9) para calcular las coordenadas 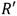 del punto
del punto 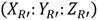 y evaluar la línea tangente
y evaluar la línea tangente 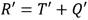 respectivamente.
respectivamente.
En este caso la existencia de términos comunes en ambas ecuaciones también permite formular un único procedimiento para el cálculo combinado de doblado de puntos y evaluación de tangentes sobre la curva elíptica (Algoritmo 3). De igual forma todas las operaciones se realizan en 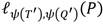 exceptuando las cuatro multiplicaciones en
exceptuando las cuatro multiplicaciones en 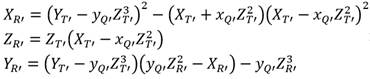 de los pasos del 11 al 14.
de los pasos del 11 al 14.
Torre de campos
Las sentencias del tipo 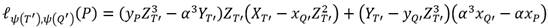 presentes en el algoritmo de Miller corresponden a operaciones de cuadrado y multiplicación de elementos en
presentes en el algoritmo de Miller corresponden a operaciones de cuadrado y multiplicación de elementos en 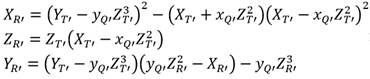 . Es por ello que la forma en que se construya esta extensión de campo es crucial para obtener buenos resultados de rendimiento en el proceso de cálculo de un emparejamiento. En general, los autores de [40] han observado que si el grado k de una extensión
. Es por ello que la forma en que se construya esta extensión de campo es crucial para obtener buenos resultados de rendimiento en el proceso de cálculo de un emparejamiento. En general, los autores de [40] han observado que si el grado k de una extensión 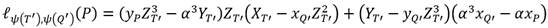 puede expresarse como
puede expresarse como  , entonces es posible representar dicha extensión como una torre de extensiones cuadráticas y cúbicas. En particular, siguiendo las recomendaciones de [28, 41], para la implementación del emparejamiento AteOpt-BN en este trabajo se emplea la torre
, entonces es posible representar dicha extensión como una torre de extensiones cuadráticas y cúbicas. En particular, siguiendo las recomendaciones de [28, 41], para la implementación del emparejamiento AteOpt-BN en este trabajo se emplea la torre 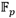 dada por (10):
dada por (10):
Los elementos  ,
, 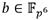 y
y 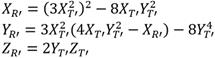 se representan mediante binomios o trinomios según corresponda. De esta forma se tiene que
se representan mediante binomios o trinomios según corresponda. De esta forma se tiene que 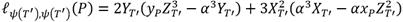 ,
, 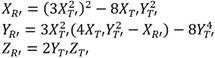 y
y 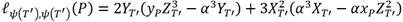 , donde
, donde  ,
, 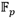 y
y  . Así, para referenciar coeficientes específicos dentro de estas representaciones polinómicas se emplea la misma notación utilizada en [15]. Por ejemplo, en el elemento
. Así, para referenciar coeficientes específicos dentro de estas representaciones polinómicas se emplea la misma notación utilizada en [15]. Por ejemplo, en el elemento 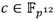 el coeficiente
el coeficiente 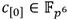 se representaría como
se representaría como 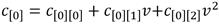 , con
, con 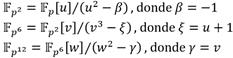 , al tiempo que el coeficiente
, al tiempo que el coeficiente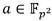 se representaría mediante el binomio
se representaría mediante el binomio 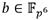 , donde
, donde 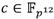 .
.
Uno de los grandes beneficios de utilizar torres de campos radica en que las extensiones de un mismo grado comparten similitud estructural. Esto permite emplear formulaciones algorítmicas similares para implementar aquellas operaciones aritméticas equivalentes en cada una de ellas. Por ejemplo, en la torre de la ecuación (10) el método que se utilice para efectuar multiplicaciones en 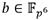 puede adaptarse para multiplicar elementos en
puede adaptarse para multiplicar elementos en 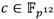 ya que ambas son extensiones cuadráticas. Por otra parte, la recursividad que introducen las torres de campo conduce a que cualquier mejora en el campo base o alguna extensión intermedia se refleje directamente en una mejora de rendimiento de las operaciones en las extensiones siguientes. En este sentido, como se ha visto en las secciones 2 y 3, la mayoría de las operaciones aritméticas involucradas en el cálculo del emparejamiento Ate-óptimo en curvas de Barreto-Naehrig tienen lugar en
ya que ambas son extensiones cuadráticas. Por otra parte, la recursividad que introducen las torres de campo conduce a que cualquier mejora en el campo base o alguna extensión intermedia se refleje directamente en una mejora de rendimiento de las operaciones en las extensiones siguientes. En este sentido, como se ha visto en las secciones 2 y 3, la mayoría de las operaciones aritméticas involucradas en el cálculo del emparejamiento Ate-óptimo en curvas de Barreto-Naehrig tienen lugar en 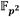 y
y 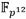 . Además, debido a la estructura de la torre de campos
. Además, debido a la estructura de la torre de campos 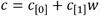 , la aritmética en
, la aritmética en 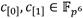 se compone de operaciones aritméticas en
se compone de operaciones aritméticas en 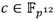 , que a su vez están conformadas por operaciones en
, que a su vez están conformadas por operaciones en 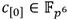 . Por ello, para acelerar el cálculo del emparejamiento AteOpt-BN resulta determinante partir de una implementación eficiente de la aritmética en
. Por ello, para acelerar el cálculo del emparejamiento AteOpt-BN resulta determinante partir de una implementación eficiente de la aritmética en 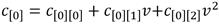 , lo cual es válido también para la implementación de cualquier emparejamiento sobre curvas elípticas con grado de incrustación par [25, 42, 43, 44].
, lo cual es válido también para la implementación de cualquier emparejamiento sobre curvas elípticas con grado de incrustación par [25, 42, 43, 44].
Las operaciones en 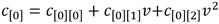 que se requieren implementar en la construcción de la torre de campos de la ecuación (10) son la suma y la resta, la multiplicación, el cuadrado y la inversa multiplicativa. Debido a que los elementos de
que se requieren implementar en la construcción de la torre de campos de la ecuación (10) son la suma y la resta, la multiplicación, el cuadrado y la inversa multiplicativa. Debido a que los elementos de 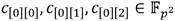 se representan como binomios del tipo
se representan como binomios del tipo 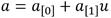 con coeficientes
con coeficientes 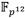 , las operaciones en esta extensión involucran la realización de cálculos subyacentes en el campo base
, las operaciones en esta extensión involucran la realización de cálculos subyacentes en el campo base 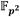 , resultando igualmente necesario implementar operaciones de suma, resta, multiplicación e inversa multiplicativa. En este caso se trata de aritmética modular con números enteros (módulo p), donde, para mayor eficiencia, se ha optado por la representación numérica y el método de reducción de Montgomery [45], así como el algoritmo extendido de Euclides [46] para el cálculo de inversas.
, resultando igualmente necesario implementar operaciones de suma, resta, multiplicación e inversa multiplicativa. En este caso se trata de aritmética modular con números enteros (módulo p), donde, para mayor eficiencia, se ha optado por la representación numérica y el método de reducción de Montgomery [45], así como el algoritmo extendido de Euclides [46] para el cálculo de inversas.
De la aritmética en 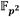 resaltan la multiplicación, el cuadrado y la inversa multiplicativa como las más exigentes en cuanto a costo computacional, siendo la multiplicación la que aparece con mayor frecuencia durante el cálculo de un emparejamiento. Por ejemplo, representando los costos de estas operaciones (multiplicación, cuadrado e inversa multiplicativa en
resaltan la multiplicación, el cuadrado y la inversa multiplicativa como las más exigentes en cuanto a costo computacional, siendo la multiplicación la que aparece con mayor frecuencia durante el cálculo de un emparejamiento. Por ejemplo, representando los costos de estas operaciones (multiplicación, cuadrado e inversa multiplicativa en 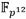 ) como
) como 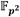 ,
, 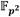 e
e 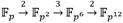 respectivamente, a partir de analizar el algoritmo de Miller (Algoritmo 1) es posible estimar las cantidades requeridas de cada una de estas operaciones para calcular un emparejamiento. Como se ha visto, el bucle de Miller para el emparejamiento AteOpt-BN se basa en el cálculo y evaluación de líneas tangentes y secantes de conjunto con el doblado y la suma de puntos sobre la curva isomórfica
respectivamente, a partir de analizar el algoritmo de Miller (Algoritmo 1) es posible estimar las cantidades requeridas de cada una de estas operaciones para calcular un emparejamiento. Como se ha visto, el bucle de Miller para el emparejamiento AteOpt-BN se basa en el cálculo y evaluación de líneas tangentes y secantes de conjunto con el doblado y la suma de puntos sobre la curva isomórfica 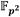 , además de operaciones de cuadrado y multiplicación (multiplicación dispersa) en
, además de operaciones de cuadrado y multiplicación (multiplicación dispersa) en 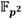 . Del Algoritmo 2 y el Algoritmo 3 es fácil apreciar que cálculo combinado de líneas secantes y suma de puntos requiere de 11
. Del Algoritmo 2 y el Algoritmo 3 es fácil apreciar que cálculo combinado de líneas secantes y suma de puntos requiere de 11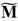 y 4
y 4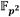 , mientras que en el cálculo de tangentes junto al doblado de puntos se utilizan 7
, mientras que en el cálculo de tangentes junto al doblado de puntos se utilizan 7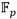 y 5
y 5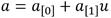 . Asimismo, para el cuadrado y la multiplicación dispersa en
. Asimismo, para el cuadrado y la multiplicación dispersa en 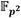 se tienen métricas de 12
se tienen métricas de 12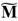 y 13
y 13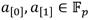 respectivamente (ver Algoritmo 5 y Algoritmo 6). Debido a que el valor
respectivamente (ver Algoritmo 5 y Algoritmo 6). Debido a que el valor 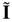 seleccionado en la Sección 2 conlleva a que la longitud del bucle de Miller
seleccionado en la Sección 2 conlleva a que la longitud del bucle de Miller 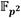 sea un número de 65 bits con un peso de Hamming de 5, en total se realizan 64 evaluaciones de tangentes y doblado de puntos, cuatro evaluaciones de líneas secantes y suma de puntos, así como 64 cuadrados y 68 multiplicaciones dispersas en
sea un número de 65 bits con un peso de Hamming de 5, en total se realizan 64 evaluaciones de tangentes y doblado de puntos, cuatro evaluaciones de líneas secantes y suma de puntos, así como 64 cuadrados y 68 multiplicaciones dispersas en 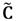 . Esto conduce a un costo de 2144
. Esto conduce a un costo de 2144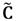 y 336
y 336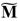 para el bucle de Miller. Realizando un análisis similar con la etapa de exponenciación final se puede obtener un costo estimado para la misma de 1780
para el bucle de Miller. Realizando un análisis similar con la etapa de exponenciación final se puede obtener un costo estimado para la misma de 1780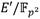 , 772
, 772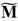 y 1
y 1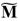 , lo cual suma un total de 3924
, lo cual suma un total de 3924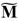 , 1108
, 1108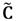 y 1
y 1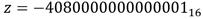 para el emparejamiento AteOpt-BN. Esto implica que, de las operaciones en
para el emparejamiento AteOpt-BN. Esto implica que, de las operaciones en 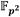 con mayor demanda computacional, la multiplicación ocupa aproximadamente el 78% de la carga de procesamiento. Es por ello que la formulación algorítmica adecuada y la implementación eficiente de esta operación resultan cruciales para incrementar el rendimiento del proceso de cálculo de un emparejamiento.
con mayor demanda computacional, la multiplicación ocupa aproximadamente el 78% de la carga de procesamiento. Es por ello que la formulación algorítmica adecuada y la implementación eficiente de esta operación resultan cruciales para incrementar el rendimiento del proceso de cálculo de un emparejamiento.
Teniendo en cuenta lo anterior, para implementar la multiplicación en 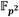 se ha optado por la técnica de multiplicación de binomios de Karatsuba [47] en combinación con la reducción módulo u2 + 1. De ahí se derivan las expresiones que se muestran en la ecuación (11) para calcular los coeficientes
se ha optado por la técnica de multiplicación de binomios de Karatsuba [47] en combinación con la reducción módulo u2 + 1. De ahí se derivan las expresiones que se muestran en la ecuación (11) para calcular los coeficientes 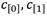 del elemento c = a · b [48]. En estas expresiones ya se tiene implícita la etapa de reducción considerando la equivalencia u2 = -1 (11).
del elemento c = a · b [48]. En estas expresiones ya se tiene implícita la etapa de reducción considerando la equivalencia u2 = -1 (11).
En la formulación de la secuencia algorítmica que materializa la ecuación (11) se ha tenido en cuenta, además, la posibilidad de aplicar la estrategia de reducción demorada [49] debido a que el módulo 𝑝 que se obtiene al evaluar la ecuación (1) para 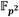 resulta en un número de exactamente 254 bits. Esta longitud queda dos bits por debajo de 256 que es el múltiplo más cercano del ancho de palabra de 64 bits seleccionado para las implementaciones realizadas en el contexto de esta investigación. Tal diferencia abre margen para que se puedan acumular varias operaciones de multiplicación y suma de enteros (elementos de
resulta en un número de exactamente 254 bits. Esta longitud queda dos bits por debajo de 256 que es el múltiplo más cercano del ancho de palabra de 64 bits seleccionado para las implementaciones realizadas en el contexto de esta investigación. Tal diferencia abre margen para que se puedan acumular varias operaciones de multiplicación y suma de enteros (elementos de 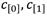 ) antes de tener que aplicar una reducción modular. Esto permite disminuir la cantidad de reducciones modulares e incrementar así el rendimiento general de una multiplicación en
) antes de tener que aplicar una reducción modular. Esto permite disminuir la cantidad de reducciones modulares e incrementar así el rendimiento general de una multiplicación en 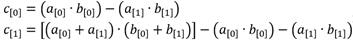 . El Algoritmo 4 muestra los pasos detallados del procedimiento resultante. Cabe señalar que todas las operaciones de suma, resta y multiplicación que forman parte del algoritmo corresponden a operaciones convencionales de la aritmética con números enteros, a la vez que es posible notar que las operaciones de reducción modular (sólo una por cada coeficiente calculado) han sido demoradas y se efectúan solamente al final del algoritmo.
. El Algoritmo 4 muestra los pasos detallados del procedimiento resultante. Cabe señalar que todas las operaciones de suma, resta y multiplicación que forman parte del algoritmo corresponden a operaciones convencionales de la aritmética con números enteros, a la vez que es posible notar que las operaciones de reducción modular (sólo una por cada coeficiente calculado) han sido demoradas y se efectúan solamente al final del algoritmo.
Como se ha mencionado anteriormente, las principales operaciones aritméticas en  involucradas en el bucle de Miller son el cuadrado y la multiplicación dispersa. Dados los elementos
involucradas en el bucle de Miller son el cuadrado y la multiplicación dispersa. Dados los elementos 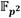 y
y  , donde
, donde 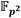 con
con 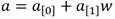 se formulan los siguientes algoritmos para implementar dichas operaciones:
se formulan los siguientes algoritmos para implementar dichas operaciones:
La definición de la torre de campos de la Sección 4 implica que la aritmética en  se nutre de operaciones en 𝔽 𝑝 6 que a su vez involucran operaciones aritméticas en
se nutre de operaciones en 𝔽 𝑝 6 que a su vez involucran operaciones aritméticas en 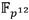 . Teniendo esto en cuenta, no es complicado expresar el costo del Algoritmo 5 en función de operaciones en
. Teniendo esto en cuenta, no es complicado expresar el costo del Algoritmo 5 en función de operaciones en  . Para la aritmética en
. Para la aritmética en 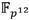 se emplearon las expresiones para extensiones cúbicas definidas en [48] donde se puede constatar que una multiplicación en
se emplearon las expresiones para extensiones cúbicas definidas en [48] donde se puede constatar que una multiplicación en 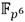 involucra seis multiplicaciones en
involucra seis multiplicaciones en 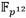 . Esto significa que para un cuadrado en
. Esto significa que para un cuadrado en 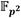 se requieren realizar doce multiplicaciones en
se requieren realizar doce multiplicaciones en 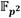 (pasos 1 y 6 del Algoritmo 5). Los pasos se refieren a multiplicaciones por la constante 𝛾 que solamente involucran sumas, restas y desplazamientos con elementos de
(pasos 1 y 6 del Algoritmo 5). Los pasos se refieren a multiplicaciones por la constante 𝛾 que solamente involucran sumas, restas y desplazamientos con elementos de 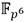 .
.
En el caso del Algoritmo 6 se puede observar que las operaciones se realizan sobre coeficientes en 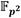 (ver notación definida en la Sección 4), con lo cual es simple notar que este algoritmo involucra un saldo de trece multiplicaciones en
(ver notación definida en la Sección 4), con lo cual es simple notar que este algoritmo involucra un saldo de trece multiplicaciones en  .
.
Coprocesador de multiplicación en 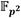
Tanto en el Algoritmo 2 como en el Algoritmo 3 las operaciones de multiplicación en  se han organizado cuidadosamente de manera que exista la mayor independencia de datos posible. Lo mismo sucede con el Algoritmo 6. Como regla general, aquellas multiplicaciones en
se han organizado cuidadosamente de manera que exista la mayor independencia de datos posible. Lo mismo sucede con el Algoritmo 6. Como regla general, aquellas multiplicaciones en  sin dependencia de datos han sido agrupadas y dispuestas de forma consecutiva en la formulación de cada uno de esos algoritmos. Por ejemplo, las dos multiplicaciones en
sin dependencia de datos han sido agrupadas y dispuestas de forma consecutiva en la formulación de cada uno de esos algoritmos. Por ejemplo, las dos multiplicaciones en 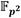 de los pasos 2 y 3 del Algoritmo 2 son independientes entre sí, así como las dos de los pasos 5 y 6, las tres de los pasos del 21 al 23 y el par de los pasos 26 y 27. Algo similar sucede en el Algoritmo 3, pero es en el Algoritmo 6 donde este paralelismo resulta más notable ya que las trece multiplicaciones en
de los pasos 2 y 3 del Algoritmo 2 son independientes entre sí, así como las dos de los pasos 5 y 6, las tres de los pasos del 21 al 23 y el par de los pasos 26 y 27. Algo similar sucede en el Algoritmo 3, pero es en el Algoritmo 6 donde este paralelismo resulta más notable ya que las trece multiplicaciones en 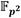 que aparecen en ese procedimiento son completamente independientes. Así, se genera la posibilidad, en cada caso, de agrupar las operaciones de multiplicación en
que aparecen en ese procedimiento son completamente independientes. Así, se genera la posibilidad, en cada caso, de agrupar las operaciones de multiplicación en 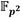 para ser ejecutadas de forma simultánea en tanto se disponga de la capacidad de procesamiento para ello. Esto ha sido aprovechado por los autores de [15] en una implementación software basada en procesamiento doble núcleo para acelerar el cálculo del emparejamiento AteOpt-BN agrupando y ejecutando en paralelo las operaciones de multiplicación en
para ser ejecutadas de forma simultánea en tanto se disponga de la capacidad de procesamiento para ello. Esto ha sido aprovechado por los autores de [15] en una implementación software basada en procesamiento doble núcleo para acelerar el cálculo del emparejamiento AteOpt-BN agrupando y ejecutando en paralelo las operaciones de multiplicación en 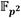 de dos en dos. De esta forma lograron obtener una mejora de rendimiento de un 20% respecto a una variante de solución desplegada en un solo núcleo. No obstante, en el análisis anterior se constata que los diferentes niveles de procesamiento aritmético de un emparejamiento admiten capacidades superiores de paralelismo.
de dos en dos. De esta forma lograron obtener una mejora de rendimiento de un 20% respecto a una variante de solución desplegada en un solo núcleo. No obstante, en el análisis anterior se constata que los diferentes niveles de procesamiento aritmético de un emparejamiento admiten capacidades superiores de paralelismo.
Precisamente, esta sección se propone explotar los recursos disponibles en las plataformas de hardware reconfigurable con el fin de implementar un coprocesador que acelere la operación de multiplicación en 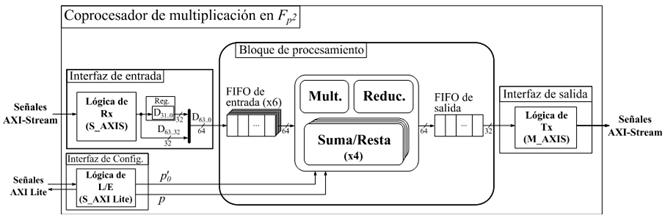 en el contexto de los emparejamientos bilineales. Con ello se persigue desarrollar una solución híbrida hardware⁄software donde las operaciones de alto nivel involucradas en el cálculo del emparejamiento se implementen en software en un microprocesador, el cual estaría en interacción con el coprocesador para efectuar las multiplicaciones en
en el contexto de los emparejamientos bilineales. Con ello se persigue desarrollar una solución híbrida hardware⁄software donde las operaciones de alto nivel involucradas en el cálculo del emparejamiento se implementen en software en un microprocesador, el cual estaría en interacción con el coprocesador para efectuar las multiplicaciones en 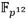 subyacentes y aprovechar así la posibilidad de simultanear la ejecución de varias de estas multiplicaciones.
subyacentes y aprovechar así la posibilidad de simultanear la ejecución de varias de estas multiplicaciones.
Para el despliegue de esta solución híbrida hardware⁄software fue empleada la placa de desarrollo ZedBoard [50] como plataforma de pruebas. Esta placa está basada en el dispositivo SoC-FPGA Zynq-7000 XC7Z020 de Xilinx, el cual integra en un mismo encapsulado un sistema de procesamiento basado en un microprocesador ARM Cortex-A9 de doble núcleo junto a un FPGA de la serie 7 de Xilinx [51].
Premisas de diseño
En esencia, el diseño del coprocesador de multiplicación en 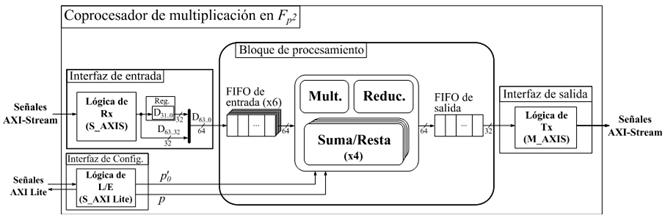 consiste en una traducción a hardware del Algoritmo 4, donde se han tenido en cuenta tres premisas fundamentales:
consiste en una traducción a hardware del Algoritmo 4, donde se han tenido en cuenta tres premisas fundamentales:
Aprovechar el paralelismo existente en las operaciones internas de una multiplicación en
 .
.Proporcionar el mayor grado de paralelismo posible al ejecutar simultáneamente varias operaciones de multiplicación en
 pero manteniendo un consumo moderado de recursos hardware.
pero manteniendo un consumo moderado de recursos hardware.Gestionar la comunicación entre el coprocesador y el microprocesador de forma eficiente.
La primera premisa se refiere a que las operaciones que conforman una multiplicación en 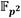 también exhiben cierto grado de paralelismo. Es fácil notar que las sumas y multiplicaciones de números enteros indicadas en los primeros cuatro pasos del Algoritmo 4 no presentan dependencia de datos. Lo mismo sucede con las reducciones modulares de los pasos 9 y 10. Esto evidentemente permite paralelizar el cálculo de dichas operaciones en la implementación del coprocesador.
también exhiben cierto grado de paralelismo. Es fácil notar que las sumas y multiplicaciones de números enteros indicadas en los primeros cuatro pasos del Algoritmo 4 no presentan dependencia de datos. Lo mismo sucede con las reducciones modulares de los pasos 9 y 10. Esto evidentemente permite paralelizar el cálculo de dichas operaciones en la implementación del coprocesador.
La segunda premisa expresa el objetivo principal del coprocesador, el cual, como se ha mencionado, consiste en ejecutar en paralelo varias operaciones de multiplicación en 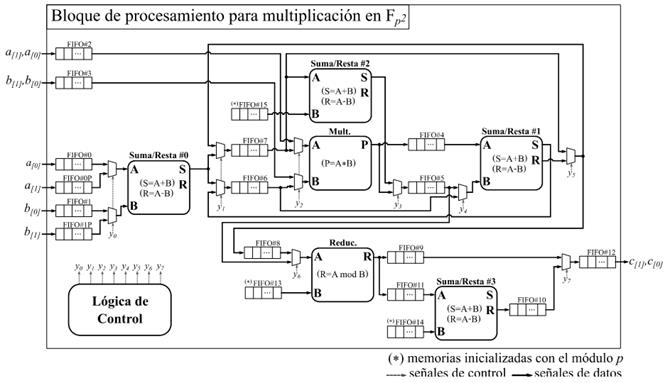 , lo cual se pudiera lograr replicando la arquitectura concebida para una multiplicación tantas veces como sea necesario. No obstante, este enfoque puede conducir a un consumo elevado de recursos hardware, lo cual, en algunos casos, puede resultar en un diseño irrealizable o con un balance poco factible entre costo y beneficio. Una alternativa que consigue minimizar el consumo de recursos consiste en diseñar una arquitectura que solape varias operaciones de multiplicación en
, lo cual se pudiera lograr replicando la arquitectura concebida para una multiplicación tantas veces como sea necesario. No obstante, este enfoque puede conducir a un consumo elevado de recursos hardware, lo cual, en algunos casos, puede resultar en un diseño irrealizable o con un balance poco factible entre costo y beneficio. Una alternativa que consigue minimizar el consumo de recursos consiste en diseñar una arquitectura que solape varias operaciones de multiplicación en  sobre un único bloque de procesamiento hardware. Para ello, se concibe una estructura de pipeline que, siguiendo el planteamiento de la primera premisa, organiza el flujo de ejecución de una multiplicación en
sobre un único bloque de procesamiento hardware. Para ello, se concibe una estructura de pipeline que, siguiendo el planteamiento de la primera premisa, organiza el flujo de ejecución de una multiplicación en  en varias etapas de procesamiento que actúan en paralelo. Cuando una etapa termina de procesar los datos de una operación le entrega los resultados parciales a la etapa siguiente y queda lista para procesar nuevos datos que lleguen a su entrada, los cuales corresponderán a una nueva operación. Esta cadena de procesamiento induce un efecto de paralelismo que logra reducir el tiempo necesario para obtener el resultado de cada nueva multiplicación en
en varias etapas de procesamiento que actúan en paralelo. Cuando una etapa termina de procesar los datos de una operación le entrega los resultados parciales a la etapa siguiente y queda lista para procesar nuevos datos que lleguen a su entrada, los cuales corresponderán a una nueva operación. Esta cadena de procesamiento induce un efecto de paralelismo que logra reducir el tiempo necesario para obtener el resultado de cada nueva multiplicación en  .
.
La última premisa refleja el hecho de que el rendimiento de una solución híbrida hardware/software no puede desligarse del mecanismo empleado para el intercambio de datos. La gestión eficiente de la comunicación entre el microprocesador y el coprocesador de multiplicación en 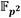 debe abordarse desde diferentes aristas. Por un lado, es importante seleccionar la interfaz de comunicación que mejor se ajuste a los requisitos de la solución en cuanto a la estructura y el volumen de los datos a transferir y, por el otro, es preciso enlazar este flujo de datos con la cadena de procesamiento de forma que no se afecte el proceso de ejecución de una multiplicación en
debe abordarse desde diferentes aristas. Por un lado, es importante seleccionar la interfaz de comunicación que mejor se ajuste a los requisitos de la solución en cuanto a la estructura y el volumen de los datos a transferir y, por el otro, es preciso enlazar este flujo de datos con la cadena de procesamiento de forma que no se afecte el proceso de ejecución de una multiplicación en 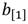 . En este sentido, téngase en cuenta que un elemento de
. En este sentido, téngase en cuenta que un elemento de 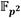 está compuesto por dos elementos de
está compuesto por dos elementos de 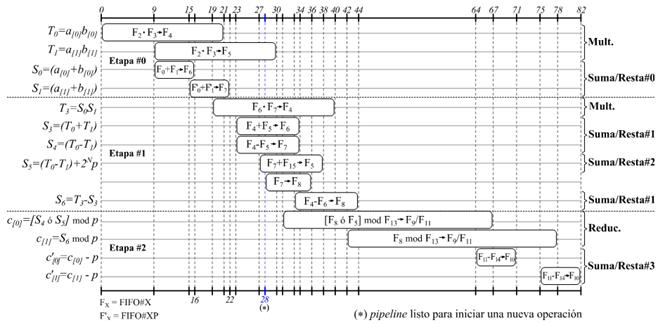 , los cuales, en el marco de esta investigación, corresponden a números enteros de longitud n = 254 representados como secuencias de
, los cuales, en el marco de esta investigación, corresponden a números enteros de longitud n = 254 representados como secuencias de 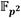 palabras de ω bits. En este caso para el microprocesador ARM de la plataforma Zynq-7000 se tiene que ω = 32. Por tanto, un elemento de
palabras de ω bits. En este caso para el microprocesador ARM de la plataforma Zynq-7000 se tiene que ω = 32. Por tanto, un elemento de 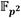 equivale a 16 palabras de 32 bits. Esto implica que por cada multiplicación en
equivale a 16 palabras de 32 bits. Esto implica que por cada multiplicación en 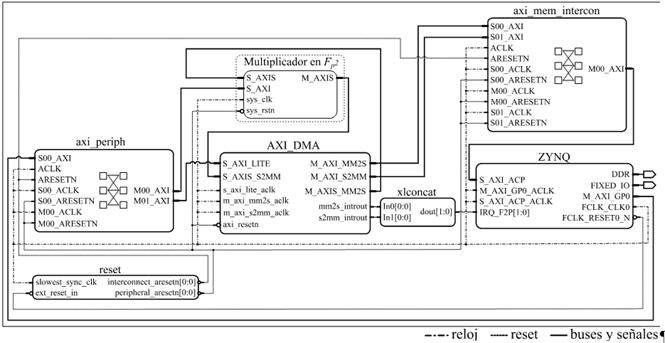 se deben transferir 48 palabras, 32 de ellas durante el envío de los operandos desde el microprocesador y otras 16 correspondientes al resultado devuelto por el coprocesador. Así, para la multiplicación dispersa en
se deben transferir 48 palabras, 32 de ellas durante el envío de los operandos desde el microprocesador y otras 16 correspondientes al resultado devuelto por el coprocesador. Así, para la multiplicación dispersa en 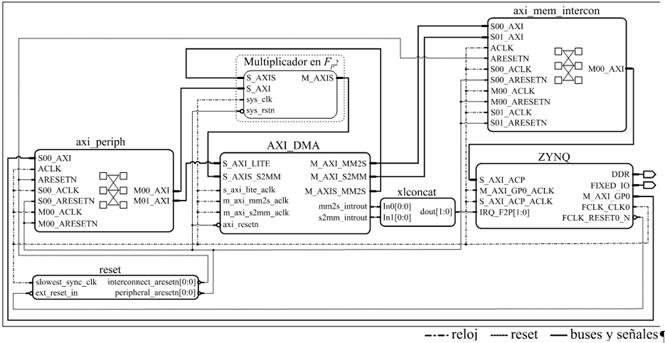 , que con trece operaciones simultáneas de multiplicación en
, que con trece operaciones simultáneas de multiplicación en 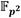 es la que impone el requisito más exigente, se deben realizar un total de 624 trasferencias de 32 bits entre el microprocesador y el coprocesador. La alternativa adecuada para gestionar este volumen de transferencias de manera eficiente en el contexto de la plataforma Zynq-7000 consiste en establecer enlaces punto-a-punto mediante interfaces AXI-Stream [52] de conjunto con la técnica de Acceso Directo a Memoria. Además, debido a que los operandos se organizan y transfieren formando secuencias de palabras, es oportuno que la estructura referida anteriormente para el procesamiento en forma de pipeline sea concebida para que sus diferentes etapas actúen también sobre palabras. De esta manera, a medida que lleguen al coprocesador las palabras de los operandos, se van introduciendo en la cadena de procesamiento, devolviéndose el resultado a partir de que se genere la primera palabra del mismo. Esto permite cierto grado de solapamiento entre la transferencia y el procesamiento de datos, lo cual contribuye a reducir el tiempo total de ejecución.
es la que impone el requisito más exigente, se deben realizar un total de 624 trasferencias de 32 bits entre el microprocesador y el coprocesador. La alternativa adecuada para gestionar este volumen de transferencias de manera eficiente en el contexto de la plataforma Zynq-7000 consiste en establecer enlaces punto-a-punto mediante interfaces AXI-Stream [52] de conjunto con la técnica de Acceso Directo a Memoria. Además, debido a que los operandos se organizan y transfieren formando secuencias de palabras, es oportuno que la estructura referida anteriormente para el procesamiento en forma de pipeline sea concebida para que sus diferentes etapas actúen también sobre palabras. De esta manera, a medida que lleguen al coprocesador las palabras de los operandos, se van introduciendo en la cadena de procesamiento, devolviéndose el resultado a partir de que se genere la primera palabra del mismo. Esto permite cierto grado de solapamiento entre la transferencia y el procesamiento de datos, lo cual contribuye a reducir el tiempo total de ejecución.
Arquitectura del coprocesador
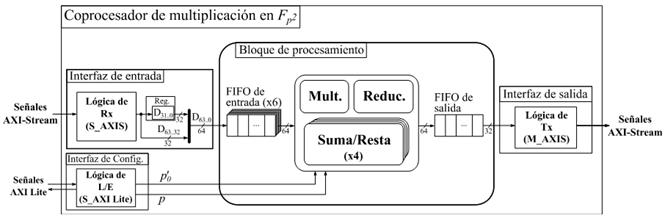
La Figura 1 muestra la estructura del coprocesador de multiplicación en 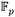 . Las interfaces de entrada y salida de datos corresponden a enlaces AXI-Stream de tipo esclavo y maestro respectivamente. Para la interfaz de configuración se emplea una interfaz esclava de bus AXI dedicada a la recepción de los parámetros de operación del coprocesador. El bloque de procesamiento contiene los aceleradores aritméticos correspondientes a las operaciones de suma, resta, multiplicación y reducción modular de números enteros de múltiple precisión que conforman la cadena de procesamiento de una multiplicación en
. Las interfaces de entrada y salida de datos corresponden a enlaces AXI-Stream de tipo esclavo y maestro respectivamente. Para la interfaz de configuración se emplea una interfaz esclava de bus AXI dedicada a la recepción de los parámetros de operación del coprocesador. El bloque de procesamiento contiene los aceleradores aritméticos correspondientes a las operaciones de suma, resta, multiplicación y reducción modular de números enteros de múltiple precisión que conforman la cadena de procesamiento de una multiplicación en 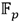 . Si bien los enlaces AXI-Stream de las interfaces de entrada y salida manipulan un ancho de datos de 32 bits, el mejor balance entre rendimiento y consumo hardware de los aceleradores aritméticos del bloque de procesamiento se obtuvo para un ancho de palabra de 64 bits. Por tal motivo, cada par de transferencias de 32 bits recibidas en la interfaz de entrada de datos se agrupan en palabras de 64 bits que son enviadas hacia la FIFO (First In-First Out) de entrada del bloque de procesamiento. Por otro lado, cada vez que se genera una nueva palabra del resultado, esta se escribe en la FIFO de salida, la cual ofrece una interfaz de datos de 64 bits hacia la lógica interna del bloque de procesamiento y otra de 32 bits hacia la interfaz de salida de datos. De esta manera el ajuste del ancho de palabra se produce de forma automática pues cada palabra escrita (64 bits) en la FIFO desencadena la lectura de dos palabras de 32 bits para ser transferidas mediante el enlace AXI-Stream de la interfaz de salida.
. Si bien los enlaces AXI-Stream de las interfaces de entrada y salida manipulan un ancho de datos de 32 bits, el mejor balance entre rendimiento y consumo hardware de los aceleradores aritméticos del bloque de procesamiento se obtuvo para un ancho de palabra de 64 bits. Por tal motivo, cada par de transferencias de 32 bits recibidas en la interfaz de entrada de datos se agrupan en palabras de 64 bits que son enviadas hacia la FIFO (First In-First Out) de entrada del bloque de procesamiento. Por otro lado, cada vez que se genera una nueva palabra del resultado, esta se escribe en la FIFO de salida, la cual ofrece una interfaz de datos de 64 bits hacia la lógica interna del bloque de procesamiento y otra de 32 bits hacia la interfaz de salida de datos. De esta manera el ajuste del ancho de palabra se produce de forma automática pues cada palabra escrita (64 bits) en la FIFO desencadena la lectura de dos palabras de 32 bits para ser transferidas mediante el enlace AXI-Stream de la interfaz de salida.
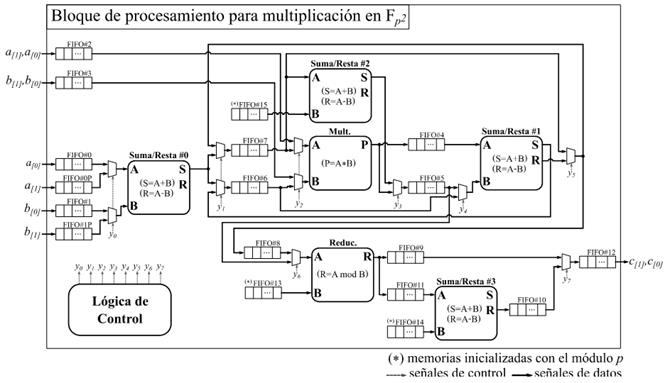
La arquitectura detallada del bloque de procesamiento se muestra en la Figura 2. Esta arquitectura constituye una variante de implementación hardware del Algoritmo 4 en la que se han tenido en cuenta las premisas de diseño referidas anteriormente. Como se puede apreciar, la cadena de procesamiento está integrada por cuatro módulos de suma y resta (Suma/Resta #0...#3), un módulo de multiplicación (Mult.) y otro de reducción modular (Reduc.). Además, se puede observar un conjunto de memorias de tipo FIFO distribuidas a lo largo de la cadena de procesamiento. Estas tienen como objetivo ir acumulando los datos de entrada de cada uno de los módulos funcionales para acoplar así las diferentes capacidades de procesamiento que estos poseen. De esta forma se evita que un módulo tenga que detener su funcionamiento en espera de que el siguiente se encuentre disponible para admitir nuevos datos de entrada. En particular, las memorias de la FIFO#0 a la FIFO#3, así como la FIFO#0P y la FIFO#1P, conforman el subsistema de almacenamiento de entrada del bloque de procesamiento donde se alojan los operandos recibidos mediante la interfaz de entrada del coprocesador. Por su parte, en la memoria FIFO#12 se van almacenando los resultados que son accedidos posteriormente por la interfaz de salida. Las conexiones detalladas tanto de las señales de reloj como de las señales de control de las memorias FIFO se han omitido para mantener la simplicidad del esquema. El módulo identificado como Lógica de Control representa la implementación de una máquina de estados finitos que se encarga de gestionar el proceso de ejecución y ajustar el flujo de datos de acuerdo a los requisitos de la cadena de procesamiento.
A medida que se reciben las palabras de los coeficientes 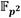 de los operandos
de los operandos 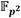 y
y 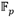 , estas se replican convenientemente en varias de las memorias FIFO del subsistema de entrada del bloque de procesamiento. Así, los coeficientes
, estas se replican convenientemente en varias de las memorias FIFO del subsistema de entrada del bloque de procesamiento. Así, los coeficientes 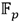 y
y 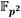 se almacenan en ese orden en la FIFO#2, pero también se guardan
se almacenan en ese orden en la FIFO#2, pero también se guardan 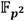 en la FIFO#0 y
en la FIFO#0 y 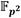 en la FIFO#0P. De forma análoga, los coeficientes
en la FIFO#0P. De forma análoga, los coeficientes 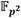 y
y 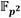 son alojados en ese orden en la FIFO#3. El coeficiente
son alojados en ese orden en la FIFO#3. El coeficiente 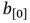 se almacena además en la FIFO#1, mientras que
se almacena además en la FIFO#1, mientras que 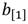 se guarda también en la FIFO#1P. Esto posibilita que dichos coeficientes puedan ser leídos de manera independiente por los módulos Suma/Resta #0 y Mult. para efectuar de forma concurrente en una primera etapa de procesamiento las operaciones involucradas en los pasos del 1 al 4 del Algoritmo 4. A medida que se obtienen los resultados intermedios de esta primera etapa, se activa una segunda fase de procesamiento en la que intervienen los módulos Mult., Suma/Resta #1 y Suma/Resta #2 para simultanear el cálculo de las operaciones indicadas en los pasos del 5 al 8. Finalmente, como parte de una tercera y última etapa de procesamiento, los módulos Reduc. y Suma/Resta #3 se encargan de efectuar las reducciones modulares de los pasos 9 y 10. Como resultado, estas tres etapas de procesamiento derivan en la conformación de una estructura de pipeline que satisface los propósitos de las dos primeras premisas de diseño definidas al inicio de este apartado.
se guarda también en la FIFO#1P. Esto posibilita que dichos coeficientes puedan ser leídos de manera independiente por los módulos Suma/Resta #0 y Mult. para efectuar de forma concurrente en una primera etapa de procesamiento las operaciones involucradas en los pasos del 1 al 4 del Algoritmo 4. A medida que se obtienen los resultados intermedios de esta primera etapa, se activa una segunda fase de procesamiento en la que intervienen los módulos Mult., Suma/Resta #1 y Suma/Resta #2 para simultanear el cálculo de las operaciones indicadas en los pasos del 5 al 8. Finalmente, como parte de una tercera y última etapa de procesamiento, los módulos Reduc. y Suma/Resta #3 se encargan de efectuar las reducciones modulares de los pasos 9 y 10. Como resultado, estas tres etapas de procesamiento derivan en la conformación de una estructura de pipeline que satisface los propósitos de las dos primeras premisas de diseño definidas al inicio de este apartado.
La Figura 3 muestra el flujo de datos detallado de la estructura de pipeline del coprocesador de multiplicación en 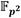 . De esta forma, se pueden observar la secuencia en que ocurren las diferentes operaciones, así como la cantidad de ciclos de reloj que se invierte en cada una de ellas.
. De esta forma, se pueden observar la secuencia en que ocurren las diferentes operaciones, así como la cantidad de ciclos de reloj que se invierte en cada una de ellas.
Como se puede apreciar, al inicio de cada línea se identifica la operación concreta de que se trata, mientras que dentro de la barra que representa su duración se muestra también la operación, pero indicando en este caso las memorias FIFO (Fi) que se utilizan como fuente y destino de datos. Además, al final de cada línea se puede observar qué módulo de aceleración aritmética se encuentra asociado a la ejecución de la operación. Aunque también se resaltan las tres etapas de procesamiento de la estructura de pipeline, nótese que los límites entre una y otra se encuentran solapados. Esto se debe a que los módulos aritméticos han sido implementados para operar palabra a palabra siguiendo su propio flujo interno de pipeline. Por tal motivo, basta que se encuentre lista la primera palabra del resultado de la última operación de una etapa para que se pueda iniciar la primera operación de la etapa de procesamiento siguiente. El hecho de que los módulos de aceleración aritmética cuenten con una estructura de pipeline interna también incide en la reducción del tiempo de ejecución de cada etapa y por ende del tiempo de ejecución total, lo cual ha permitido que el bloque de procesamiento invierta solamente 82 ciclos de reloj para ejecutar una multiplicación en 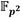 . Además, como se puede apreciar, a partir de los 28 ciclos ya es posible iniciar otra multiplicación. Así, mientras existan operandos en el subsistema de almacenamiento (memorias FIFO) de entrada, el bloque de procesamiento se mantiene ejecutando operaciones de multiplicación en
. Además, como se puede apreciar, a partir de los 28 ciclos ya es posible iniciar otra multiplicación. Así, mientras existan operandos en el subsistema de almacenamiento (memorias FIFO) de entrada, el bloque de procesamiento se mantiene ejecutando operaciones de multiplicación en 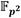 generando cada nuevo resultado en intervalos de 28 ciclos de reloj luego de que hayan transcurrido los 82 ciclos correspondientes a la primera multiplicación. Esto se traduce, por ejemplo, en que las trece multiplicaciones en
generando cada nuevo resultado en intervalos de 28 ciclos de reloj luego de que hayan transcurrido los 82 ciclos correspondientes a la primera multiplicación. Esto se traduce, por ejemplo, en que las trece multiplicaciones en 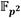 involucradas en una operación de multiplicación dispersa en
involucradas en una operación de multiplicación dispersa en 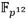 tarden unos 418 ciclos en ejecutarse. Esto representa aproximadamente un 60% de ahorro respecto a una variante que no explotase el pipeline.
tarden unos 418 ciclos en ejecutarse. Esto representa aproximadamente un 60% de ahorro respecto a una variante que no explotase el pipeline.
Discusión de resultados
La implementación del coprocesador de multiplicación en 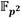 , así como la construcción del sistema de procesamiento híbrido hardware/software desplegado en el dispositivo Zynq-7000 XC7Z020 para el cálculo del emparejamiento AteOpt-BN fueron realizadas en el entorno de desarrollo Vivado Design Suite v2016.4. Para la descripción del coprocesador se utilizó el lenguaje VHDL (Very-High-Speed-Integrated-Circuit Hardware Description Language). Tras comprobar el correcto funcionamiento de cada uno de sus componentes, el coprocesador fue empaquetado como módulo IP (Intellectual Property) y añadido al sistema de procesamiento mostrado en la Figura 4. Como se puede apreciar la estructura del sistema se completa con el bloque ZYNQ, un controlador de acceso directo a memoria AXI_DMA, los componentes de interconexión axi_mem_intercon, axi_periph y xlconcat, así como el bloque de generación de reset.
, así como la construcción del sistema de procesamiento híbrido hardware/software desplegado en el dispositivo Zynq-7000 XC7Z020 para el cálculo del emparejamiento AteOpt-BN fueron realizadas en el entorno de desarrollo Vivado Design Suite v2016.4. Para la descripción del coprocesador se utilizó el lenguaje VHDL (Very-High-Speed-Integrated-Circuit Hardware Description Language). Tras comprobar el correcto funcionamiento de cada uno de sus componentes, el coprocesador fue empaquetado como módulo IP (Intellectual Property) y añadido al sistema de procesamiento mostrado en la Figura 4. Como se puede apreciar la estructura del sistema se completa con el bloque ZYNQ, un controlador de acceso directo a memoria AXI_DMA, los componentes de interconexión axi_mem_intercon, axi_periph y xlconcat, así como el bloque de generación de reset.
El bloque ZYNQ representa el sistema de procesamiento ARM Cortex-A9 presente en la familia de dispositivos SoC-FPGA Zynq-7000 al cual se le han habilitado su interfaz AXI de altas prestaciones (S_AXI_ACP) y las entradas de interrupción provenientes de la sección de lógica programable (IRQ_F2P). A la interfaz maestra M_AXI_GP0 se han acoplado las interfaces esclavas S_AXI y S_AXI_LITE del coprocesador de multiplicación en 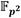 y el controlador AXI_DMA respectivamente. A través de estas el procesador ARM configura los parámetros de uno y otro componente. La frecuencia del procesador quedó configurada a 667 MHz mientras que para la lógica programable se utiliza un reloj de 100 MHz.
y el controlador AXI_DMA respectivamente. A través de estas el procesador ARM configura los parámetros de uno y otro componente. La frecuencia del procesador quedó configurada a 667 MHz mientras que para la lógica programable se utiliza un reloj de 100 MHz.

Figura 4 Sistema de procesamiento para la implementación híbrida hardware/software del emparejamiento AteOpt-BN utilizando el coprocesador de multiplicación en 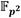 .
.
El controlador AXI_DMA fue configurado en modo simple. Las interfaces maestras de bus AXI de los canales de lectura (M_AXI_MM2S) y escritura (M_AXI_S2MM) del controlador de DMA han sido acopladas a la interfaz S_AXI_ACP del bloque ZYNQ para garantizar el acceso hacia el subsistema de memoria del procesador ARM. Las interfaces AXI-Stream M_AXIS_MM2S y S_AXIS_S2MM se conectan directamente a los bloques de entrada y salida de datos del coprocesador. El canal de lectura en memoria del controlador AXI_DMA fue configurado para realizar ráfagas de hasta 256 transferencias de 32 bits, valor máximo admitido [53]. Esto permite transferir ininterrumpidamente hasta 16 elementos de 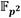 (operandos de ocho multiplicaciones) desde el procesador ARM hacia el coprocesador. En cambio, el canal de escritura en memoria quedó configurado para realizar ráfagas de 8 transferencias de 32 bits como máximo, lo cual coincide con el tamaño de un elemento en
(operandos de ocho multiplicaciones) desde el procesador ARM hacia el coprocesador. En cambio, el canal de escritura en memoria quedó configurado para realizar ráfagas de 8 transferencias de 32 bits como máximo, lo cual coincide con el tamaño de un elemento en 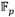 . De esta forma, independientemente del total de multiplicaciones a realizar, a partir de que el controlador AXI_DMA reciba el primer coeficiente en
. De esta forma, independientemente del total de multiplicaciones a realizar, a partir de que el controlador AXI_DMA reciba el primer coeficiente en 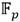 correspondiente al primer resultado de una multiplicación en
correspondiente al primer resultado de una multiplicación en 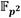 se comenzarán a escribir estos coeficientes en memoria. Así, al solaparse el flujo de datos desde el coprocesador hacia el controlador AXI_DMA con el envío de los mismos desde el controlador AXI_DMA hacia la memoria del procesador ARM, se obtiene un impacto positivo en el rendimiento del mecanismo de transferencias.
se comenzarán a escribir estos coeficientes en memoria. Así, al solaparse el flujo de datos desde el coprocesador hacia el controlador AXI_DMA con el envío de los mismos desde el controlador AXI_DMA hacia la memoria del procesador ARM, se obtiene un impacto positivo en el rendimiento del mecanismo de transferencias.
Los resultados de implementación del coprocesador de multiplicación en 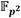 exhiben porcentajes de utilización en el dispositivo Zynq XC7Z020 de un 24% (3186) de slices, un 5% (7) de bloques dedicados de RAM y un 76% (168) de bloques DSP, siendo este último el elemento crítico del diseño en cuanto a consumo de recursos hardware. Este volumen de ocupación de bloques DSP está asociado a la implementación de las estructuras de pipeline de los módulos de multiplicación y reducción modular de números enteros. Para obtener el mayor rendimiento posible, se utilizan en cada caso cuatro unidades de procesamiento que operan en paralelo. Cada una de estas unidades emplean 16 bloques DSP en el caso de la multiplicación y 26 bloques DSP en el caso de la reducción modular, lo cual conduce al elevado consumo de este tipo de recurso. De no haber implementado estos módulos en base a estructuras de pipeline, la utilización de bloques DSP del coprocesador se reduciría a tan sólo 42. No obstante, el flujo de procesamiento mostrado en la Figura 3 sería impactado desfavorablemente ya que las operaciones de multiplicación y reducción modular no pudieran ocurrir de forma solapada. Esto implicaría que una multiplicación en
exhiben porcentajes de utilización en el dispositivo Zynq XC7Z020 de un 24% (3186) de slices, un 5% (7) de bloques dedicados de RAM y un 76% (168) de bloques DSP, siendo este último el elemento crítico del diseño en cuanto a consumo de recursos hardware. Este volumen de ocupación de bloques DSP está asociado a la implementación de las estructuras de pipeline de los módulos de multiplicación y reducción modular de números enteros. Para obtener el mayor rendimiento posible, se utilizan en cada caso cuatro unidades de procesamiento que operan en paralelo. Cada una de estas unidades emplean 16 bloques DSP en el caso de la multiplicación y 26 bloques DSP en el caso de la reducción modular, lo cual conduce al elevado consumo de este tipo de recurso. De no haber implementado estos módulos en base a estructuras de pipeline, la utilización de bloques DSP del coprocesador se reduciría a tan sólo 42. No obstante, el flujo de procesamiento mostrado en la Figura 3 sería impactado desfavorablemente ya que las operaciones de multiplicación y reducción modular no pudieran ocurrir de forma solapada. Esto implicaría que una multiplicación en 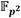 tardaría alrededor de 130 ciclos de reloj, retrasándose la posibilidad de iniciar cada nueva operación hasta 63 ciclos después de iniciada la anterior. En tal caso, por ejemplo, para ejecutar las trece multiplicaciones en
tardaría alrededor de 130 ciclos de reloj, retrasándose la posibilidad de iniciar cada nueva operación hasta 63 ciclos después de iniciada la anterior. En tal caso, por ejemplo, para ejecutar las trece multiplicaciones en 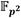 requeridas en una multiplicación dispersa en
requeridas en una multiplicación dispersa en 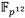 , se invertirían unos 886 ciclos de reloj, lo que representa un 52.8% más que los 418 ciclos que invierte la propuesta de solución basada en estructuras de pipeline.
, se invertirían unos 886 ciclos de reloj, lo que representa un 52.8% más que los 418 ciclos que invierte la propuesta de solución basada en estructuras de pipeline.
La parte software del diseño fue desarrollada en la herramienta Xilinx SDK v2016.4. Para la interacción con el coprocesador se implementaron seis funciones (cpDualFp2Mult, cpThreeFp2Mult, cpQuadFp2Mult, cpFifthFp2Mult, cpSixthFp2Mult y cpThirteenthFp2Mult) encargadas de la ejecución en ráfaga de dos, tres, cuatro, cinco, seis y trece multiplicaciones en cada caso. Estas funciones han sido empleadas en los diferentes niveles de procesamiento aritmético que requieren realizar operaciones de multiplicación en 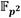 para completar el cálculo de un emparejamiento.
para completar el cálculo de un emparejamiento.
Para evaluar el desempeño del coprocesador primero se estudió el rendimiento de cada de las funciones anteriores. A partir de medir el tiempo de ejecución de 10000 repeticiones independientes de cada una de ellas, se calcularon los ciclos de reloj promedio que tardan en ejecutarse. Esto incluye el tiempo que se invierte en transferencias de datos entre el procesador ARM y el coprocesador. Los resultados correspondientes se pueden observar en la Tabla 1, los cuales, como referencia, se contrastan con los tiempos calculados en cada caso para una cantidad equivalente de multiplicaciones partiendo de las métricas presentadas en [15] para dos multiplicaciones en 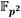 simultáneas utilizando procesamiento doble núcleo. Como se puede apreciar, los incrementos de rendimiento al utilizar el coprocesador implementado en este trabajo respecto a la solución software basada en procesamiento doble núcleo de [15] van desde un 19% para dos multiplicaciones hasta un 55.8% para el caso de trece multiplicaciones.
simultáneas utilizando procesamiento doble núcleo. Como se puede apreciar, los incrementos de rendimiento al utilizar el coprocesador implementado en este trabajo respecto a la solución software basada en procesamiento doble núcleo de [15] van desde un 19% para dos multiplicaciones hasta un 55.8% para el caso de trece multiplicaciones.
Tabla 1 Tiempos de ejecución de las funciones de multiplicación en 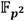 con el coprocesador
con el coprocesador
| Cantidad de multiplicaciones en |
Tiempos de ejecución (103 ciclos de reloj)† | |
|---|---|---|
| Procesamiento doble núcleo [15] | Coprocesador (este trabajo) | |
| 2 | 2.47 | 2.38 |
| 3 | 4.17 | 2.79 |
| 4 | 4.94 | 3.16 |
| 5 | 6.64 | 3.54 |
| 6 | 7.41 | 3.96 |
| 13 | 16.5 | 7.29 |
| † Los ciclos de reloj se expresan en base a la señal de reloj de 667 MHz del procesador ARM. | ||
La Tabla 2 muestra el impacto favorable que tiene el empleo del coprocesador de multiplicación en 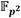 en una implementación híbrida hardware/software para incrementar el rendimiento del emparejamiento AteOpt-BN. Los tiempos para el bucle de Miller, la etapa de exponenciación final y por ende el tiempo total de ejecución del emparejamiento exhiben mejoras significativas en la solución propuesta en este trabajo en comparación con los valores obtenidos en [15] para la implementación basada en procesamiento doble núcleo. De igual modo se evidencia una mejora notable respecto a la solución híbrida hardware/software reportada en [20], única solución previa de este tipo identificada en el estado del arte para la implementación de emparejamientos bilineales. Concretamente, se han logrado mejoras en el tiempo de cálculo del emparejamiento AteOpt-BN de un 32% respecto a la solución de procesamiento doble núcleo de [15] y de un 22.5% en comparación con los resultados de la implementación híbrida de [20].
en una implementación híbrida hardware/software para incrementar el rendimiento del emparejamiento AteOpt-BN. Los tiempos para el bucle de Miller, la etapa de exponenciación final y por ende el tiempo total de ejecución del emparejamiento exhiben mejoras significativas en la solución propuesta en este trabajo en comparación con los valores obtenidos en [15] para la implementación basada en procesamiento doble núcleo. De igual modo se evidencia una mejora notable respecto a la solución híbrida hardware/software reportada en [20], única solución previa de este tipo identificada en el estado del arte para la implementación de emparejamientos bilineales. Concretamente, se han logrado mejoras en el tiempo de cálculo del emparejamiento AteOpt-BN de un 32% respecto a la solución de procesamiento doble núcleo de [15] y de un 22.5% en comparación con los resultados de la implementación híbrida de [20].
Aunque en [20] los autores también incluyen soporte hardware para las operaciones de suma, resta y cuadrado en 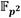 , su solución emplea una arquitectura con ancho de palabra de 32 bits. Incluso, en el caso de la multiplicación y el cuadrado, las operaciones básicas se realizan a partir de una unidad de multiplicación y acumulación de 32 x 16 bits. Esto contrasta con la arquitectura del coprocesador propuesto en este trabajo donde las unidades de procesamiento subyacentes emplean un ancho de palabra de 64 bits. Esto conduce a una reducción de la cantidad de ciclos de reloj que se requieren para completar cada operación, lo cual se traduce en un mejor rendimiento del proceso de cálculo de un emparejamiento en cuanto a tiempo de ejecución.
, su solución emplea una arquitectura con ancho de palabra de 32 bits. Incluso, en el caso de la multiplicación y el cuadrado, las operaciones básicas se realizan a partir de una unidad de multiplicación y acumulación de 32 x 16 bits. Esto contrasta con la arquitectura del coprocesador propuesto en este trabajo donde las unidades de procesamiento subyacentes emplean un ancho de palabra de 64 bits. Esto conduce a una reducción de la cantidad de ciclos de reloj que se requieren para completar cada operación, lo cual se traduce en un mejor rendimiento del proceso de cálculo de un emparejamiento en cuanto a tiempo de ejecución.
Tabla 2 Comparación de los tiempos de ejecución del emparejamiento AteOpt-BN
| Implementación | Tiempos de ejecución (103 ciclos de reloj) | ||
|---|---|---|---|
| Bucle de Miller | Exponenciación final | AteOpt-BN | |
| Procesamiento doble núcleo [15] | 4375 | 4456 | 8849 |
| Híbrida hardware/software [20] | - | - | 7763 |
| Híbrida hardware/software (este trabajo) | 2917 | 3085 | 6017 |
Conclusiones
Las operaciones aritméticas involucradas en el cálculo de un emparejamiento bilineal exhiben un alto grado de paralelismo. Debido a ello, resulta imprescindible explotar aquellas características tecnológicas de las plataformas de implementación que permitan aprovechar este paralelismo en pos de obtener implementaciones eficientes. En este sentido, el presente trabajo ha abordado la implementación de un coprocesador hardware para acelerar las operaciones de multiplicación en 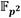 , por ser las de mayor incidencia en el cálculo de un emparejamiento. La arquitectura propuesta explota el uso de estructuras de pipeline en varios niveles, lo cual hace posible acelerar una multiplicación en sí y además simultanear el cálculo de varias operaciones de multiplicación. El impacto favorable de emplear este coprocesador se ha comprobado en una implementación híbrida hardware/software sobre un SoC-FPGA Zynq-7000 del emparejamiento Ate óptimo en curvas de Barreto-Naehrig que logra mejorar los resultados de trabajos previos que emplean estrategias de aceleración similares. Por otra parte, si bien se ha tomado como ejemplo el emparejamiento AteOpt-BN, el hecho de que las operaciones de alto nivel se implementen en software le otorga un nivel de flexibilidad a la solución propuesta que permite extrapolar los resultados obtenidos en este trabajo a la implementación de otros tipos de emparejamientos al aprovechar el paralelismo y la aceleración hardware que proporciona el coprocesador de multiplicación en
, por ser las de mayor incidencia en el cálculo de un emparejamiento. La arquitectura propuesta explota el uso de estructuras de pipeline en varios niveles, lo cual hace posible acelerar una multiplicación en sí y además simultanear el cálculo de varias operaciones de multiplicación. El impacto favorable de emplear este coprocesador se ha comprobado en una implementación híbrida hardware/software sobre un SoC-FPGA Zynq-7000 del emparejamiento Ate óptimo en curvas de Barreto-Naehrig que logra mejorar los resultados de trabajos previos que emplean estrategias de aceleración similares. Por otra parte, si bien se ha tomado como ejemplo el emparejamiento AteOpt-BN, el hecho de que las operaciones de alto nivel se implementen en software le otorga un nivel de flexibilidad a la solución propuesta que permite extrapolar los resultados obtenidos en este trabajo a la implementación de otros tipos de emparejamientos al aprovechar el paralelismo y la aceleración hardware que proporciona el coprocesador de multiplicación en  .
.