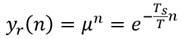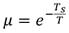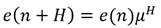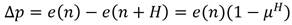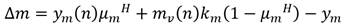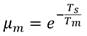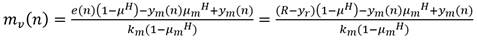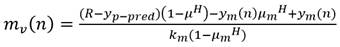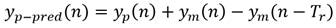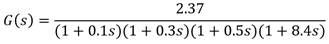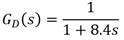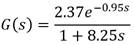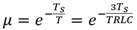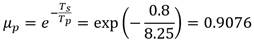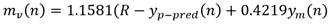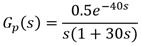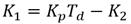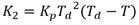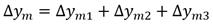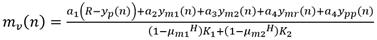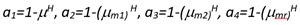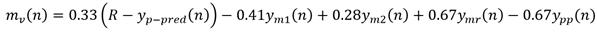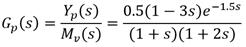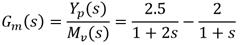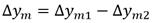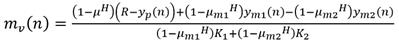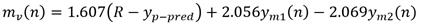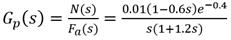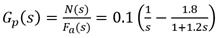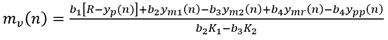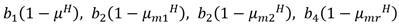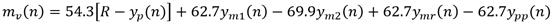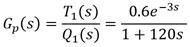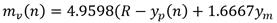Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
La década de 1960 fue testigo de muchos cambios en las actividades sociales, económicas y tecnológicas. En la teoría de los sistemas de control se producía un cambio de paradigma, y el enfoque del espacio de estados, el control óptimo y el filtro de Kalman son solo tres conceptos que surgieron en esa época y que han tenido un impacto duradero en el desarrollo posterior del análisis de sistemas y diseño de sistemas de control.
La tecnología de los sistemas de control industrial también estaba cambiando, respondiendo a las demandas industriales de un mejor rendimiento de los sistemas de complejidad creciente. Se estaba explorando el potencial de los sistemas de control digital directo y el control de procesos por computadora para proporcionar un mejor control coordinado y mejoras en el control de procesos y la calidad del producto.
Las industrias petroquímicas, siderúrgica y de servicios públicos, estuvieron entre las primeras industrias en utilizar y explotar estas nuevas capacidades. Motivado por las necesidades de la industria petroquímica y similar, a finales de la década de los 70 en los Estados Unidos de América comenzaron a desarrollar lo que se llamó inicialmente “un algoritmo computacional para el control de proceso multivariables”.
Los primeros resultados fueron presentados por los autores en un congreso de la AIChE y a partir de entonces comenzó denominarse al algoritmo como Control por Matriz Dinámica (DMC en inglés) [1]. Casi simultáneamente en Francia J. Richalet crea su primera versión de Control Predictivo a lo que se llamó Control basado en el Algoritmo del Modelo (MAC en inglés). Numerosas son las variantes de algoritmos y estructuras de MPC desarrolladas en el mundo y alto ha sido el auge de su aplicación a la industria y a otros procesos. A finales de los 70 Richalet ya formulaba las ideas básicas para el desarrollo de su algoritmo de Control Funcional Predictivo (PFC en inglés) y durante la siguiente década comenzaron las primeras aplicaciones industriales de su nuevo método. Una década de práctica industrial con PFC fue reportada en la literatura de archivo por su autor a inicio de los 80 [2]. A Jacques Richalet se le considera como el "abuelo" del MPC [3]. En general, al Control Predictivo se le asigna la capacidad de resolver problemas de control que presentan cierta dificultad (procesos con múltiples variables que interactúan, retardos, dinámica compleja, restricciones, etc.) en los que los algoritmos de control clásicos no alcanzan a obtener la calidad exigida. Las aplicaciones tienden a crecer debido a una serie de factores como son, el desarrollo actual de la tecnología digital para su implementación, exigencias crecientes de calidad, ahorro de energía, seguridad, flexibilidad en la producción, necesidad de integrar decisiones económicas y sistemas de control, diseño integrado de plantas y sistemas de control [4, 5].
Una motivación clave para el estudio es la de proporcionar un rendimiento comparable con el del controlador PID de uso generalizado, sin los inconvenientes indeseables que presenta la acción de control en los transitorios y al mismo tiempo verificar la posibilidad de su implementación práctica en sistemas empotrados, apoyado en el desarrollo de la tecnología digital moderna, tanto en hardware como en software. El PFC resulta así un algoritmo de control, muy simple de sintonizar, con un desempeño muy robusto en el control de los procesos con dinámicas complejas, seleccionable y fácilmente aplicable por los ingenieros de instrumentación y control de procesos [6]. Además, independientemente del auge alcanzado, no existía una metodología explícitamente organizada para el diseño e implementación de esta estructura de control de procesos, ni siquiera en laboratorios de bolsillo que facilitasen su enseñanza. De ahí que esa sea la problemática esencial tratada en el artículo, teniendo como objetivos principales presentar una metodología para el diseño del PFC básico y resaltar, en casos de estudio típicos, las posibilidades que brinda el mismo como estrategia alternativa para control de procesos con dinámicas complejas.
El resto del artículo se estructura de forma tal que en la sección 2 se elabora la metodología general de diseño del controlador PFC, en la sección 3 se presenta los resultados del análisis al aplicar la metodología a varios casos de estudio mediante simulación y prácticamente mediante pruebas reales en un mini-laboratorio de control de temperatura, cerrándose el articulo en la sección 4 donde se expresan las conclusiones de la investigación realizada.
Metodología
El método aplicado consiste en el desarrollo del procedimiento de diseño y análisis, primeramente mediante simulación de los resultados alcanzados en la aplicación del PFC a varios casos de estudio de control de procesos y finalmente la aplicación del sistema al control real de temperatura de un proceso a nivel de laboratorio.
Fundamentos del Control Predictivo Funcional. Procedimiento de síntesis
Los precursores del PFC sustentan el algoritmo en la genial idea de considerar que la trayectoria de referencia sea una exponencial decreciente con cierto factor de decremento μ, el cual se convierte en un parámetro de sintonía, de manera tal que en el tiempo discreto n, la señal de referencia y r siga la siguiente ley exponencial (1):
(1)
Evidentemente se toma (2):
(2)
Donde T s es el periodo de muestreo y T es la constante de tiempo predominante del proceso de orden reducido [7].
Se procura el incremento de la señal de salida Δp en un instante (n+H). Donde H representa un único instante del intervalo (H 1 , H 2 ) en que coinciden la trayectoria de salida y p del proceso y la referencia y r .
Si se representa por R el valor final deseado de consigna o referencia constante, el error con la trayectoria de referencia exponencial es como sigue (3):
(3)
El valor predicho en el instante (n+H) será (4):
(4)
La variación Δp que experimenta la señal de la salida del proceso en el intervalo (n, H) es (5):
(5)
De manera similar se verifica que, en el caso de procesos de primer orden sin retardo, considerando la respuesta de un modelo independiente de la salida del proceso y tomando su respuesta como la superposición de la respuesta libre más la forzada ante la señal de control, el decremento exponencial de la salida del modelo estaría dada por (6):
(6)
Donde (7):
(7)
Este es un aspecto importantísimo en el desarrollo de la metodología. En este caso y m es la señal de salida del modelo, m v es la señal de control (salida del PFC), k m es la ganancia del modelo de primer orden y T m su constante de tiempo. El cálculo de la señal de control m v se basa en el precepto creado por el Doctor Richalet de que, en un instante H del horizonte de coincidencia (H 1 , H 2 ), la variación (p de la salida del proceso predicha coincida con la variación de la señal del modelo (m, o sea: (p = (m. Así igualando ambos resultados dados en (5) y (6) resulta:
(8)
Puesto que la esencia del algoritmo es procurar que la salida del proceso y p siga la referencia y r , cuando en la planta exista retardo puro de transportación, digamos T r , en lugar de y r en el cálculo del error se utiliza el valor predicho de la variable del proceso y p-pred . (9)
(9)
Como se puede apreciar, el fundamento del método consiste en que, mediante la predicción de la salida del proceso y la evolución del modelo es posible encontrar el valor de la variable manipulada. El núcleo del método consiste en calcular la respuesta forzada del sistema para el vector de valores futuro de la variable controlada. En el PFC general, el cálculo de la solución se basa en estructurar la variable manipulada como la sumatoria de funciones base (U B0 escalón, U B1 rampa,…) de ahí el nombre de funcional que se le da al algoritmo por su autor, y calcular respuestas forzadas ante las mismas (Y B0 , Y B1 ,…). De esta manera se obtiene una matriz constante que permite calcular la respuesta forzada durante todo el control. El controlador se limita a encontrar los valores de la variable manipulada (m v ).
Valor predicho de la señal de salida del proceso retardado
El valor predicho de la señal permite realimentar al controlador PFC el valor real de la señal de salida del proceso para ello se utiliza el siguiente predictor (10):
(10)
El resultado indicado en (9) es válido para un sistema de primer orden sin retardo, sin embargo su extensión a cualquier sistema lineal retardado de orden superior es posible, mientras que se aproxime el modelo por uno de primer orden con retardo (POR) y se utilice (10) como predictor. En este caso el PFC se comporta de manera simular a una estructura de control por modelo interno con el compensador del retardo incluido.
Resultados y discusion
Se presentan a continuación cinco casos de estudio.
Caso de estudio 1: Control Predictivo Funcional de un intercambiador de calor vapor-agua encamisado sin retardo
Para cierto intercambiador de calor vapor-líquido, del tipo encamisado la función transferencial del lazo sin incluir el controlador es la siguiente:
El disturbio en la carga, considerado en la temperatura del líquido de entrada al intercambiador, actúa a través de la función transferencial siguiente:
Se desea controlar el proceso mediante un PFC para lo cual se procede a la síntesis del mismo según la metodología dada en el epígrafe anterior. En primer lugar se precisa reducir el modelo de cuarto orden a un modelo POR equivalente. Así se tiene:
Los parámetros del controlador PFC se calculan como sigue:
En primer lugar, se calcula el parámetro μ en base al criterio de que el tiempo de respuesta sea el requerido para que la señal de salida entre en una banda de toleración de ±5%. Para un primer orden, cuando ello ocurre el tiempo respuesta en lazo cerrado es aproximadamente igual a tres veces la contante de tiempo del proceso a lazo abierto. Este criterio se acepta normalmente en control de procesos y es ratificado por los precursores del PFC [8]. De manera que:
Donde TRLC es el tiempo de respuesta en lazo cerrado deseada. Tomando el periodo T s = 0.8 min y TRLC = 5.75 min resulta μ = 0.6588.
En sentido general H puede tomar cualquier valor entero de instantes de muestreo, en este caso se toma H=1. Además:
Para el proceso: La ganancia K p = 2.37, constante de tiempo T p = 8.25 min. El retardo en términos del periodo de muestro es n p = 1 (entero contenido entre T s /T r ). El decremento exponencial para el proceso es:
Para el modelo: Se considera que se adecua perfectamente al proceso, aunque podría no ser este el caso, con ganancia K m = 2.37, constante de tiempo T m = 8.25 min, retardo n m = 0. Factor de decremento del modelo μ m = μ p = 0.9076, de manera que según (9) la variable de salida del PFC está dada por la siguiente ecuación:
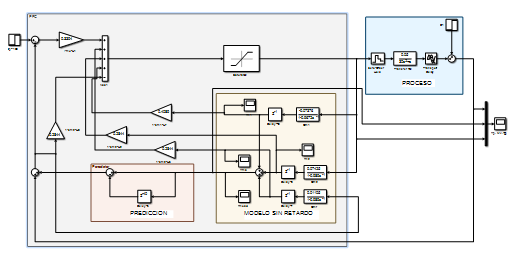
La simulación del sistema de control incluyendo restricciones en el mando para el PFC se muestra a continuación. (Figura 1):
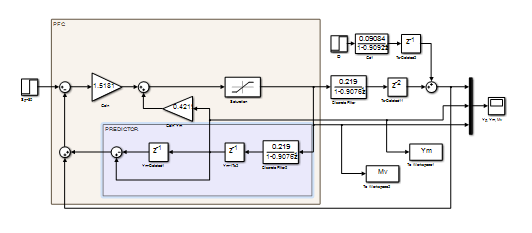(Elaboración propia)Figura 1 Simulación del FPC ante una R= 80 °C y un disturbio de entrada de 10°C al cabo de 20 minutos. Se incluyen restricciones en el mando solamente.
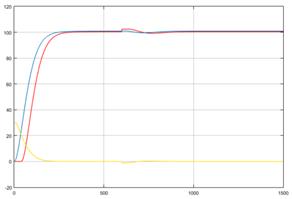
La respuesta en la temperatura de salida, la señal de salida del modelo y la variable de mando se muestran a continuación. (Figura 2)
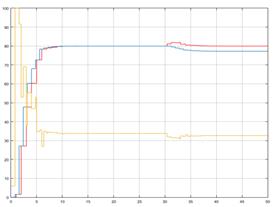(Elaboración propia)Figura 2 Temperatura de salida y p (rojo), señal del modelo y m (azul) y señal de mando m v (amarillo).
Obsérvese lo impecable de la respuesta sin la necesidad de efecto integral ni derivativo alguno.
Caso de estudio 2: Control Predictivo Funcional de un proceso inestable a lazo abierto con retardo
Sea el proceso de nivel de líquido en un tanque cuya función transferencial del lazo es la siguiente:
En este caso los precursores del PFC [9] postulan, como descomponer el modelo de la acción integradora en un conjunto de modelos de primer orden estables a lazo abierto. A partir de tales premisas se demuestra por los autores [10] que el modelo del proceso anterior es equivalente al que se muestra en la Fig. 3.
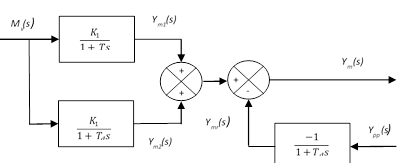(Richalet, J. y O´Donovan, D. (2009), pag. 45)Figura 3 Descomposición del modelo mediante la superposición de tres modelos lineales estables
Donde T es la constante de tiempo del proceso y T d es la llamada constante de descomposición del modelo y los criterios para su elección se ofrecen también por los autores. No obstante T d se elige de manera que esté en el intervalo TRLC que se toma como criterio de diseño [11]. Se demuestra que (11) y (12):
(11)
(12)
Evidentemente en este caso resulta (13):
(13)
Se aplica la metodología y el resulta para el mando m v la siguiente expression (14):
(14)
Donde (15):
(15)
Considerando en este caso particular T s = 1 s, T d = 90 s, H =100, aplicando (14) y (15) y siguiendo el mismo procedimiento del caso estudio 1, se obtiene para la señal de mando la siguiente expresión:
Se simula el sistema con una referencia R=100 cm y un disturbio tipo paso de amplitud 20% a los 600 segundos como se muestra en la Fig. 4.
La respuesta se muestra a continuación. (Figura 5)
Se observa el valor de estado estable sin sobrecresta y con el tiempo de establecimiento estipulado por diseño. Si el proceso resultara de orden superior al segundo, el primer paso del procedimiento seria llevarlo a un modelo POR equivalente con integración pura incluida.
Caso de estudio 3: Control Predictivo Funcional de un proceso con respuesta inversa (RI) y retardo
Sea el proceso en cierto rector continuo de tanque agitado donde la función transferencial entre la concentración de reactivo en la mezcla reaccionante y la entrada al elemento final del control es descrita por la siguiente expresión:
El tiempo se expresa en minutos. La RI inversa es evidente debido a la presencia del cero a la derecha del eje jω del plano s. El modelo del proceso, sin retardo, se puede expresar de la forma siguiente
De modo que (16):
(16)
Teniendo en cuenta (16) y aplicando la misma metodología como en el primer caso se llega a la siguiente expresión para la señal de control:
(17)
Se toma un periodo de muestreo T s = 1 min, el tiempo de establecimiento TRLC = 200 min y H se escoge igual a 100. Sustituyendo valores se tiene:
El esquema de simulación en simulink se muestra a continuación (Figura 6):
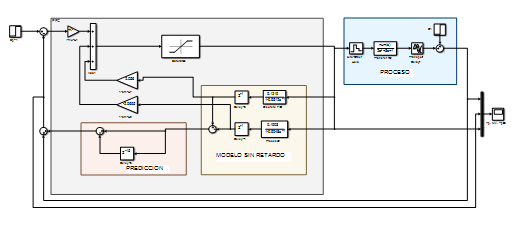(Elaboración propia)Figura 6 Simulación del PFC para un proceso con RI, con referencia R=1 y disturbio tipo paso de amplitud 0.1 en el instante t = 40 min.
Los resultados en la respuesta se muestran a continuación (Figura 7):
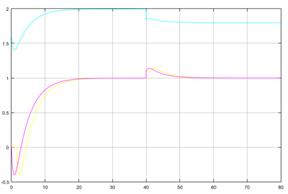(Elaboración propia)Figura 7 Respuesta del control PFC, y p (amarillo), y p-pred (rojo) y m v (verde).
El desempeño es totalmente satisfactorio.
Caso de estudio 4: Control Predictivo Funcional para el nivel del agua en el domo de un generador de vapor
Tratase de la síntesis de un PFC para la alimentación de agua al domo de una caldera industrial para regular el nivel del líquido en el domo de un generador de vapor de gran capacidad, proceso este que reúne doble importancia. A saber:
Por ser inestable a lazo abierto, con respuesta inversa y aquí se le ha añadido el fatídico fenómeno del retardo también.
Ser un proceso, considerado como uno de los más importantes asociados al desempeño de los generadores de vapor, equipos industriales cuyo funcionamiento prácticamente determina la eficiencia de operación de toda central termoeléctrica, independientemente de su capacidad de generación. Para caso de estudio, se escogió la caldera piro-tubular BKG 25A, cuyo modelo para el nivel del agua en el domo es el siguiente (18):
(18)
Donde N representa el nivel de la mezcla hirviente en el domo y F a el flujo de agua a la caldera. Los tiempos se expresan en minuto, incluido el retardo que presenta el circuito de alimentación de agua el cual es de 0.4 min. Se precisa diseñar un PFC con un tiempo de establecimiento ante un cambio tipo paso en el set-point de 0.1 m aproximadamente.
El modelo anterior, sin el retardo, es totalmente equivalente al siguiente (19):
(19)
Se trata de un proceso de integración pura, inestable, en oposición a un proceso de primer orden normal, de ahí es que surge la RI precisamente. El modelo necesario para aplicar el PFC implica descomponer el integrador para desdoblarlo en dos procesos lineales superpuestos. El procedimiento es similar al aplicado en el caso 2. Se toma un periodo de muestreo T s = 0.1 min. El tiempo de respuesta deseado es TRLC = 20 min. El valor de H se toma bajo el criterio H = TRLC/2/T s = 20/2/0.1 = 100. La constante de tiempo de descomposición del integrado se toma T d = 3T = 3.6 min. Aplicando la metodología similarmente a como se hizo en los casos 1 y 2 se tiene finalmente para la señal de mando la siguiente (20):
(20)
Donde (21):
(21)
En este caso resulto: K 1 = 0.036 y K 2 = 0.018. Sustituyendo valores en (20) resulta:
El diagrama de simulación se muestra en la Fig. 8 y la respuesta, totalmente satisfactoria, se muestra en la Fig. 9:
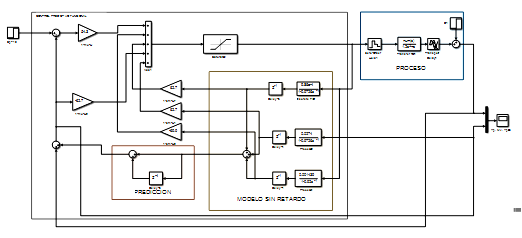(Elaboración propia)Figura 8 Simulación del PFC del nivel en el domo ante un cambio en la referencia de 10 mm y un disturbio del 5% en la carga.
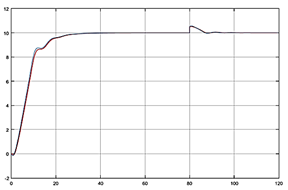(Elaboración propia)Figura 9 Respuesta en el nivel real de salida (rojo) y respuesta de la señal predicha (azul).
Caso de estudio 5: En este caso se utiliza el sistema control de temperatura basado en Arduino TCLab
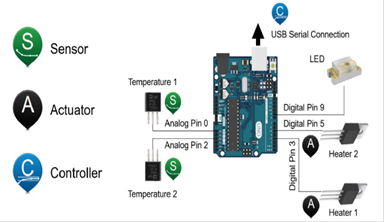
El sistema TCLab está formado por una placa montada sobre un Arduino modelo Leonardo [12, 13, 14, 15, 16, 17, 18, 19, 20, 21], consta de un LED, dos calentadores, que son los actuadores del sistema y dos sensores de temperatura. El calor generado por los calentadores se transmite a los sensores de temperatura. La motivación de sus autores [Universidad de Utah, USA] por la creación del TCLab es ayudar al diseño y a la práctica de la enseñanza real de cualquier algoritmo de control de procesos. Es un elemento práctico para ser usado en laboratorios de bajo coste y fácil uso, debido a su sencilla instalación, prácticamente plug-and-play y pequeño tamaño para reforzar los conocimientos de teoría de control adquiridos en la formación académica. Además, se disponen de bastantes recursos gratuitos en forma de video, tutoriales, aplicaciones, en diversos lenguajes, como Python o Matlab. En la Fig. 10 se muestra una vista exterior del minilabortario de control de temperatura.
A continuación se muestra un esquema de la estructura del TCLab. (Figura 11)
Se reportan varias aplicaciones del control de temperatura en el TCLab en base a los algoritmos PID, MPC, control óptimo LQR para cumplir este propósito [22], pero no se conoce de resultados utilizando la técnica PFC, siendo ese precisamente, el propósito principal en este caso, analizar el desempeño real de la temperatura del TCLab controlado por el PFC. Mediante identificación experimental se obtuvo el modelo de temperatura en el TCLab para la salida del sensor T 1 siguiente:
El retardo y la constante de tiempo están en segundo. El PFC se calcula siguiendo la metodología para un tiempo de respuesta en lazo cerrado de 50 s, con un periodo de muestreo de 1 s. La expresión para la señal de control es la siguiente (22):
(22)
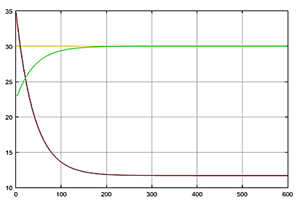
Se simula el sistema en simulink, considerando una condición inicial de la temperatura ambiente de 23 °C y aplicando la referencia R=30 °C constante. El comportamiento del sistema se muestra a continuación (Figura 12):
(Elaboración propia)Figura 12 Respuesta simulada del proceso del TCLab temperatura (verde), set-point (amarillo) y señal de mando (marrón).
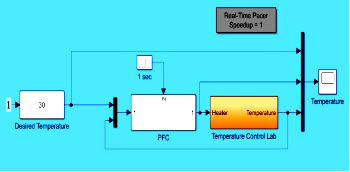
El PFC calculado se empotra en el sistema TCLab como se muestra a continuación (Figura 13):
(Elaboración propia)Figura 13 Esquema simplificado de la inclusión del PFC en TCLab con los mandos Simulink. El bloque PFC es el subsistema que incluye al controlador y al predictor.
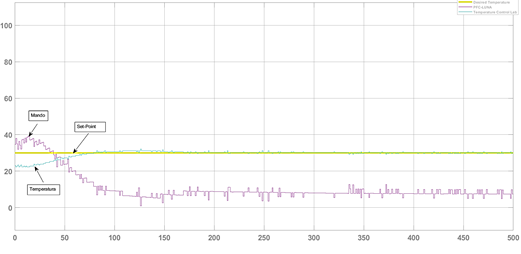
Los resultados del control de temperatura real por el PFC se muestran a continuación (Figura 14):
(Elaboración propia)Figura 14 Valores reales del set point (amarillo), temperatura (verde) y el mando (magenta).
Se puede apreciar la coincidencia totalmente satisfactoria entre la respuesta real de la temperatura en el TCLab controlado por el PFC y el valor obtenido mediante simulación.
Conclusiones
La investigación realizada infiere las siguientes conclusiones:
El PFC, en su modalidad más simple, basada en el cálculo de la señal de control a partir de una sola señal base, constituida por una señal tipo paso, constituye una herramienta valiosísima para la ingeniaría del control de procesos, convirtiéndose en una alternativa a los algoritmos clásicos y muy simple de aplicar mediante la tecnología digital.
Su simplicidad en el diseño quedó demostrada en procesos con dinámicas complejas como son los sistemas de alto orden, para lo cual se precisa el apoyo en los llamados modelos POR equivalentes, para los procesos inestables a lazo abierto debido a la presencia del efecto integral de la señal de entrada y en procesos con los indeseables fenómenos del retardo de transportación y la respuesta inversa.
Resulta interesante como el FPC compensa tales efectos del retardo y la RI de manera natural sin la necesidad de los conocidos compensadores de Smith y Linoya-Alpeter.
Igualmente curioso resulta la exactitud de estado estable lograda en todos los casos sin la necesidad de ninguna acción integral, con los consabidos efectos indeseables que ello puede causar en el clásico PID.
En el artículo queda evidenciado, mediante la aplicación al TCLab, que el PFC es aplicable de manera muy simple en un sistema digital basado en la tarjeta Arduino apoyado en MatLab-Simulink o cualquiera de los otros softwares disponibles para ello.
