Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Industrial
versión On-line ISSN 1815-5936
Ing. Ind. vol.33 no.2 La Habana mayo-ago. 2012
ARTÍCULO ORIGINAL
Optimización de los niveles de inventario en una cadena de suministro
Inventory levels optimization in a supply chain
José Antonio Díaz-Batista, Dania Pérez-Armayor
Instituto Superior Politécnico José Antonio Echeverría, Cujae. Facultad de Ingeniería Industrial. La Habana, Cuba.
RESUMEN
La gestión de inventarios es un tema muy estudiado por la Gestión de Operaciones y la Investigación de Operaciones para optimizar el costo de la gestión de los inventarios. Los modelos de inventario tradicionales generalmente trataban la optimización de inventarios para una organización individual. Pero recientemente ha comenzado a imponerse en la gestión empresarial el concepto de "cadena de suministro", donde la satisfacción de las necesidades del cliente final se logra mediante los flujos material, de información y financiero, que se establecen desde los proveedores originales hasta el último consumidor, requiriendo esto de un determinado nivel de cooperación e integración entre los participantes en la cadena. En este trabajo se estudia la optimización de los inventarios conjuntos suministrador-comprador, comparándolos con las políticas tradicionales no colaborativas, analizándose, como conclusión, las ventajas de este enfoque en los costos totales de inventario en la cadena.
Palabras clave: cadenas de suministro, inventarios, optimización.
ABSTRACT
Inventory management is a strongly observed subject in Operations Management and Operations Research, seeking for inventory management cost optimization. Traditional inventory models mainly deal with optimization inside a single enterprise. Yet, actually the supply chain concept has begun to overcome others approaches in the business management area. Supply chain management seeks customer satisfaction through material, financial and informational flows that are establish throughout the chain, from suppliers until the final consumer. This requires certain level of coordination and integration among supply chain members. This paper studies join supplier-buyer inventory optimization, comparing them with traditional non-collaborative policies, and analyzing advantages of this collaborative approach in the total inventory costs of the supply chain.
Key words: supply chains, inventories, optimization.
INTRODUCCIÓN
La gestión de los inventarios ha sido un tema muy estudiado por la Administración de Operaciones (Operations Management) [1] y la Investigación de Operaciones (Operations Research) [2], con el objetivo primordial de optimizar el costo de la gestión de los inventarios. Los modelos de inventario tradicionales generalmente trataban el caso de la optimización de los inventarios para una organización individual. Pero en los últimos tiempos ha comenzado a imponerse en la gestión empresarial el concepto de "cadena de suministro" [3], que consiste en un grupo de entidades independientes que han establecido relaciones de colaboración entre ellas, dada la necesidad de satisfacer la demanda de determinados productos o servicios que tienen sus clientes. La satisfacción de las necesidades del cliente final se logra mediante los flujos material, de información y financiero, que se establecen a través de la cadena desde los proveedores originales hasta el último consumidor, requiriendo esto de un determinado nivel de cooperación e integración entre los participantes en la cadena. En este trabajo se estudia la optimización de los inventarios conjuntos suministrador-comprador, como eslabón básico de la cadena, comparándolos con las políticas tradicionales no colaborativas, analizándose las ventajas de este enfoque en los costos totales de inventario en la cadena.
Dado el limitado número de modelos cuantitativos orientados a optimización de inventarios en cadenas de suministro e investigaciones en esta área, el análisis a continuación desarrolla un ejemplo utilizando contribuciones de Pan y Liao (1989) [4], Kelle y Miller (1998) [5] y Kelle, Al-Khateebb y Miller (2003) [6], para demostrar cuantitativamente las ventajas de la optimización de los inventarios conjuntos en el ambiente colaborativo de las cadenas de suministro.
MÉTODOS
Análisis general
Los costos de inventario constituyen uno de los más importantes costos logísticos de muchas empresas, representando una parte significativa de su costo total. Tradicionalmente, la modelación y optimización de los inventarios en una empresa contemplaba solo los costos internos de la misma, sin tomar en consideración la relación con sus suministradores.
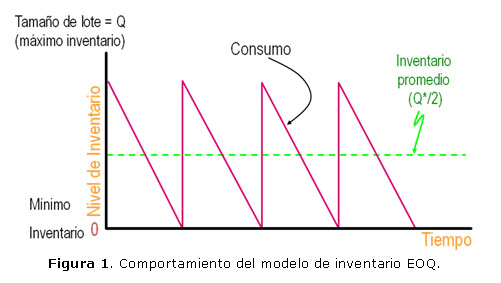
El modelo clásico de inventario EOQ (Economic Order Quantity) [1] es un ejemplo de ello y su comportamiento se muestra en la figura 1.
Considérese el caso de una Entidad I que sigue este modelo con los siguientes términos:
D = Demanda en unidades por año del producto
C = costo por unidad del producto (compra o producción)
S = Costo por pedido (o setup cost)
H = Costo de mantener en inventario una unidad por año
Entonces la cuantía del lote óptimo a pedir Q* es la conocida expresión 1:
Ésta corresponde a un costo mínimo total por año dado por la expresión 2:
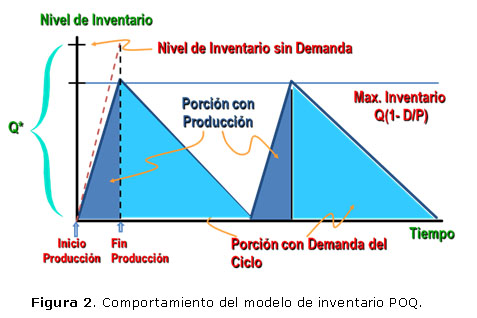
Supóngase también la existencia de otra Entidad II que cuenta con una capacidad de producción de P unidades por año para satisfacer la demanda anual D antes mencionada. En este caso, el comportamiento del inventario (modelo POQ -Period Order Quantity-) se muestra en la figura 2.
En esta situación, la cuantía del lote óptimo a producir Q* es la también conocida expresión 3:
Pero en una cadena de suministro el eslabón básico está constituido por la relación suministrador-comprador, y se pudiera hacer un símil y asumir que la Entidad I es el comprador y la Entidad II es el suministrador. Entonces se puede comprender fácilmente que los tamaños del lote económico para el suministrador (Qs*) y para el comprador (Qc*), en general, son diferentes, debido a la diferencia de sus costos y a que la política óptima individual para el suministrador no se corresponde con la política óptima individual para el comprador.
Luego, si la política que prevalece entre el suministrador y el comprador es "no colaborativa", cada uno de ellos trata de imponer el tamaño de lote que más le conviene, estableciéndose entonces una relación negativa de ganar-perder entre ambas entidades.
Pero si la política adoptada por ambas entidades es "colaborativa", como puede ser el caso en la mayoría de las entidades en Cuba, entonces es posible calcular un valor de lote óptimo conjunto que minimice el costo total para ambas entidades.
Análisis colaborativo
En el caso colaborativo, el costo total anual conjunto para el suministrador y el comprador se corresponde con la expresión 4:
Siendo la expresión 5, la utilizada para el lote óptimo conjunto QJ*.
Los resultados numéricos pueden comprobarse en el ejemplo a continuación.
Datos para el comprador:
D 1000 unidades por año
SC 225 $ por orden
CC 20 $ por unidad
HC 4 $ por unidad por año
Datos del suministrador:
P 2500 unidades por año
SS 100 $ por orden de producción
CS 10 $ por unidad producida
HS 1.8 $ por unidad por año
En la tabla 1 se muestran los resultados, calculados con las expresiones 1-5, de los costos anuales sin considerar los costos de producción (DCS) o de compra (DCC), que son constantes y no influyen en la optimización.
Como puede apreciarse en la tabla de resultados, la actividad colaborativa conjunta produce un menor costo total anual que las no colaborativas, lo que indica la conveniencia del trabajo colaborativo entre las entidades de la cadena de suministro.
Este resultado es de interés para las organizaciones cubanas, dado que la estructura y el nivel de subordinación de varias entidades al mismo ministerio u organización empresarial, pudiera y debiera facilitar el trabajo colaborativo.
Análisis colaborativo con enfoque justo a tiempo
Diversos estudios se han enfocado en los aspectos cualitativos del establecimiento de las relaciones suministrador-comprador que incluyen suministros justo-a-tiempo (JIT) en una cadena de suministro [7; 8; 9], pero han sido menos los que se han dedicado a modelos cuantitativos e investigaciones en esta área. Pan y Liao (1989), desarrollaron un modelo EOQ para un sistema de suministro JIT [4]. Posteriormente, Kelle y Miller (1998) aplicaron herramientas cuantitativas a la negociación suministrador-comprador en un entorno JIT [5].
En un entorno justo-a-tiempo el comprador requiere recibir envíos pequeños y frecuentes, lo que resulta en bajos costos de mantener el inventario para éste. Pero este requerimiento puede incrementar los costos del suministrador, entonces resulta conveniente una relación colaborativa.
Kelle, Al-Khateebb y Miller (2003), propusieron un interesante trabajo que aporta soporte cuantitativo al cálculo de los tamaños de lote óptimo para el suministrador y el comprador [6]. Dichos resultados son utilizados en esta sección.
En el análisis planteado por los autores anteriormente mencionados, se tiene que el lote QC requerido por el comprador debe ser entregado en n envíos de tamaño q (q = QC/n); entonces el suministrador puede producir un lote de tamaño QS que resulte un múltiplo de q, o sea, QS = mq. La solución del problema consiste en encontrar los valores óptimos de q, m y n.
Por lo que, asumiendo en este caso la misma notación utilizada anteriormente, en la que se han incluido los términos ZC y ZS que corresponden a costos fijos respectivos de recibir por el comprador y enviar por el suministrador los lotes de tamaño q, se tiene que el costo anual para cada uno de ellos es el indicado en las expresiones 6 y 7 [6]:
El costo total para el sistema queda reflejado en la expresión 8.
Para ello se emplea la notación de la expresión 9.
El tamaño del envío que minimiza el costo conjunto anual para el sistema puede ser expresado en función de m y n como se observa en la expresión 10.
Por último, el costo total en función de m y n es el mostrado en la expresión 11.
Luego, relajando los requerimientos de integridad para los valores de m y n, hallando las derivadas parciales de la función xJ(m,n)yJ(m,n) con respecto a m y n e igualándolas ambas a 0;- se pueden deducir las expresiones para los valores óptimos de m y n. Este proceso permite encontrar los valores óptimos n*, m* y qJ.
RESULTADOS
Con la utilización del mismo ejemplo numérico de la sección III y la adición de los valores ZC=1$ por envío y ZS=4.5 $ por envío; es posible calcular los valores óptimos de n*, m* y q*J, con el empleo de las expresiones 6-11 y las ofrecidas por Kelle, Al-Khateebb y Miller (2003) [6]. El proceso de cálculo es algo engorroso, pues para determinar n* y m*, se necesitan realizar varias iteraciones.
Como resultado de los cálculos se tienen los siguientes valores:
n* = 15 envíos por cada orden del comprador
m* = 10 envíos por cada lote producido por el suministrador
q*J = 65 unidades por cada envío del suministrador al comprador
QC = 975 unidades es el tamaño de la orden del comprador
QS = 650 unidades es el tamaño del lote producido por el suministrador
JCTJ = 938 $ por año, es el costo de la operación conjunta suministrador-comprador
A modo de comparación, se pueden realizar los cálculos para el caso en que m=n=1, es decir, QC=QS=qJ; que sería en el caso en que se realice un solo envío de magnitud igual al tamaño de la orden del comprador, siendo también igual el tamaño del lote a producir por el suministrador. Los resultados obtenidos son los siguientes:
n* = 1 envío por cada orden del comprador
m* = 1 envío por cada lote producido por el suministrador
q*J = 374 unidades por cada envío del suministrador al comprador
QC = 374 unidades es el tamaño de la orden del comprador
QS = 374 unidades es el tamaño del lote producido por el suministrador
JCTJ = 1766 $ por año, es el costo de la operación conjunta suministrador-comprador
Como puede apreciarse, el costo de esta última variante, que resulta operativamente más sencilla, es de 1766 $ por año, muy superior a la variante óptima anteriormente obtenida de 938 $ por año.
DISCUSIÓN
Como se explica anteriormente, la actividad colaborativa entre varias entidades produce un menor costo total anual que las actividades realizadas de forma individual. Sin embargo, el óptimo global pudiera (aparentemente) perjudicar los intereses individuales de alguno de los miembros de la cadena. Es entonces que se requiere un proceso de negociación entre las diferentes entidades (que por lo general no pertenecen a una misma organización) para acordar los valores de n y qJ más convenientes, en cuyo caso el análisis realizado en este trabajo permitiría evaluar las distintas alternativas y calcular posibles compensaciones entre las partes.
Teniendo en cuenta el análisis aquí realizado, sería pertinente recomendar la gestión del ámbito empresarial cubano en forma de cadenas de suministro, con el objeto de superar el marco estrecho de las decisiones óptimas individuales y trabajar hacia la obtención de los beneficios del enfoque colaborativo antes descrito. La gestión de cadenas de suministro entre empresas de diferentes organizaciones podría ser fácilmente adoptada por el sistema empresarial nacional, dado que la estructura y el nivel de subordinación vigente en el país pudiera y debiera facilitar el trabajo colaborativo.
CONCLUSIONES
A partir del análisis anteriormente expuesto, se ha arribado a las siguientes conclusiones:
1. El análisis cuantitativo de los problemas de inventario ha probado ser una herramienta importante para la toma de decisiones acerca de las variables principales que definen el comportamiento y costo de los inventarios.
2. En este sentido, el análisis colaborativo de los problemas de inventario en las cadenas de suministro ha venido a sustituir el análisis individual tradicional que realizaban las organizaciones, sustituyendo las políticas de ganar-perder por las de ganar-ganar.
3. El análisis colaborativo aquí descrito y su enfoque justo-a-tiempo, constituyen herramientas que pueden utilizar las organizaciones cubanas que gestionan cadenas de suministro en que están involucradas varias entidades de las propias organizaciones, siendo posible superar en estos casos, el marco estrecho de las decisiones óptimas individuales que no se corresponden con el óptimo de la cadena de suministro en su conjunto.
4. Por otra parte, si las entidades del eslabón suministrador-comprador que componen la cadena, no perteneciesen a la misma organización, entonces sería necesaria una negociación para acordar los valores de n y qJ más convenientes para ambas entidades, en cuyo caso el análisis realizado en este trabajo permitiría evaluar las distintas alternativas y calcular posibles compensaciones entre las partes.
5. En consecuencia, se consideran pertinentes las siguientes recomendaciones:
- Fomentar la gestión de cadenas de suministro en el ámbito empresarial cubano, dada la necesidad de superar el marco estrecho de las decisiones óptimas individuales.
- Fomentar la utilización en organizaciones cubanas del análisis colaborativo aquí descrito, recomendando con un enfoque justo-a-tiempo.
- Tener en cuenta en las negociaciones entre entidades suministradoras o compradoras que no pertenecen a la misma organización, los valores de n y qJ, así como calcular las posibles compensaciones más convenientes para ambas entidades, sirviéndose para ello del análisis realizado en este trabajo.
REFERENCIAS
1. SCHROEDER, R. G., Administración de Operaciones, Boca Ratón (EE.UU), McGraw-Hill, 2005, ISBN 9701046536, cap. 15.
2. HILLIER, F. S.; LIEBERMAN, G. J., Investigación de Operaciones, Boca Ratón (EE.UU), McGraw Hill, 2002, ISBN 9701034864.
3. BALLOU, R. H., Logística, Administración de la cadena de suministro, México, D. F., Prentice-Hall, 2004, ISBN 970-26-0540-7.
4. PAN, A. C.; LIAO, C., «An inventory model under just-in-time purchasing agreements», Production and Inventory Management [en línea], 1989, vol. 30, no. 1, pp. 49-52 [consulta: 2011-03-04], ISSN 0144-3577. Disponible en: <doi: 10.1108/01443579810192907>
5. KELLE, P.; MILLER, P. A., «Quantitative support for buyer_supplier negotiation in JIT purchasing» International Journal of Purchasing and Materials Management, 1998, vol. 34, no. 2, pp. 25-30, ISSN 1055-6001.
6. KELLE, P.; AL-KHATEEBB, F.; MILLER, P. A., «Partnership and negotiation support by joint optimal ordering/setup policies for JIT» International Journal of Production Economics, 2003, vol. 81-82, Proceedings of the Eleventh International Symposium on Inventories, pp. 431_441, ISSN 0925-5273.
7. AKACUM, A.; DALE, B. G., «Supplier partnering: Case study experiences» International Journal of Purchasing and Materials Management, 1995, vol. 31, no. 1, pp. 38-44, ISSN 1474-6085.
8. NEWMAN, R. G., «The buyer_supplier relationship under just-in-time» Production and Inventory Management, 1988, vol. 29, no. 3, pp. 45-49, ISSN 1474-6085.
9. RICHESON, L.; LACKEY, C. W.; STARNER, J. W., «The effect of communication on the linkage between manufacturers and suppliers in a just-in-time environment», International Journal of Purchasing and Materials Management [en línea], 1995, vol. 31, no. 1, pp. 21_28 [consulta: 2011-02-23], ISSN 1055-6001. Disponible en: <doi: 10.1111/j.1745-493X.1995.tb00276.x>
Recibido: 7 de abril de 2011
Aprobado: 9 de enero de 2012
José Antonio Díaz-Batista. Instituto Superior Politécnico José Antonio Echeverría, Cujae. Facultad de Ingeniería Industrial. La Habana, Cuba. Correo electrónico: diaztony@tesla.cujae.edu.cu













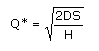 (1)
(1) 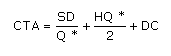 (2)
(2) 
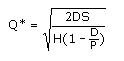 (3)
(3) 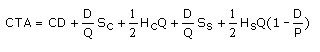 (4)
(4) 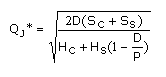 (5)
(5)  (6)
(6) 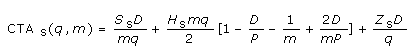 (7)
(7) 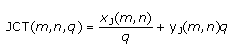 (8)
(8) 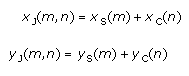 (9)
(9) 