I. INTRODUCCIÓN
La regresión múltiple, el análisis factorial, el análisis multivariante de la varianza y el análisis discriminante son las técnicas más comunes dentro del conjunto de técnicas multivariadas. Constituyendo cada una de estas una poderosa herramienta a la hora de tratar un amplio abanico de cuestiones prácticas y teóricas, pero poseen una limitación común: solo pueden evaluar una restricción al mismo tiempo [1].
Los Modelos de Ecuaciones Estructurales (MEE) permiten examinar simultáneamente una serie de relaciones de dependencia. De acuerdo con Kahn (2006) y Palacios Copete y Suarez Kimura (2017) los modelos de ecuaciones estructurales son una extensión de varias técnicas multivariadas como la regresión múltiple y el análisis factorial. Sin embargo, posee algunas características particulares que lo diferencian de las otras técnicas multivariadas, destacándose dentro de estas la capacidad de estimar y evaluar la relación entre variables latentes o no observables. Dichos modelos constituyen una herramienta útil para el estudio de relaciones causales de tipo lineal, no prueban la causalidad, pero ayudan a los investigadores en la toma de decisiones, rechazando las hipótesis causales cuando se contradicen con los datos [2; 3].
Los MEE han sido utilizados en importantes y disimiles estudios. El ámbito de las Tecnologías de la Información (TI) también ha sido escenario de estudio mediante modelos de ecuaciones estructurales. Varias investigaciones como las de Ortega et al. (2007),Ham et al. (2008),Zhang et al. (2007),Fernández et al. (2010), reflejan su empleo en el estudio de los sistemas de información y su aceptación en empresas de diferentes sectores [4; 5; 6; 7].
Por su parte,Leidner et al. (2010), estudia la influencia de la innovación en TI sobre los centros hospitalarios. Desarrolla un modelo que sugiere que aquellos hospitales que son innovadores de las TI pueden sacar un mayor provecho de estas tecnologías, lo que a su vez resultará en un mejor rendimiento del hospital. Otro aspecto que se comprueba es que la dirección estratégica de los funcionarios de información principal y la actitud hacia las TI de los equipos de gestión dentro de los hospitales son factores claves que influencian la innovación en este ámbito [8].
Según Bulchand Gidumal y Melián González (2011) las TI tienen una influencia positiva en la mejora del rendimiento de las organizaciones; demuestra empíricamente que la planeación y gestión de TI influencian los recursos de la organización, tanto físicos como humanos [9]. Esto consecuentemente trae efectos positivos en cada una de las áreas relacionadas con TI que usualmente se encuentran en una organización, y a su vez el funcionamiento de estas áreas influencia en el impacto positivo que tienen las TI en el rendimiento organizacional.
En investigaciones precedentes se encuentra que las definiciones de gestión de TI que se abordan en la literatura, reflejan que no existe consenso con relación al alcance del contenido de este concepto. Las investigaciones teóricas realizadas por Pérez Lorences (2014) asume que la gestión de TI incluye el proceso de toma de decisiones relativas a las TI, vinculado a los objetivos presentes y futuros del negocio y abarca la planificación, construcción, ejecución y control de TI. En este sentido, las aristas fundamentales de este concepto son la organización de TI, la alineación y la gestión de riesgos, incorporando la implementación de buenas prácticas como criterio de medida para evaluar el nivel de gestión de TI en una empresa [10].
En varios estudios realizados se demuestra la importancia que para el negocio de las organizaciones tiene de manera individual cada uno de los componentes que conforman la Gestión de las Tecnologías de la Información (GTI). Sin embargo, no ha sido probada empíricamente la interrelación que existe entre todas las aristas de la gestión de TI, empleando métodos estadísticos o matemáticos que den fundamento y credibilidad a dicha relación.
En consecuencia, la presente investigación tiene como objetivo principal comprobar la relación existente entre los componentes de la GTI utilizando los MEE. Para ello se pretende construir un modelo teórico de las interrelaciones entre los componentes de la gestión de TI. Se parte de la revisión detallada de la bibliografía, comprobar el cumplimiento de las condiciones necesarias para aplicar un análisis factorial confirmatorio. Se valida el modelo propuesto empleando varias pruebas de bondad de ajuste e interpretar los resultados obtenidos a partir de la estimación de los parámetros del modelo validado.
II. MÉTODOS
La información necesaria para la realización de la presente investigación se obtuvo a partir del cuestionario de gestión de TI, aplicado por Díaz Ibarra (2012) en un estudio precedente en la provincia de Villa Clara [11]. En este estudio la población se definió como: las empresas estatales, sociedades anónimas con dependencias en el territorio, grupos empresariales y empresas nacionales con UEB en la provincia que tenían tecnologías de la información que apoyaran en alguna medida sus objetivos empresariales. La muestra seleccionada incluye a 93 empresas del territorio.
Los datos recolectados se analizan con los MEE, específicamente el Análisis Factorial Confirmatorio (AFC). Dicho análisis es una técnica para confirmar las relaciones entre las variables observadas y las variables latentes del modelo de medida propuesto, así como confirmar el ajuste entre dicho modelo y los datos empíricos recuperados.
Para llevar a cabo este análisis varios son los autores que proponen una serie de fases a tener en cuenta en dicho proceso. Al respecto García Veiga (2011), Guàrdia Olmos (2016),Medrano y Muñoz-Navarro (2017) coinciden que en el desarrollo de un modelo de ecuaciones estructurales es necesario desarrollar cuatro fases: la especificación, la identificación, la estimación y, por último, la evaluación y la interpretación de dicho modelo [12; 13; 14]. Cada una de estas fases se tienen en cuenta en el desarrollo de la presente investigación.
III. RESULTADOS
Fase de especificación
En esta fase se realizó el planteamiento de las ecuaciones matemáticas; donde habrá tantas ecuaciones estructurales como constructos latentes, explicadas por otras variables (latentes u observadas).Se formularon los enunciados sobre el conjunto de parámetros, decidiendo entre los que serán libres para ser estimados o fijos, a los que se les asignará un valor dado, normalmente cero. Se especificaron los supuestos estadísticos sobre las fuentes de variación y en concreto sobre la forma de distribución conjunta, que en la mayoría de las técnicas empleadas se considera normalidad multivariante. Por último, se precisó el comportamiento de las variables no incluidas en el modelo, cuyo efecto se recoge en los términos del error de medida o de perturbación.
Cada una de las variables latentes y observables empleadas en la construcción del modelo teórico en la presente investigación se encuentran definidas en la investigación realizada por Pérez Lorences (2014); las variables latentes se hicieron corresponder con cada uno de los componentes que conforman la gestión de TI y se consideraron como variables observables aquellas que se creyeron más idóneas en la medición de las variables latentes [10].
En la tabla 1 se presentan las variables utilizadas en el cuestionario, las que se corresponden totalmente con el modelo que se desea comprobar y presentan un nivel de medición ordinal, midiéndose en un intervalo de 1 a 5.
Tabla 1 Variables latentes e indicadores utilizados en el cuestionario
| Variables latentes | Variables observables (indicadores) |
|---|---|
| Xi1: Nivel de organización de TI | X1: Nivel de definición de estructuras. |
| X2: Nivel de definición de procesos. | |
| X3: Nivel de definición de mecanismos relacionales. | |
| Xi2: Grado de alineación TI/Negocio | X4: Grado de alineación estratégica. |
| X5: Grado de alineación estructural. | |
| X6: Grado de alineación social. | |
| Xi3: Nivel de gestión de riesgos de TI | X7: Nivel de importancia percibida. |
| X8: Nivel de participación de la alta dirección. | |
| X9: Nivel de implementación de prácticas de gestión de riesgos. | |
| X10: Nivel de percepción de la responsabilidad. | |
| Xi4: Nivel de implementación de buenas prácticas de gestión de TI | X11: Nivel de implementación de estándares internacionales. |
| X12: Nivel de implementación de la evaluación de proyectos de inversión. | |
| X13: Nivel de implementación de monitoreo del desempeño. |
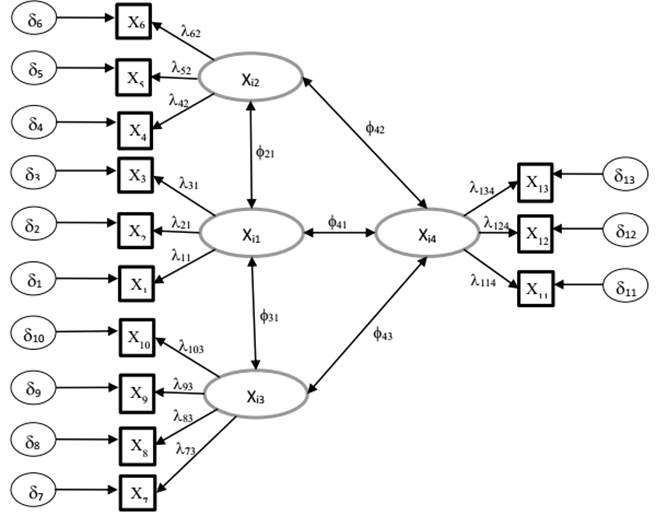
A partir de estas variables se elaboró tal y como se muestra en la figura 1 el planteamiento del modelo teórico. En este se pueden apreciar las relaciones entre las variables latentes, así como los respectivos indicadores utilizados para medir cada una de estas.
Teniendo en cuenta cada una de las correlaciones planteadas entre los diferentes componentes de la GTI se definieron para el modelo las hipótesis siguientes:
H1: El grado de alineación entre TI y el negocio y el nivel de organización de TI en una empresa están significativamente correlacionados.
H2: El nivel de gestión de riesgos de TI y el nivel de organización de TI en una empresa están significativamente correlacionados.
H3: El grado de alineación entre TI y el negocio y el nivel de implementación de buenas prácticas de gestión de TI están significativamente correlacionados.
H4: El nivel de organización de TI en una empresa y el nivel de implementación de buenas prácticas de gestión de TI están significativamente correlacionados.
H5: El nivel de gestión de riesgos de TI y el nivel de implementación de buenas prácticas de gestión de TI están significativamente correlacionados.
El modelo permitió comprobar a partir de la aplicación del AFC si las variables observables planteadas en el cuestionario miden realmente cada variable latente especificada.
El AFC es un procedimiento de análisis encuadrado en los modelos de ecuaciones estructurales, cuyo propósito se centra en el estudio de los modelos de medida. Se analizan las relaciones entre un conjunto de indicadores o variables observadas y una o más variables latentes o factores. Es utilizado para observar si un conjunto de variables observadas explica un factor latente; observando si las variables que componen un constructo varían todas juntas, y si el constructo es afectado cuando tales variables entran o salen del modelo, o si crecen o decrecen. El objetivo más importante es determinar cuánto la covarianza propuesta ajusta la covarianza observada, en otras palabras, si las relaciones entre las variables en el modelo hipotético se parecen a las relaciones entre las variables en el conjunto de datos observados [15].
Análisis de condiciones necesarias para aplicar el AFC
El modelo incluyó un total de 13 indicadores y 4 variables latentes por lo que se cumple el límite para un modelo ideal (no más de 30 indicadores y 6 variables latentes). Se cumplió que la cantidad de indicadores por variable latente es superior a 2, pues se cuenta con al menos 3 indicadores por cada variable latente. En todos los casos se confirmaron las condiciones del nivel de medida y cantidad de valores por indicador, al contarse con variables ordinales con 5 niveles (el mínimo es 4).
La presencia de normalidad multivariada es otro de los requisitos que cualquier conjunto de datos debe reunir para la aplicación de la mayoría de los métodos de estimación de los MEE. En primer lugar, debe satisfacerse la normalidad univariada de todas las variables, para ello se analizaron los valores de asimetría y curtosis; obteniéndose los resultados que a continuación se muestran en la tabla 2.
Tabla 2 Resultados de las pruebas de asimetría y curtosis
| Variable observable | N | Asimetría | Curtosis | ||
|---|---|---|---|---|---|
| Coeficiente | Error típico | Coeficiente | Error típico | ||
| X1 | 93 | -0,276 | 0,250 | -1,265 | 0,495 |
| X2 | 93 | 0,45 | 0,250 | -0,929 | 0,495 |
| X3 | 93 | -0,124 | 0,250 | -0,374 | 0,495 |
| X4 | 93 | -0,0115 | 0,250 | 0,224 | 0,495 |
| X5 | 93 | -0,689 | 0,250 | 0,627 | 0,495 |
| X6 | 93 | -0,124 | 0,250 | -0,374 | 0,495 |
| X7 | 93 | -1,425 | 0,250 | 1,843 | 0,495 |
| X8 | 93 | -1,331 | 0,250 | 2,138 | 0,495 |
| X9 | 93 | -1,243 | 0,250 | 1,950 | 0,495 |
| X10 | 93 | -0,962 | 0,250 | 0,637 | 0,495 |
| X11 | 93 | 0,130 | 0,250 | -0,881 | 0,495 |
| X12 | 93 | -0,296 | 0,250 | -1,652 | 0,495 |
| X13 | 93 | -0,255 | 0,250 | -1,701 | 0,495 |
Con los resultados anteriores y teniendo en cuenta que, valores por encima de |3,00| indicarían asimetría extrema, mientras que para el caso de la curtosis, valores entre |8,00| y |20,00| corroborarían situaciones de curtosis extrema y valores por encima de |20,00| indicarían un serio problema de normalidad [12]. Se concluyó que hay inexistencia de problemas de asimetría y curtosis en las variables observadas, por lo que se cumple el requisito de normalidad univariada.
En aras de comprobar el requisito de normalidad multivariada se procedióal cálculo del coeficiente de Mardia; tal y como se muestra en la expresión 1.
Cuando dicho coeficiente es inferior al valor de la expresión 1, se puede concluir que se está en presencia de normalidad multivariada de los datos. El coeficiente de Mardia, también se conoce como de curtosis multivariada. Para el modelo en cuestión se obtuvo un valor de dicho coeficiente de 1,301, por lo que se comprueba la condición de normalidad multivariada de los datos. De esta forma es posible la utilización del método de estimación de máxima verosimilitud en el análisis.
Con el estudio de la distribución univariada y multivariada de los datos, se demostró que en el modelo no hay multicolinealidad. La multicolinealidad tiene lugar cuando variables diferentes miden de hecho el mismo constructo, lo que implica una correlación muy elevada entre ellas (del orden de 0,90 o superior).
Para detectar la multicolinealidad se examinó la matriz de correlaciones que se muestra en la tabla 3, en función de detectar variables con rxy>0,90. Como se pudo observar, cada uno de los coeficientes es menor que 0,90 lo que indica la ausencia de multicolinealidad en los datos.
Tabla 3 Matriz de correlaciones, medias y desviaciones típicas de las variables observables
|
|
|
|
|
|
|
|
|
|
|
|
1 | |||||||
|
|
0,222 | 1 | ||||||
|
|
0,222 | 0,351 | 1 | |||||
|
|
0,25 | 0,502 | 0,205 | 1 | ||||
|
|
0,206 | 0,425 | 0,082 | 0,391 | 1 | |||
|
|
0,113 | 0,02 | 0,108 | 0,052 | -0,034 | 1 | ||
|
|
0,122 | 0,439 | 0,403 | 0,512 | 0,267 | 0,193 | 1 | |
|
|
0,188 | 0,398 | 0,342 | 0,494 | 0,285 | 0,086 | 0,611 | 1 |
|
|
0,316 | 0,355 | 0,322 | 0,377 | 0,234 | 0,115 | 0,568 | 0,675 |
|
|
0,061 | 0,351 | 0,177 | 0,379 | 0,225 | 0,076 | 0,486 | 0,582 |
|
|
0,117 | 0,171 | 0,184 | 0,18 | 0,243 | 0,018 | 0,151 | 0,177 |
|
|
0,249 | 0,22 | 0,145 | 0,354 | 0,181 | -0,049 | 0,25 | 0,335 |
|
|
0,221 | 0,37 | 0,218 | 0,361 | 0,083 | 0,043 | 0,267 | 0,34 |
| 3,52 | 3,59 | 3,53 | 3,59 | 3,41 | 3,06 | 4,38 | 4,08 | |
| 1,427 | 0,947 | 0,916 | 0,811 | 1,013 | 1,405 | 0,871 | 0,947 | |
|
|
|
|
|
|
|
|||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
1 | |||||||
|
|
0,517 | 1 | ||||||
|
|
0,095 | 0,22 | 1 | |||||
|
|
0,239 | 0,232 | 0,186 | 1 | ||||
| 0,384 | 0,241 | 0,154 | 0,367 | 1 | ||||
| 4,38 | 4,11 | 1,9 | 3,08 | 3,08 | ||||
| 0,721 | 0,853 | 0,693 | 1,663 | 1,702 |
Fue útil y necesario analizar la fiabilidad de los datos, para cuyo estudio se empleó el estadístico Alpha de Cronbach. Una de las ventajas que trae consigo la utilización de este estadístico reside en que ofrece la posibilidad de evaluar cuánto mejoraría o empeoraría la fiabilidad del índice si se excluyera un determinado ítem.
Para el total de ítems se obtuvo un Alpha de Cronbach de 0,78 lo cual se considera aceptable (mayor que 0,7). Considerando los resultados de la tabla 4, que reflejan la variación de los cálculos si es eliminado alguno de los ítems del cuestionario, no resultó factible dejar fuera del análisis a ninguno de estos. Solo en el caso de uno de los ítems (X6) se produce un aumento, pero este no resulta significativo.
Tabla 4 Variación del estadístico Alpha deCronbach
| Var | X 1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,77 | 0,75 | 0,76 | 0,75 | 0,77 | 0,80 | 0,75 | 0,74 | 0,75 | 0,76 | 0,77 | 0,77 | 0,76 |
Además, se realizó el análisis de la fiabilidad para cada variable latente del modelo obteniéndose los resultados de la tabla 5. Como se observa las variables Xi1, Xi2 y Xi4 presentan un nivel de fiabilidad bajo. Estos valores no impiden el uso de los datos y pueden estar relacionados con el hecho de cada uno de los constructos sea medido por un pequeño número de ítems.
Luego de los análisis realizados se pudo comprobar que se cumplen satisfactoriamente cada una de las condiciones necesarias para aplicar el AFC.
Fase de identificación
Un modelo estará identificado si los parámetros del modelo completo (modelo estructural y modelo de medida, juntos) pueden estimarse a partir de los elementos de la matriz de covarianzas de las variables observables. La regla conocida como regla del conteo, se emplea para identificar los modelos de ecuaciones estructurales. El número total de variables se denota como se muestra en la expresión 2.
Por consiguiente, el número de elementos no redundantes se calcula según la expresión 3.
Se denota al número total de parámetros a ser estimados en el modelo como t, por lo que para realizar la identificación del modelo se debe cumplir como condición necesaria que t sea menor o igual que el valor de la expresión 3. Si se tiene la igualdad, se dice que el modelo está identificado. Si t es estrictamente menor que ½ s(s+1), se dice que el modelo está sobre identificado y si t es mayor que ½ s(s+1), entonces el modelo no está identificado.
Planteamiento del modelo de ecuaciones estructurales. Identificación
A partir del análisis anterior se procedió a detallar el modelo de ecuaciones estructurales inicial, así como los diferentes parámetros a estimar, información que se muestra a continuación en la figura 2.
Variables latentes
Variables observables
Errores de medida
Coeficientes de regresión
Relacionan las variables latentes con las observadas (cargas factoriales): λij
Representan la covariación entre las variables latentes exógenas: Φ21, Φ31, Φ41, Φ42, Φ43
En el modelo de ecuaciones estructurales planteado se tiene que el número total de variables observables exógenas es q=13, variables endógenas p=0, por lo que da un total de variables de s=13. Teniendo en cuenta esto el número de elementos no redundantes calculado según la expresión 3 es 91 y el número total de parámetros del modelo a ser estimados es t=31. Por tanto, dado que el valor de t es estrictamente menor que el número de elementos no redundantes, se puede afirmar que el modelo se encuentra sobre identificado, por lo que el modelo cumple la condición necesaria para estar identificado.
Fase de estimación
Según Cupani (2012), la estimación consiste en determinar los valores de los parámetros desconocidos y su respectivo error de medición. Como en la regresión múltiple, se estiman los coeficientes no estandarizados y estandarizados de los parámetros [1]. Máxima verosimilitud es una de las técnicas ampliamente empleadas en la mayoría de los programas informáticos para la estimación de los MEE, por ser eficiente y no sesgada siempre que se cumplan los supuestos de normalidad multivariada, resulta más apropiada su aplicación cuando el tamaño de muestra es pequeño.
Estimación y evaluación del modelo
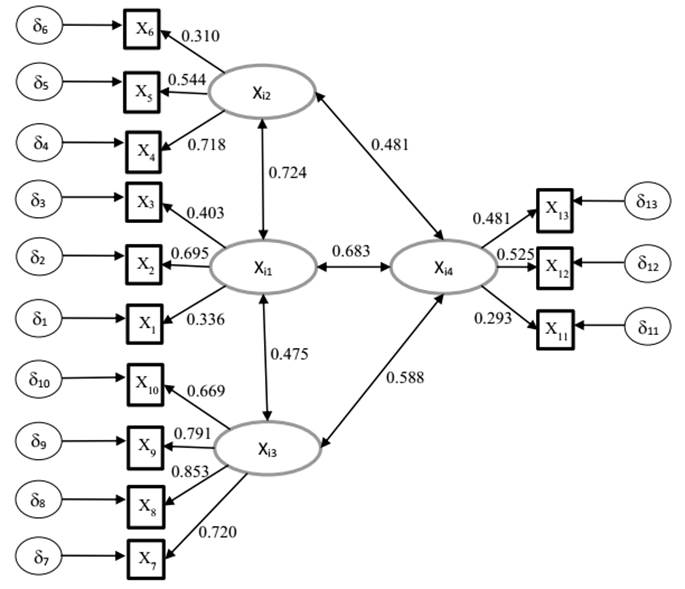
Una vez elaborado el modelo inicial y desarrollado tanto el análisis descriptivo de los datos como la identificación del modelo se procedió a la estimación de los parámetros del modelo. Se emplea el método de máxima verosimilitud en virtud de la existencia de normalidad multivariada de los datos.
Las cargas factoriales del modelo que se muestran en la figura 3 oscilan entre 0,310 y 0,853 apareciendo el constructo que representa el nivel de gestión de riesgos de TI como uno de los constructos mejor definidos. Se tiene la correlación más alta entre los constructos Xi1 y Xi2 (nivel de organización de TI y grado de alineación TI/Negocio respectivamente). Con un valor de 0,724; mientras que la correlación más baja se establece entre el nivel de organización de TI y el nivel de gestión de riesgos de TI (Xi1 y Xi3 respectivamente) con un valor de 0,475.
Una vez estimados los parámetros del modelo, se procedió a examinar la significación estadística de cada carga obtenida entre el indicador y la variable latente correspondiente. En la tabla 6 se muestran las estimaciones de los parámetros del modelo, el error estándar aproximado (S.E.), la proporción crítica (C.R.) y las estimaciones estandarizadas de los parámetros.
Tabla 6 Estimaciones por máxima verosimilitud
| Estimate | S.E. | C.R. | P | S.Estimate | ||
|---|---|---|---|---|---|---|
| NIP.4.1 (X7) | <--- Xi3 | 1,000 | 0,720 | |||
| NPAD.4.2 (X8) | <--- Xi3 | 1,288 | 0,177 | 7,256 | 0,000 | 0,853 |
| NIPGR.4.3 (X9) | <--- Xi3 | 0,910 | 0,132 | 6,909 | 0,000 | 0,791 |
| NDE.2.1 (X1) | <--- Xi1 | 1,000 | 0,336 | |||
| NDP.2.2 (X2) | <--- Xi1 | 1,311 | 0,513 | 2,553 | 0,011 | 0,695 |
| NDMR.2.3 (X3) | <--- Xi1 | 0,764 | 0,347 | 2,202 | 0,028 | 0,403 |
| GAECA.3.1 (X4) | <--- Xi2 | 1,000 | 0,718 | |||
| GAEAL.3.2 (X5) | <--- Xi2 | 0,947 | 0,296 | 3,204 | 0,001 | 0,544 |
| GAS.3.3 (X6) | <--- Xi2 | 0,689 | 0,307 | 2,245 | 0,806 | 0,310 |
| NPR.4.4 (X10) | <--- Xi3 | 0,910 | 0,154 | 5,913 | 0,000 | 0,669 |
| NIEI.5.1 (X11) | <--- Xi4 | 1,000 | 0,293 | |||
| NIEPI.5.2 (X12) | <--- Xi4 | 4,225 | 2,114 | 1,999 | 0,046 | 0,525 |
| NIMD.5.3 (X13) | <--- Xi4 | 4,891 | 2,405 | 2,034 | 0,042 | 0,598 |
La proporción crítica es el resultado de dividir la estimación del parámetro y la estimación del error estándar. Si a una estimación le corresponde una proporción crítica mayor que 1,96, el parámetro es significativamente diferente de cero al nivel 0,05. Teniendo en cuenta esto y los resultados de la tabla anterior se llegó a la conclusión de que todos los valores de proporción crítica son mayores que 1,96, por lo que, en consecuencia, todos los parámetros estimados son significativos. Una vez examinada la significación de las cargas, se procedió a evaluar la fiabilidad de cada uno de los indicadores (proporción de varianza que tiene en común con el constructo), mostrándose el resultado de este análisis la tabla 7.
Tabla 7 Fiabilidad de la medida o varianza explicada en la variable por el constructo
| Variable | X1 | X2 | X3 | X4 | X5 | X6 | X7 |
| Estimación | 0,336 | 0,695 | 0,403 | 0,718 | 0,504 | 0,031 | 0,720 |
| Variable | X8 | X9 | X10 | X11 | X12 | X13 | |
| Estimación | 0,853 | 0,791 | 0,669 | 0,293 | 0,525 | 0,598 |
Una vez analizados los resultados anteriores se llegó a la conclusión de que cada una de las variables observables no tiene el mismo nivel de impacto sobre las variables latentes. Se demostró que las variables observables que mejor miden cada uno de los constructos son: X2 en el caso de organización, X4 para la alineación de TI/negocio, X8 en la gestión de riesgos y X13 para la variable latente de implementación de buenas prácticas.
Para evaluar la calidad del modelo una vez estimados los parámetros se analizó su ajuste. Varias investigaciones como las de Agarwal et al. (2019), Ainin et al. (2016), Sharma (2018), Sica et al. (2019) muestran como en la actualidad, la combinación más extendida y utilizada de estos estadísticos es la siguiente: Chi-cuadrado (χ2), el Error de Aproximación Cuadrático Medio (RMSEA, por sus siglas en inglés), la Raíz del Residuo Cuadrático Promedio(SRMR, por sus siglas en inglés),el Índice de Bondad de Ajuste (GFI, por sus siglas en inglés) y el Índice de Bondad de Ajuste Comparativo (CFI, por sus siglas en inglés). El análisis e interpretación de este conjunto de índices resulta suficiente como para poder tomar una decisión en cuanto al ajuste del modelo en cuestión [16; 17; 18; 19].
Estadísticos de bondad de ajuste absoluto
La evaluación global del modelo permitió determinar en qué medida el modelo inicial reproduce adecuadamente las relaciones que existen en la matriz de covarianzas de los datos empíricos. Evaluando los resultados que se muestran en la tabla 8 y teniendo en cuenta los criterios utilizados por Mirzaie et al. (2019), Sunthonwutinun y Chooprayoon (2017)en relación a cada estadístico de ajuste [20; 21], se obtuvo que momentáneamente (debido a que solo se ha tenido en cuenta el análisis global) no existen diferencias significativas entre el modelo estimado y los datos si se tiene en cuenta que:
Se obtuvo un valor del estadístico χ2de 88,794 con 60 grados de libertad (GL) y una probabilidad (P) asociada de 0,009. (χ2: 0 ≤ 88,794 ≤ 120. Es necesario destacar que aun cuando la probabilidad asociada no es la recomendada, la razón Chi-Cuadrado/GL (χ2/GL) es más fiable para garantizar la adecuación del modelo estimado a los datos [12].
Razónχ2/GL: 1,480 < 3 y 0 ≤ 1,480 ≤ 2.
El valor de GFI es de 0.900 (valor inferior para el rango de un buen ajuste).
La SRMR es de 0,090 (< 0,10).
Fase de evaluación e interpretación
Una vez se determinó que el modelo está identificado y se ha realizado la estimación de los parámetros. Solo restan dos pasos que resultan fundamentales para cualquier análisis: la evaluación e interpretación del mismo a fin de contrastar si los datos se han ajustado al modelo propuesto. La utilidad del modelo vendrá dada por su capacidad para explicar la realidad observada. Esta capacidad debe evaluarse tanto para el conjunto del modelo, como para cada una de las relaciones expresadas en él.
Para evaluar la calidad del modelo se utilizaron varios estadísticos de bondad de ajuste. Según Schreiber et al. (2006), ninguno de estos aporta toda la información necesaria para valorar el modelo [22]; habitualmente se utiliza un conjunto de ellos del que se informa simultáneamente [23; 24; 25].
IV. DISCUSIÓN
A partir del análisis de los resultados se puede concluir que el modelo propuesto, a partir de la teoría existente para identificar las interrelaciones entre los diferentes componentes de la GTI, ha quedado validado empíricamente empleando los MEE. Según Castellanos Ramírez (2015), este análisis permite sentar las bases para el diseño de indicadores complejos para medir la GTI. Constituye el punto de partida para realizar estudios de mayor complejidad que permitan demostrar la influencia de estos componentes en otros indicadores organizacionales [26]. Esto último permitirá a la empresa enfocarse en uno o más componentes de la GTI para establecer acciones de mejoramiento.
Uno de los aportes más destacados del modelo es que permite evidenciar estadísticamente la interrelación existente entre cada uno de los componentes de la GTI. Los resultados obtenidos, teniendo en cuenta los coeficientes de regresión que representan la covariación entre las variables latentes, permiten comprobar todas las hipótesis planteadas. Sin embargo, los resultados también muestran diferentes niveles de interrelación entre los distintos componentes.
En este sentido destacan positivamente la interrelación existente entre el nivel de organización de TI dentro de la empresa y el grado de alineación TI/negocio, siendo estos los elementos que revelaron mayor grado de correlación, seguido por la interrelación entre el nivel de organización de TI y el nivel de implementación de buenas prácticas de gestión de TI. Ambos resultados muestran que el componente de la gestión de TI que tiene mayor correlación con otros componentes es la organización de TI. Sin embargo, los resultados revelan que este componente fue el de más baja correlación con el nivel de gestión de riesgos. Siendo también menor la correlación entre el grado de alineación TI/negocio y el nivel de implementación de buenas prácticas de gestión de TI.
Se comprueba que, en el interior de cada componente de la GTI, los aspectos medidos en el cuestionario diseñado ejercen una influencia diferente. Este análisis está basado en la evaluación de las cargas factoriales y fiabilidades de los indicadores dentro de cada componente. La identificación de qué elementos evaluados tiene mayor influencia en los componentes de la GTI permite la definición de importancias relativas en el diseño de indicadores, así como el establecimiento de acciones de mejora priorizadas dentro de cada componente.
En el caso del nivel de organización de TI dentro de la empresa, este aspecto es explicado en mayor medida por el nivel de definición de procesos de gestión de TI. Dicho elemento es evaluado a partir del nivel de madurez de los procesos de GTI, desde su inexistencia como punto más bajo hasta la implementación de los procesos de forma exitosa y la existencia de un sistema de medición del desempeño definido como máximo nivel. En menor medida influyen en el nivel de organización de TI la definición de estructuras y la definición de mecanismos relacionales. De estos dos aspectos ejerce mayor influencia la participación del responsable máximo de TI de la empresa en los consejos de dirección, que la organización de la función de TI y la definición de roles.
El grado de alineación TI/negocio es mayormente explicado en una empresa por el grado de alineación estratégica. Este aspecto es medido a partir de la definición de una estrategia de TI y su alineación a la estrategia empresarial. El grado de alineación social es el aspecto menos relevante. Para explicar la alineación TI/negocio, la comunicación entre el departamento de TI y la dirección de la empresa es el elemento de menor importancia, aún cuando se pueda afirmar que el responsable de TI siempre asiste a los consejos de dirección de la empresa, y participa conjuntamente con la dirección en la toma de decisiones estratégicas. Se detecta que tiene mayor influencia en el grado de alineación TI/negocio, el nivel en que la disponibilidad de recursos de TI con que cuenta la empresa esté en correspondencia con sus necesidades del negocio.
El nivel de gestión de riesgos de TI en la empresa es el componente de la GTI mejor reflejado por los aspectos incluidos en el cuestionario. Cada elemento que lo conforma ejerce una alta influencia en su comportamiento. En mayor medida influye el nivel de participación de la alta dirección tanto en la identificación de los riesgos como en la evaluación de las estrategias para su disminución. Este aspecto es seguido por el nivel de implementación de prácticas de gestión de riesgos (identificación de los riesgos de TI y el impacto potencial en los objetivos empresariales, planificación de medidas para disminuir los riesgos identificados y administración de riesgos según procedimientos estándares). El aspecto que menos influye es el nivel de percepción de la responsabilidad. No es tan relevante para evaluar el nivel de gestión de riesgos de TI en una empresa si este es un tema que no se limita al responsable de Seguridad Informática.
Con relación al nivel de implementación de buenas prácticas de GTI en la empresa, la cuestión de menor importancia fue el nivel de implementación de estándares internacionales. Este elemento es de hecho el de menor influencia dentro del modelo. Dicho resultado sugiere que, aunque resulta indiscutible teóricamente que la aplicación de estándares internacionales es relevante para elevar las buenas prácticas de GTI en una empresa. Pudiera ser prudente subdividir un elemento tan global en prácticas más específicas que reflejen hasta qué punto se aplican las buenas prácticas abordadas en los estándares. Mayores influencias ejercen las dos restantes prácticas específicas que se incluyeron en el cuestionario. El nivel de implementación del monitoreo del desempeño de TI y su contribución a los objetivos empresariales, medido a partir del empleo de indicadores; estuvo seguido por la evaluación de proyectos de inversión.
V. CONCLUSIONES
Se validó el modelo planteado a partir de que se cumplieron satisfactoriamente las condiciones necesarias para aplicar el AFC; siendo así posible comprobar las interrelaciones entre los componentes de la GTI.
La evaluación mediante cada uno de los índices de bondad de ajuste, avaló tanto la calidad como el ajuste del modelo para con los datos recolectados mediante el cuestionario y se determinó que las estimaciones realizadas son válidas para interpretar el fenómeno teórico representado.
Se comprobó que todas las interrelaciones planteadas son significativas y el componente más destacado es la organización de TI al reflejar las dos interrelaciones más significativas: con el grado de alineación TI/negocio y el nivel de implementación de buenas prácticas de gestión de TI y también la menos significativa con: el nivel de gestión de riesgos.