I. INTRODUCCIÓN
La minería del cobre en Chile constituye el principal sector de atracción de la inversión extranjera; en el año 2018, la industria cuprífera chilena produjo el 27,5% del total de producción mundial, manteniéndose como el mayor productor de este mineral [1; 2]. Las faenas mineras dedicadas a la extracción de cobre en Chile se ubican mayoritariamente en la zona norte, superando el 75% de la producción nacional [3], y siendo las regiones de Antofagasta (II región) y Tarapacá (I región) las que albergan la mayor cantidad de faenas . Donde destacan empreses tales como: compañía minera Escondida, que lidera la producción a nivel mundial; y compañía minera doña Ines de Collahuasi, la cual es una de las 10 empresas privadas con mayor índice de productividad laboral [4; 5].
Debido al gran impacto de sus operaciones, las faenas mineras se ven cada vez más obligadas a optimizar los procesos y operación de los equipos [6], la cual lo han desarrollado mediante la subcontratación de servicios. Según el anuario de la minería de Chile del año 2018, se utilizó 419.000.000 horas personas para el desarrollo de las actividades productivas mineras, de las cuales 67,5% fueron desarrolladas por empresas contratistas o subcontratadas [7]. Por lo cual, queda en evidencia que la subcontratación juega un rol importante en la industria minera chilena.
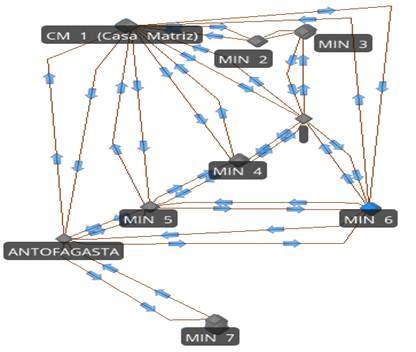
La empresa en estudio es una prestadora de servicios de mantención de equipos mineros, la cual tiene su centro de operaciones en la ciudad de Alto Hospicio, región de Tarapacá. Esta empresa lleva a cabo sus operaciones en 9 faenas mineras y en su casa matriz; todas éstas se encuentran distribuidas entre las regiones de Tarapacá y Antofagasta. Para llevar a cabo sus servicios, la empresa cuenta con un equipo de trabajadores de especialidad mecánica, los cuales deben trasladarse a las distintas faenas durante su jornada laboral para desarrollar sus trabajos cuando son requeridos por las mandantes. Un ejemplo de los trayectos que debe realizar un trabajador para desarrollar sus servicios es representado en Figura 1. El trayecto realizado entre la 1ra y 2da región por un trabajador para atender 3 Órdenes de Trabajo (OT´s) es: Casa Matriz 1 (CM1), Minera 7 (MIN7) y Minera 2 (MIN2), para retornar después a CM 1. En figura 1 se puede observar el movimiento del trabajador entre los clientes, lo cual implica 13.93 horas de traslado, generando en este caso, una espera promedio para la prestación de servicio de 4,64 horas por equipo y una utilización del 30,95% de una jornada laboral corriente de 45 horas.
Debido a lo expuesto anteriormente, es que en este trabajo de investigación se plantea el desarrollo de una propuesta de planeación de personal que permita reducir los tiempos de respuesta de los servicios requeridos por los mandantes mediante la simulación de sistemas.
La simulación de eventos discretos es una de las técnicas más utilizadas en la Investigación de Operaciones y las Ciencias de la Administración [8]. Según Bosijil & Tomicic-Pupek (2017), los procesos de transporte, almacenamiento y manufactura son los tópicos que más se abordan [9], y en concordancia con esto, Trigueiro de Souza et. al (2019), incluye a la logística, la planificación y control de inventarios [10]. La mayoría de los investigadores destacan el uso de la simulación por su habilidad para considerar la variabilidad y las interdependencias, así como su capacidad de proponer diversas soluciones de manera rápida y sencilla mediante pruebas que no interrumpen los procesos productivos [11].
Se pueden encontrar en la literatura casos de estudios realizados con un enfoque de mejoramiento de procesos logísticos. Tal es el ejemplo de Ceballos, Betancur & Betancur (2014) que aplican los modelos de simulación de eventos discretos para reducir las colas en el sistema mediante el análisis de recursos humanos [12]; Gómez, Quintana & Orlando (2015) aplican modelos de simulación al mejoramiento de procesos constructivos [13]. Ambos trabajos, dentro de sus metodologías, recurren al tratamiento estadístico de datos reales para su posterior utilización como información de entrada durante la construcción del modelo. Por otra parte, para una mejor abstracción del mundo real, el uso de software de simulación discreta ha sido utilizado en variadas investigaciones [14]. En el trabajo de Costa & Castaño (2015) se utilizó el software de simulación ProModel para apoyar la toma de decisiones en operaciones logísticas en una empresa de distribución de bienes y servicios de almacenamiento, calculando el punto óptimo de camiones de transporte, maximizando el servicio al cliente [15]. Los autores Achkara, Picechb y Méndez (2015) utilizaron un software de simulación para analizar la gestión logística de materiales vinculados a una línea de envasado de latas, logrando predecir la futura expansión en la capacidad de producción de la empresa. Esta última herramienta de simulación, debido a su flexibilidad y robustez, será utilizada en el desarrollo del presente trabajo [16].
II. MÉTODOS
Para el presente estudio se utilizó una adecuación propia de la metodología de Urquía y Villalba (2013) [17]:
Etapa 1. Definición del sistema
La empresa en estudio lleva a cabo diferentes tipos de servicios como: mantenimientos preventivos y correctivos, habilitaciones de equipos, traslados de maquinarias y equipos, mejoramiento mayor a equipos y máquinas, entre otros.
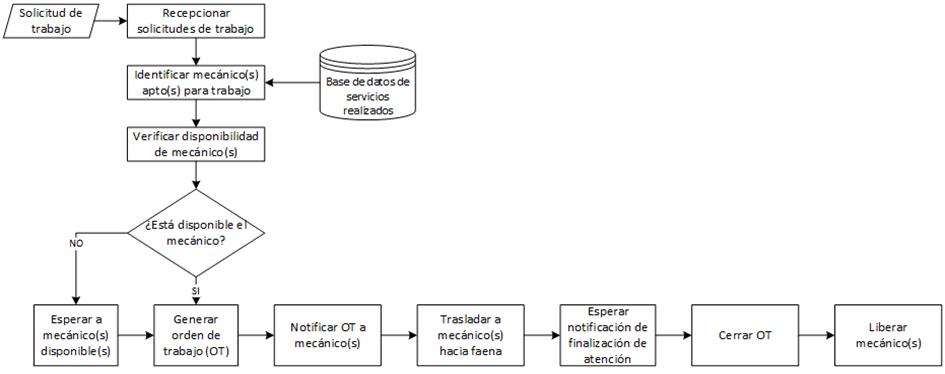
Dependiendo de la complejidad de los servicios, éstos pueden ser llevados a cabo por 1 o 2 mecánicos, los cuales tienen dos tipos de jornadas laborales establecidas. El proceso de servicio comienza con la recepción de la solicitud de trabajo, y la verificación de la disponibilidad de mecánicos. Si se encuentra disponible el personal para la atención del equipo, se genera la orden de trabajo y se notifica al mecánico los detalles del trabajo a realizar. De lo contrario, se debe esperar a que algún trabajador esté disponible. Una vez asignada y notificada la OT, el mecánico debe ir al lugar donde será desarrollado el servicio. Al finalizar su labor, el mecánico debe cerrar la OT dando por terminado el servicio y quedando disponible para otro trabajo, como muestra la figura 2.
Una gran cantidad de OT´s (1239) registró la empresa durante el período 2017-2018, por lo cual se analizaron los servicios que tuvieran mayor demanda. Para esto se aplicó el principio de Pareto [18] el cual arrojó que 32 servicios en 7 distintos lugares de trabajo (6 faenas y casa matriz) constituyen 999 OT´s, como se muestra en tabla 1. La data utilizada fue obtenida mediante sistema interno de la empresa.
Etapa 2. Formulación conceptual del modelo
Los mecánicos cuentan con dos sistemas de jornadas laborales. Por un lado, está el turno laboral 5x2, el cual considera jornadas de lunes a viernes con un máximo de 12 horas diarias y 45 horas semanales. Se dice que este horario es “flexible” ya que el mecánico puede ser requerido a cualquier hora del día con tal de no exceder el máximo diario ni semanal. Por otro lado, está la jornada laboral 7x7, la cual considera ciclos de 7 días de trabajo, con turnos de 12 horas diarias, y 7 días de descanso, éstos no necesariamente comienzan los días lunes. Se dice que esta modalidad es “fija” debido a que las horas de trabajo diarias y semanales están preestablecidas, y los mecánicos con este turno sólo trabajan en una faena específica.
Debido a la complejidad que presenta la modalidad “flexible”, se construyó una secuencia lógica para controlar este tipo de horario. Para la implementación de este proceso se hizo necesario establecer 3 variables para cada mecánico:
una que almacenara las horas trabajadas diarias (horas_dia)
otra que calculara las horas trabajadas semanales (horas_semana)
una tercera que controlara si el mecánico está llevando a cabo un servicio (trabajador_activo).
En la tabla 1 se observan los servicios que representan el 80% de OT´s 2017-2018.
Tabla 1. Servicios que representan el 80% de OT´s 2017-2018
| Número de OT´s | Porcentaje (%) | Porcentaje Acumulado (%) | Número de OT´s | Porcentaje (%) | Porcentaje Acumulado (%) | ||
|---|---|---|---|---|---|---|---|
| 263 | 21,227 | 21,227 | 17 | 1,372 | 67,958 | ||
| 61 | 4,923 | 26,150 | 15 | 1,211 | 69,169 | ||
| 53 | 4,278 | 30,428 | 14 | 1,130 | 70,299 | ||
| 53 | 4,278 | 34,705 | 14 | 1,130 | 71,429 | ||
| 48 | 3,874 | 38,579 | 14 | 1,130 | 72,559 | ||
| 46 | 3,713 | 42,292 | 13 | 1,049 | 73,608 | ||
| 46 | 3,713 | 46,005 | 11 | 0,888 | 74,496 | ||
| 43 | 3,471 | 49,475 | 11 | 0,888 | 75,383 | ||
| 41 | 3,309 | 52,785 | 10 | 0,807 | 76,190 | ||
| 36 | 2,906 | 55,690 | 9 | 0,726 | 76,917 | ||
| 26 | 2,098 | 57,789 | 9 | 0,726 | 77,643 | ||
| 24 | 1,937 | 59,726 | 8 | 0,646 | 78,289 | ||
| 23 | 1,856 | 61,582 | 8 | 0,646 | 78,935 | ||
| 22 | 1,776 | 63,358 | 7 | 0,565 | 79,500 | ||
| 21 | 1,695 | 65,052 | 7 | 0,565 | 80,065 | ||
| 19 | 1,533 | 66,586 | 7 | 0,565 | 80,630 |
El proceso en primer lugar verifica si el trabajador está realizando un servicio (viajando o trabajando en un equipo); en caso de estarlo, se observa si el tiempo trabajado durante la semana supera las 45 horas, en cuyo caso se inhabilita al trabajador para realizar servicios. En caso de no superar las 45 horas semanales, se verifica si el tiempo trabajado durante el día supera las 12 horas, en cuyo caso se le indica al trabajador que descanse 8 horas, tras las cuales volverá a estar habilitado para trabajar y su contador de horas diarias de trabajo se reinicia a 0; si el trabajador no supera las 12 horas de trabajo diarias. Las variables que almacenan el tiempo diario y semanal trabajado se actualizan sumándoles el tiempo trabajado desde la última vez que se realizó este proceso. Este algoritmo debe repetirse con una periodicidad alta (para este estudio se establece como 1 minuto), y su lógica se muestra en la Figura 3.
Al inicio de cada semana las variables 'horas_dias' y 'horas_semanales' deben reiniciarse a 0; por su parte, la variable 'trabajador_activo' se cambia a false si el trabajador termina un servicio, está con actividades suspendidas o está descansando.
Para la atención de equipos, la empresa establece 3 niveles de prioridad que deben cumplirse en el orden en el siguiente orden. El primer nivel de prioridad depende del tipo de servicio, otorgando la primera preferencia a los mantenimientos correctivos, y dejando en segundo lugar a los otros servicios. El segundo nivel de prioridad corresponde al tipo de equipo que requiere atención, siendo el manipulador la primera preferencia, y luego se atienden el resto de los equipos. El tercer nivel de prioridad se organiza acorde a la relevancia que ciertos clientes representan para la empresa (debido a los distintos tipos de contrato y niveles de demanda), siendo la Minera 7 la primera preferencia, luego la Minera 3, la Minera 4, y el resto de las faenas se agrupan como una cuarta preferencia.
Etapa 3. Diseño preliminar de experimentos
Se estableció que los experimentos abordarían 2 aspectos: primero, se modificó la asignación de trabajos y clientes que determinados mecánicos atienden. Por otra parte, se estableció una nueva sucursal desde donde los mecánicos parten a desarrollar los servicios y a la cual vuelven una vez finalizados éstos. Las variables de interés para evaluar los diferentes escenarios fueron 3: el tiempo medio de espera antes de desarrollar el servicio, la distancia total recorrida por los mecánicos, y el porcentaje de utilización total de los mecánicos. Cada experimento simuló un año de actividades de la empresa.
Como límites a los experimentos, se acordó no incurrir ni en contratación ni despido de personal; además de limitar las competencias del personal para realizar determinados servicios a lo reflejado en la base de datos usada para este estudio.
Etapa 4. Preparación de los datos de entrada
En primer lugar, se calcularon las distribuciones probabilísticas para: los tiempos de trabajo de cada servicio, y para el tiempo entre llegadas de cada OT para un equipo y cliente determinados. Una vez que se ordenaron y se seleccionaron los datos a tratar, se ingresaron éstos a un software estadístico con el fin de obtener una curva que represente el comportamiento de los datos. Las distribuciones se obtuvieron mediante la herramienta Input Analyzer de Arena - Rockwell Software, la cual mediante pruebas de error y test de bondad de ajuste entrega la distribución que mejor se ajusta a los datos.
En segundo lugar, se calculó para cada equipo de cada faena la distribución porcentual de las OTs entre los diferentes tipos de servicios prestados por la empresa, así como la proporción de éstas que precisan de 1 y 2 mecánicos para su atención.
Etapa 5. Construcción del modelo
El modelo fue construido en el software SIMIO de simulación [19], el cual tiene un enfoque orientado a objetos y procedimientos para controlar el modelo. En la Figura 4 se pueden ver los objetos que gestionan la creación, procedimiento y despacho de OTs de un equipo (herramienta hidráulica de Minera 7):
'Source' (HIDRAULICA_MIN7), el cual de acuerdo a una distribución de probabilidad genera las OTs.
'Server' (HIDRAULICA_PREV_MIN7_2/ HIDRAULICA_PREV_MIN7/ HIDRAULICA_COR_MIN7_2), el cual recibe la OT y hace los llamados a los mecánicos para que acudan a realizar el trabajo, además de controlar el tiempo que tarda en realizarse el servicio según una distribución de probabilidad determinada. Cada server representa un tipo de servicio y llama a un número determinado de mecánicos.
'Sink' (FIN_TRABAJO), se encarga de eliminar la OT una vez atendida y despachada del Server.
'BasicNode', decide en base a las distribuciones porcentuales calculadas en la etapa 4, qué tipo de servicio solicita el equipo (TIPO_SERVICIO) y cuántos mecánicos precisa para su ejecución (NRO_MECANICOS), de manera que la OT se dirija al Server correspondiente.
Estas redes se construyeron para cada equipo presente en cada faena y fueron agrupadas en el modelo según su ubicación.
El software de simulación empleado cuenta con un tipo de objeto denominado “Worker”, el cual tiene como finalidad simular el comportamiento de trabajadores. A los mecánicos que tienen modalidad de trabajo 7x7 se les asignaron horarios fijos; y para aquellos con modalidad 5x2 se recurrió a la herramienta “Process” la cual ofrece un entorno de programación mediante bloques con instrucciones predefinidas. La posibilidad de utilizar variables creadas y/o existentes para simular comportamientos más complejos, en este último entorno se programó la secuencia lógica presentada en la etapa 2 de este apartado.
Finalmente se construyeron las redes que representan las rutas que siguen los trabajadores de la empresa durante sus operaciones, como muestra la figura 5. Se aprecian las rutas que unen los distintos puntos de interés (ubicaciones de clientes y ciudades), a las cuales se les asignaron las distancias reales mediante revisión de mapas, lo cual permite una representación fidedigna de los tiempos de viaje sin necesidad de construir el modelo a escala. Los trabajadores se mueven en el sistema a una velocidad de 100 km/hr.
Etapa 6. Validación
Las distribuciones obtenidas mediante el análisis estadístico deben pasar por un proceso de validación para verificar que reflejen un comportamiento cercano a la realidad. Si bien existen algunos métodos que son los más reconocidos y usados para la validación de funciones de distribución, en este caso se trabaja con algunos servicios que poseen un número de datos inferior a 10, por lo cual, se procedió a validar estas distribuciones mediante el uso de intervalos de confianza [20; 21; 22].
La aplicación de los intervalos de confianza indica si la media real de los datos se encuentra dentro del intervalo que se elabora a partir de los datos entregados por la función de distribución elegida; si la media está fuera de los límites, debe escogerse otra curva que represente de mejor forma los datos.
La metodología de intervalos de confianza establece que la longitud media (H) de un intervalo de confianza de 100 (1-α) % para la media, basado en la distribución t-student, está dado por la ecuación 1 longitud media intervalo de confianza.:
Donde:
R |
es el número de réplicas. |
S |
es la desviación estándar. |
t |
es el valor correspondiente al 95% en la distribución t-student. |
Con el fin de encontrar un intervalo que cumpla con la precisión deseada, se debe realizar una cantidad mínima de réplicas (R) que permita satisfacer el error (ε) especificado por el analista.
Entonces, un estimado inicial de R está dado por la ecuación 3 Estimado inicial de número de réplicas:
Se toma una muestra inicial R0, ya que de esta manera se puede obtener una estimación de la desviación estándar inicial, y posteriormente se puede calcular la cantidad de réplicas necesarias a simular.
Una vez obtenido el R, se procede a calcular los límites del intervalo de confianza con la ecuación 4 Límites de un intervalo de confianza con distribución t-student:
Posterior al cálculo de los intervalos de confianza, se obtiene el error de cada intervalo con el fin de corroborar que en ningún caso se haya excedido el margen de error definido.
A modo de ejemplo, se expone el proceso de validación para el tiempo de proceso correspondiente al mantenimiento correctivo de manipuladores. En primer lugar, se debe realizar una simulación inicial con R0 réplicas para obtener el estimado inicial de la desviación estándar S0. Se realiza entonces una corrida con 10 réplicas, en cada réplica se atienden 158 equipos, lo cual es igual al número de datos con los que se calculó la distribución del tiempo de este servicio.
La media y la desviación estándar obtenidas de esta muestra fueron
Se utiliza entonces la fórmula para obtener el número de réplicas R necesarias para un error deseado. De esta manera se obtiene que R=13.2374, por lo cual se volvió a correr el modelo con 14 réplicas.
Como producto de esta nueva simulación se obtuvo la media
Etapa 7. Diseño de experimentos
Se creó un escenario inicial contemplando el comportamiento actual del sistema, esto con dos finalidades. Primero, obtener valores de referencia de las variables de interés y segundo, para comparar con los escenarios de mejora propuestos.
Se llevaron a cabo cuatro experimentos con diferentes propuestas de mejora:
En el escenario 1, a 5 mecánicos se les asignó la ubicación ANTOFAGASTA como sucursal de salida, de manera que se evaluase el impacto de asignar parte del personal a una ubicación considerada estratégica por su cercanía a un mayor número de clientes (entre ellos la Minera 7).
En el escenario 2, a los mecánicos se les modificó el número de servicios que éstos atienden, priorizando aquellos con mayor número de OTs en el año y dejando un menor número de mecánicos habilitados para llevar a cabo servicios con poca demanda.
El escenario 3 fue una mezcla de los dos anteriores, asignando parte del personal a ANTOFAGASTA y especializando a los trabajadores para que atendiesen únicamente servicios con alta demanda en faenas cercanas a su sucursal designada.
El escenario 4 fue una variación del escenario 3 al cual se le aplicaron modificaciones según los resultados de este último, especializando de forma aún más marcada a algunos trabajadores.
Respecto del número de iteraciones, se utilizó como base lo ya visto en en la etapa 6, sin embargo, se decidió realizar 550 réplicas para cada escenario propuesto para aumentar la confiabilidad de los resultados y a la vez no comprometer la eficiencia de los recursos tecnológicos y físicos con que se realizó este trabajo [23]. De igual manera permitió encontrar resultados dentro de lo esperado para las 3 variables de interés: tiempo medio de espera de atención, porcentaje de utilización del personal y distancia total recorrida por los trabajadores.
III. RESULTADOS
Se desarrollaron cuatro experimentos enfocados en reducir los tiempos de respuesta de los servicios, y el desempeño de éstos se muestra en la figura 6. Se presentan las medias de los tiempos de espera en horas para cada faena en la situación original y los 4 escenarios simulados (se calculó una media ponderada entre los servicios de cada faena considerando el nivel de demanda de cada una).
La figura representa las variaciones en los tiempos de respuesta fueron leves en CM1 y MIN2. En el caso de MIN7 se produjo una reducción considerable para todos los escenarios.
La segunda variable de interés es la distancia recorrida, cuyos resultados por escenario se muestran en la Figura 7.
El escenario 1 generó una gran reducción en la distancia recorrida (47,12%), y el escenario 2 presentó el único aumento (20,82%).
La tercera variable de interés es el nivel de utilización de los mecánicos. La Figura 8 presenta el porcentaje de uso total respecto a la capacidad actual de la empresa, que es de 43.956 horas hombre.
El escenario 1 mostró la mayor baja en el nivel de uso de mecánicos, y el escenario 2 presentó el único aumento de utilización.
IV. DISCUSIÓN
Escenario 1 presenta la mayor disminución de distancia recorrida en un 47,2%, pero genera un aumento en el tiempo de espera en las faenas CM1, MIN 2 y MIN3; esto se atribuye a que el traslado de mecánicos a la nueva locación en la segunda región genera una menor capacidad de respuesta para solicitudes de clientes en la primera región.
Escenario 2 se observa que la distancia recorrida aumentó en un 20%, y generando una mejora del 9,36% en los tiempos de respuesta para todas las faenas. Se afirma que la especialización del personal tiene un mayor grado de impacto en los tiempos de respuesta, que el establecimiento de una nueva sucursal con mayor cercanía a determinados clientes (aunque esto último implique una disminución en las distancias recorridas).
En escenarios 3 y 4 se aprecia un progreso significativo en los tiempos de espera y la distancia recorrida por los trabajadores, siendo el escenario 4 el que obtuvo mejores resultados en general.
Al comparar los resultados de las Figura 7 y Figura 8, se deduce que la distancia recorrida se relaciona directamente con la utilización de mecánicos. Además, teniendo en cuenta que, a menor utilización mayor es la disponibilidad de trabajo, se afirma que la reducción de la distancia recorrida favorece el aumento de la disponibilidad de los mecánicos.
Considerando que el objetivo del estudio es reducir los tiempos de espera, y teniendo en cuenta la prioridad en algunos clientes, el escenario más adecuado es el 2. Aunque los escenarios 1, 3 y 4, presentan mejores resultados en tiempo de espera; presentan un aumento en el segundo cliente más importante, Faena 3; por lo cual no son considerados como mejores opciones, teniendo en cuanta la prioridad establecida. El escenario 2 es el único que logra una mejora en la calidad de atención en todas las faenas, a pesar de implicar un aumento en las distancias recorridas totales y en el uso de horas hombre.
Se considera que para mantener los buenos resultados obtenidos en el escenario 4 sin aumentar los tiempos de espera en la faena 3, es imprescindible capacitar a los trabajadores con mayor disponibilidad para atender equipos específicos de esta faena
V. CONCLUSIONES
La simulación de sistema, demuestra ser una herramienta válida para la planeación de personal en una empresa de servicio para la minería. Se pudo contemplar las complejidades inherentes de este tipo de empresas como largos tiempos de traslados, variados tipos de horarios laborales, especialización de mano de obra, tiempo de servicios, prioridades de clientes, entre otros.
Los tiempos de traslado de personal tiene un impacto significativo en el aumento de disponibilidad de trabajadores (siempre que el traslado sea parte de la jornada laboral). La reducción de estos tiempos no implica, necesariamente, una disminución en los tiempos de respuesta para el desarrollo de los servicios para todos los clientes, ya que las decisiones al respecto deben adecuarse a las necesidades de la organización bajo estudio.
La especialización del personal tiene un impacto mayor en el tiempo de respuesta para la prestación del servicio comparado con desarrollar nodos cercanos a faenas para la reducción de tiempos de traslado de personal.
Limitaciones de este trabajo de investigación estuvo centrado en la no consideración de los costos asociados en los escenarios desarrollados. Por lo cual se sugiere contemplarlos en futuros estudios, para enriquecer la simulación de sistemas como una herramienta para la toma de decisiones en planeación de personal.