Artículo original

Optimización del deshidratado en cítricos mediante el proceso de secado indirecto al vacío

Optimization of the dehydration in citrus trees through the indirect vacuum drying process

0000-0002-6327-4522Elington Raúl Vélez-Mera^{1  *}  , 0000-0002-6691-0037Neyfe Sablón-Cossío¹  , 0000-0002-1468-615XLenín. J. Pita-Cantos¹ 

¹Universidad Técnica de Manabí, Portoviejo, Ecuador

RESUMEN

El objetivo del artículo es sistematizar la optimización del proceso de deshidratación de cítricos mediante el secado indirecto al vacío en Yara Futuro Agrícola S.A con un modelo de Regresión Lineal Múltiple. La optimización numérica se llevó mediante la Metodología de Superficie de Respuesta a través de un diseño experimental, Box-Behnken, con tres factores. Las variables definidas como: controladas (temperatura interna en la cámara de secado, humedad relativa interna y presión de Vacío) y no controladas (condiciones ambientales, temperatura de entrada del cítrico, humedad de fruta y geometría de la cámara de secado). Como resultado, las pruebas Análisis de Varianza (ANOVA) revelaron que los efectos principales lineales y cuadráticos de estas variables de proceso fueron altamente significativos en la reducción del tiempo de secado. A partir de los resultados de las pruebas estadísticas se ajustó el modelo de regresión de segundo orden, con el cual se obtuvo la configuración paramétrica óptima de los variables.

Palabras-clave: optimización; Box-Behnken; secado; cítricos

ABSTRACT

The objective of the article is to systematize the optimization of the citrus dehydration process by indirect vacuum drying process by Yara Futuro Agrícola S.A with a Multiple Linear Regression model. The numerical optimization was carried out using the Response Surface Methodology through an experimental design, Box-Behnken, with three factors. The variables defined as: controlled (internal temperature in the drying chamber, internal relative humidity and Vacuum pressure) and not controlled (environmental conditions, citrus inlet temperature, fruit humidity and geometry of the drying chamber). As a result, ANOVA tests revealed that the linear and quadratic main effects of these process variables were highly significant in reducing the drying time. From the results of the statistical tests, the second order regression model was adjusted, with which the optimal parametric configuration of the variables was obtained.

Key words: optimization; Box-Behnken; drying; citrus

I. Introducción

El secado de productos agrícolas para su posterior almacenamiento y conservación resulta primordial cuando no se dispone de energía barata para lograr el cometido ^[1]. Debido a esto, a lo largo del tiempo se implementaron tecnologías de procesos como: enlatados, procesos de congelación y secado a escala industrial, en el mundo. Entre estas tecnologías, el secado es probablemente una de las técnicas más antiguas empleadas para la conservación de productos agroindustriales ^[2]. Debido a esto, surge la necesidad de un cambio tecnológico para un proceso más económico y eficiente e innovar en la presentación de los productos finales con los deshidratados laminados ^[3].

Para el secado de los alimentos es un gran desafío eliminar el agua de la manera más eficiente, con un mejor control de la calidad del producto, un impacto mínimo sobre el medio ambiente y a bajos costos operativos. Por ello, el secado a vacío es especialmente adecuado para productos que son propensos al daño por calor, como: las frutas y verduras ^[4].

En este sentido, la optimización del proceso de secado se convierte en un problema a resolver. Por ello, se evalúa la influencia de las variables termodinámicas como: la temperatura en la cinética de secado, difusividad efectiva y calidad de láminas de frutas, resaltando que el proceso de secado convectivo de láminas de fruta presentó dependencia con la temperatura, puesto que al aumentar la temperatura disminuye el tiempo de secado, concluyendo que la cinética de secado es un método efectivo que permite modelar adecuadamente el proceso de secado bajo distintas condiciones ^[5].

Durante muchos años, se desarrollaron modelos matemáticos de secadores con el objetivo de: comprender su funcionamiento, plantear mejoras de diseño, disminuir el tiempo de secado, mejorar la calidad del producto, elegir las condiciones de secado óptimas para aplicaciones industriales a pequeña escala y controlar su funcionamiento ^[1]. Por lo general, estos modelos se basan en las ecuaciones de transferencia de calor, de masa en el aire desecante y el producto. Los mismos, clasifican en modelos de no equilibrio y modelos logarítmicos de Olaciregui ^[2].

A partir de esto, se identifican los cantones de Chone y Flavio Alfaro de Manabí, Ecuador, como los que contribuyen el 40 % de la producción de cítricos a nivel provincial. De esta el 30 % de la producción se pierde en el año. Una de las soluciones a estos problemas sería una fábrica procesadora de cítricos, para que exista un precio fijo de la fruta ^[6]. Es importante enfatizar que para que emplear una materia prima en la deshidratación de cítricos, se le realiza un tratamiento de maduración de acuerdo a la variedad ^[7]. De igual manera, la materia prima se evalúa mediante un análisis microbiológico por laboratorio acreditado que cumplan con todos los estándares de calidad.

Con el desarrollo de esta nueva tecnología del secado al vacío, este proceso no sólo disminuiría el porcentaje de reproceso, sino que impactaría directamente en la reducción del costo de producción. Esto contribuiría a la mejora de la competitividad de las empresas en un mercado cada vez más exigente. Por lo que, el objetivo de este artículo es sistematizar la optimización del proceso de deshidratación de cítricos mediante el secado indirecto al vacío en Yara Futuro Agrícola S.A con un modelo de Regresión Lineal Múltiple. Esta empresa se ubica en Flavio Alfaro la provincia de Manabí, Ecuador ^[8].

II. Métodos

La investigación se desarrolla a partir del estudio de Pons, Villa, y Chou, 2018 ^[9], y se ajusta en tres etapas.

En la etapa 1 es la definición de variables del experimento. A partir de un análisis documental, se definen las variables que intervienen directamente en el proceso de secado de frutas del método de secado por conducción de calor al vacío. A la vez, se efectúa un análisis de los métodos más comunes de secado en cítricos por conducción de calor al vacío. Esto a partir de las variables termodinámica como: temperatura, humedad interna y presión de vacío.

Se describe la metodología de toma de datos en el desarrollo experimental perteneciente a la misma etapa. El manejo de la guía está determinado en función de tres pasos. En el paso 1, se realizó el registro de los datos más relevantes que permitan la descripción general de la investigación. En este punto se realiza la toma de datos mediante los instrumentos y equipos pertinentes para determinar las propiedades termodinámicas internas. En el paso 2, inicialmente se procede a llenar los datos correspondientes a las mediciones de las propiedades termodinámicas internas y externas; posteriormente se describe el comportamiento de transferencia de calor y masa. El registro de las propiedades termodinámicas internas se determina por las mediciones realizadas. En el paso 3, se realizó un extracto de los datos obtenidos de manera experimental, de las variables como la temperatura, humedad, presión de vacío, para luego realizar un estudio de optimización reduciendo el tamaño de la muestra y el error. Esto enmarca el experimento en:

• Las variables controladas son: la temperatura interior en la cámara de secado, la humedad relativa interior y la presión de vacío.

• Las variables no controladas son: condición ambiental (Temperatura ambiente, humedad relativa en la sala de proceso), la temperatura de entrada del cítrico, humedad de la fruta y geometría de la cámara de secado.

Se toman como datos iniciales para este estudio las características físicas y meteorológicas típicas de la ciudad de Flavio Alfaro cantón de la zona norte de la provincia de Manabí - Ecuador. Esta se ubica en las coordenadas geográficas 0° 30', de latitud S y 79° 45' de longitud W y las características típicas de un secador indirecto al vacío de cítricos.

En la etapa 2, aplicación del experimento. Se analizan experimentalmente las variables termodinámicas y con la exploración de un modelo de segundo orden. Se define la relación entre el tiempo de secado y las variables de proceso, que lo hacen variar de manera significativa. Se empleó la Metodología de Superficies de Respuesta (RSM) con la estrategia experimental de Box-Behnken ^[10, ^11]. Esto para obtener las condiciones de operación que permitan obtener el valor óptimo de la velocidad del secado eficiente.

Box-Behnken es una familia de diseños eficientes para factores con dos o tres niveles que permiten, además, un ajuste con modelos cuadráticos ^[10, ^11]. Se trata de un diseño creativo basado en la construcción de bloques incompletos balanceados. Este diseño se implementó para optimizar el tiempo de secado sobre la temperatura, humedad y presión de vacío. En el análisis de las variables los intervalos fueron ampliados, la presión de vacío de 24 a 28 in Hg y la temperatura de 50 a 80 °C, dado que los porcentajes más altos de velocidad de secado incluyeron los valores límites del intervalo de temperatura y presión de vacío evaluado.

La simulación experimental se realizó manteniendo fijo la materia prima a secar, en este caso un cítrico y cambiando las variables controladas (temperatura, humedad relativa, presión de vacío). Se consideraron tres niveles: alto, medio y bajo, para cada variable, en correspondencia con los rangos de operación del proceso que fueron empleados para efectuar su caracterización energética, los mismos que se pueden observar en la tabla 1.

Tabla 1 Niveles de las variables de control 

Variables de Control	Nivel Bajo (-1)	Nivel Medio (0)	Nivel alto (+1)
Temperatura (°C)	50	65	80
Humedad Relativa (%)	30	35	40
Presión de Vacío (in Hg)	24	26	28

El desarrollo experimental se realizó de acuerdo con una matriz de 15 experimentos utilizando la metodología del diseño Box-Behnken, en orden aleatorio, para evitar un error estadístico en los análisis, debido a la acción de variables no controlables. La adecuación del modelo también se comprobó mediante el Análisis de Varianza (ANOVA) ^[12].

Para estudiar los efectos de las variables controlables del proceso secado indirecto de cítricos al vacío con respecto al tiempo de secado. La ecuación 1 representa el modelo utilizado para analizar las respuestas del diseño experimental como función de los tres variables a ser evaluadas a continuación (X ₁ : temperatura, X ₂ : humedad relativa, X ₃ : Presión de Vacío) sobre la variable de respuesta Y (Tiempo de Secado) fue ajustado el Modelo de Regresión Múltiple codificado siguiente ^[10, ^11]:

[TeX:] Y=β0+β ₁ X ₁ +β ₂ X ₂ +β ₃ X ₃ +β ₄ X ₁ X ₂ +β ₅ X ₁ X ₃ +β ₆ X ₂ X ₃ +β ₇ X ₁ ² +β ₈ X ₂ ² +β ₉ X ₃ ² +∑error (1)

Donde:

Y:	Tiempo de secado
X 1 :	Temperatura
X 2 :	Humedad Relativa
X 3 :	Presión de vacío
β 2 , β 1 y β 3 :	Coeficientes de efecto lineal
β 7 , β 8 y β 9 :	Coeficientes de efecto cuadrático, coeficientes de efecto cuadrático
β 4 , β 5 y β 6 :	Coeficientes para la interacción de factores
∑error:	Error aleatorio

En la Tabla 2 se encuentra una matriz de las condiciones utilizadas para el diseño experimental de Box-Behnken realizado en las variables de control como la temperatura, humedad relativa y presión de vacío en el proceso de secado indirecto al vacío, respecto a la variable de respuesta tiempo de secado, se realizaron 15 réplicas.

Tabla 2 Condiciones utilizadas para el diseño experimental de Box-Behnken 

Corrida	Bloque	Temperatura	Humedad Relativa	Presión de vacío
1	1	-1	-1	0
2	1	1	-1	0
3	1	-1	1	0
4	1	1	1	0
5	1	-1	0	-1
6	1	1	0	-1
7	1	-1	0	1
8	1	1	0	1
9	1	0	-1	-1
10	1	0	1	-1
11	1	0	-1	1
12	1	0	1	1
13	1	0	0	0
14	1	0	0	0
15	1	0	0	0

En la etapa 3, se aplicó la herramienta informática y se interpretaron los resultados. El Análisis Experimental se desarrolló en la técnica de secado indirecto al vacío, tienen importancia en el incremento de la eficiencia en el diseño. Esto con la meta de optimizar el proceso de funcionamiento y producción de la tecnología del secado deshidratados en Yara Futuro Agrícola S.A ^[8].

III. Resultados

El procesamiento experimental se muestra como resultados para cada una de las variables que intervienen en el proceso de secado por conducción de calor al vacío. Luego de la ejecución del diseño experimental Box-Behnken arrojó 15 experimentos en cada una de las variables que intervienen en el secado de frutas^[13].

Luego del procesamiento estadístico, en la tabla 3 muestra las condiciones de cada variable, para el desarrollo de los 15 experimentos a ser analizados.

Tabla 3 Resultados de las corridas experimentales del diseño Box-Behnken 

Experimento	Temperatura °C	Humedad relativa % HR	Presión de vacío (in Hg)	Tiempo de secado Hr
1	50	30	26	7,5
2	80	30	26	6,8
3	50	40	26	7,2
4	80	40	26	6,5
5	50	35	24	7,7
6	80	35	24	7,0
7	50	35	28	6,4
8	80	35	28	5,5
9	65	30	24	7,4
10	65	40	24	7,3
11	65	30	28	5,8
12	65	40	28	5,9
13	65	35	26	6,2
14	65	35	26	6,2
15	65	35	26	6,2

Se observa, tabla 4, que los factores principales como la temperatura y presión de vacío son significativa con un nivel de confianza del 95 % (ρ<0.05) El modelo ajustado presenta un coeficiente de correlación R ² = 94.06 % significativo. Mientras tanto el efecto principal de primer orden de la variable humedad relativa, no ejercen una influencia significativa sobre el comportamiento del tiempo de secado.

Tabla 4 Análisis de varianza para el tiempo de secado 

Fuente	GL	SC Ajuste.	MC Ajuste.	Valor F	Valor p
Modelo	9	6,91933	0,76881	25,63	0,001
Lineal	3	6,27000	2,09000	69,67	0,000
Temperatura	1	1,44500	1,44500	48,17	0,001
Humedad Relativa	1	0,02000	0,02000	0,67	0,451
Presión De Vacío	1	4,80500	4,80500	160,17	0,000
Cuadrado	3	0,62933	0,20978	6,99	0,031
Temperatura*Temperatura	1	0,33231	0,33231	11,08	0,021
Humedad Relativa*Humedad Relativa	1	0,33231	0,33231	11,08	0,021
Presión de vacío*Presión de vacío	1	0,03692	0,03692	1,23	0,318
Interacción de 2 Factores	3	0,02000	0,00667	0,22	0,877
Temperatura*Humedad Relativa	1	0,01000	0,01000	0,33	0,589
Temperatura*Presión de vacío	1	0,00000	0,00000	0,00	1,000
Humedad Relativa*Presión de vacío	1	0,01000	0,01000	0,33	0,589
Error	5	0,15000	0,03000
Falta de ajuste	3	0,15000	0,05000	*	*
Error puro	2	0,00000	0,00000
Total	14	7,06933

R ² = 97.88% R ² (ajustado) = 94.06%

Sin embargo, resultó contradictorio que el efecto principal de primer orden de la variable humedad no fuera significativo, aunque el p-valor es cercano al nivel de significación, porque al aumentar la humedad relativa se debe esperar un aumento de la velocidad de secado en cítricos. En la teoría y la práctica del diseño de experimentos, cuando se presentan estas situaciones, entre otras alternativas, se recomienda eliminar aquellos efectos que no sean significativos para aumentar los grados de libertad de la varianza del error ^[14].

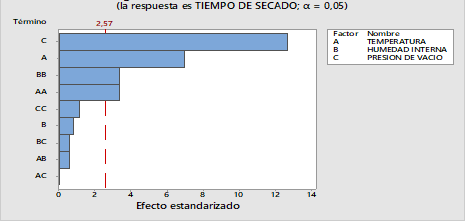
Se realizó el diagrama Pareto de efectos estandarizados, que se observan en la figura 1, [15, 16] , para estudiar de una manera gráfica se analiza la variación de las varianzas sobre el comportamiento de cada una de las variables y sus interacciones, tabla 4. Resultó que el efecto principal de primer orden de la variable humedad relativa y algunas interacciones de segundo orden de las variables controlables, no ejercen una influencia significativa sobre el comportamiento del tiempo de secado.

Fig. 1 Diagrama de Pareto (Efecto Estandarizados) 

Esto condujo a realizar un mejor análisis de varianza denominado ANOVA. Se observa que los efectos principales lineales, incluido el de la humedad relativa, así como los efectos principales cuadráticos de las variables controlables son significativos (p< 0.05). El modelo ajustado presenta un coeficiente de correlación R2 ajustado = 98, 17 %, significativamente mayor al obtenido en el modelo anterior Estos afectan de manera significativa el comportamiento del tiempo de secado en el procesamiento de cítricos, como se refleja en la tabla 5.

Tabla 5 Análisis de Varianza para tiempo de Secado 

Fuente	GL	SC Ajust.	MC Ajust.	Valor F	Valor p
Modelo	5	6,47869	1,29574	150,85	0,000
Lineal	3	5,37500	1,79167	208,58	0,000
Temperatura	1	1,12500	1,12500	130,97	0,000
Humedad relativa	1	0,04500	0,04500	5,24	0,048
Presión de vacío	1	4,20500	4,20500	489,54	0,000
Cuadrado	2	1,10369	0,55185	64,24	0,000
Temperatura*temperatura	1	0,66484	0,66484	77,40	0,000
Humedad relativa*humedad relativa	1	0,51698	0,51698	60,19	0,000
Error	9	0,07731	0,00859
Falta de ajuste	7	0,07731	0,01104	*	*
Error puro	2	0,00000	0,00000
Total	14	6,55600

R ² = 98.82% R ² (ajustado) = 98.17%

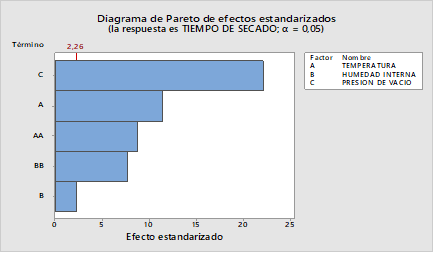
Con el fin de evaluar cada factor y su interacción, se calcula la probabilidad normal de los efectos estandarizados para el tiempo de secado. El diagrama de Pareto de la Figura 2 confirma los resultados del análisis de varianza. El modelo cuadrático no presentó falta de ajuste, por tanto, es adecuado para predecir futuros valores del tiempo de secado.

Fig. 2 Diagrama de Pareto de los efectos estandarizados con p = 0, 05. 

Esta gráfica puede dividirse en dos regiones, la región debajo del 50 %, donde los factores presentan coeficientes negativos (C, T) y la región sobre el 50 % donde los factores y sus interacciones presentan coeficientes positivos (B, BB, TT). Los factores e interacciones que se encuentran alejados de la línea son significativos, mientras que los factores e interacciones sobre la línea, corresponden a un estimado de los errores de los efectos, siendo no significativos. Los valores positivos de los efectos indican que un incremento en sus niveles conlleva a un incremento en el porcentaje de tiempo de secado. Por el contrario, los valores negativos de los efectos, conducen a una disminución de la respuesta (tiempo de secado), cuando sus niveles son aumentados.

De igual forma, en el diagrama de Pareto, Figura 2, se representan los efectos estandarizados con p = 0,05. Se observa que los factores C, y A son los más significativos con igual efecto al observado en la gráfica 2 A. La longitud de las barras corresponde al valor absoluto del efecto estandarizado.

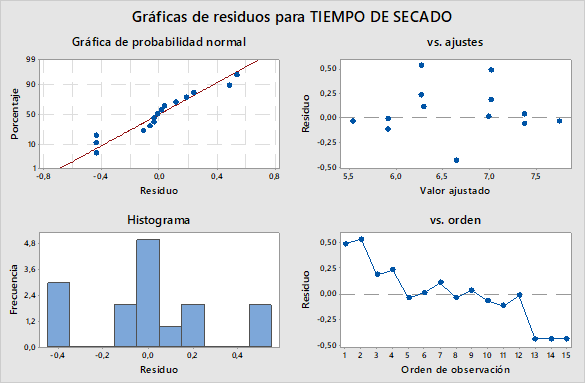
Se comprueba los supuestos de normalidad para la validación del modelo, Figura 3. En esta demuestra que los supuestos de normalidad se cumplen. En base a los residuos se evidencia que no se aprecian violaciones de estos supuestos.

Fig. 3 Probabilidad normal de Residuos 

El tiempo de secado en el proceso de un cítrico se ajusta a la ecuación 2 arrojada por el diseño estadístico. Utilizando este modelo, se puede alcanzar el tiempo mínimo de secado de 5.40 h, bajo las condiciones analizadas, con una temperatura T = 71.5°C, una humedad relativa = 35.45 % Hr y una presión de vacío = 28 in Hg.

(2)

En donde los valores de las variables están especificados en sus unidades originales. La anterior ecuación es válida para T en el intervalo 50-80 °C, Hr entre 30-40 % y Pv. entre 24−28 in Hg, a una temperatura ambiente de 27°C.

Este modelo se utilizó para estimar los valores esperados del tiempo de secado y la combinación de valores de las variables controlables. Con el objetivo de optimizar el proceso de secado en cítricos con respecto al secado tradicional.

En la tabla 6 de refleja rangos de variables controladas a optimizar tabla 7. En base a la optimización del tiempo de secado se tiene en cuenta la combinación de valores de las variables como: la temperatura, humedad relativa en el secador y presión de vacío interna; esto se observa en la tabla 8. Estos hacen mínimo el valor del tiempo de secado en el procesamiento en cítricos de la Empresa Yara Futuro Agrícola S.A, tabla 9. El objetivo es minimizar el tiempo de proceso en el secado. La optimización en la variable de respuesta es el tiempo de Secado.

Tabla 6 Rangos de variables controladas a Optimizar 

Variable	Valores
Temperatura (°C)	( 50; 80 )
Humedad Relativa(%Hr)	( 30; 40 )
Presión De Vacío ( in Hg)	( 24; 28 )

Tabla 7 Parámetros de Variables controladas para la Optimización 

Respuesta	Meta	Inferior	Objetivo	Superior	Ponderación	Importancia
Tiempo De Secado (H)	Mínimo		5,5	7,7	1	1

Tabla 8 Valores que Optimizan el Tiempo de Secado 

Variables de control	Nivel bajo [17]	Nivel alto (+1)	Nivel óptimo
Temperatura	50 °C	80°C	71.45°C
Humedad Interna	30%	40%	35.45%
Presión de Vacío	24 in Hg.	28 in Hg	28 in Hg

Tabla 9 Solución de la Optimización Paramétricas de las Variables Controladas 

Solución	Temperatura °C	Humedad Relativa %	Presión de vacío in Hg	Tiempo de secado ajuste ( Hr)	Deseabilidad compuesta
1	71,5152	35,4545	28	5,40359	1

A partir de estos resultados el proceso comenzó a operarse con los siguientes valores: la temperatura con de 71.45 °C, la humedad relativa es de 35.45 % y la presión de vacío es de 28 in Hg.

Se llevaron a cabo experimentos para validar si los valores obtenidos del tiempo de secado, bajo condiciones normales de operación del proceso, no se observó grandes desviaciones respecto al valor óptimo que fue determinado bajo condiciones experimentales. Un conjunto de 15 experimentos de validación llevados a cabo con la configuración óptima produjo resultados que presentaron desviaciones menores que 25 min de cítricos procesados, en relación con el valor óptimo. Se logró una reducción promedio del reproceso equivalente al 25%, en relación con los valores obtenidos antes de la experimentación con los datos recibidos por parte del área de producción utilizando la técnica de secado convencional por flujo de aire caliente. Por lo tanto, la configuración paramétrica que se muestra en la tabla 9, utilizando la tecnología de secado por conducción al vacío, se consideró óptima para procesar cítricos con una mejor eficiencia energética y un índice de reproceso más bajo.

IV. Discusión

En este campo existen investigaciones, como la deshidratación osmótica de láminas de mango Tommy Atkins aplicando Metodología de Superficies de Respuesta [18] que se enfoca en un diseño experimental factorial (diseño 3³). Las variables analizadas por Zapata y Montoya en el 2012 [18] fueron las mismas que las de este artículo; a pesar que se contribuyó en la mejora del análisis estadístico. Esto debido a que en la medición de las variables de temperatura se ampliaron en sus porcentajes de tiempo de secado más bajos e incluyeron los valores límites del intervalo de temperatura evaluado.

Se encontró un trabajo sobre la influencia de la temperatura en: la cinética de secado, difusividad efectiva y calidad de láminas de frutas por Soto (2013) [19]; donde se realizó un diseño experimental optimizado. Otro estudio, que sí aplica el diseño Box-Behnken pero se utiliza para la optimización de la adsorción del colorante azul ácido sobre residuos de flores es el de Jaramillo, Echavarría y Hormaza (2013) [20].

Carhuajulca Campos (2016) investiga la evaluación y optimización de las condiciones de operación, que influyen en la deshidratación osmótica de la fruta confitada de papaya (carica papaya), se centra en las variables influyentes en el tiempo de secado [21]. Este último elemento se tuvo en cuenta en este trabajo.

V. Conclusiones

1. Las principales variables del proceso identificadas como responsables de la variación del tiempo de secado fueron: la temperatura interna en la cámara de secado, la humedad relativa y la presión de vacío en el interior de la cámara. Cada factor se analizó con tres niveles diferentes según la matriz del diseño Box-Behnken. Se estudió la contribución de estos factores usando pruebas ANOVA para estimar sus efectos principales y de interacción. Las pruebas ANOVA revelaron que los efectos principales lineales y cuadráticos de estas variables de proceso fueron altamente significativos en la reducción del tiempo de secado en cítricos.

2. La optimización paramétrica para hacer disminuir el tiempo de secado conservando la calidad del producto final con respecto a metodologías convencionales, el tiempo en el proceso de secado de madera cativo, se realizó mediante la aplicación de la Metodología de Superficies de Respuesta utilizando un diseño de experimentos de Box-Behnken.

3. A partir de los resultados de las pruebas estadísticas anteriores se ajustó un modelo de regresión de segundo orden, con el cual se obtuvo la configuración paramétrica óptima de los variables del proceso.

4. Los experimentos de confirmación realizados permitieron validar los resultados obtenidos durante la investigación experimental, lográndose una reducción promedio del reproceso equivalente al 25%, en relación con los valores obtenidos antes de la experimentación.

5. Esta investigación confirmó cuán útil es el diseño de experimentos en la mejora del desempeño de los procesos, pues con un número limitado de corridas se pudo determinar la manera óptima de operar el proceso, lo cual no fue posible mediante una caracterización energética que exigió tiempo y muchos recursos.

VI. Referencias

1.  Arhuajulca Campos JF. Evaluación y optimización de las condiciones de operación que influyen en la deshidratación osmótica de la fruta confitada de papaya (carica papaya).2016 26 de mayo del 2021. Disponible en: Disponible en: https://hdl.handle.net/20.500.12802/3182 1.

2.  Cedeño JCDe. 30 % de Cítricos se Desperdicia. El Diario [Internet]. 2018 26 de mayo del 2021. Disponible en: Disponible en: https://Www.Eldiario.Ec/Noticias-Manabi-Ecuador/459503-30-De-Citricos-Se-Desperdicia/ 2.

3.  Jaramillo Madrid AC, Echavarría AM, Hormaza A. Diseño Box-Behnken para la optimización de la adsorción del colorante azul ácido sobre residuos de flores. Ingeniería y ciencia. 2013;9(18):75-91. ISSN 1794-9165.

4.  Mealla-Sánchez LE, Morales-Olaciregui JD. Evaluación del comportamiento térmico de secadores solares en régimen pasivo. TecnoLógicas. 2018;21(4):29-44. ISSN 0123-7799.

5.  Miguel-Olivares JL, Meléndez-Pérez R. Efecto del secado a vacío asistido con ultrasonido en la perdida de humedad, color y dureza en cubos de manzana 2016 26 de mayo del 2021. Disponible en: Disponible en: https://ru.dgb.unam.mx/handle/DGB_UNAM/TES01000788236 5.

6.  Montgomery DC. Design and analysis of experiments. Estados Unidos: John wiley & sons; 2017.

7.  Murguía RÁP, del Pino EMVG, Rodríguez RC. Optimización del consumo de energía en un proceso de secado de madera utilizando diseño de experimentos. Revista Espacios. 2018;39(3):1-14. ISSN 0798-1015.

8.  Padilla-Frías KA, Granados-Conde C, Leon-Mendez G, Pineda YA, Torrenegra-Alarcon M. . Evaluación de la influencia de la temperatura en procesos de secado. limentech, Ciencia y Tecnología Alimentaria 2020;16(1):98-100. ISSN 1692-7125

9.  Sepúlveda L, Contreras E, Cerro D, Quintulén L. Technical feasibility of natural antioxidant recovery from the mixture of the inedible fractions of vegetables produced in a wholesale market. CyTA-Journal of Food. 2021;19(1): 418-28. ISSN 1947-6337.

10.  Soto Ramos R. Influencia de la temperatura en la cinética de secado, difusividad efectiva y calidad de láminas de frutas 2013 26 de mayo del 2021. Disponible en: Disponible en: http://repositorio.uncp.edu.pe/handle/UNCP/2674 10.

11.  Tantas GJV, Aldana MDM. Modelación matemática y simulación numérica de no equilibrio de una cámara de secado solar para cacao 2016 26 de mayo del 2021. Disponible en: Disponible en: http://xxiiispes.perusolar.org 11.

12.  Torres J, Alvis A, Gallo L, Acevedo D, Montero P, Castellanos F. Optimization of the deep fat frying process of arepa con huevo using response surface methodology. Revista Chilena de Nutrición. 2018;45(1):50-9. ISSN 0716-7518.

13.  Vanegas Mahecha P, Parra-Coronado A. Designing, constructing and evaluating a dynamic prototype dryer for obtaining rolled dehy-dehydrated fruit pulp. Ingeniería e Investigación. 2011;31(1):163-70. ISSN 0120-5609.

14.  Zapata Montoya JE, Montoya Rodas A. Deshidratación osmótica de láminas de mango cv . Tommy Atkins aplicando metodología de superficies de respuesta. Revista Facultad Nacional de Agronomía Medellín. 2012;65(1):3-16. ISSN 0718-0764

Recibido: 26 de Mayo de 2021; Aprobado: 07 de Julio de 2021

^*Autor para la correspondencia: [e-mail]

Los autores declaran que no hay conflicto de intereses.

Elington Raúl Vélez-Mera: Realizó la aplicación práctica de la investigación en el objeto de estudio, optimización del deshidratado en cítricos mediante el proceso de secado indirecto al vacío. Se parte del estudio teórico de esta problemática. Se define una metodología de estudio y se interpretan los resultados obtenidos.

Neyfe Sablón-Cossío: [e-mail]. Desarrolló una sistematización de los resultados, y realizó el acápite de discusión del artículo. Revisó y actualizó la bibliografía.

Lenin Julio Pita-Cantos: [e-mail]. Calculó e interpretó los resultados de la aplicación. Revisó el documento de forma holística para ver la armonía y la significación del contenido.