Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.14 no.2 La Habana Mayo-ago. 2011
ARTÍCULO ORIGINAL
Papel de la modelación matemática en la formación de los ingenieros
Role of mathematical modeling in the training of engineers
María Lucía Brito-VallinaI, Isidro Alemán-RomeroI, Elena Fraga-GuerraII, José Luís Para-GarcíaIII, Ruth Irene Arias-de TapiaIV
I Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Mecánica. La Habana. Cuba
II Ministerio de Educación Superior. La Habana. Cuba
III Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Eléctrica. La Habana. Cuba
IV Universidad Estatal Amazónica (UEA). Ecuador.
RESUMEN
Existe una enorme brecha entre las habilidades matemáticas que requiere el ingeniero, vinculadas fundamentalmente a las actividades de modelar, interpretar, comunicarse en un lenguaje preciso, etc., y las habilidades que se forman en los cursos de Matemática, que ponen su mayor énfasis en la actividad de resolver ejercicios de cálculo. Son variadas las causas de este fenómeno, que no es exclusivo de Cuba. El conocimiento científico en general, es concebido por las prácticas sociales, y sin embargo se ha considerado en muchas ocasiones el estudio de las matemáticas como el trabajo con conceptos abstractos, es decir alejados de la actividad humana. La modelación matemática de problemas, crea en los estudiantes una capacidad y habilidad necesarias para la solución de posibles problemas prácticos. El presente trabajo tiene como objetivo proponer una estrategia metodológica que posibilite estructurar de modo sistémico el desarrollo de la habilidad de modelar, teniendo en cuenta la clasificación de los principales modelos matemáticos para las ingenierías; según la teoría o técnica utilizada en su elaboración, la naturaleza de los procesos que desarrollan, su estructura matemática y otras, sin obviar por supuesto, el perfil del profesional de estas carreras y las principales categorías didácticas del proceso de enseñanza - aprendizaje.
Palabras claves: matemática, modelación, ingeniería.
ABSTRACT
There is a huge gap between the mathematical skills required by the engineer, primarily related to the activities of modeling, interpreting, communicating in precise language, etc., And skills that form in the courses of Mathematics and listed in the programs study, which put the most emphasis on solving activity calculation exercises. There are several causes of this phenomenon which is not unique to Cuba. Scientific knowledge is generally conceived by social practices, has emerged and evolved from the practical needs of man, and it has held on numerous occasions, the study of mathematics as working with abstract concepts, is say away from human activity. Mathematical modeling of problems from a particular phenomenon creates in students a capacity and skills needed to solve practical problems. This paper aims to propose a methodological strategy that enables systemic structure so developing the ability model, taking into account the classification of the major mathematical models for engineering, according to the theory or technique used in its preparation, the nature of the processes that develop, their mathematical structure and others, not forgetting of course the professional profile these races and the main categories of educational teaching process.
Key words: mathematical, modeling, engineering.
INTRODUCCIÓN
Modelación matemática
Un modelo constituye una representación o abstracción de la realidad. Entre los diferentes tipos de modelos se pueden mencionar los analógicos, físicos, gráficos, esquemáticos y matemáticos.
La modelación matemática es un intento de describir alguna parte del mundo real en términos matemáticos. Modelos matemáticos han sido construidos en todas las ciencias tanto físicas, como biológicas y sociales. Los elementos que lo componen son tomados del cálculo, el álgebra, la geometría y otros campos afines.
Es natural que los modelos matemáticos sean modelos de analogía incompleta, es decir, que reflejan solamente algunas propiedades del objeto modelado. A la vez, los modelos matemáticos se caracterizan por una suficiente generalidad, describiendo una clase completa de objetos o fenómenos. Por otra parte, la creación de modelos matemáticos no requiere significativos gastos materiales y la realización del propio proceso de modelación con ayuda de los modernos medios de cómputo permite efectuarla en un tiempo relativamente pequeño.
En un modelo matemático se establece un conjunto de relaciones (de igualdad y/o de desigualdad) definidas en un conjunto de variables que reflejan la esencia de los fenómenos en el objeto de estudio. Formalmente un modelo matemático M es una estructura, donde R es el conjunto de las relaciones y V el conjunto de las variables.
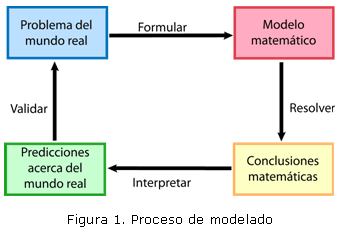
En la siguiente figura 1 se ilustra [1] el proceso de modelado:
Dado un problema del mundo real, la primera tarea es formular un modelo matemático. Para ello se identifican y nombran las variables y se establecen hipótesis que simplifiquen el fenómeno lo suficiente para que pueda tratarse matemáticamente. En lo anterior se pone a prueba el conocimiento de la situación física y las habilidades matemáticas para obtener las relaciones entre las variables. En algunas situaciones en que no se dispone de una ley física, es necesario examinar una colección de datos para reconocer patrones, interpretando los mismos numéricamente, gráficamente e incluso podrían sugerir una representación algebraica.
Papel de la Modelación Matemática en la Formación de los Ingenieros
La segunda etapa es aplicar las técnicas de las matemáticas conocidas al modelo matemático para llegar a conclusiones matemáticas. En la tercera etapa las conclusiones matemáticas se interpretan como información acerca del fenómeno original del mundo real, de manera que ofrezcan explicaciones o se hagan predicciones. El paso final es validar las predicciones al ser comparadas con nuevos datos reales. Si las predicciones no se ajustan bien con la realidad, se redefine el modelo o se formula uno nuevo y se reinicia el ciclo.
Un modelo matemático nunca es una representación completamente exacta de una situación física; es una idealización. En un buen modelo la realidad se simplifica lo suficiente para permitir cálculos matemáticos, pero incluso así es bastante exacto para permitir conclusiones valiosas. Es importante el conocimiento acerca de las limitaciones de un modelo.
De lo anterior se infiere, que para construir un modelo matemático (Deiros Fraga, Beatriz. Optimización Pág. 1 a la 130) es necesario seguir una trayectoria bien definida y desglosada en diferentes pasos adecuadamente ordenados, los cuales constituyen un enfoque lógico y consistente que se denominará estrategia general de la modelación matemática, la cual se basa en el proceso de modelado presentado.
DESARROLLO
La estrategia general de la modelación matemática que aquí se muestra consta de los siguientes pasos:
- Definición del problema y sus objetivos
- Definición de la teoría que gobierna el problema
- Descripción de la situación física en términos matemáticos
- Solución matemática del modelo.
- Comparación del modelo con la situación real.
- Estudio de las limitaciones del modelo.
- Aplicación del modelo e interpretación de los resultados que ofrece.
A continuación se explican los pasos de esta estrategia, aplicándola en un problema ilustrativo:
1. Definición del problema y sus objetivos
La definición de la situación física que se desea modelar debe ser detallada y clara, lo que facilitará la ejecución del resto de los pasos y se garantizará un final exitoso. Además, la modelación matemática, por no ser un fin en sí misma, debe realizarse por necesidad de cumplimentar un objetivo concreto que requiera la manipulación del modelo, por lo que el mismo debe estar claramente establecido.
El problema ilustrativo consiste en estudiar el drenaje de un tanque a través de un orificio situado en el fondo del mismo, el cual al inicio está lleno de líquido.
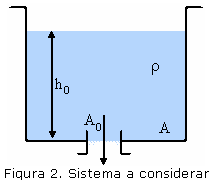
El sistema a considerar tiene las siguientes características:
- El tanque tiene sección transversal constante (A)
- El orificio tiene área conocida (A0)
- La altura inicial de líquido en el tanque es h0
- La temperatura dentro del tanque se mantiene constante, por lo cual la densidad es constante (?).
Se supondrá que el objetivo es obtener una expresión matemática (modelo) que permita conocer cómo varía la altura del líquido en el tanque con el tiempo.
2. Definición de la teoría que gobierna el problema
Se deben identificar las magnitudes importantes o relevantes, decidiendo cuales deben ser despreciadas o ignoradas.
La teoría que gobierna el problema planteado es el principio de conservación de la masa, el cual aplicado a un sistema dinámico establece:
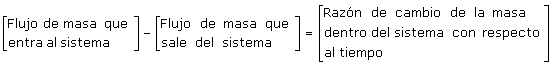
3. Descripción de la situación física en términos matemáticos
Se refiere a la acción de relacionar las variables o parámetros de interés, según la definición del problema y su objetivo, empleando para ello las relaciones matemáticas que ofrece la teoría que gobierna el problema y otras que también puedan ser formuladas e incluso aquellas que el especialista proponga. En este paso debe tenerse en cuenta además el logro del mejor compromiso entre lo riguroso de la descripción del problema y la factibilidad o facilidad de la solución del mismo. En la composición de la descripción matemática del modelo, se distinguen además las ecuaciones de limitaciones en los factores y parámetros del proceso.
El balance de masa planteado en el punto 2 conduce en este caso a la ecuación diferencial:
![]()
donde:
q: Flujo volumétrico de salida del líquido, en m3/s
A: Área del fondo del tanque, en m2
A0: Área del orificio, en m2
h : Altura del líquido en cualquier instante de tiempo, en m
r: Densidad del líquido, kg/m3
t: tiempo, en s.
Como r y A son constantes, entonces
![]()
Se conoce que q es función de h, por lo cual se puede plantear como segunda ecuación del modelo:
q=f(h)
En este caso particular se cuenta con datos experimentales para el tanque en cuestión. Se procederá a establecer distintas alternativas para la relación funcional entre q y h conformando 3 modelos, comparando los resultados de cada uno con el fenómeno real y realizando el análisis comparativo.
Las características del tanque en mm son:
Diámetro: 273
Altura: 305
Diámetro del orificio: 15.5

Estos datos se representan en el siguiente gráfico:
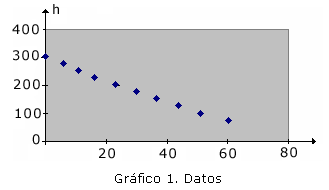
Modelo I
Se asume que no hay dependencia entre q y h, y por lo tanto q=c (constante). Resolviendo la ecuación diferencial y ajustando la condición h(0)=h0, se obtiene el modelo:
![]()
Para valores de t £ 30 se nota que la relación entre h y t es casi lineal, o sea, dentro de este intervalo de tiempo el modelo I explica el comportamiento de la situación física satisfactoriamente.
Modelo II
Se asume una dependencia lineal entre q y h, y por lo tanto q=bh. Resolviendo la ecuación diferencial y ajustando la condición h(0)=h0, se obtiene el modelo:
![]()
Este modelo predice una dependencia exponencial entre h y t; la curva particular será definida por b/a, o sea por el valor del parámetro b, por lo cual se debe buscar el valor de b que dé el mejor ajuste entre el modelo y los datos experimentales, que en este caso se obtiene para b/a=0,0145.
Modelo III
Se asume una dependencia exponencial entre q y h del tipo . Resolviendo la ecuación diferencial y ajustando la condición h(0)=h0, se obtiene el modelo:
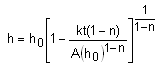
En este tercer modelo hay dos parámetros k y n, los cuales se tienen que determinar a partir de los datos experimentales, con el fin que dé el mejor ajuste entre el modelo y la situación física real. Para este caso se obtienen que n = 0.5 y k = 5.195.
1. Solución matemática del modelo
Raramente la formulación da una respuesta directamente. Usualmente se requiere de una elaboración, para comprobar que la solución matemática de las ecuaciones que lo constituyen es verdaderamente factible, así como dejar claramente establecido los valores de los parámetros necesarios para lograr su solución y el método idóneo a utilizar para ello.
La sucesión de operaciones que es necesario realizar para hallar los valores de las variables y parámetros deseados, se denomina algoritmo.
Por su sencillez, simultáneamente al paso anterior se han solucionado matemáticamente los tres modelos propuestos al evaluar los parámetros en cada uno de ellos.
2. Comparación del modelo con la situación real
Obviamente lo más importante es si las respuestas que da el modelo son correctas, lo que se logra con la comparación de ellas con la realidad. La verificación de la adecuación se realiza comparando los resultados con el sistema real. Teniendo en cuenta que en el paso relativo a la descripción matemática del problema se llegó a un compromiso entre la complejidad real y la simplicidad requerida para manipular posteriormente el modelo, es imprescindible verificar que las simplificaciones o aspectos del problema real ignorados no limitan la validez del modelo. Si la comparación entre el modelo y la realidad física no es adecuada, entonces se procederá a considerar las causas y a realizar las modificaciones que sean necesarias lo que pone en evidencia el carácter cíclico de la estrategia.
Comparando los tres modelos analizados se pueden plantear las siguientes conclusiones:
i. Si el objetivo es encontrar un modelo que explique el comportamiento del tanque en un período de tiempo pequeño, se observará que los tres modelos dan similar dependencia funcional (lineal) entre h y t en este intervalo de tiempo justificándose, en este caso, la utilización del modelo I por ser más simple.
ii. Si el objetivo es encontrar un modelo con propósitos predictivos, el uso del modelo I llevaría a grandes errores sobre todo en problemas donde los cambios de nivel sean una fracción significativa de la altura total, por lo cual sería necesario optar por modelos de mayor complejidad.
iii. Se observa la importancia que tiene la obtención de suficientes datos experimentales y de un buen diseño de experimentos. Por ejemplo, si en este caso se hubieran obtenido datos hasta t=35 s, no se observarían diferencias significativas entre ellos, justificándose la utilización del modelo I.
iv. Se pone en evidencia el papel que debe jugar el ingeniero en la toma de decisiones entre elegir un modelo complejo y obtener una predicción precisa o comprometerse con una menos compleja, pero un modelo más simple. En este caso en particular, como los modelos son relativamente sencillos la decisión no es tan difícil de tomar. En situaciones más complicadas el mejor nivel de compromiso es frecuentemente difícil de alcanzar.
v. Es este ejemplo también se puede observar cómo al comparar el modelo obtenido con los datos experimentales es frecuentemente necesario, para explicar la situación física correctamente, desarrollar un nuevo modelo. En este caso era posible de prever de antemano los resultados obtenidos posteriormente; por ejemplo, el suponer el flujo de salida constante implica que cuando h=0, q=c, lo cual se sabe que no es real, por tanto, era de suponer que el modelo basado en esta suposición fuera solo válido para el período de tiempo inicial donde la variación de la altura con el tiempo fuera una pequeña fracción de la altura inicial total.
Al suponer en el modelo II que q=bh, y obtener una ecuación exponencial, era de esperar que este tampoco explicará la situación física en todo el intervalo de tiempo, ya que de acuerdo con la expresión matemática obtenida se necesitaría un tiempo infinito para vaciar el tanque, lo cual no es cierto en la práctica.
En realidad, el modelo que mejor se ajusta a las condiciones reales es el III. Este resultado era de esperar, ya que de acuerdo con las ecuaciones de Bernoulli se obtiene que ![]() . Puede observarse que esta expresión tiene la misma forma que la supuesta en el modelo III.
. Puede observarse que esta expresión tiene la misma forma que la supuesta en el modelo III.
Lo anterior pone en evidencia que el conocimiento del tratamiento de un problema con condiciones ideales, permite lograr más rápidamente una mejor aproximación a la formulación del mismo. Es frecuente que el ingeniero tenga que desarrollar varios modelos antes de obtener aquel que responda de forma satisfactoria al problema planteado y sus objetivos.
3. Estudio de las limitaciones del modelo
Si la comparación es adecuada, se deben definir las limitaciones que puede tener el modelo para su aplicación posterior incluso por personas ajenas al analista que lo desarrolló. Deben recogerse resumidamente todas las consideraciones hechas en la definición del problema, las agregadas en la descripción matemática y las detectadas en la comprobación del modelo.
Según la selección que se realice atendiendo al análisis anteriormente realizado, es necesario detallar todas las consideraciones que se han tomado respecto a la situación física.
4. Aplicación del modelo e interpretación de los resultados que ofrece
Este paso obviamente constituye el objetivo general de todo el trabajo anterior. Una vez obtenido y comprobado el modelo matemático, el mismo podrá ser utilizado en todas las situaciones que sus limitaciones lo permitan.
El modelo será aplicable en aquellos casos, que cumplen con las consideraciones, que se han tomado respecto a la situación física.
El modelo matemático creado sobre la base de la metodología dada, es un poderoso instrumento para la investigación del objeto estudiado, semejante a un banco de experimentación muy perfecto, y en una serie de casos superior a él. Un banco de experimentación no posee la universalidad y la amplitud de variación de parámetros característicos de la modelación matemático. Este permite variar cualquier parámetro elegido en particular, lo que no siempre es posible en el experimento físico.
Precauciones en la formulación de modelos
Las posibilidades que brinda la modelación matemática son muchas. Por esto, es necesario precisar algunos aspectos vinculados con el desarrollo de los modelos que en unos casos, pueden producir graves errores y, en otros casos, pérdidas de tiempo y esfuerzos innecesarios.
- La primera limitación que incide directamente en la elaboración de un modelo es la relativa a la disponibilidad y exactitud de los datos necesarios para el modelo.
- Se debe determinar con que exactitud se deben conocer los diferentes valores de los parámetros del modelo.
- Otra limitación que presenta la formulación de los modelos matemáticos es la que intrínsecamente está presente en los métodos matemáticos disponibles para su solución.
- Otra precaución muy común es la de atribuirle al modelo cualidades que no llega a poseer.
- Se debe precisar el intervalo de validez del modelo.
Clasificación de los modelos matemáticos
En la medida en que sea capaz de definir el problema bajo estudio de una forma precisa, el modelo que se elabore debe corresponder al comportamiento real. Es por ello que dentro de los principios generales para la construcción de los modelos es primordial el conocimiento con la mayor profundidad posible del problema, así como las implicaciones que tendrán en los aspectos cualitativos y cuantitativos las consideraciones que se realicen en el proceso de construcción del modelo.
Diversas clasificaciones [2, 3] han sido establecidas, tomando en cuenta diferentes aspectos del modelo. Las clasificaciones más útiles, y generalmente, utilizadas en los modelos matemáticos son:
- Según la teoría o técnica básica utilizada en su elaboración
- Según la naturaleza de los procesos que la componen
- Según su estructura matemática
Clasificación de los modelos matemáticos según la teoría o técnica básica utilizada en su elaboración
- Modelos de fenómenos de transporte
- Dentro de estos se plantean todos aquellos modelos basados en los principios físico-químicos que utilizan las ecuaciones fenomenológicas de cambio, es decir, las ecuaciones que describen la conservación de la masa, la energía y el momento
- Modelos de balance de población
- Son los que utilizan los principios de balance de población para la modelación de las características del flujo y el mezclado en determinados sistemas, donde los fenómenos de trans porte no pueden ser planteados o son muy complejos.
- Modelos empíricos
- Se basan en las técnicas de ajuste de datos empíricos estudiados en la estadística.
Clasificación de los modelos matemáticos según la naturaleza de los procesos
De acuerdo con esta clasificación se agrupan los modelos matemáticos en los pares opuestos siguientes:
- Determinísticos-estocásticos
- Los modelos determinísticos son aquellos en los cuales los valores de las variables están especificados de forma precisa para cualquier conjunto de condiciones establecidas, mientras que en el estocástico estos valores no se conocen con exactitud, son inciertos, es decir, son aleatorios o siguen alguna distribución probabilística.
- La industria se caracteriza por numerosas situaciones en que el comportamiento de los factores involucrados es de naturaleza aleatoria o es factible y conveniente tratarla como tal.
- Los modelos estocásticos son más difíciles de trabajar que los determinísticos y requieren conocimiento del cálculo de probabilidades.
- Estacionarios-no estacionarios
- El modelo estacionario considera que no existen variaciones con respecto al tiempo de las diferentes variables y parámetros del sistema.
- Por el contrario, un modelo no estacionario considera variaciones con respecto al tiempo. Estos modelos también se denominan transitorios o dinámicos. Sin dudas es más compleja que la modelación en estado estacionario.
- Parámetro combinado-parámetro distribuido
- En los modelos parámetros combinados se ignoran las variaciones espaciales de las variables dependientes del sistema y de sus parámetros, o sea, el sistema se considera completamente homogéneo. Los modelos de parámetros distribuidos toman en cuenta variaciones en el comportamiento de un punto a otro del sistema. Todos los sistemas son distribuidos, ya que existen variaciones a través de ellos, sin embargo, frecuentemente estas son relativamente pequeñas pudiendo ser ignoradas, y así el sistema puede ser considerado combinado.
- En general, los procedimientos para la solución matemática de los modelos parámetros combinados son más simples que para los de parámetros distribuidos, es por ello que a menudo se aproximan estos últimos al modelo combinado equivalente.
Clasificación de los modelos matemáticos según su estructura matemática
La clasificación que agrupa los modelos de acuerdo con su estructura matemática sirve de guía para conocer la complejidad matemática, y las posibles técnicas de solución en cada caso particular.
En el siguiente esquema se muestra la clasificación basada en la estructura matemática para el caso de modelos determinísticos:
- Ecuaciones algebraicas (lineales, no lineales)
- Ecuaciones diferenciales (ordinarias, parciales)
- Ecuaciones integrales
- Ecuaciones en diferencias (una dimensión, multidimensionales)
Utilizando las clasificaciones dadas anteriormente es posible conocer la descripción matemática más común en el uso de cada tipo de modelo.
La descripción matemática de regimenes estacionarios de trabajo de los modelos con parámetros combinados se realiza mediante ecuaciones algebraicas o trascendentes. Estos modelos no podrían aplicarse en una situación dinámica, pues no sería posible incluir la variación en el tiempo.
Las ecuaciones diferenciales ordinarias se utilizan para la descripción matemática de regímenes no estacionarios de los modelos con parámetros combinados, así como regímenes estacionarios de modelos con parámetros distribuidos, en los cuales los valores de los parámetros solo dependen de una coordenada espacial. En el primer caso, en calidad de variable independiente se utiliza el tiempo; en el segundo, la coordenada espacial. Este tipo de descripción matemática tiene una amplía utilización ya que, el tratamiento matemático no es muy complejo.
Las ecuaciones diferenciales en derivadas parciales pueden tener cualquier número de variables independientes, pero en el casi de análisis de procesos el máximo a utilizar es 4: las tres dimensiones espaciales y el tiempo.
Debido a que en una ecuación diferencial parcial hoy al menos 2 variables y de estas una puede ser el tiempo, tendremos que al menos una variable espacial será variable independiente. Por lo tanto, los modelos que tienen ecuaciones diferenciales parciales son siempre modelos de parámetros distribuidos. Si bien es cierto que los modelos de ecuaciones diferenciales brindan mayores posibilidades de representar más detalladamente el sistema físico real, sus soluciones son de gran complejidad.
Un modelo expresado por ecuaciones diferenciales frecuentemente puede representarse por ecuaciones integrales y viceversa, siempre que esto sea conveniente. Hay métodos para resolver ecuaciones integrales que resultan más sencillos que hallar la solución analítica de la ecuación diferencial equivalente.
El análisis de los objetivos descritos por las ecuaciones diferenciales, en una serie de casos, se sustituye por ecuaciones de diferencias finitas. Para ello, el objeto continuo con parámetros distribuidos se pasa a uno discreto con parámetros combinados, pero que tiene una estructura reticular.
El principal aporte de la clasificación de los modelos matemáticos anterior es servir de guía, brindando elementos acerca de los modelos matemáticos y sus principales características.
Sobre la estrategia para la trabajar la modelación matemática con estudiantes de ingeniería
La importancia de la Matemática en la formación del ingeniero radica en que constituye el lenguaje de modelación, o sea, el soporte simbólico con la ayuda del cual se expresan las leyes que rigen el objeto de trabajo del ingeniero. Por tanto, se debe otorgar prioridad al desarrollo de la capacidad de modelar utilizando los conceptos y el lenguaje de la Matemática, así como a la habilidad de interpretar modelos ya creados sobre la base de los conceptos de la disciplina.
Con la aplicación de métodos de enseñanza - aprendizaje en las diferentes asignaturas que potencien el desarrollo de la habilidad de modelar matemáticamente una situación problémica, se espera propiciar en el estudiante [3]:
- Integración de las matemáticas con otras áreas del conocimiento;
- Interés por las matemáticas frente a su aplicabilidad;
- Mejoría de la aprehensión de los conceptos matemáticos;
- Capacidad para leer, interpretar, formular y resolver situaciones-problema;
- Estimular la creatividad en la formulación y resolución de problemas;
- Habilidad en el uso de la tecnología (calculadora gráfica y computadoras).
- Capacidad para actuar en grupo;
- Orientación para la realización de la investigación;
- Capacidad para la redacción de esa investigación.
Por tanto para favorecer que los estudiantes adquieran las habilidades necesarias en la modelación matemática, se propone como estrategia general en la Disciplina Matemática Superior para las carreras de ingeniería los siguientes aspectos:
- En la elaboración de los programas de la disciplina Matemática para Ingeniería, así como de las asignaturas que la integran, se debe incluir dentro del sistema de contenidos aspectos que impliquen la necesidad de modelar matemáticamente un fenómeno determinado y paralelamente se desarrollen determinadas habilidades en los estudiantes que le permitan captar una visión de su entorno y tomar decisiones adecuadas.
- Proponer a los estudiantes en las diferentes formas organizativas de enseñanza diversos problemas propios de la disciplina Matemática y vinculada con el perfil profesional, teniendo en cuenta los conocimientos adquiridos previamente, que impliquen la necesidad de modelar matemáticamente un fenómeno. El proceso de enseñanza-aprendizaje requiere orientación adecuada, formalización y organización de los contenidos para esto.
- En las clases se debe trabajar la modelación dentro de la enseñanza de las matemáticas (como método para desarrollar el contenido programático), sobre la base de que ya el estudiante se ha apropiado de un sistema de contenidos previos y ha adquirido determinadas habilidades que le permitan enfrentar la solución de un problema que implique modelar un fenómeno e interpretar correctamente su solución.
- Proponer una diversidad de problemas vinculados con la especialidad, donde el estudiante pueda reformar el modelo matemático cuando cambian las condiciones y a partir de los nuevos conocimientos adquiridos.
- Empleo de métodos participativos de enseñanza en el aula, potenciando el componente investigativo en la modelación matemática, propiciando de esta forma el pensamiento crítico e independiente.
- Reformular los instrumentos de evaluación. La prueba escrita y la verificación de si el alumno sabe o no utilizar una técnica de resolución ya no puede ser el único procedimiento. La modelación requiere una evaluación diagnóstica, procesal y de resultados.
Principales ventajas
- Propicia en el alumno una mejor comprensión de los contenidos desarrollados e incrementa el grado de interés del alumno por las matemáticas, debido a la aproximación con el área afín y su aplicación. Permite una mayor seguridad en el profesor para la conducción de la clase, pues puede determinar un tiempo para enseñar el contenido matemático, presentar ejemplos análogos y retornar al modelo director, resolviéndolo y evaluándolo.
- Favorece que el alumno: actúe/haga y no sólo reciba sin comprender el significado de lo que está estudiando: Que investigue, lo que es una actividad poco común a pesar de ser parte del currículo: que cree conocimiento y sentido critico, principalmente en la formulación y validación del modelo; que interactúe y se entere de los trabajos de los demás grupos y compañeros.
- Permite al profesor: estar más atento a las dificultades del alumno. Tomar conocimiento de los trabajos de manera gradual, en especial en el momento en el que orienta a los alumnos, y modificar sus criterios e instrumentos de evaluación.
- Posibilita que los futuros profesionales enfrenten problemas relacionados con su especialidad que potencien una visión de manera crítica, con el propósito de transformar la realidad circundante en aras de su mejoramiento, reforzando el desarrollo de uno de los modos de actuación de los profesionales de hoy en día que es la investigación.
- Potencia la integración de las diferentes estrategias curriculares en la enseñanza de las matemáticas, por cuanto el estudiante necesita del uso de las TIC, el dominio de otro idioma, de la formación medioambiental, de la formación económica, entre otros aspectos, para resolver problemas vinculados con la investigación y obtener soluciones adecuadas.
- Permite que el estudiante enfrente tareas que se le pueden presentar en su futura actividad como profesional.
Principales dificultades
La dificultad principal está centrada en la formación de los profesores y en la falta de vivencia del alumno en un trabajo de esta naturaleza. En la formación de profesores de matemáticas. Por ejemplo, rara vez se da una orientación de modelación ni cómo utilizar este procedimiento en la enseñanza formal. Eso viene ocurriendo más a menudo en esta última década en cursos de formación continua o disciplinas de postgrado en Educación Matemática. Para los alumnos que tuvieron una vivencia de enseñanza en las formas tradicionales, la resistencia a la modelación es significativa ya que este método requiere más empeño en los estudios, requiere la investigación y la interpretación del contexto [4, 5].
Para el profesor:
- Interpretación del contexto.
- En la enseñanza tradicional. Particularmente la de Matemáticas, pocas veces se presentan a los alumnos situaciones problémicas que requieren, después de su lectura e interpretación, una formulación y explicación de ese contexto así como una interpretación correcta y en correspondencia con el problema que se presenta Sin esta vivencia, dentro del proceso de enseñanza - aprendizaje es poco probable que el futuro profesional esté entrenado para enfrentar situaciones que se le pueden presentar en su vida laboral y darle soluciones.
- Referencias bibliográficas.
- Hay pocos trabajos publicados sobre modelación en la enseñanza o trabajos académicos disponibles a los cuales el profesor pueda tener fácil acceso. Sin embargo, en casi todas las áreas hay modelos; matemáticos aplicados (Física, Química Biología Economía, etc.), pero que demandan del profesor una cierta base sobre el área de conocimiento [6].
- Orientación.
- Un curso de perfeccionamiento o un texto sobre el asunto no propicia la confianza suficiente en el profesor para poner en práctica el método de la modelación en un primer momento. Esa confianza. Como también la habilidad. Sólo se adquiere con el tiempo. La orientación de un especialista en el asunto, dirimiendo dificultades y auxiliando en la planificación y conducción de las actividades, propiciaría ciertamente, más confianza en el profesor [7].
- Disponibilidad para aprender y para orientar.
- Para que el profesor pueda orientar al alumno en la realización de sus trabajos, es necesario tomar conciencia de los temas/asuntos por ellos escogidos antes de llegar a la tercera etapa del proceso de modelación como método de investigación, es decir, la delimitación del problema y su planteamiento. Cuanto mayor es el número de grupos de alumnos, mayor es el número de temas y por consiguiente, mayor el tiempo que el profesor tendrá que disponer para estudiar.
Para el alumno:
- Interpretación de un contenido.
- Cuando el alumno es colocado frente a un texto o a un contexto, presenta serias dificultades para leer, entender e interpretar, es decir para hacer una lectura.
- Disponibilidad para investigar.
Los temas exigen investigación, para lo cual, muchas veces, no dispone de recursos. Cabe destacar que cuanto mayor es el tiempo que el alumno dispone para el trabajo, en correspondencia con una orientación adecuada mejor será la calidad del trabajo y del ejercicio de la creatividad.
CONCLUSIONES
El presente trabajo propone una estrategia metodológica sobre la base de la concepción científica más moderna sobre modelación. Esta estrategia posibilita estructurar de modo sistémico el desarrollo de la habilidad de modelar, teniendo en cuenta la clasificación de los principales modelos matemáticos para las ingenierías; según la teoría o técnica utilizada en su elaboración, la naturaleza de los procesos que desarrollan, su estructura matemática y otras, sin obviar por supuesto, el perfil del profesional de estas carreras y las principales categorías didácticas del proceso de enseñanza-aprendizaje.
REFERENCIAS
1. Stewart, J. Cálculo. Trascendentes Tempranas. Cuarta Edición. México: Thomson Learning, 2002. 1191 p. p. 24-48. ISBN: 970-686-127-0.
2. Basmadjian, D. The Art of Modeling in Science and Engineering. Primera edición. Chapman& Hall/CRC, 1999. Capítulos 1-3. 657 p.
ISBN 1-58488-012-0.
3. Biembengut Salett, M., y Hein, N. "Modelación Matemática y los Desafíos para Enseñar Matemática". Educación Matemática. México, DF. 2004.
p. 105-125. vol. 16, nº. 002. ISSN 1665-5826
4. Cámara, V. y Belquis Alaniz, M. N. "Modelación Matemática: su implementación en el aula. Un Desafío para el Docente". En: II REPEM. Santa Rosa, La Pampa, Argentina, agosto 2008. p. 77-79.
5. Ibáñez, J. J. Concepto y Tipo de Modelos Científicos. El Universo Visible Bajo Nuestros Pies. [Consultado el: Mayo de 2008].
Disponible en: http://www.madrimasd.org/blogs/universo/2008/05/10/91441.
6. Martínez Migules, M. "Naturaleza y aplicabilidad de los Modelos Matemáticos". Cuadernos del CENDE, 2003. ISSN 1012-2508.
7. Villa Ochoa, J. A. y Ruíz Vahos, H. M. "Modelación en Educación Matemática: Una Mirada desde los Lineamientos y Estándares Curriculares colombianos". Revista virtual Universidad Católica del Norte. 2009. nº. 27. p. 1- 21. Disponible en: http://revistavirtual.ucn.edu.co/
ISSN 0124-5821.
Recibido: 15 de marzo de 2011
Aceptado: 25 de mayo de 2011
María Lucía Brito-Vallina. Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Mecánica. Cujae.
Correo electrónico: lucy@mecanica.cujae.edu.cu