Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.14 no.3 La Habana sep.-dic. 2011
ARTÍCULO ORIGINAL
Modelo de optimización de parques eólicos
Optimization model for wind farms
Omar Herrera-SánchezI, Antonio Sarmiento-SeraI, Vladimir González-FernándezII, Wolfgang SchellongIII
I Instituto Superior Politécnico José Antonio Echeverría. Centro de Estudio de Tecnologías Energéticas Renovables. CETER. La Habana. Cuba
II Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Mecánica. La Habana. Cuba
III Universidad de Ciencias Aplicadas de Colonia. Alemania
RESUMEN
En la actualidad los modelos de optimización de parques eólicos son de gran utilidad para la industria energética, y el uso de técnicas informáticas resulta una herramienta de fuerza en la búsqueda de las mejores configuraciones de parques eólicos. En este trabajo se describe un modelo de optimización de las configuraciones de parque eólicos, utilizando como criterio la maximización del Valor Actualizado Neto (VAN). Además se presentan algunos elementos complementarios como: funciones de restricciones, filosofía de búsqueda de soluciones y flujo de información dentro del modelo así como un ejemplo de la aplicación del modelo, en una región de Cuba.
Palabras claves: optimización, parques eólicos, modelo.
ABSTRACT
At the present time, the optimization models for wind farms are of great utility for the energy industry, and the use of computer techniques is a strong tool in the search of the best wind farms configurations. In this work an optimization model of the wind farms configuration is described, using as maximize criteria the net present value (NPV). Some complementary elements are also presented as: restriction functions, of search philosophy of solutions and information flow inside the model. Finally an application example of the model is shown, for a region of Cuba.
Key words: optimization, wind farms, model.
INTRODUCCIÓN
El primer trabajo publicado fue el de Mosetti et al [1] el cual aborda el problema de la optimización de la disposición o emplazamiento de los aerogeneradores en un parque eólico.
Su trabajo presenta un novedoso enfoque del problema en grandes parques eólicos, en el que se optimiza la distribución de las turbinas eólicas en un emplazamiento dado para conseguir la máxima extracción de energía con los mínimos costos de instalación posibles.
En el 2004 Norman y Ozkurt [2], publican un segundo trabajo sobre optimización del emplazamiento de las turbinas en un parque eólico. Utilizan el mismo modelo de costos del parque eólico que Mosetti et al. [1]. Aunque su función objeto es ligeramente diferente, coincide con Mosetti et al. [1], en la conveniencia de discretizar el terreno.
En el año 2005 se publican dos trabajos de relevancia en la optimización de parques eólicos. El trabajo de Grady y Hussaini [3] y el de Donovan [4]. El trabajo de Grady y Hussaini presenta al igual que los trabajos anteriores: la utilización de métodos heurísticos de optimización con funciones objetivo muy similares, así como los modelos de debilitamiento del viento debido al efecto de las estelas y modelos de costos del parque eólico. En el trabajo de Donovan [4], se utilizó el método de GVP (General Vertex Packing Problem) [5], para lograr la conexión entre los vértices de la malla ortogonal. La principal diferencia de este trabajo es el empleo del método SIMPLEX para optimizar la configuración del parque eólico.
Del año 2006 hasta la actualidad solamente el grupo de autores Mora et al [6-9] realizó trabajos de optimización de parques eólicos con relevancia, tanto en sus resultados como en su idea renovadora. En el 2007 Mora y González [6] plantean un modelo de planeación y optimización de parques eólicos utilizando una vez más el algoritmo genético cuyo objetivo principal es maximizar el valor actual neto (VAN) de la planta eólica determinado como: la suma de flujos de caja actualizados menos la inversión inicial. El modelo de Mora y González ha sido publicado manteniendo las mismas bases en [7-9].
El modelo presentado en este documento ha sido desarrollado con el objetivo de buscar la configuración de un parque eólico que maximice su VAN o sea, maximizar las ganancias totales del proyecto de parque eólico. Esta tarea se realiza en un dominio definido el cual responde al grupo de vértices que describen el terreno ,incorporando de esta forma la idea de Donovan [4] tras la utilización del GVP (Paquete generalizado de vértices) [5]. Tambien se lleva a cabo la optimización tomando en cuenta una serie de funciones de restricción de las cuales responden a las condiciones de seguridad del parque.
En el caso de estudio se demuestra utilizando una porción de la zona de Gibara, en la provincia de Holguín, Cuba, que el modelo es capaz de realizar la optimización deseada maximizando el Valor Actualizado Neto manteniendo el cumplimiento de las funciones de restricción.
MATERIALES Y MÉTODOS
El modelo presentado en esta trabajo está compuesto por sub-modelos de entrada los cuales introducen la información necesaria para que se realice la maximización del VAN. Los sub-modelos de entrada son los siguientes:
- Base de datos de turbinas.
- Evaluación del recurso eólico.
- Análisis económico.
- Aspectos ambientales.
- Zonas desechadas.
A partir de estos sub-modelos y una vez concluido el proceso de maximización del VAN se obtienen las siguientes respuestas:
Turbina eólica recomendada por el modelo.
- La configuración óptima del parque eólico.
- Cantidad de turbinas eólicas.
- Producción energética individual de cada turbina y del parque eólico.
- Valor Actualizado Neto (VAN).
- Índice de turbulencia que afecta a cada turbina eólica.
La evaluación del recursos eólico ofrece la información inicial necesaria para caracterizar cada uno de los vértices los cuales surgen a partir de la superposición del mallado ortogonal sobre el mapa físico del terreno designado. Estos vértices son denotados como (B) y la conexión entre todos y cada uno de ellos responde a la descripción F = BxB descrita en el GVP [5]. La diferencia de la utilización de esta descripción con respecto a Donovan [4] consta en que no existen sub-conjuntos de unión entre vértices sino que cada uno de los vértices que integran el conjunto total está relacionado con el resto, bajo la anterior descripción.
El conjunto de vértices (B) corresponde a una estructura matricial (M) la cual incluye en cada una de sus filas la numeración del vértice correspondiente y en sus columnas la restante información del mismo la cual se describe de la siguiente forma simplificada:
- Coordenadas del vértice(Bi) (xi,yi,zi)
- Valor de producción energética W(Bi) del vértice en cada una de las direcciones de viento Ø.
- Densidad de potencia del punto T(Bi).
- Índice de turbulencia del vértice Ixx(Bi).
- Rugosidad del vértice Rxx(Bi).
El algoritmo propuesto está basado en el método de la búsqueda exhaustiva de las mejores ubicaciones de los aerogeneradores en el terreno a partir de maximizar el valor actualizado neto del parque. El uso del método de búsqueda exhaustiva viene dado por los altos niveles de seguridad que ofrece el mismo para encontrar una solución óptima. Cada vértice ya seleccionado por el modelo, (Bi), enmarca su búsqueda del siguiente vértice (Bj) en cada uno de los vértices que se encuentran en la red, excepto a él mismo.
La función de maximización del VAN global del parque se expresa en el modelo de optimización en la ecuación 1 en unidades monetarias (UM), mientras que la descripción del VAN es representado en la ecuación 2:
En la ecuación 1, se representa por (N) a la cantidad de turbinas que compone el parque. Para lograr la correcta maximización, se ha forzado el modelo a realizar un análisis de retrospectiva temporal, lo cual implica que de forma ficticia se re-calcula el VAN del parque con cada análisis del vértice (Bi).
El valor actualizado neto de la inversión inicial necesaria para la instalación y puesta en servicio del parque eólico VAN(IPE(Bi)), se aplica utilizando una tasa de interés o depreciación anual del dinero, i.
La construcción y puesta en servicio de un parque eólico con una cierta configuración de turbinas (potencia nominal, tipo, altura y localización geográfica) Bi, requiere de una cierta inversión inicial IPE(Bi), y produce año tras año a lo largo de la vida útil (LT) en servicio del parque, unos flujos netos de caja en el que el subíndice k, hace referencia a cada uno de los años de funcionamiento de la instalación mientras que COM(Bi) son los costos asociados a los gastos ordinarios de operación y mantenimiento [9].
En el análisis de la inversión hay que considerar también el costo actualizado asociado a los gastos de desmantelamiento del parque eólico y restitución del terreno CD(Bi) ,una vez agotada su vida útil en producción ,así como el valor residual actualizado asociado a los ingresos por la venta de los activos del parque al final de su vida útil VR(Bi). Tanto el costo actualizado de desmantelamiento de un parque eólico como su valor residual suelen ser pequeños y representar el 1-3 % de la inversión total [9]. Se considera también que E(Bi) es la cantidad neta anual de
energía eléctrica producida y vendida, que pkWh es su precio de venta, DpkWh es su incremento anual y DCOM (Bi) representa el incremento anual de los costos de operación y mantenimiento.
RESULTADOS Y DISCUSIÓN
Restricciones de proximidad y máxima distancia de búsqueda
La primera restricción de distancia responde como factor principal a evitar el choque de las pala entre dos aerogeneradores lo cual queda declarado con la ecuación 3. Comenzando por el vértice en turno (Bi), con coordenadas en la red ortogonal (xi,yi), siendo (b) la mínima distancia para que sea aceptado por el modelo como ''habilitado'' otro vértice (Bj) con coordenadas (xj,yj) . Este es el primer análisis para la exclusión de vértices en el proceso de búsqueda de la mejor configuración del parque.
Para incrementar la eficiencia del proceso se utiliza el código binario en la descripción y detección de cada uno de los estados de disponibilidad en los vértices. En caso de que el vértice (Bj) sea inhabilitado por la restricción de distancia es clasificado con valor 1 y en caso contrario se le atribuye el valor 0.
La segunda restricción de distancia se enmarca en delimitar el área de búsqueda de la solución óptima (ecuación 4), disminuyendo de esta forma el tiempo de corrida del modelo.
La distancia máxima (L) expresa el máximo radio del área de búsqueda del vértice (Bi). Este valor puede ser cambiado por el planificador acorde al tiempo de corrida, a la calidad del microprocesador de la computadora designada a correr el modelo y el nivel de precisión que requiere la respuesta.
Restricciones al incremento del índice de turbulencia. Modelo de estelas
El siguiente paquete de restricciones responde a los valores de índices de turbulencias admisibles por las turbinas eólicas que componen el parque. Estos valores dependen directamente de la Clase y del tipo de turbina eólica [10].
En la dirección aguas abajo de los aerogeneradores, ocurre la estela. En este fenómeno existe una disminución parcial de la velocidad de viento debido a la interferencia de las turbinas en la dirección de flujo, lo cual conlleva a un aumento significativo de la intensidad de la turbulencia [11, 12].
El método empleado por el presente modelo de optimización de parques eólicos para determinar la reducción energética producto al efecto de la estela de los vértices Bi y Bj fue el método de Frandsen [13] modificado por Katic y N. O. Jensen [14] (ecuación 5).
Cuando el flujo libre de viento impacta con la turbina eólica, ocurre una expansión lineal de la estela generada aguas abajo y una porción de la velocidad del flujo libre se reduce de la velocidad original, de ventrada a vsalida del rotor del aerogenerador.
El déficit de velocidad de viento vdef que genera la diferencia entre ventrada y vsalida es la fracción de reducción del flujo libre provocada por la estela. Este valor es calculado mediante la siguiente ecuación:
El valor ![]() de depende de las fuerzas aerodinámicas globales que actúan sobre las palas de los aerogeneradores y están presentes en las curvas de potencia de los mismos. El valor de a es calculado mediante la siguiente expresión empírica:
de depende de las fuerzas aerodinámicas globales que actúan sobre las palas de los aerogeneradores y están presentes en las curvas de potencia de los mismos. El valor de a es calculado mediante la siguiente expresión empírica:
En esta ecuación el valor de (Z) representa la altura del buje del aerogenerador mientras que el valor de Z0 la rugosidad del terreno. El valor de (R) responde al radio del rotor del aerogenerador mientras que la distancia de cada uno de los vértices afectados por la estela aguas debajo desde el aerogenerador en turno está representada por la letra s.
La función ![]() está definida para cada una de las direcciones de interacción inter-aerogeneradores afectando solamente el factor de escala C de la ecuación de distribución de Weibull [15] de la siguiente manera:
está definida para cada una de las direcciones de interacción inter-aerogeneradores afectando solamente el factor de escala C de la ecuación de distribución de Weibull [15] de la siguiente manera:
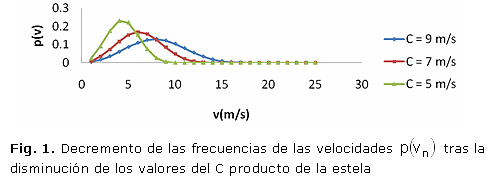
Esta reducción del parámetro C produce una disminución de las frecuencias que corresponden a las velocidades en los vértices afectados por la estela como se aprecia en la siguiente figura 1.
Para un vértice (Bj) a medida que aumenten sus afectaciones por la acción de estelas múltiples debido a la acción de otros vértices (Bi), mayor será la reducción de las velocidades de entrada al mismo y por lo tanto menor será la producción energética total. El valor de la producción energética de la turbina eólica W(Bi,f), en la dirección de viento definida Ø queda reflejado según la expresión 8 en donde P (Vn), la curva de potencia de la turbina eólica p(Vn) la distribución de Weibull, (T) representa el número de horas en las que el instrumento de medición registró alguna velocidad de viento en el sector Ø, ![]() representan las velocidades de viento de salida y entrada respectivamente de generación en la turbina eólica.
representan las velocidades de viento de salida y entrada respectivamente de generación en la turbina eólica.
De esta forma queda definida la producción energética total del aerogenerador E(Bi) en la expresión 9 en donde ft responde al total de sectores de viento con el que se trabajó.
Los valores de C también disminuyen a medida que la distancia aguas abajo inter-aerogeneradores es menor, teniendo de esta forma el valor mínimo inmediatamente a la salida del rotor.
Este decremento de C, ya sea por estelas múltiples, o por distancias inoperantes aguas abajo entre aerogeneradores también puede implicar la reducción considerable de la vida útil de los mismos, debido esencialmente a los grados de turbulencia a los que se someten.
En el presente modelo de optimización de parques eólicos se propone la utilización de la intensidad de la turbulencia como parámetro decisivo en la habilitación o no de un vértice (Bj) en el proceso de optimización y a esto lo rigen dos motivaciones principales:
- Menores daños estructurales en las turbinas aguas abajo.
- Mayor eficiencia en la producción energética de las turbinas.
En la ecuación 10 se describe la intensidad de la turbulencia total (IW) como el incremento sufrido por la turbulencia sin perturbación del vértice (Ixx) debido a la turbulencia adjunta (Iadd)[16].
El análisis de la turbulencia adjunta se determina a partir del método de Frandsen and Thøgersen [17], ecuación 11, en la cual se describe el decremento de la turbulencia adjunta Iadd a medida que aumenta la distancia aguas abajo.
Con la utilización de las ecuaciones de Frandsen and Thøgersen, cada velocidad responde a un valor de turbulencia, por lo tanto la perturbación tendrá más o menos distancia de acuerdo al valor inicial de la velocidad que pasa a través del rotor, tal como se muestra en la figura 2.
El valor para delimitar el inicio de la estela está en dependencia del máximo valor de turbulencia Iw,max
El valor de turbulencia Iw del vértice en cuestión tiene que ser menor que el valor máximo admisible del mismo vértice. Este valor máximo admisible Iw,max responde a la norma IEC 61400-1[10] en la cual este valor responde directamente a la Clase y el tipo de turbina eólica.
Con esta expresión el sub-modelo en cada proceso de búsqueda, realiza una comparación entre las ecuaciones 12 y 10, quedando eliminados los vértices donde Iw < Iw,max .Análisis que se describe en la siguiente figura.
La figura 3 fue elaborada a partir de una velocidad predominante de 5 m/s. El valor de (Ixx) de 0.11 para una rugosidad del terreno de 0.05 m.
El modelo realiza este análisis en todos los sectores de la evaluación de recursos y son señalados en la base de datos del modelo los vértices Bj que se encuentran bajo la influencia de la estela, los vértices que son rechazados y los vértices que están completamente habilitados sin perturbaciones de ningún tipo. Estas restricciones quedan registradas de la siguiente forma:
En la ecuación 13 se determina a partir de la variación de las coordenadas de los vértices Bj y Bi, cuáles son los rangos de distancia admisibles, en cada sector de viento. El valor ![]() es definido como la distancia de rechazo como se manifiesta en la figura 3 y es calculada a partir de las ecuaciones 10, 11 y 12. La ecuación 14 es usada de esta forma porque en ocasiones la rugosidad del terreno cambia fuera de la distancia de rechazo y por lo tanto en ese caso es necesario redefinir la función de restricción 13. Esta restricción evita alguna posibilidad de incluir como válido un vértice con turbulencia peligrosa, sin tener en cuenta en qué área de búsqueda se encuentra.
es definido como la distancia de rechazo como se manifiesta en la figura 3 y es calculada a partir de las ecuaciones 10, 11 y 12. La ecuación 14 es usada de esta forma porque en ocasiones la rugosidad del terreno cambia fuera de la distancia de rechazo y por lo tanto en ese caso es necesario redefinir la función de restricción 13. Esta restricción evita alguna posibilidad de incluir como válido un vértice con turbulencia peligrosa, sin tener en cuenta en qué área de búsqueda se encuentra.
Caso de estudio
La zona de análisis en este caso de estudio fue un terrero de 2.52 km2 del Municipio de Gibara, en la provincia de Holguín, en Cuba.
La resolución del mallado ortogonal superpuesto sobre el terreno de trabajo fue de 60 m y la evaluación del potencial eólico se realizó utilizando el programa profesional para este fin WasP 8.3. El modelo propuesto de optimización de parques eólicos esta programado en plataforma Matlab.
Las cinco turbinas modeladas en este caso de estudio responden a un diámetro de 52 m y una altura de buje de 49 m con 850 kW de potencia. El costo aproximado de este tipo de turbinas, según Fingersh, Hand y Laxson [18] es de 880 328 cuc incluyendo la cimentación. Las demás variables económicas quedan descritas en la tabla 1.
En la figura 4, los vértices circulados con coloración azul representan las turbinas eólicas ubicadas y los vértices negros son los vértices rechazados por alguna de las restricciones. Los vértices verdes representan los afectados energéticamente por la reducción de la ecuación 7 mientras que los vértices rojos representan los no influenciados por la estela
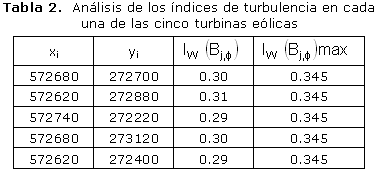
Tras la optimización del parque eólico, el modelo propuesto determinó una configuración en la cual se tiene un VAN de 2 558 000 CUC, produciendo 11.6 GWh, con una eficiencia de la configuración de 94.6 % y un factor de capacidad de un 15.7 %. Como principal ventaja de esta configuración es que, ninguno de los vértices seleccionados por el modelo como turbinas eólicas presentó índices de turbulencia por encima de los valores admisibles como se puede apreciar en la figura 4 y en la tabla 2.
CONCLUSIONES
En el documento se presenta una estructura y parte del algoritmo de un modelo propuesto de optimización de parques eólicos. Este modelo tiene como principal característica la maximización del valor actualizado neto (VAN) como función objeto y la incorporación de los índices de turbulencia como factor principal en la posibilidad de que algún vértice sea rechazado en análisis de optimización.
A partir de esto se elabora una serie de funciones de restricción las cuales tributan a incrementar la aplicabilidad del modelo, tanto por disminución del tiempo de cómputo como por la disminución de un factor de riesgo importante como lo es la turbulencia.
Se expuso un ejemplo de la aplicabilidad del modelo de optimización de parques eólicos en una pequeña porción de Gibara, obteniéndose resultados satisfactorios en todos los aspectos analizados en el documento.
REFERENCIAS
1. Mosetti, G., Poloni, C., et al. "Optimization of wind turbine positioning in large wind farms by means of a genetic algorithm". Journal of Wind Engineering and Industrial Aerodynamics. 1994, vol. 51, p. 16-105. ISSN 0167-6105.
2. Aytun Ozturk, U. y Norman, B. A. "Heuristic methods for wind energy conversion system positioning". Electric Power Systems Research. 2004, vol. 70, p. 179-185. ISSN 0378-7796.
3. Grady, S. A., Hussaini, M. Y., et al. "Placement of wind turbines using genetic algorithms". Renewable Energy. 2005, vol. 30, p. 259-270. ISSN 0960-1481.
4. Donovan, S. "Wind farm optimization". En: 40th Annual ORSNZ Conference. Wellington, New Zealand: Victoria University. 2005.
5. Smith, H. D. "A class of web-facets for the generalized vertex packing problem". Discrete Applied Mathematics. 2005, vol. 146, p. 273-286. ISSN 0166-218X.
6. Castro Mora, J., Calero Baró, J. M., et al. "An evolutive algorithm for wind farm optimal design". Neurocomputing. 2007, vol. 70, p. 2651-2658. ISSN 0925-2312.
7. Castro Mora, J. Optimización global de rarques eólicos mediante algoritmos evolutivos. Sevilla, España: Universidad de Sevilla, 2008. Disponible en: http:// catedrasempresa.esi.us.es/endesared/documentos/ Tesis_Jose_Castro_Mora.pdf
8. Serrano González, J., González Rodríguez, Á. G., et al. "New tool for wind farm optimal design". En: IEEE Bucharest Power Tech Conference Bucharest. Romania: IEEE Power & Energy Society. 2009.
9. Serrano Gonzalez, J., Gonzalez Rodriguez, A. G., et al. "Optimization of wind farm turbines layout using an evolutive algorithm". Renewable Energy. 2010, vol. 30, nº p. 1-11. ISSN 0960-1481.
10. IEC. Standar Turbines. Part 1-Design Requerim. IEC 61400-1. 2005-2008.
11. Emami Alireza, N. P. "New Approach on optimization in placement of wind turbines within wind farm by genetic algorithm". Renewable Energy. 2010, vol. 35, p. 1550-1564. ISSN 0960-1481.
12. Sorensen, J. D., Frandsen, S., et al. "Effective turbulence models and fatigue reliability in wind farms". Probabilistic Engineering Mechanics. 2008, vol. 23, p. 531-538. ISSN 0266-8920.
13. Frandsen, S., Pryor, B. R., et al. "Analytical modelling of wind speed deficit in large offshore wind farms". Wind Energy. 2006, vol. 9, p. 39-53. ISSN 1095-4244.
14. Katic, J. y Jensen, O. "A simple model for cluster efficiency". En: European Wind Energy Association Conference and Exhibition EWEC'86. Rome, Italy: European Wind Energy Association. 7-9 October, 1986.
15. Lackner, M. A. y Elkinton, C. N. "An analytical framework for offshore wind farm layout optimization". Wind Engineering. 2007, vol. 31,
p. 17-31.
16. Vermeera, L. J., Sorensenb, J. N., et al. "Wind turbine wake aerodynamics". Progress in Aerospace Sciences. 2003, vol. 39, p. 467-510.
17. Frandsen, S. "Integrated fatigue loading for wind turbines in wind farms by combining ambient turbulence and wakes". Wind Engineering. 1999, vol. 23, nº 6, p. 327-339. ISSN 0309-524X
18. Fingersh, L., Hand, M., et al. Wind turbine design cost and scaling model. Cole Boulevard, Golden. Colorado: National Renewable Energy Laboratory. Rep. Nº: 200,1617. p. 6-22.
Recibido: 01 de marzo de 2011.
Aceptado: 19 de julio de 2011.
Omar Herrera. Instituto Superior Politécnico José Antonio Echeverría. Centro de Estudio de Tecnologías Energéticas Renovables. CETER. La Habana. Cuba.
Correo electrónico: oherreraz@ceter.cujae.edu.cu













 (UM) (2)
(UM) (2)  (5)
(5) 
 (11)
(11) 
 (12)
(12)